基于CEEMD-排列熵的循环策略信号提取方法*
尹昱东 明 勇 边 羽
(①西安交通大学机械工程学院,陕西 西安 710049;②成都理工大学地球物理学院,四川 成都 610009;③成都开放大学,四川 成都 610051;④内蒙古大学电子信息工程学院,内蒙古 呼和浩特 010000)
目前,非线性科学已迅速发展涵盖到了各个学科领域,其中,尤以混沌时间序列的研究最为突出,占据了很大的比重[1],混沌预测是非线性科学领域的一个热门课题,已经应用到短时交通流、深部岩体变形、风电场短期风速预测、短期电力负荷预测及海杂波中雷达目标信号提取[2]等多个方面,由于混沌时间序列具有较强的非平稳性、突变性等特点,如何建立高精度的逼近混沌系统的预测模型本身就是一项难题,若是实测信号受到噪声的干扰,势必导致混沌预测难上加难,干扰与混沌时间序列本质特征相互耦合和缠绕,掩盖了系统的内在动态特性,这为系统状态分析和参数预测带来了困难,并且混沌信号具极强的似噪声性,其频谱是连续的宽谱,导致混沌信号和噪声会在相同或相近频率段重合,致使传统的线性去噪方法和频谱分析方法难以将其分离[3]。
目前常用的非线性非平稳信号降噪方法是Huang N E等[4]提出的经验模态分解(empirical mode decomposition,EMD)及其相关延伸改进算法,已被广泛应用于多个领域,但尚存在以下问题:①EMD由于异常事件的干扰,使分解得到的固有模态分量(intrinsic mode function,IMF)中含有不同尺度的信号,或是相近尺度信号分布在不同固有模态分量中,即模式混叠,增加了信号重构误差;②总体平均经验模态分解[5](ensemble empirical mode decomposition,EEMD)通过多次叠加和抵消白噪声减小模式混叠,但是EEMD预处理过程耗时过长,时效性差;③EEMD固有模态分量中有用信号的特征提取方法在噪声未知情况下难以取得理想效果[6]。针对以上问题,国内外学者进行了大量研究,文献[7]对输入信号进行B样条最小二乘拟合,改善时间尺度分布,弱化异常事件对信号的影响,达到抑制EMD模态混叠的作用,但是对于信号提取方法的处理方面尚未提及;文献[8]在EMD阈值处理时,根据IMF间功率谱密度关系确定噪声强度,然后采用硬阈值处理方法,忽略了硬阈值带来的不连续性问题;文献[9]在使用EEMD对惯性导航信号降噪时,提出了改进的区间阈值降噪方法,合理设置调节因子能兼顾软硬阈值函数的优势,降噪效果比较依赖于调节因子的选择,并且没有改善EEMD耗时的问题;Yeh J R等[10]在EEMD基础上提出了补充的总体平均经验模态分解方法(complementary ensemble empirical mode decomposition,CEEMD),通过添加相反白噪声抵消信号中的部分噪声,抑制了噪声引起的模态混叠的同时减小EEMD叠加白噪声引起的重构误差;在阈值处理方面,文献[11]利用CEEMD-排列熵确定噪声含量较多的IMF分量,然后采用小波阈值降噪方法对含有较多噪声的IMF分量进行降噪处理以保留有用信息,小波阈值降噪效果较为依赖阈值选取的准确性。
为解决经验模态分解及其延伸算法在信号特征提取存在的问题,在抑制噪声的同时,更好保留有用信号,本文提出了基于CEEMD-排列熵的梯度投影稀疏重构降噪方法,原始信号经CEEMD处理,对信号叠加相反白噪声抑制白噪声引起重构误差的同时简化了计算方法,有效解决了EMD模式混叠和EEMD耗时过长的问题,对分解得到的本征模态分量通过计算排列熵确定噪声分量和信号分量,考虑到信号中噪声先验知识未知,提出了基于奇异值分解的循环策略信号提取方法,利用噪声的排列熵较大这一特性,合理设置奇异值有效重构阶次的选取,该方法无需信号和噪声的先验知识,在抑制噪声的同时,可以较好保留有用信号。
1 算法基本原理
1.1 CEEMD算法
EMD分解是基于以下假设:信号至少有两个极值点:一个最大值和一个最小值;数据的局部时域特性是由极值间隔来确定;若数据缺乏极值但是含有拐点,则可以通过对数据微分一次或多次求取极值点,然后再通过积分获取分解结果。实际采集的振动信号数据较长,在时域范围内含有多个局部极值点,满足上述假设条件,所以EMD已被广泛应用于非线性振动信号处理。实测的振动信号通过EMD筛分过程分解为一系列频率由高到低排列的固有模态分量和一个余项。
CEEMD是在EMD基础上的改进,同时可以有效减小EEMD叠加的白噪声无法完全抵消引起的重构误差及运算时间过长的问题,具体步骤如下:
步骤1:对含噪原始信号叠加一组白噪声序列n1(t),将加噪信号经EMD处理得到一组固有模态分量c1i和余项r1。
步骤3:重复步骤1-2,得到n组cni、rn、c-ni、r-n。
步骤4:对步骤3的多组IMF分量进行平均组合得到分解后最终的IMF。
(1)
(2)
其中:cj(t)表示CEEMD处理最终得到的第j个IMF分量,cni表示信号经EMD处理后得到的n组中的的第j个IMF分量、rn(t)表示CEEMD处理最终得到的余项,ri表示信号经EMD处理后得到的n组中的的第i个余项。
1.2 排列熵
排列熵(permutation entropy, PE)是度量时间序列非逻辑性和复杂度的一种有效方法,PE具有计算简单、抗干扰能力强等优点,对非线性数据具有较强的鲁棒性,其计算方法如下:
对时间序列{x(i),i=1,2,…,N}进行相空间重构
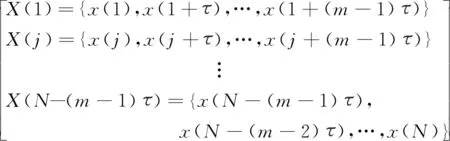
(3)
其中:m为嵌入维数,为时延。
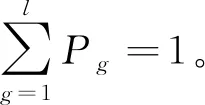
于是,时间序列{x(i),i=1,2,…,N}排列熵以Shannon熵形式表示为:
在记录词集中,词汇可出现的位置有:标题、关键词、成因和答案等,出现在不同的位置对检索结果的贡献值不同,所以其重要性也不同。例如,出现在标题中的词汇的重要性要比出现在答案中的词汇重要。
(4)
在Pg=1/m时,得到Hp(m)的最大值ln(m!),因此,可以通过ln(m!)将Hp(m)进行如下归一化处理:
Hp=Hp(m)/ln(m!)
(5)
Hp在[0,1]之间取值,表示序列的随机程度,并且其值越大,表示序列随机性越强,值越小,则时间序列越规则。
文献[12]列出了噪声和几种常见信号的排列熵,如表1所示,可以看出,噪声的排列熵较大,这与噪声的随机不规则特性吻合,正弦信号、调幅信号以及调幅调频信号等规则性信号的排列熵较小,而间歇性信号相比正弦信号更加不规则,所以排列熵较大,参考文献[12]的论证结果,本文在对固有模态分量进行检测时选取排列熵为0.6。

表1 几种信号的排列熵
1.3 基于奇异值分解的循环策略
在噪声信号先验知识未知的情况下,对于固有模态分量中信号的有效提取是个难题。根据论文1.2节排列熵分析,本文提出了基于奇异值分解的循环策略对有用信号进行提取,具体步骤如下:
(1)对含噪信号进行CEEMD处理,得到一系列本征模态分量ci(t)和余项rn(t)。
(2)对ci(t)进行排列熵检测,若PEi>0.6,则认为第i个IMF为噪声主导,若PEi≤0.6,则认为第i个IMF为信号主导。
(3)对噪声主导IMFs进行奇异值分解,由奇异值分解基本原理可知[13]:信号经奇异值分解,得到1-d个奇异值分量,前面较大的k个奇异值由纯信号和噪声共同贡献,其对应的奇异矢量所张成的空间即为加噪信号子空间,后面相对较小d-k个奇异值完全由噪声贡献,将其剔除,可以减少含噪信号中的噪声,奇异值分解降噪关键在于k值得选取,可以做个假设:若重构前k个奇异值分量得到的信号排列熵不大于0.6,则认为奇异值分解有效重构阶次为k,由EMD的原理可知,第一IMF包含了绝大部分噪声,会出现只重构第一个奇异值分量仍不能满足其排列熵检测的情况[14],因此需要设计一个循环策略,提取第一个奇异值分量继续进行奇异值分解,直至满足排列熵检测,循环过程如图1所示。
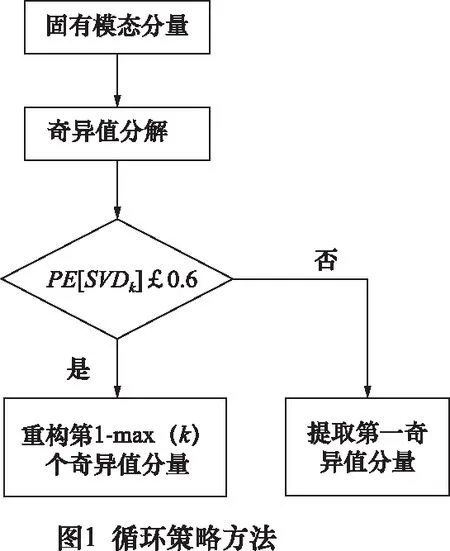
图1中PE[SVDk]表示前k个奇异值分量的排列熵,max(k)表示满足PE[SVDk]≤0.6时k的最大值,目的是为了尽可能减少降噪过度。
(4)经步骤(3)处理后,可得到一系列信号主导分量,最后经过平滑滤波,去除信号中的毛刺、尖锐部分,得到降噪后的信号,考虑到Savitzky-Golay滤波是一种滑动窗口中心点的有效拟合方法[15],本文选用SG滤波方法对信号进行平滑处理。
2 仿真和应用分析
2.1 仿真验证分析
对Lorenz方程
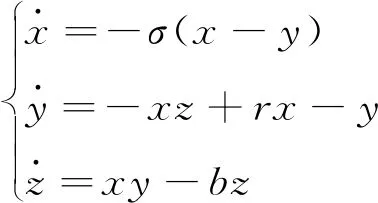
(6)
取参数σ=10,r=28,b=8/3时,是一种混沌信号[16],积分步长为0.01,采用四阶龙格-库塔算法运算,取1 000个样本点,干净信号和含噪信号如图2所示。
图3为Lorenz含噪信号的CEEMD结果,分解为8个本征模态分量(imf1~imf8)和一个余项ri(t),高频部分没有明显的信号混叠特征,说明了经过白噪声多次叠加和平均,克制了信号中的伪极值点,减少了模态混叠。图4分别为传统CEEMD方法、CEEMD-小波阈值方法和本文方法的降噪结果,传统CEEMD方法是直接将噪声主导的本征模态分量剔除,重构信号主导的本征模态分量,CEEMD-小波阈值方法是利用小波阈值处理提取噪声主导的本征模态分量中的有用细节,然后和号主导的本征模态分量叠加达到降噪目的,图5为3种方法降噪后的重构误差,即是降噪后信号和干净Lorenz信号的差值,三种方法的重构误差分别为0.147、0.051 6、0.040 2,通过比较可以看出,传统CEEMD方法的重构误差明显高于其他2种方法,其在去除高频噪声的同时,也会使其中的信号丢失,增加了信号失真,所以其重构误差中明显包含了有很多有用信号特征;CEEMD-小波阈值方法将阈值以上的信号保留,会使部分噪声遗留,尤其是对于噪声主导的信号,效果很不理想,图4b中信号明显留有粗糙细节,也印证了这一论述;本文方法是一种多次筛选提取信号的方法,即使是低信噪比的信号,经过多次循环筛选,也可以有效将隐藏其中的信号提取出来,并且相比上述两种方法,本文方法降噪后信号更加光滑,重构误差最小,证实了所提方法的优越性。
为了进一步验证所提方法的优越性,本文通过信噪比(SNR)、均方误差(MSE)分析上述两个参数的选取,2个参数的计算公式如下:
(7)
(8)
其中:x′(n)表示去噪后的序列,x(n)为原始时间序列,var(·)表示方差,x′(n)-x(n)表示信号中的剩余噪声。信噪比反应去噪能力的大小,均方误差的物理意义是表示去噪后信号和原始信号的平均偏离程度,通常认为,SNR越大,MSE越小,说明去噪效果越好。
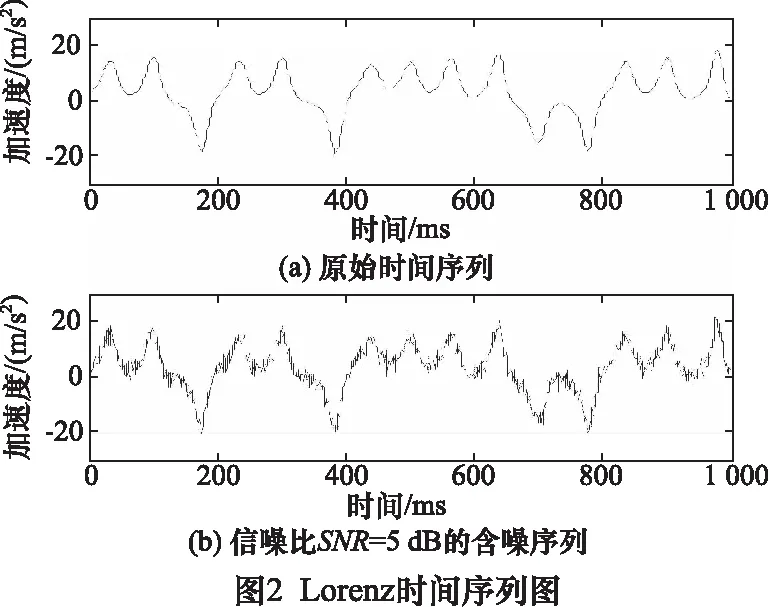
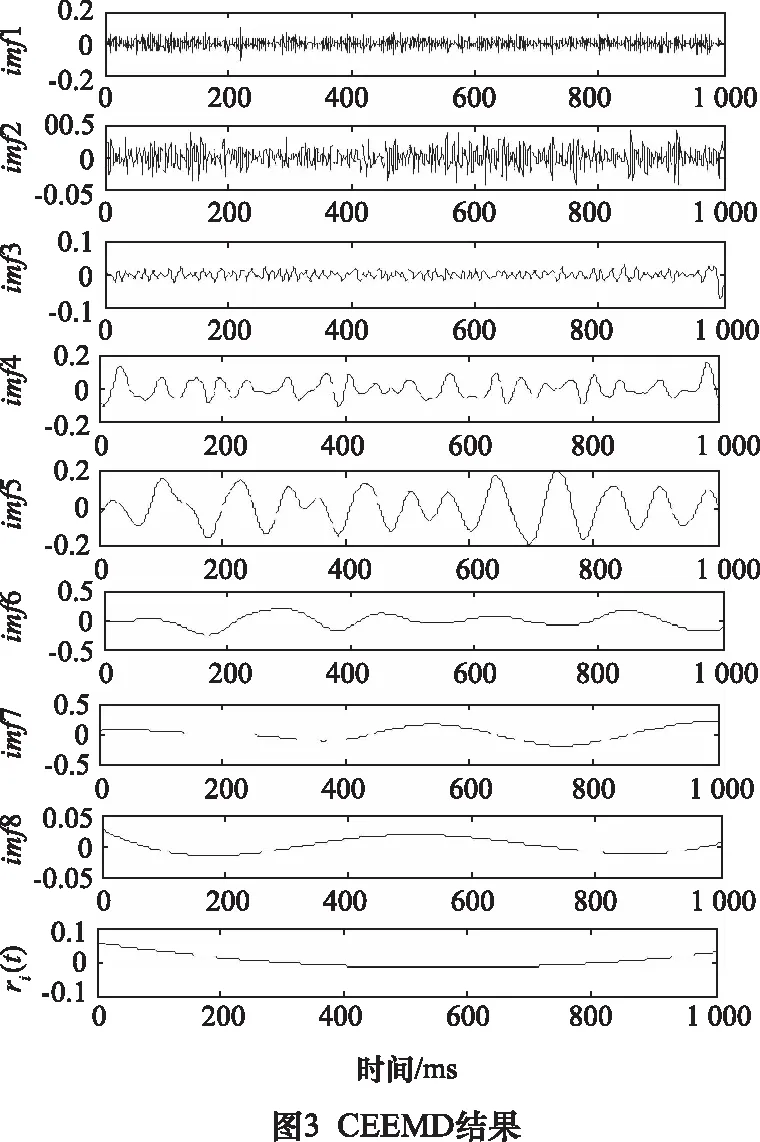
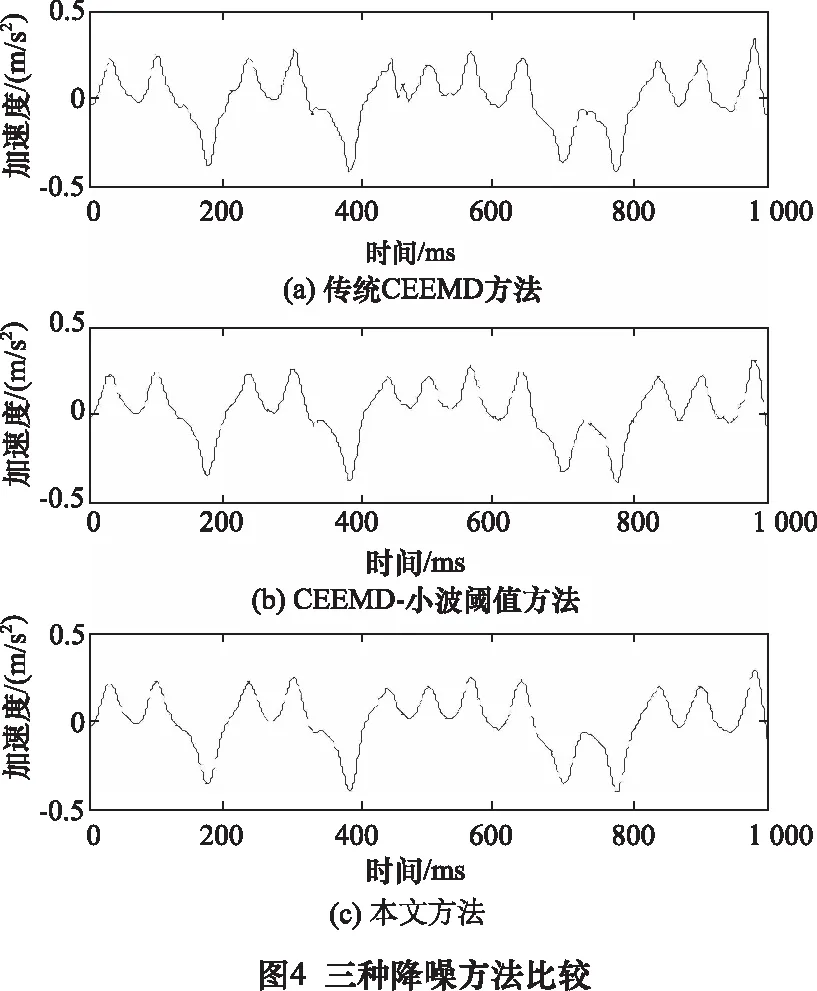
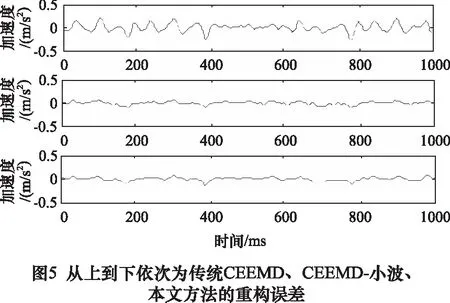
表2给出了EEMD、传统CEEMD方法、CEEMD-小波阈值方法和上述3种方法降噪的各项指标。可以看出,本文方法降噪后信号信噪比最高,均方根误差最小,体现了所提方法对于低信噪比信号提取的优越性;同时,表2是同步比较3种方法的计算时间,CEEMD是同时叠加相反的白噪声,所以叠加噪声总次数和EEMD一致,可以看出CEEMD时效性较EEMD有很大的提升,本文方法由于增加了基于奇异值分解的多次循环提取信号,所以计算耗时有所提升,但是所提循环策略是一种自适应的手段,且奇异值分解运算简单,因而总耗时增加不多,但降噪后信号信噪比却比CEEMD-小波阈值降噪方法提升了近1dB。
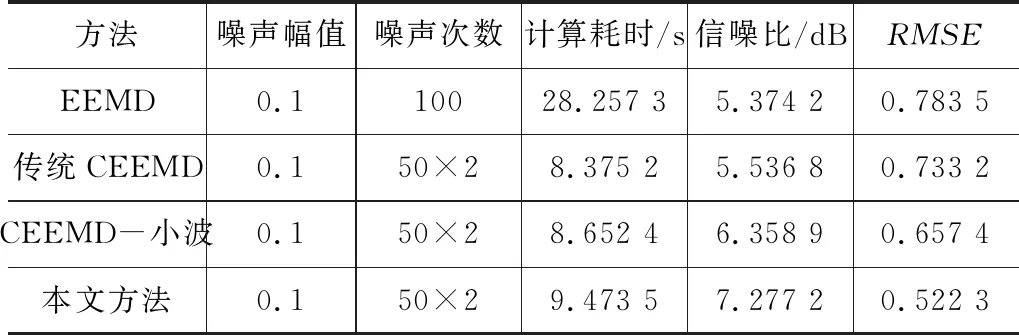
表2 4种方法各项指标比较
2.2 应用分析
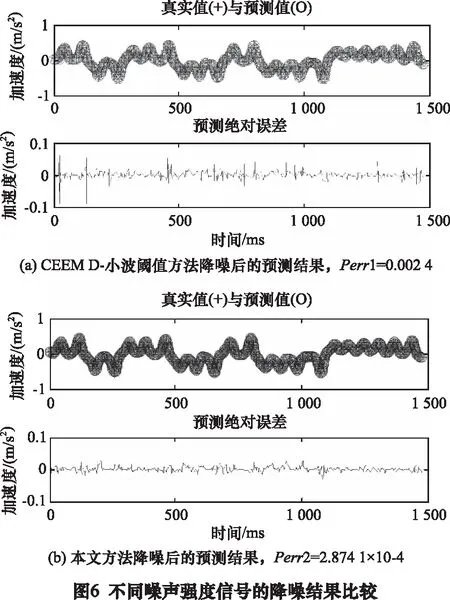
对CEEMD-小波阈值和本文方法降噪后的含噪Lorenz信号利用Volterra预测模型进行预测,预测绝对误差分别为Perr1=0.002 4、Perr2=2.874 1×10-4,可以看出同一预测模型下本文方法将预测精度提升了一个数量级,且图6a中的误差曲线有几个峰值误差接近0.1,这种大误差点很可能导致混沌预测在应用中出现错误结论,而6b中预测误差曲线没有特别明显的误差峰值。
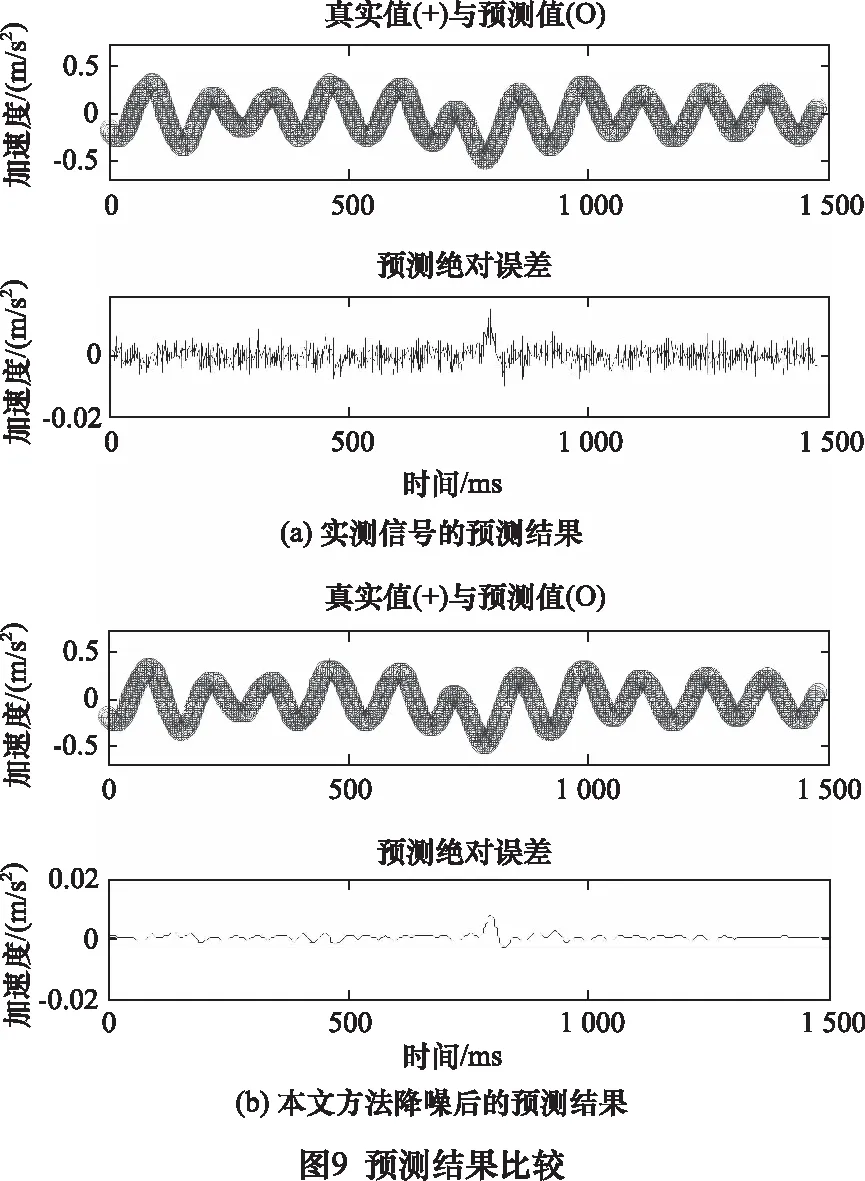
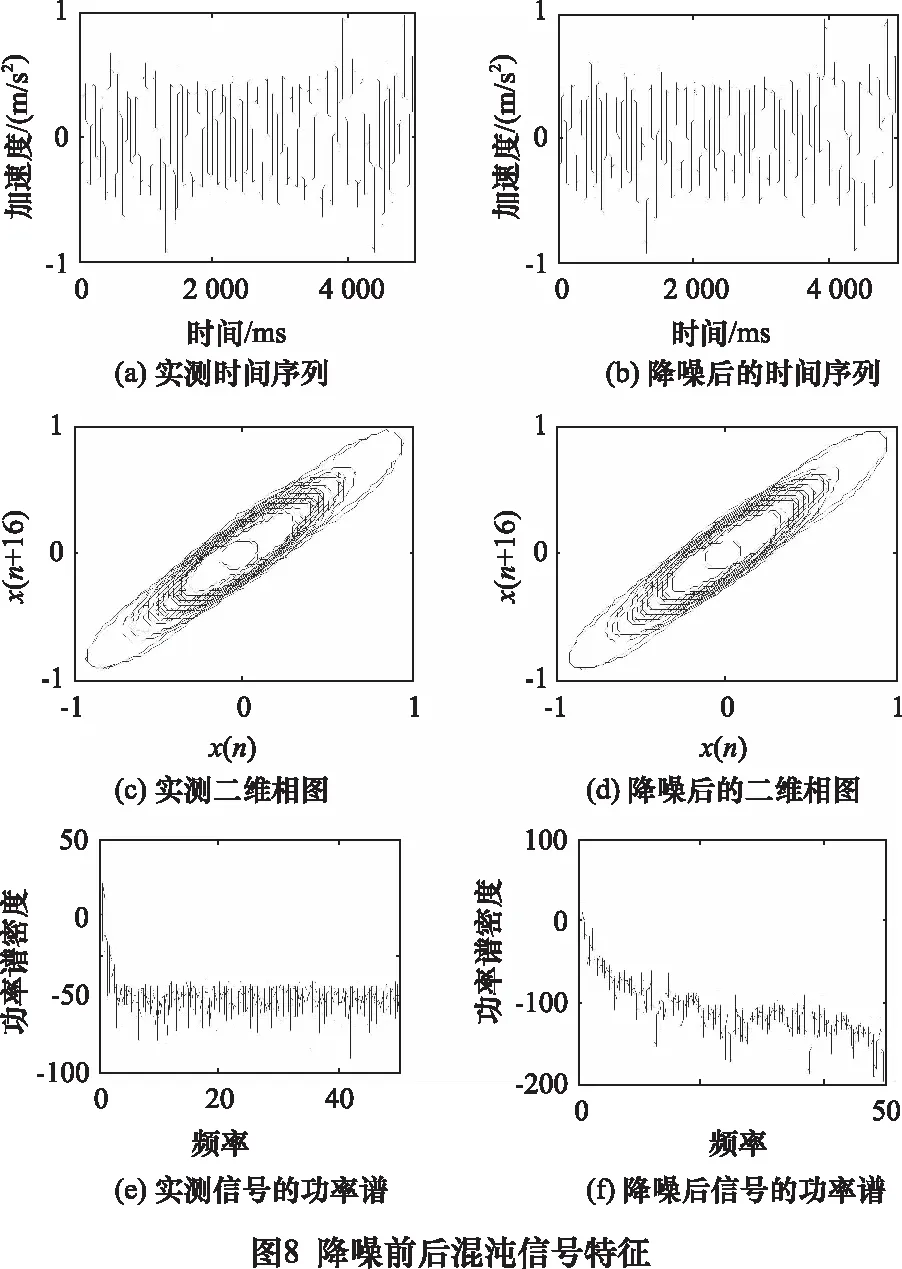
混沌振动特征分析是混沌工程实际应用的关键环节,基于实验室条件下的混沌运动特性分析也是将混沌应用于工程实际的重要前提,为此,以文献[17]产生的混沌信号为对象,验证所提方法对实测混沌信号的适用性,试验实物图如图7所示,当激励增益为1V,激励频率为9.8 Hz时,实测时间序列如图8a所示,嵌入维数为4,延迟时间为16,得到混沌吸引子相图如图8c所示,利用所提方法降噪前后实测信号的功率谱和预测结果8e、f和图9所示,可以看出,降噪后预测绝对误差大大减小,证实了本文方法对无论仿真信号还是实测混沌信号都是有效的,同时证实了本文方法可为混沌运动分析提供了有效的预处理手段。

3 结语
提出了基于CEEMD-排列熵的循环策略信号提取方法。CEEMD较于EEMD,在抑制白噪声引起重构误差的同时简化了计算方法,对分解得到的本征模态分量通过计算排列熵确定噪声分量和信号分量,在奇异值分解的基础上,建立循环策略的信号提取方法,该方法无需信号和噪声的先验知识,在抑制噪声的同时,可以较好地保留有用信号。通过仿真信号和实测混沌信号降噪处理,结果表明所提方法较EEMD时效性有很大的提升,降噪效果较CEEMD-小波阈值提升了近1 dB,且本文方法对较低信噪比信号的有更好的降噪效果,并可为混沌实测信号特征分析提供有效的预处理手段。