直线电机进给系统动态性能演化规律数值模拟与试验
杨泽青,田建忠,陈英姝,刘丽冰,魏强*,
(1. 河北工业大学 机械工程学院,天津 300130;2. 河北工业大学 高端装备结构技术研究院,天津 300401)
直线电机进给系统作为典型的复杂机电耦合系统,其动态性能反映了系统抵抗动态外载荷的能力,与抗振性密切相关,直接影响系统进给运动精度和控制精度[1]。另外,随着数控机床不断向高速度、高精度和高可靠性方向发展,对进给系统的动态性能也提出了更高的要求,直线电机进给系统长期在高速、高加速度、变速、变加速度、振动、变载、启停等复杂工况环境下服役,导致其动态性能及状态转移的随机性更强,研究复杂工况下直线电机进给系统动态性能演化规律具有重要的理论意义和应用价值[2]。
关于机床进给系统动态性能演化规律的研究主要有理论建模分析法[3-16]和复杂系统机电耦合分析法[17-19]等,如Remy等[3]采用因果顺序图在考虑电磁力谐波情况下对永磁直线同步电动机进行建模。Yang等[4-5]采用麦克斯韦方程和电磁能量法获得直线电机推力谱,分析了不同运动参数下各推力谐波的多维变化及推力谱对位移波动的影响,实验表明在不同运动参数和载荷下的推力谐波表现出多维的频谱特性,为高速高精密数控机床直线电机进给伺服系统的运动参数选择及伺服控制参数优化提供理论依据。Kim等[6-7]发现滚珠-丝杠伺服进给系统性能取决于机械和控制系统之间的相互耦合作用。Whally等[8]采用集中参数与分布参数法建立了滚珠丝杠进给系统机电耦合数学模型,考虑丝杠的柔性,对空载与切削扰动下机床的动态性能进行仿真分析,并结合实验分析了影响机床动态性能的因素。Liu等[9]基于频率特性研究了直线电机进给系统动态性能,并给出了系统瞬态、稳态运动精度的分析方法。Pashkevich 等[10]从理论建模和仿真角度分析了不同结构形式并联机床的刚度分布情况。Yu等[11]考虑不同载荷下变刚度特性建立并联机床动力学模型,得到变截面构件刚度和质量矩阵,对其动态性能进行试验研究,发现低频振动对并联机床稳定性有重要影响,为合理选择主轴转速和轴向切削深度以避免颤振提供理论依据。Song等[12]采用缩比模型预测了五自由度混合机床的动态性能,并考虑了轴承的几何变形对其动态特性的影响。刘海涛与赵万华[13]提出了基于广义加工空间概念的整机刚度场概念,利用矩阵摄动法分析了刀尖点在全参数下的模态演变规律及刚度场变化。Fedorynenko等[14]采用传递矩阵法仿真分析了超精密机床主轴动态特性,确定了水润滑液的供给压力、静压轴承的径向游隙和轴径对主轴转子系统振动和共振频率的影响规律。付振彪等[15]基于Hertz接触理论计算滚珠丝杠进给系统的各结合面参数并建立整个进给系统有限元模型,仿真分析了主轴质量、滚动导轨副预紧力及滑块间距对进给系统振型分布和固有频率的影响。Xu等[16]考虑整体轴向变形的解析分段恢复力建立车床滚珠丝杠进给系统动力学模型,并采用改进的一次二阶矩法(AFOSM)评估系统的动态响应误差,讨论了外部激励、滑动平台位置和标称接触角对动态响应的影响,根据实际转向精度分析了可靠性和灵敏度。Neugebaue等[17]在ANSYS中建立机械系统与伺服控制系统的机电耦合模型,考虑机床进给轴的级联控制模式对进给伺服系统机电耦合动态特性进行仿真,通过模态测试验证了模型的准确性。西安交通大学的卢秉恒院士[18]带领的课题组从进给系统机电耦合角度研究其动态特性,取得了重大突破,为高速高精度机床进给系统各部分的特性变异规律、动态特性优化、演化及机电耦合的本质机理研究奠定理论基础。杨晓君等[19]应用达朗贝尔公式建立直线电机进给系统工作台的动力学模型,分析直线电机进给系统动态特性的影响因素,得出机械环节刚度、伺服控制参数及进给速度会影响进给系统机械动态特性,同时也会影响控制系统输出的电磁推力,最终电磁推力、控制参数、进给速度等共同影响直线电机进给系统的运动精度。杨毅青等[20]研究了基于动力学特性与切削特性耦合的机床结构设计优化方法。姚延风、刘强等[21]提出了一种考虑刚柔-机电耦合作用的机床直线电机进给系统动态性能建模仿真方法,实现在数控机床设计阶段研究机械结构和伺服控制系统的相互作用,考虑伺服控制参数对机床动态性能的影响。
以上研究成果对理解和分析数控机床伺服进给系统性能保有阶段动态特性具有重要作用,但是在系统高速高加速运行或启停换向过程中由于机械传动部件空间位置变化而导致的动态性能演变规律及复杂性鲜有研究,为此本文尝试从数值模拟和试验角度,研究工作台不同位置处进给系统动态性能演化规律,为进给系统动态性能退化机理和性能预测维护奠定基础。
1 直线电机进给系统动力学模型
以两轴联动直线电机进给系统为研究对象,其中X轴与Y轴“十”字正交,且X轴在下、Y轴在上,Y轴与X轴的动子耦合在一起。根据达朗贝尔原理建立X轴的进给系统动力学模型[18]为
(1)
式中:m为系统的质量矩阵;cB为系统的阻尼矩阵;k为系统的刚度矩阵;F为系统所受的外力;X=(xyzθxθyθz)为工作台质心的位移,其中x、y、z分别为质心沿X、Y、Z坐标轴的位移,θx、θy、θz分别为质心绕X、Y、Z坐标轴的转角位移。
直线电机进给系统在运动过程中,机械系统部分的位置是不断变化的,Y轴在不同位置处时,整个机械系统的质量分布是不同的。随着位置的变化,由于轴间耦合的存在,相应轴的转动惯量也发生了变化。由于结合面刚度非线性以及摩擦阻尼的影响,机械系统的质量分布会随着位置的不同发生偏移。此外进给系统在启动、停止和换向等运动过程中,惯性力也是不断变化,这些都会对机械系统的动态性能产生非常重要的影响。也就是说由于空间位置不同,系统的动力学方程中的系数矩阵均是不断变化的,这会直接影响进给系统的传动精度以及稳定性[18]。
当工作台处于不同位置时,系统的质量矩阵发生变化,工作台处于最左端、中间和最右端位置处系统的质量矩阵分别为m1、m2、m3,其表达式分别为:

(3)
式中:mx、my、mz分别为工作台质量和电机动子质量在X、Y、Z方向的分量;m为工作台和电机动子质量之和;Jx、Jy、Jz为工作台惯量;s(x)为工作台中心距离系统质心之间的X向位移。
刚度矩阵k和阻尼矩阵cB的表达式分别为:
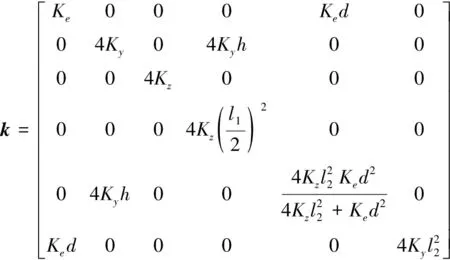
(5)

(6)
式中:Ke为进给伺服刚度;Ky、Kz分别为滑块在y、z方向的刚度;Cx、Cy、Cz、Cθx、Cθy、Cθz分别为工作台在x、y、z方向的平移和转动阻尼;l1为导轨间距;l2为相邻两滑块间距;d为电机动子下表面到工作台整体重心的距离;h为滑块到工作台整体中心的距离[19]。
2 进给系统动态性能数值模拟分析
本文研究的两轴联动直线电机进给系统X、Y轴运动行程均为800 mm,最大移动速度为200 mm/s,最大加速度2 g;在建立各轴动力学模型基础上,利用ANSYS Workbench软件对进给系统进行模态分析。设置直线电机进给系统的内部长导轨为GCr15(密度为7 800 kg/m3,弹性模量为20.8 GPa,泊松比0.3),其余零部件为铝合金(密度为2 770 kg/m3,弹性模量为71 GPa,泊松比0.33)。进给系统存在许多的连接孔洞和工艺槽等结构,不利于网格划分和提高计算精度,因此对进给系统作了必要的简化,最终得到包含404 236个节点220 912个单元的直线电机进给系统有限元模型,模型如图1所示。

图1 直线电机进给系统有限元模型
直线电机进给系统的导轨滑块与长导轨的结合面采用弹簧-阻尼柔性单元进行等效,结合面等效动力学模型如图2所示。
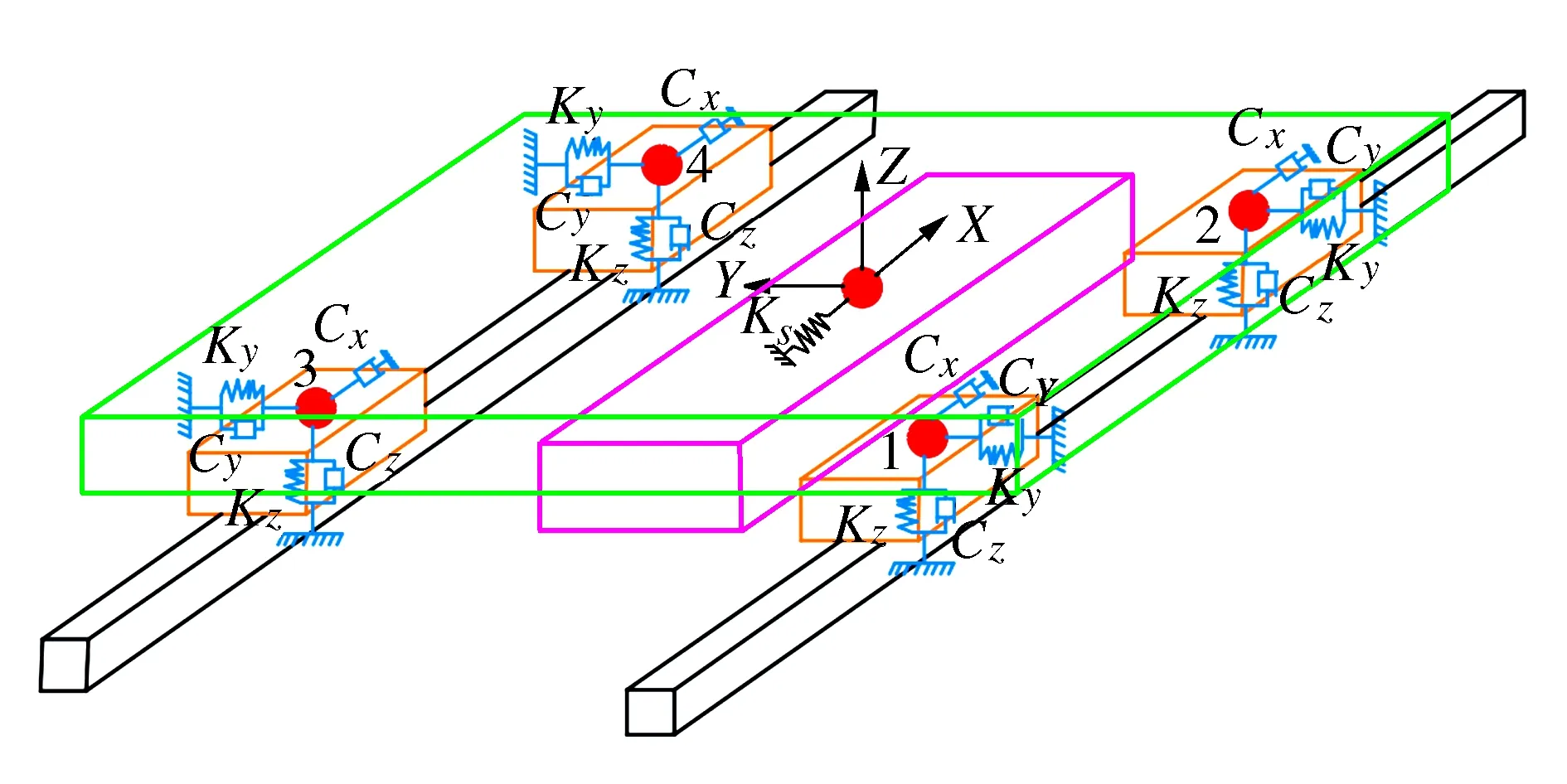
图2 直线电机进给系统结合面动力学模型
结合面的参数计算采用吉村允孝法,结合面的等效动力学参数可以通过单位面积值的动态数据对结合面的面积求积分获得。各结合面参数值如表1所示,其余的结合面均采用默认的刚性固定连接方式。

表1 导轨结合面参数
数值模拟计算直线电机进给系统在3种不同位置的前4阶固有频率及振型,如表2所示。
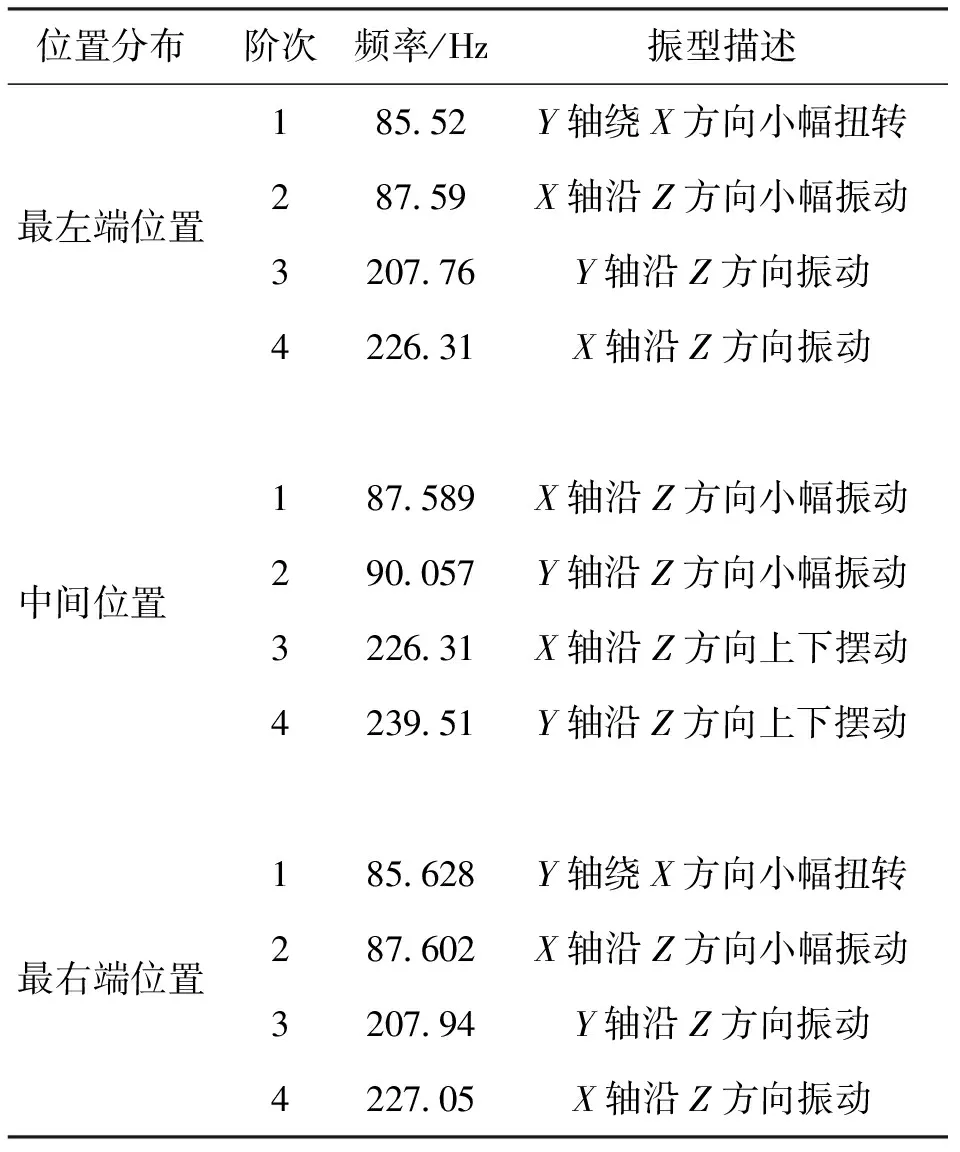
表2 进给系统不同位置前四阶固有频率及振型
进给系统在不同位置的同阶(第3阶)振型对比如图3所示。
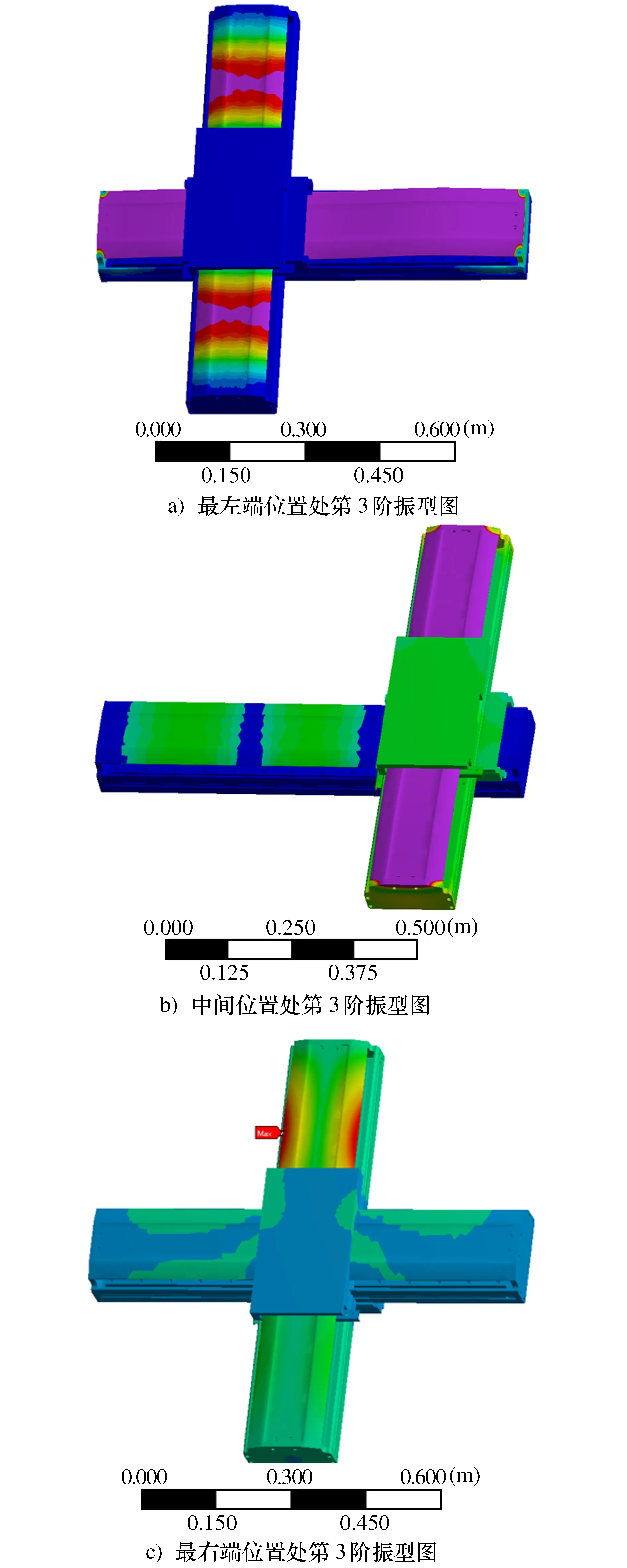
图3 进给系统不同位置处同阶模态云图对比
由表2和图3可知,直线电机进给系统工作台处于最左、右侧位置分布时系统前4阶固有频率和振型基本一致,但工作台处于中间位置时前四阶固有频率稍高于最左、最右侧相应的前4阶固有频率,振型也发生了变化,振幅相对于左右两侧有所降低,说明工作台处于中间位置时系统的动态性能得到改善。数值模拟分析发现,随着进给系统工作台空间位置发生变化,由于轴间结构耦合作用,会引起机械系统的质量分布变化,当工作台沿着X轴运动到不同的位置状态时,相应轴的转动惯量发生变化,导致其动态性能发生演变。
另外,在电磁推力和伺服刚度协同作用过程中,工作台处于运行状态中,滑块与导轨组成的运动部分是在电磁力的作用下实现进给运动,运动过程中随着位置的改变,质量分布发生变化,但是电磁推力在瞬时状态下很难发生改变,因此在进给方向上会出现电磁力不均衡现象,因此会产生一定频率的振动,振动产生后导致接触面的气隙变得不均匀,使得工作台两端的吸引力存在差别。
3 进给系统模态测试试验验证
为了验证直线电机进给系统有限元模型模态分析和动态性能演化规律的准确性,利用LMS测试分析系统对位于精密运动控制平台上的直线电机进给系统进行锤击法模态测试试验,选用工作台位置单点力锤激振、多点加速度传感器拾振的方式。响应信号通过粘连在进给系统不同位置处的PCB加速度传感器拾取振动信号,由LMS采集系统进行信号处理得到各测点处的频响曲线,图4为现场试验图。

图4 进给系统模态测试试验
试验测得的工作台处于不同位置处直线电机进给系统的频响曲线如图5所示,并与模态数值模拟分析结果进行对比分析,如表3所示。
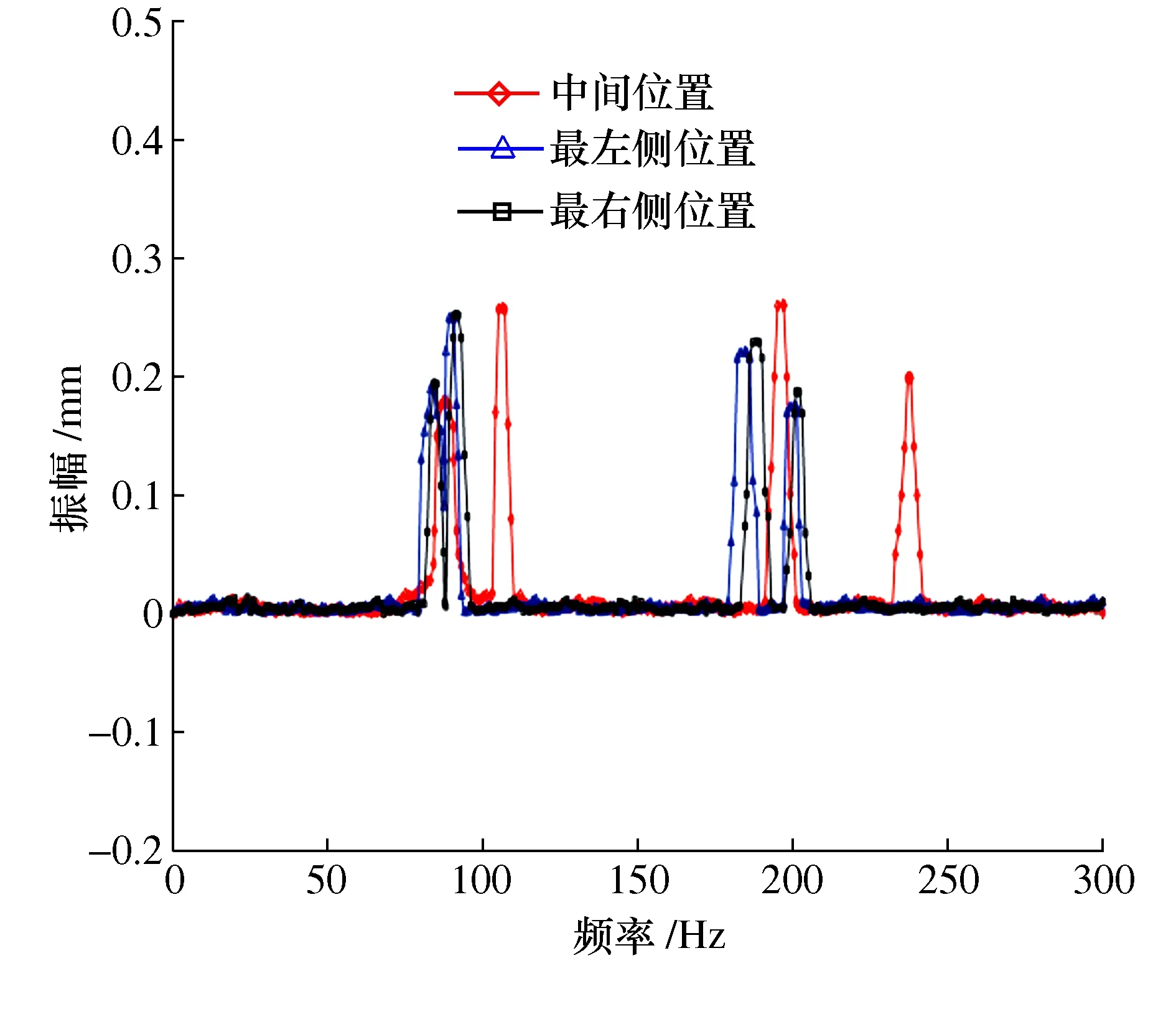
图5 进给系统模态测试固有频率

表3 试验结果与仿真结果数据对比
由图5和表3可知,试验结果和仿真结果变化趋势相近,工作台处于不同位置处波峰值频率对应较好,验证了该有限元模型的准确性,为直线电机进给系统动态性能演化规律研究奠定了基础,试验所得到的模态振型在有限元分析的结果中都可以找到相匹配的模态振型,且相同的模态振型的固有频率差距在可允许误差范围以内,对比的结果显示仿真的数据误差较小,说明了仿真分析满足了进给系统模态分析的要求。
4 不同机械质量分布对动态性能影响
由有限元模态数值模拟分析和模态测试试验结果可知,直线电机进给系统动态性能主要是由以下几类因素影响:
1) 不同机械质量分布必然会引起质量矩阵发生变化,这直接影响进给系统的动态性能,在复杂工况下,进给系统的位置是不断变化的,那么根据多种位置的不同,以此分析几个特定位置处的固有频率以及振型变化。通过具体分析发现,直线电机进给系统同阶固有频率会伴随着进给系统的质量分布变化而变化。因此运行使用过程中,需要根据工况条件合理调整质量分布方案,均化系统各阶模态柔度所占比重,这样才能够提高系统整体的运动精度和稳定性。
2) 不同机械质量分布会引起导轨滑块支撑刚度矩阵发生变化,在高速高加速运行下,由于机械系统运动部件的惯性力使结合部的负载发生变化,不同加速度下动结合部非线性的作用造成刚度不同,进而导致结合部刚度发生变化或突变,那么工作台在运行过程中处于不同位置会存在俯仰、横向等不同振动形式;其次伺服动刚度也会影响系统整体的动态性能,伺服动刚度一般是由控制参数选择、控制结构、外部干扰协同影响的,在进给系统启动、停止和换向等运动过程中伺服推力发生变化以后,那么伺服动刚度也会发生改变,这样直接影响进给系统的动态响应。
因此,直线电机进给系统在运动方向上对应的振动频率会被伺服动刚度所影响,如果增加振动频率,那么伺服刚度也会增加,在此期间,俯仰振动频率处于平缓阶段。同时,直线电机在出现推力波动的时候,将会发生周期性变化,这是因为受到了齿槽和端部效应作用,在速度变化期间,推力频率特性也在变化,从而这些特性会影响工作台的具体运行特性。
5 结论
为确定复杂工况下随工作台移动直线电机进给系统动态响应演变规律,采用数值模拟及模态测试试验研究工作台处于最左端、中间、最右端位置处的直线电机进给系统动态响应,得到以下结论:
1) 直线电机进给系统工作台处于最左、右侧位置分布时系统前4阶固有频率和振型基本一致,但工作台处于中间位置时前4阶固有频率稍高于最左、最右侧相应的前4阶固有频率,振型也发生了变化,振幅相对于左右两侧有所降低,说明工作台处于中间位置时系统的动态性能得到改善,究其原因在于随着工作台位置的变化系统质量分布出现偏移导致其动态性能发生演变。
2) 在高速高加速复杂工况下不同机械质量分布会引起导轨滑块支撑刚度矩阵发生变化,另外系统伺服动刚度也会影响系统整体的动态性能,因此下一步需要考虑复杂工况下机械系统与控制系统机电耦合作用对进给系统整体动态性能的影响及演化规律。

