铝板在双面喷流加热和辊底摆动过程中的温度均匀性

赵延涛， 姜泽毅,2， 张欣茹,3， 王帝杰

(1. 北京科技大学 能源与环境工程学院， 北京 100083;2. 冶金工业节能减排北京市重点实验室， 北京 100083;3. 北京高校节能与环保工程研究中心， 北京 100083)

铝合金板材热处理过程中的加热工艺会直接影响材料温度分布和升温规律，进而改变其内部组织结构和基本性能[1-3]。在铝板加热设备及其工艺研究中，一般通过改善供热装置布置、炉气循环和导流等方式来提高加热过程板温均匀性。近来，一些研究者将多孔喷流加热技术引入铝合金加热炉中，强化铝板表面换热，并期望进一步提高加热均匀性。张超纲等[4]发现喷流加热工艺与传统热风循环加热工艺相比，铝合金棒料加热温度均匀性好，表面温差可控制在±3 ℃；同时，加热速度快，加热时间可缩短约46.6%。李家栋等[5]研究发现，强风气垫冲击喷流加热铝板的对流换热特性，基于集总热容法，获得了喷流速度在42～68 m/s区间内，表面对流换热系数与铝板温度的关系，建立了平均对流换热准数方程。从根本上来说，喷流过程的换热特性会对加热过程及工件的温度均匀性产生影响。

众多学者对喷流过程的换热特性进行了模拟和试验研究，通过参数分析获得了各种强化换热的措施。例如陈平安等[6]研究了多喷口空气淹没射流的换热特性，分析了喷口高度、速度、间距等因素对换热的影响。Zhou等[7]、Geers等[8]研究了喷口排布方式、喷口和平板间距离对换热的影响，结果表明喷口高度不同时所对应的最优排布方式也不同。Terekhov等[9]、Burak等[10]发现环形射流会产生更多的涡流，进而增强热量和质量传递。Alekseenko等[11]、Nuntadusit等[12]研究表明旋流射流能显著强化换热，且速度场及温度场分布更加均匀。

迄今为止，针对板材加热过程均匀性问题的研究主要集中在敞焰加热炉，并探讨了燃烧方式、辐射遮蔽、旋流等因素的影响。Rene等[13]采用迭代求解的方法，交替模拟了燃烧和钢坯的瞬态传热，结果表明辐射换热对钢坯温度均匀性的影响远大于对流换热。Mayr等[14]针对推钢式加热炉，将钢坯视为连续流体，分析了旋流燃烧器旋转方向对钢坯温度分布不均的影响。齐凤升等[15]采用动网格方法模拟了钢坯运动，解决了钢坯运动问题和加热炉与钢坯的耦合传热问题，分析了垫块结构对钢坯温度均匀性的影响。然而，有关不同参数对铝板喷流加热中炉内换热及板温均匀性影响的研究，目前还鲜有报道。

本文基于辊底式铝板淬火炉加热工艺，针对板材双面多喷口气体喷流换热与内部导热的耦合问题，建立了板材喷流加热过程的数理模型；模拟了炉内换热过程，并将换热系数作为边界条件代入铝板导热模型，获得了铝板温度变化规律；并以此为基础，分别探讨了不同喷口排布、热风流量、铝板厚度和辊底摆动周期对板温均匀性的影响。本研究为进一步明晰铝板喷流加热中不同参数对板温均匀性的影响提供了参考。

1 数学模型

1.1 加热工艺及模型简化

在辊底式铝板淬火炉中，板材放置在辊道上，被热风双面喷流加热，热风加热铝板后，通过喷口间的缝隙由循环风机抽出，经加热后再均匀分布到各喷口中。加热过程中，辊道正向、反向往复旋转，使铝板纵向来回摆动，以提高铝板温度均匀性。图1为铝板辊底式喷流加热工艺示意图，其中喷口直径为φ100 mm，沿炉长和炉宽方向间距均为450 mm；辊道直径为φ290 mm；铝板摆动一个来回所需要的时间即为摆动周期。

图1 铝板辊底式双面多喷口喷流加热工艺的示意图

由于加热过程中板材来回摆动，很难将喷流换热过程与铝板内部导热直接耦合求解，因此对其分开模拟。对于喷流换热过程，由于喷口排布具有规律性，为简化计算，数值模拟时选取单元空间作为计算域，如图1 中的绿色(上炉膛450 mm×450 mm)和黄色(下炉膛450 mm×450 mm)区域，进而获得铝板表面换热系数分布。

对于铝板导热过程，由于炉宽方向的周期性特点，选取450 mm宽度作为计算域，建立沿板厚和宽度方向非稳态二维导热模型，铝板上下表面的换热系数根据板坯摆动位置和喷流换热数值模拟结果来确定。

1.2 喷流换热和铝板导热模型

对于喷流换热过程而言，辊底炉内气体流动及换热的过程满足质量、动量及能量守恒方程，即

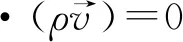
(1)

(2)

(3)

本文采用Realizablek-ε湍流模型模拟喷流平板的流动换热，其形式为：

(4)

(5)

喷流换热过程的主要边界条件：铝板表面为定壁温，辊道表面为绝热，炉宽方向端面为周期性边界条件，炉长方向端面为对称面。

对铝板导热过程而言，建立了沿铝板宽度(x)和厚度(y)方向上的二维铝板非稳态导热模型。导热微分方程为：

(6)

式中：λ为导热系数，W·m-1·K-1；c为比热，J·kg-1·K-1。

铝板导热过程的边界条件：

(7)

(8)

(9)

(10)

式中：d为铝板厚度，m；l为铝板计算域宽度，m；Ts为铝板表面温度，℃；Tf为炉气温度，℃；hup、hdown分别为上、下表面换热系数，W·m-2·K-1。

1.3 数值模拟和工况参数

喷流换热和导热模型均采用Fluent软件进行求解。其中，喷流换热模型的上、下炉膛单元空间分别采用六面体网格和多面体网格。网格无关性检查后，最终上、下炉膛网格数量分别为160万和70万。基于上述模型，本文首先研究了4种喷口排布方式下的换热特性，获得了铝板表面换热系数分布，并将其代入导热模型中，获得了最优喷口排布方式；再针对最优喷口排布方式，又研究了热风流量(0.175和0.292 m3/s)、辊底摆动周期(27.2和272 s)对不同厚度(4和80 mm)板材温度分布的影响。

2 试验结果与讨论

2.1 模型验证

基于文献[16]的数据，建立了单喷口喷流换热模型，喷口距平板高度与喷口直径之比H/D=2.5，D=100 mm。本文模拟结果与试验结果对比如图2所示，其中r/D表示无量纲径向距离(平板表面某位置距喷流驻点的径向距离与喷口直径之比)。可以看出，一定雷诺数Re下，模拟计算得到的局部努塞尔数(Nu)与文献中的试验值吻合良好；不同雷诺数下，模拟计算得到的驻点Nu也能与试验值吻合较好。总体看来，模拟值与文献试验值的最大误差均在15%以内；因此，所建模型适用于喷流平板流动换热的预测。

图2 模拟结果与文献[16]中试验值的对比

2.2 不同喷口排布方式下的换热特性

4种不同喷口排布方式如图3(a1～a4)所示，虚线框内为实际所取的计算域，其中：方式1(见图3(a1))喷口为正方形点阵排列，沿炉长和炉宽方向上，喷口间距均为450 mm，喷口为垂直喷流；方式2(见图3(a2))喷口排布与方式1相同，但喷口为倾斜喷流，喷口轴线与竖直方向夹角为17°；方式3(见图3(a3))为垂直喷流，喷口不完全错排，在炉宽方向上每个喷口都位于相邻一排喷口之间的1/4距离处(称为1/4间距错排)；方式4(见图3(a3))也为垂直喷流，喷口完全错排，即在炉宽方向上每个喷口都位于相邻一排喷口间的1/2距离处(称为1/2间距错排)。

图3 喷口排布方式及其对应的表面换热系数分布

图3(b, c)给出了4种喷口排布方式下，单个喷口流量0.175 m3/s、炉气温度560 ℃时，铝板上下表面换热系数分布，虚线框内为简化模型实际计算结果，其余部分为周期或对称所得。可以看出，由于喷流驻点的存在，正对喷口处的板材表面换热系数小于其它区域；喷流气体交汇处流速较小，换热系数也较小。另外，倾斜喷流时，由于倾斜方向流速大，因此，该方向上的换热系数大于相反方向，且还大于相同流量下垂直喷流换热系数。下炉膛中，由于辊道阻挡了炉气流动，因此贴近辊道处换热系数极小；导致相同工况下，下炉膛板材表面换热系数要小于上炉膛。

为更好地比较不同排布方式下，板材表面换热情况，给出了相应的表面换热系数，如表1所示。可以看出，对垂直喷流而言(方式1、3、4)，上、下炉膛喷流换热系数平均值相差不大，即总换热强度相差不大；然而，由于不同方式下表面换热系数的最大值和最小值相差较大，导致加热过程的均匀性相差较大。对倾斜喷流而言(方式2)，其换热强度弱于垂直喷流，且加热过程的均匀性亦较差。这是因为，根据对流换热场协同理论[17]，喷口垂直固体壁面入射时，流场与温度场的协同程度最好，喷流换热效果最佳。

表1 不同喷口排布方式下铝合金板材表面换热系数(Wm-2K-1)

Table 1 Heat transfer coefficient of the aluminum alloy plate surface under different nozzle arrangements(Wm-2K-1)

表1 不同喷口排布方式下铝合金板材表面换热系数(Wm-2K-1)

喷口排布方式上表面下表面最大值最小值平均值最大值最小值平均值151.215.040.457.6035.7268.614.838.670.1030.5350.519.640.756.9035.7446.521.040.655.8035.3

考虑到板材在炉长方向来回摆动，板材表面任一位置处表面换热系数会随时间周期性变化，因此，将对流换热系数在铝板沿炉长方向上取平均值(把宽度方向上同一位置处所经历的所有换热系数取平均值)，进一步分析了该平均换热系数沿炉宽方向的变化。图4给出了两喷口间的平均换热系数分布(炉宽方向位置0处对应于图3中点画线所在位置)。可以看出上炉膛中，4种喷口排布方式下，平均换热系数最大值与最小值之差分别为12.4、15.6、4.1和6.9 W/(m2·K)；下炉膛中，4种喷口排布方式下，平均换热系数最大值与最小值之差分别为21.1、8.4、11.6和12.5 W/(m2·K)。平均换热系数分布越均匀，意味着加热中板材沿炉宽方向上的温度分布也就越均匀。因此，我们认为上、下炉膛喷口均以方式3排布时，平均换热系数分布更均匀，即板材表面温度分布也将更均匀。

图4 不同喷口排布方式下平均换热系数沿炉宽方向的分布

2.3 不同喷口排布方式下的板温均匀性

本文以厚度为4 mm的铝板为研究对象(加热时间2100 s，热及流量0.175 m3/s，辊底摆动周期27.2 s)，模拟分析了上述4种喷口排布方式下，铝板表面温度变化规律如图5所示，其中Ts为表面平均温度，ΔTsmax为表面最大温差。

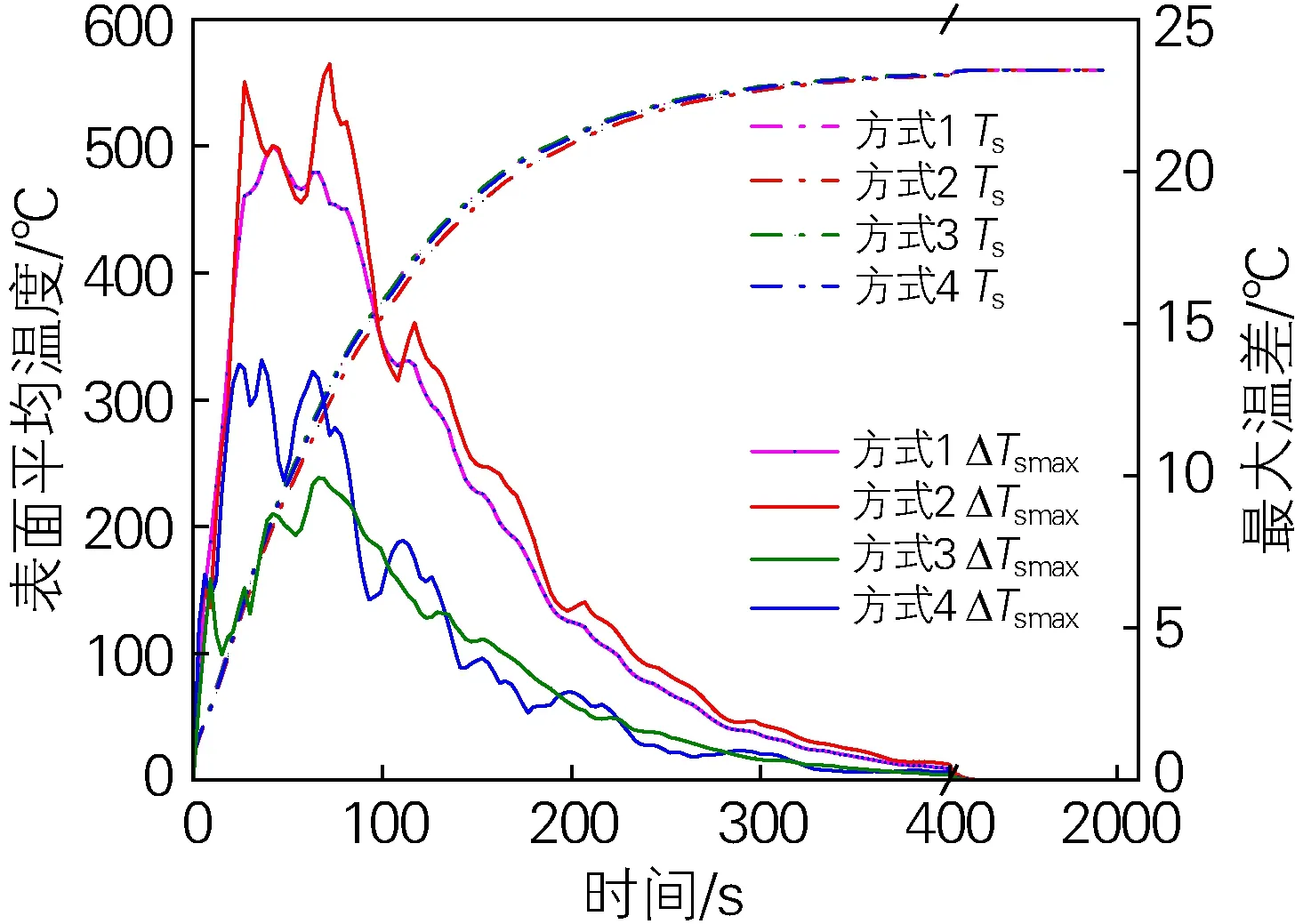
图5 不同喷口排布方式下铝板升温过程

可以看出，对于铝板表面平均温度而言，方式1、3、4下，铝板平均表面温度几乎一致，方式2稍小一些。另外，发现4种喷口排布下，加热过程表面最大温差分别为20.8、23.5、9.9和13.8 ℃；即表明方式3下铝板的换热最为均匀。其他几种排布方式，例如方式2中，表面换热系数差异显著，因此铝板温差较大；方式1中，由于沿炉宽方向上两喷口交汇处换热系数小，且考虑到不同排交汇处基本位于同一位置，因此，铝板在摆动过程中换热系数小的地方一直都比较小，换热系数大的地方一直都比较大，故温差也相对较大；方式4中，由于喷流驻点与喷口交汇处在炉宽方向上位于同一位置，即铝板摆动过程中此处换热系数也一直相对较小，使得铝板温度亦不如方式3均匀。

2.4 热风流量和摆动周期对板材升温的影响

针对最优喷口排布方式，进一步研究了热风流量对板材升温过程的影响。本文以厚度为4 mm和80 mm的铝板为研究对象(喷口排布为方式3，加热时间分别为2100 s和9900 s，辊底摆动周期分别为27.2 s和272 s)，模拟了热风流量为0.175 m3/s(热风流量1)和0.292 m3/s(热风流量2)下的铝板加热过程，如图6所示，其中，ΔTdmax为断面最大温差。

图6 不同热风流量下铝板温度变化

可以看出，加热前期，热风流量越大，铝板表面升温越快，温差也越大；加热后期，由于热风流量较大时铝板温度更高，表面热流密度较小，整体温差会减小。另外，两种规格的铝板在给定工况下均能达到加热结束时平均温度在目标温度3 ℃以内，且最大表面温差小于3 ℃的要求。0.175 m3/s热风流量下，厚度为4 mm和80 mm铝板达到该要求的时间分别为456 s和9080 s；0.292 m3/s热风流量下，达到该要求的时间分别为363 s和7320 s。

另外，本文还研究了辊底摆动周期对板材升温过程的影响。以厚度为4 mm和80 mm的铝板为研究对象，模拟了辊底摆动周期为27.2 s(周期1)和272 s(周期2)下的铝板加热过程，如图7所示。可以看出，两种辊底摆动周期下，板材表面平均温度相差不大；辊底摆动周期较长时，板材长期处于同一位置，受热不均，表面温差较大；在加热前期，辊底摆动周期越短，表面温差也越小，即铝板纵向摆动改善了板温均匀性；加热后期，辊底摆动周期对温差的影响较小。

图7 不同辊底摆动周期下铝板的温度变化

对于薄板而言，升温较快，表面温差比厚板更大，断面温差远小于表面温差；对于厚板而言，由于厚度大，升温较慢，表面温差相比于薄板要小，但需要更长的时间，才能使表面温度趋于均匀，断面温差与表面温差相当。因此，实际生产中，在加热前期可设定较短的辊底摆动周期；在加热后期可给定较长的辊底摆动周期；且薄板需要更加注意，宜采用较小的热风流量和较短的辊底摆动周期。

3 结论

本文采用数值模拟的方法研究了铝板在双面喷流和辊底摆动下的加热过程，研究了喷口排布、热风流量、铝板厚度和辊底摆动周期对板材表面换热及板温均匀性的影响。主要结论如下：

1) 喷口倾斜喷流的换热强度弱且分布不均匀，4 mm 铝板加热过程表面最大温差可达23.5 ℃。

2) 对于垂直喷流，喷口以1/4间距错排布置时，加热均匀性最好，4 mm铝板表面最大温差可降低至9.9 ℃。

3) 喷流造成的铝板表面温度不均匀主要集中在加热前期，易造成板材的变形，且对于薄板更加显著。可在加热前期采用较短的辊底摆动周期和较小的热风流量，以改善铝板表面温度均匀性。