简支铰接空心板桥梁格法模拟的探讨

梁 楠

(中咨华科交通建设技术有限公司，北京 100195)

1 引 言

简支铰接空心板桥具有预制化程度高、施工简单可靠、梁底连续平齐造型美观的优点，在我国各等级公路小跨径桥梁中有着大量的应用，在今后的桥梁工程建设中也必将继续扮演重要角色。常用的简支铰接空心板桥模拟方法是将整体受力的多梁通过横向分布系数简化为其中某一单梁的平面杆系模拟方法。这种模拟方法将空间问题转化为平面问题虽然简便但只是一种近似的处理方法[1]。如何准确模拟荷载在结构的空间分布特性从而确定结构的支撑体系、偏载对结构受力的影响等问题急待解决。梁格法是分析桥梁上部结构比较实用有效的空间分析方法，它具有基本概念清晰、易于理解和使用的特点。通过福建省道309线某简支铰接空心板桥探讨梁格法的模拟过程。

2 结构概况

桥梁上部采用2孔16 m简支铰接空心板，下部采用U台、柱式墩，扩大基础。路基宽度30.6 m，桥面宽度2 m×15.28 m，双幅桥之间设4 cm伸缩缝。设计荷载：公路Ⅱ级。预应力混凝土空心板采用C40混凝土；铰缝采用C40混凝土。不考虑桥面铺装层受力。

3 梁格法模拟

3.1 梁格法基本原理

梁格法是借助计算机分析桥梁上部结构的一种有效实用方法。它适用于板式、梁板式、箱梁上部结构及各种组合体系桥梁。梁格法的主要思路是将上部结构用一个等效梁格模拟，将分散在板式或箱梁每一区段内的弯曲刚度和抗扭刚度集中于最临近的等效梁格内，实际结构的纵向刚度集中于纵向梁格构件内，而横向刚度则集中于横向梁格构件内。从理论上讲，梁格必须满足以下等效原则：当原型实际结构和对应的等效梁格承受相同荷载时，两者的挠曲应是相等的，而且在任一梁格内的弯矩、剪力和扭矩应等于该梁格所代表的实际结构部分的内力。由于实际结构中任一方向的弯矩和该方向和正交方向上的曲率有关，而梁格法中纵横梁内的弯矩只与纵横梁曲率有关，所以梁格法也是一种近似模拟。对于钢筋混凝土或预应力混凝土桥梁，一般纵横向都配有钢筋且混凝土泊松比较小，一般在0.15～0.16，所以用梁格法对结构设计是足够精确的[2]。

3.2 梁格网格划分

利用刚度等效原则对空心板桥进行梁格划分。简支铰接空心板桥每一跨由15个空心板组成，可将这15个空心板纵向中心线位置设置成纵向梁格，纵向梁格的截面特性取对应空心板横截面特性，如图1所示。横向梁格采用空心板上下顶底板替代，横向梁格断面为矩形断面，厚度等于上下顶底板板厚相加，横向宽度一般取有效跨径的1/4～1/8，本次取1 m宽，如图2所示。

纵横向梁格抗弯刚度

Ely=E·(截面面积对y轴的惯性矩)

(1)

纵横向梁格抗扭刚度

Glx=G·(截面面积对x轴的惯性矩)

(2)

纵横向梁格抗剪刚度

GA=G·(截面面积)

(3)

式中：E为混凝土弹性模量，MPa；G为混凝土剪切模量，MPa。

图1 纵向梁格截面(单位：cm)

图2 横向梁格截面(单位：cm)

3.3 模型设置

利用有限元软件midas Civil对简支铰接空心板桥进行梁格法模拟，模型中纵横梁均采用梁单元模拟，如图3所示。每片空心板梁底部均采用弹性连接进行板式橡胶支座刚度的等效模拟，体现三个平动方向的约束刚度；纵梁间的虚拟横梁材料容重设置为0。由于空心板间没有横梁，仅靠接合缝现浇混凝土和预埋钢筋横向联系，其连接刚性很薄弱，通常视为铰接。在有限元模拟中通过释放虚拟横梁间的梁端约束，模拟形成铰接，只传递剪力不传递弯矩[3]。对纵梁从左至右进行编号依次为1#～15#梁，分别在1#、4#和8#梁跨中施加单位荷载，查看荷载横向分配情况。

图3 福建省道309线某简支铰接空心板桥梁格模型

3.4 结果对比

铰接板法是适用于简支铰接空心板桥的一种将空间问题转化为平面问题求解的方法。一般计算步骤是：(1)求一块板的截面抗弯惯性矩；(2)求一块板的截面抗扭惯性矩；(3)求板的抗弯刚度与抗扭刚度比例参数γ；(4)根据γ从表中查出幷汇成各块板的跨中荷载横向分布影响线η；(5)在影响线上将车辆荷载沿桥宽排列于最不利位置上，从而求出跨中各个荷载横向分布系数mc；(6)按杠杆法求梁端荷载横向分布系数mo；(7)桥梁全长弯矩横向分布影响线与跨中荷载横向分布影响线mc相等，桥梁中央至距桥端1/5跨度范围内剪力横向分布影响线与跨中荷载横向分布影响线mc相等，由此再作直线与桥端mo相连，作为靠桥端剪力横向分布影响线；(8)车辆荷载与横向分布系数乘积即为车辆荷载传递给某梁荷载，就可以运用平面问题理论进行求解[4]。

从梁格模型中分别提取单位荷载作用在1#、4#和8#梁跨中时弯矩和剪力影响线竖标与铰接板法影响线竖标进行对比，结果如表1、表2和表3所示。

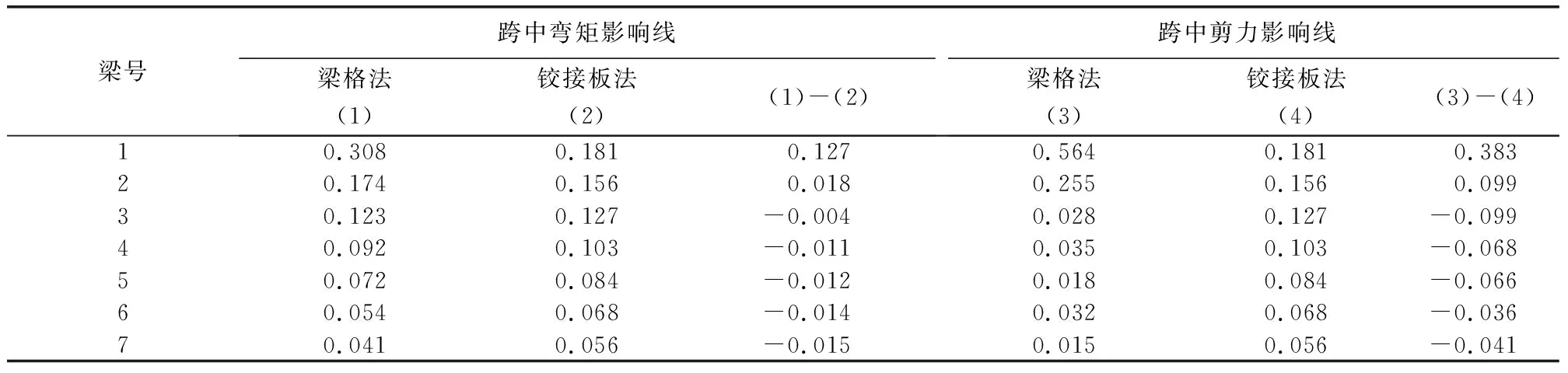
表1 单位荷载作用在1#梁跨中影响线对比

续表1

表2 单位荷载作用在4#梁跨中影响线对比

表3 单位荷载作用在8#梁跨中影响线对比

4 结 论

通过梁格法和铰接板法两种方法对跨中横向影响线计算结果的对比，可以得出以下结论。

(1)简支空心板桥整体工作时，弯矩分配梁格法和铰接板法计算结果基本一致，但直接受力板实际所受弯矩比铰接板法计算偏大约10%，协同受力板所受弯矩比铰接板法计算略小1%左右。

(2)简支空心板桥整体受力时，剪力分配采用铰接板法误差较大，直接受力板实际剪力比铰接板法计算偏大约40%，协同受力板分配剪力比铰接板法计算偏小4%左右。

(3)计算方法上的差值可能产生于铰接板法推算过程中的近似处理。首先是空心板抗扭刚度计算时的简化，其次是用正弦荷载代替集中荷载形式的车辆轮压。