具有固定转动轴线和变转动轴线3T1R并联机构构型综合

刘 伟 刘宏昭 胡旭宇

(1.西安理工大学机械与精密仪器工程学院， 西安 710048; 2.西安工程大学机电工程学院， 西安 710048)

0 引言

多模式并联机构对复杂任务具有较好的工作适应能力[1]。文献[2]在球面4R机构上增加转动副，使得球面4R机构处于折叠位形时，机构具有平面4R机构运动模式，从而设计了具有直线移动和球面滚动两种模式的移动机器人。在航天领域，具有多种运动模式的并联机构也可用来设计可展结构[3]，从而适应航天运载工具的狭小空间限制。具有多模式的并联机构可设计具有可重构性重型抓取机械手[4]。文献[5]使用平面变胞机构，设计了可根据炮筒姿态调节的自适应弹药输填装置。文献[6]利用3-RPS并联机构的两种运动模式，对其结构参数进行优化使其用于脚踝关节的康复设备。

高性能的3T1R[7-8]并联机构设计是工业应用和机构构型研究的热点。H4[9]、I4[10]、IR4[11]、Part4[12]等3T1R型并联机构在电子器件高速分拣以及食品与医药包装自动线上具有较好的应用前景[13]。文献[14-15]设计了零耦合度且解耦的3T1R并联机构。文献[16]通过两个共轴且反向等螺距螺旋副设计了具有整周回转能力的3T1R并联机构。

文献[17]使用李群理论综合了具有两种不同转动方向的3T1R并联机构。文献[18]使用有限位移旋量设计了具有可变转动轴线的3T1R并联机构。文献[19]综合了具有3T1R和2T1R运动模式的并联机构，且这两个模式的转动轴线不平行。文献[20]分析了4-CRU并联机构所具有的3种运动模式，其具有2种3T1R运动模式和1种1R2T运动模式，2种3T1R运动模式通过1R2T机构位形进行变换。

图2 具有两种固定转动轴线的球面4R机构运动模式变换Fig.2 Motion mode transformation of spherical 4R mechanism with two fixed rotation axes

目前，具有多种3T1R运动模式的并联机构构型有限，该3T1R运动模式下转动运动的轴线方向只能在两个方向上变换。具有固定转动轴线和变转动轴线3T1R运动模式的并联机构在应用于移动式调姿平台或机器人手腕具有一定的前景。本文在对具有固定转动轴线和变转动轴线的球面4R机构进行分析的基础上，综合一类具有变转动轴线和固定转动轴线的3T1R并联机构。

1 具有两种定轴线转动运动模式的球面4R机构

图1为一种球面4R机构的结构简图，图2为其三维模型图。如图2a所示球面4R机构，4个转动副轴线分别与X、Y轴重合，相邻转轴轴线夹角α12=α23=α34=α41=90°。

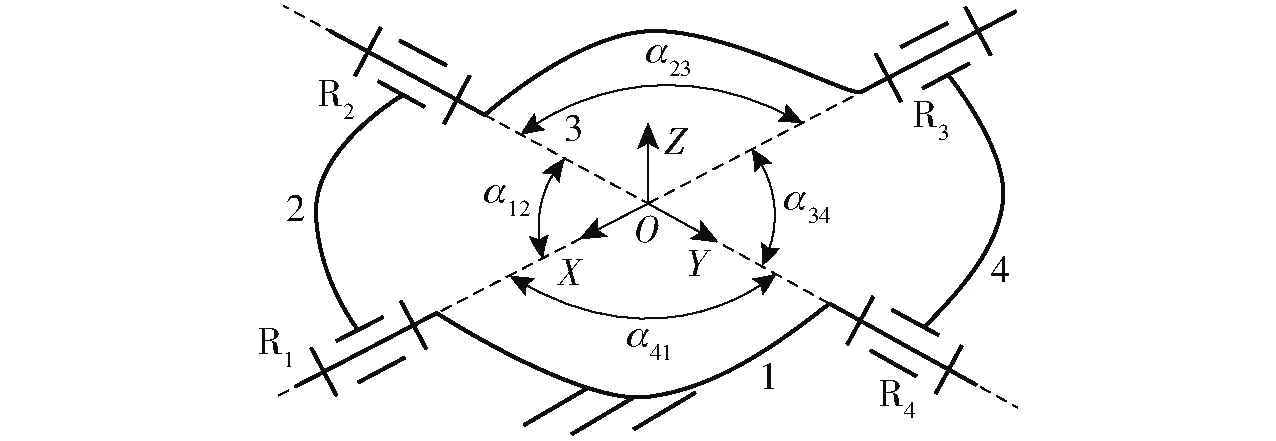
图1 两种固定转动轴线的球面4R机构简图Fig.1 Sketch of spherical 4R mechanisms with two fixed rotation axes

当机构处于图2a所示位形时，运动链R1R2和R4R3施加在连杆3上的约束旋量在坐标系OXYZ中均可表示为

(1)

在图2a所示机构位形下，由于运动链R1R2和R4R3施加在连杆3上的4个约束旋量相同，动平台上施加的约束系存在4个冗余约束，采用修正的Kutzbach-Grübler公式计算机构自由度，即

M=6(n-g-1)+∑fi+υ-ζ

(2)

式中M——机构自由度

n——机构构件总数

g——机构运动副数

fi——第i个运动副的自由度

υ——冗余约束数

ζ——局部自由度

计算得自由度为2。对连杆3上的约束系计算与其互易积为零的旋量系，可知在图2a所示位形下，连杆3可以过点O在XOY平面上的任意两条轴线做瞬时转动。然而，上述过点O在XOY平面上的转动轴线，并不全是连杆3的连续转动轴线，需要对XOY平面上的转动轴线的连续性进行判断[21-22]。转动轴线的连续性可通过建立机构运动学方程进行分析。文献[23]给出球面4R机构运动学计算式为

c1(s12Y4)+s1(s12X4)+(c12Z4-c23)=0

(3)

其中

X4=s34s4
Y4=-(s41c34+c41s34c4)
Z4=c41c34-s41s34c4

式中sij、cij——转轴i转动到j的正弦函数和余弦函数

si、ci——转轴Ri转角的正弦函数和余弦函数

将s12=s23=s34=s41=1，c12=c34=0代入式(3)得到

s1s4=0

(4)

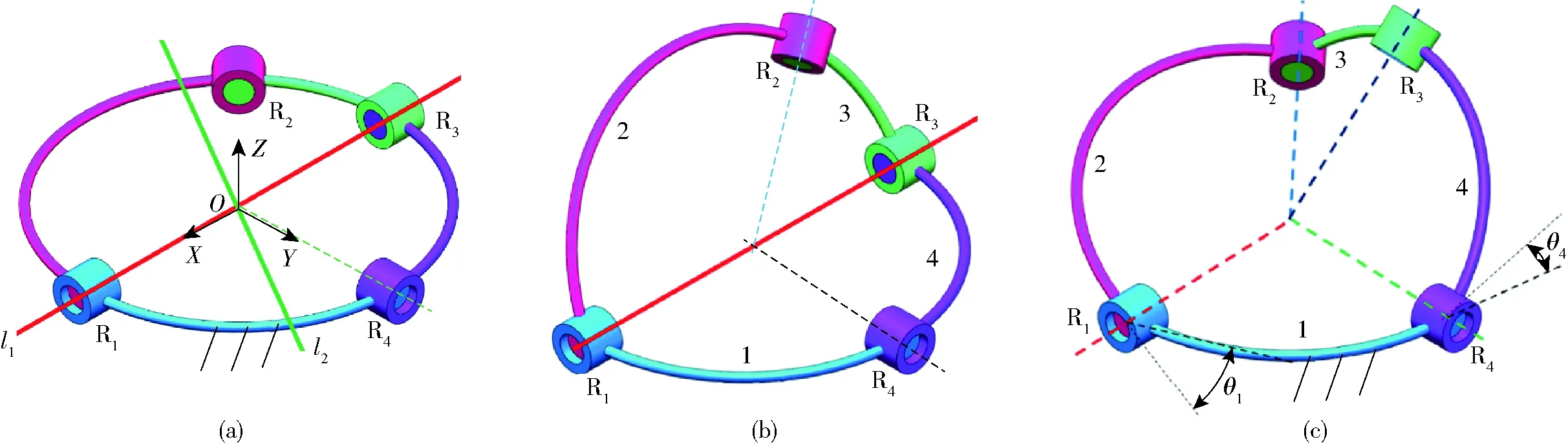
图4 具有固定转动和变转动轴线球面4R机构运动模式变换Fig.4 Motion mode transformation of spherical 4R mechanism with fixed and variable rotation axis

假设图2a中连杆3绕一般轴线l3做有限转动，R1和R4的转角都应不为零，将其代入式(4)，等式两边不相等，因而轴线l3不是连续转动轴线。由式(4)可知，当转动副R4的转角不为零时，转动副R1的转角必为零，此时机构位形如图2b所示，连杆3绕固定转动轴线l1做连续转动；当转动副R1的转角不为零时，转动副R4的转角必为零，此时机构位形如图2c所示，连杆3绕固定轴线l2做连续转动。由于机构离开图2a所示位形后，机构自由度减少为1，发生了改变，因而图2a所示机构位形下，机构具有两个自由度是瞬时的，且连杆3的两个连续转动轴线分别为l1和l2，即图2所示4R机构的连杆3具有两种运动模式，分别为沿轴线l1和l2的固定轴线转动。文献[15]利用图2所示空间4R机构的该特征，设计了具有两种3T1R运动模式并联机构。

2 具有固定转动轴线和变转动轴线两种转动运动模式的球面4R机构

当图3中空间4R机构的结构参数αij取一般值时，空间4R机构连杆的瞬时转动轴线不是固定的，而是在不断发生变化，文献[16]根据这一点设计了具有变转动轴线的3T1R并联机构。α12=α，α23=180°-α，α34=90°，α41=90°时，该空间4R球面机构简图如图3所示，取α=120°，该空间4R球面机构的三维模型图如图4所示。

图3 具有固定转动轴线和变转动轴线两种模式的球面4R机构运动简图Fig.3 Sketch of spherical 4R mechanism with two motion modes with fixed rotation axis and variable rotation axis

当机构处于图4a所示位形时，运动链R1R2和R4R3施加在连杆3上的约束旋量系在坐标系OXYZ中均与式(1)相同，因而图4a中机构有两个自由度，需要对这两个转动自由度的瞬时性和转动轴线的连续性进行判断。将s12=s23，c12=-c23，s34=s41=1，c34=c41=0，代入式(3)得到

s1s12s4-c12c4+c12=0

(5)

2.1 变转动轴线运动模式

当R4的转角不为零时，式(5)可写成

(6)

根据式(6)可知，R4的转角不为零时，R1的转角也不为零。转动副R1、R4做有限转动后，连杆3在特定位形下的瞬时转动轴线应为轴线R1与R2所在平面П1与轴线R4与R3所在平面П2的交线，该交线也是上述两平面法线的共垂线。在图4a所示位形下，当转动副R4转动有限角度θ4后，转动副R1转动有限角度θ1，平面П2的法线从图4a所示的沿Z轴方向，绕转轴R4，即Y轴转动θ4；平面П1的法线从图4a所示的沿Z轴方向，绕转轴R1，即绕X轴转动-θ1。

平面П1的法线在OXYZ坐标系中为

(7)

平面П2的法线在OXYZ坐标系中为

(8)

平面П1、П2法线的共垂线平行于向量(-c4s1，-s4c1，s4s1)T，可写成(c4s1/(s4c1)，1，-s1/c1)T。将式(6)代入平面П1、П2法线的共垂线方向向量的第3个分量得到

(9)

平面П1、П2法线的共垂线方向向量的第1个分量为

(10)

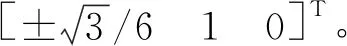
第1分量的“±”号，是由于当图4所示机构θ4一定时，θ1具有两个解，如图5所示。图5a中R4的转角θ4与图5b中R4的转角相同，机构具有两种位形。图5a所示机构位形下，轴线l2是连杆3在机构图5a位形下的瞬时连续转动轴线；图5b中轴线l′2是连杆3的瞬时转动轴线。结合连杆3的瞬时连续转动轴线向量和图5的几何分析，可知当R4的转角θ4→0时，图5所示机构有两种位形，连杆3有两个连续转动轴线l2、l′2，且由于平面П1与平面П2在空间不断连续变化，因而其交线在空间连续不断变化，即转动轴线l2、l′2在空间连续变化。

图5 θ4微小转角对应的两个球面4R机构位形图Fig.5 Two configuration diagrams of spherical 4R mechanism when θ4 had small value

2.2 固定转动轴线运动模式

转轴R4转角为0时，即s4=0，c4=1时，式(5)可写成

-c12+c12=0

(11)

此时该空间4R机构位形如图4b所示，转轴R1的转角任意选取，这种情况下，连杆3沿定轴线l1连续转动，此时连杆3具有固定转动轴线1维转动运动模式。

2.3 奇异位形

图4a所示机构处于R1、R4的转角均为零的位形。式(10)中转轴R4的转角θ4→0时，考虑到机构运动的连续性，机构从图5a所示位形下不能在R4的转角θ4→0时，运动到图5b所示位形下，结合2.1、2.2节的分析结果，可知机构在图4a所示位形下，连杆3具有两个连续转动轴线，分别为l1、l2，转动轴线l1保持固定，转动轴线l2随R4的转角θ4的变化在空间中连续变化。在图4a所示位形下，机构处于奇异位形，当锁定转动副R4的转角θ4，令其为零，控制转动副R1的转角θ1，可使得连杆3绕固定转动轴线l1连续转动；当控制转动副R4的转角θ4(且令其不等于零)，控制转动副R1的转角θ1，可使得连杆3绕变转动轴线l2连续转动。

综上所述，图4所示机构具有两种运动模式，可通过对转动副R1、R4的控制，实现机构在图4a所示变换位形下，在两种不同运动模式之间的变换。值得注意的是，该空间4R机构的两种运动模式性质不同，一种为沿固定轴线转动，该运动属于1维转动位移子群；另一种转动轴线在空间连续变化，该运动属于1维转动位移流形。利用这种空间4R球面机构所具有的运动特性，可设计具有固定转动轴线和变转动轴线两种运动模式的3T1R并联机构。

3 具有固定转动轴线和变转动轴线的两种3T1R运动模式的并联机构

由图4机构的运动特性可知，空间4R球面机构的结构参数α12=α，α23=180°-α，α34=90°，α41=90°，且α≠90°时，空间4R机构具有两种运动模式，连杆具有固定转动轴线和变转动轴线的两种1维转动运动模式。将3个沿坐标系，移动方向正交的移动副串联后，连接图4所示机构的连杆1后，连杆3所具有的运动可用位移流形表示为

{TX}{TY}{TZ}({R(X)}∪{R(v)})=
{TX}{TY}{TZ}{R(X)}∪{TX}{TY}{TZ}{R(v)}

(12)

式中 {R(X)}——1维转动位移子群[24]，转轴平行于X轴

{TX}、{TY}、{TZ}——沿坐标轴的1维移动子群

v——可变的转动轴线，这种特殊的转动运动并不属于12种位移子群

{R(v)}——1维转动位移流形

{TX}{TY}{TZ}{R(v)}不属于12种位移子群，代表4维位移流形。式(12)中的({R(X)}∪{R(v)})表示两种运动模式的并集，根据产生这种运动的生成元，可写成

({R(X)}∪{R(v)})=
{R(X)}{R(u)}∩{R(Y)}{R(X)}

(13)

式(13)中{R(X)}{R(u)}对应的生成元为图4的支链R1R2，式(13)中{R(Y)}{R(X)}对应的生成元为图4中的支链R4R3，结合式(12)，得到

{TX}{TY}{TZ}({R(X)}∪{R(v)})=
{TX}{TY}{TZ}({R(X)}{R(u)}∩
{R(Y)}{R(X)})=
{TX}{TY}{TZ}{R(X)}{R(u)}∩
{TX}{TY}{TZ}{R(Y)}{R(X)}

(14)

由于两种3T1R运动模式都具有4个自由度，使用式(14)中位移流形{TX}{TY}{TZ}{R(X)}{R(u)}、{TX}{TY}{TZ}{R(Y)}{R(X)}对应的运动链作为并联机构的两条支链，再加上2个与其结构相同的并联支链后，支链末端的运动求交，运动不会发生改变。支链1的结构为ZPYPXPXRuR，支链1与支链3的机构相同，令向量X转到u的转角为α，支链2的结构为YPXPZPYRXR，支链2与支链4的机构相同，机构的结构简图如图6所示。文献[25]根据移动副和转动副的数目列举了PPPRR类型的运动链。可选取RRRRR支链进行建模，其结构简图如图7所示。运动链B1A1的结构为YRYRYRuRuR。旋转轴R13和旋转轴R14之间的角度为60°。运动链B1A1的结构与运动链B3A3的结构相同。运动链B2A2的结构为XRXRXRYRYR。运动链B2A2的结构与运动链B4A4的结构相同。运动链3对动平台施加的约束与运动链1对动平台施加的约束相同。运动链4对动平台施加的约束与运动链2对动平台施加的约束相同。

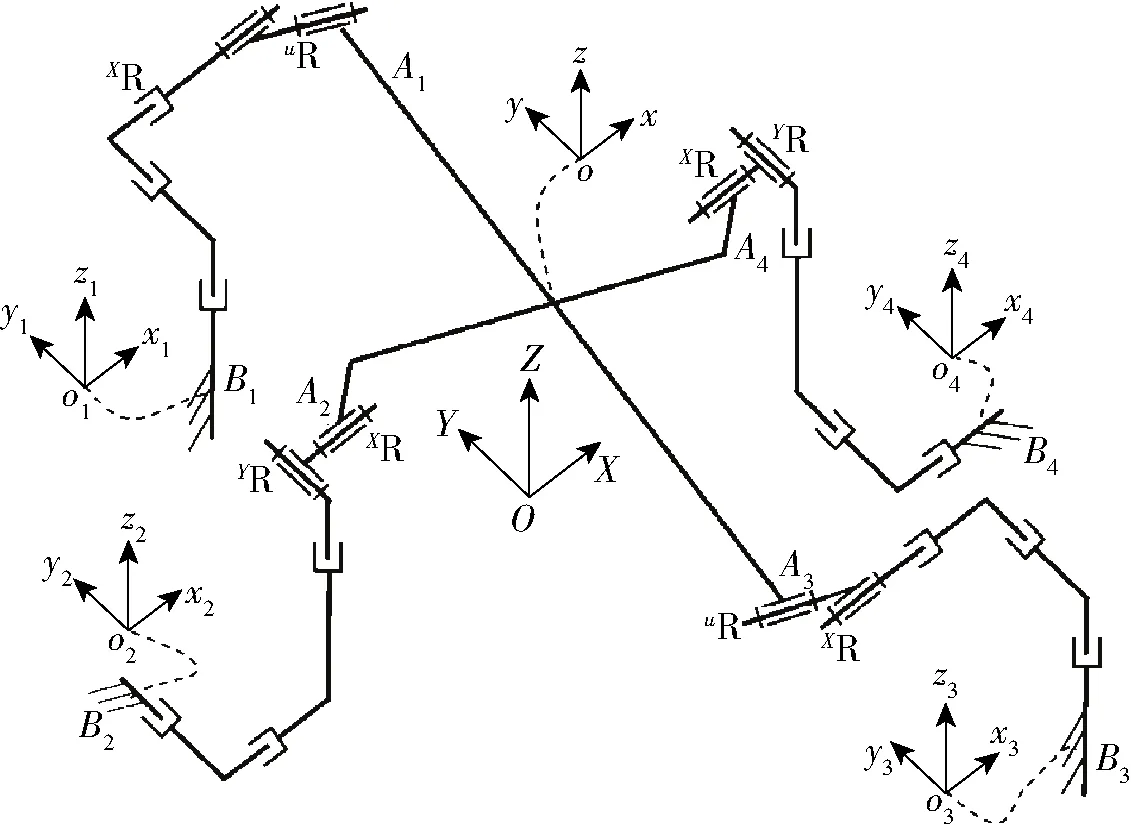
图6 具有固定转动轴线和变转动轴线的3T1R并联机构简图Fig.6 Sketch of 3T1R parallel mechanism with fixed and variable rotation axis

图7 不含有被动副的具有固定转动轴线和变转动轴线的3T1R并联机构简图Fig.7 Sketch of 3T1R parallel mechanism with fixed andvariable rotation axis without passive moving pair

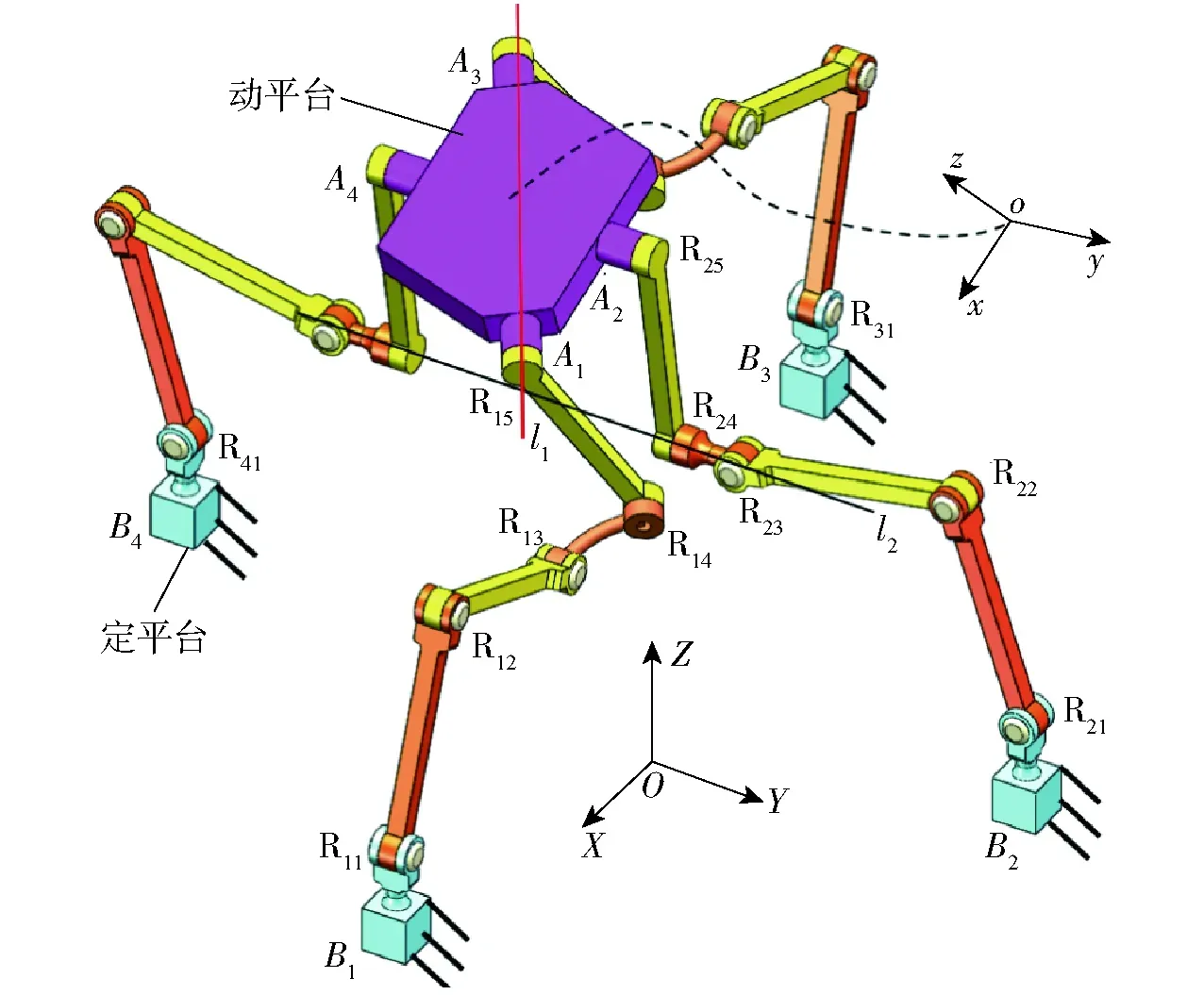
图8 定轴线3T1R运动模式Fig.8 Fixed axis 3T1R motion mode

3.1 固定转动轴线3T1R运动模式

3.1.1自由度分析

如图8所示支链B1A1的结构为YRYRYRuRuR。转轴R13和转轴R14之间的角度为60°。运动链B1A1的结构与运动链B3A3的结构相同。运动链B2A2的结构为XRXRXRYRYR。运动链B2A2的结构与运动链B4A4的结构相同。运动链3对动平台施加的约束与运动链1对移动平台施加的约束相同。运动链4对动平台施加的约束与运动链2对动平台施加的约束相同。在图8中，运动链B1A1、B2A2施加在动平台上的约束旋量可以在固定坐标系OXYZ中表示为

(15)

支链1与支链3，支链2与支链4施加在动平台上的约束相同，在机构的一般位形下，动平台上施加的约束系存在冗余约束，υ=2，采用修正的Kutzbach-Grübler公式计算机构的自由度为4。

结合动平台上的约束，对其求解互易积，可知机构在图8所示位形下，具有3T1R运动模式，转动轴线平行于Y轴。根据文献[26]中的方法判定运动模式是否瞬时，对应每一个自由度和其性质依次给出相对起始位型的一个足够小的有限位移量。可以验证该3T1R运动模式是全周的。

3.1.2固定转动轴线3T1R模式驱动副选择合理性分析

选择转动副R11、R21、R31和R41作为驱动副。当驱动副R11、R21、R31和R41在图8中被锁定时，施加到动平台的驱动力旋量为

(16)

锁定4个驱动副后，该机构具有0自由度。在图8所示的机构位形下，所选择的4个驱动副可实现机构在固定转动轴线3T1R运动模式下的控制。

3.2 3T1R运动模式变换位形

3.2.1机构自由度分析

机构在图8所示位形绕平行于Y轴的轴线转动后，机构处于图9所示机构位形，此位形下，4条支链中的转动副轴线均平行于OXY平面。运动链1、2施加在动平台上的约束旋量可以在固定坐标系OXYZ中表示为

(17)

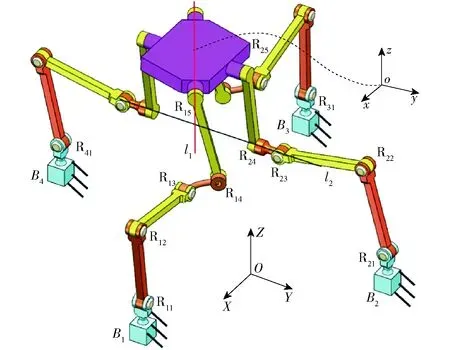
图9 运动模式变换位形Fig.9 Motion mode transformation configuration

机构具有5个自由度，结合动平台上的约束，对其求解互易积，可知机构在图9所示位形下，具有3T2R运动。根据3.1节的分析可知，当机构从图9所示位形绕平行于Y轴的轴线转动后，机构进入固定转动轴线3T1R运动模式，因而图9所示机构具有的3T2R运动是瞬时的。

3.2.2驱动副选择的合理性分析

在图9所示机构位形下，驱动副R11、R21、R31和R41被锁定后，施加到动平台的驱动力旋量为

(18)

由式(17)、(18)组成的旋量系可知，在图9的机构位形下，旋量系中的8个旋量是线性相关的。施加在移动平台上的约束旋量系中有3个冗余约束υ=3，计算机构的自由度为1。

锁定机构4个驱动副后，该机构有1个自由度。在图9所示的机构位形下，所选的4个驱动副无法实现机构运动模式变换。因而需要增加1个辅助驱动副，来实现机构运动模式的变换。选择转动副R12作为辅助驱动副。锁定该驱动副后，作用在动平台上的驱动力旋量为

(19)

由式(17)～(19)组成的旋量系可知，在机构的运动模式变换位形下，该9个旋量线性相关。在动平台上作用的约束旋量系中有3个冗余约束υ=3，计算机构的自由度为0。

锁定4个驱动副和1个辅助驱动副后，该机构自由度为0。在图9所示的配置下，4个驱动副和1个辅助驱动副可以实现机构3T2R瞬时自由度位形下的控制。

3.3 变转动轴线3T1R运动模式

3.3.1机构自由度分析

控制图9中4个驱动副和1个辅助驱动副，使得机构处于图10所示机构位形，支链1、2施加在动平台上的约束旋量，在定坐标系OXYZ中可表示为

(20)

图10 变轴线3T1R运动模式Fig.10 Variable axis 3T1R motion mode

由于支链1与支链3，支链2与支链4施加在动平台上的约束相同，在机构的一般位形下，动平台上施加的约束系存在冗余约束，υ=2，采用修正的Kutzbach-Grübler公式计算机构自由度为4。

3.3.2驱动副选择的合理性分析

当驱动副R11、R21、R31和R41在图10中被锁定时，4个支链施加到动平台上的驱动力旋量为

(21)

由式(20)、(21)组成的旋量系可知，在机构的一般构型下，旋量系中的8个旋量在变转动轴线的3T1R运动模式下线性相关。施加在动平台上的约束旋量系中有两个冗余约束υ=2，计算机构的自由度为0。

锁定4个驱动副后，该机构自由度为0。在图10所示机构位形下，选择的4个驱动副可以实现机构在变转动轴线3T1R运动模式下机构的控制。

综上所述，图10所示的机构具有固定转动轴线和变转动轴线的两种3T1R运动模式。可以使用4个驱动副来控制机构的这两种运动模式。当机构运动模式改变时，机构支链中需要增加一个辅助驱动副。辅助驱动副只在机构运动模式变换位形下工作。

4 结论

(1)通过分析空间4R球面机构的一般运动学方程，对一种具有特殊结构参数的空间4R球面机构具有的运动模式进行了讨论，结果表明该空间球面4R机构的连杆具有两种运动模式，其具有固定转动轴线和变转动轴线两种转动运动模式。

(2)使用位移流形理论对具有固定转动轴线和变转动轴线两种运动模式的3T1R并联机构进行了综合，在机构运动模式变换的不同位形下，进行了机构自由度和驱动副选取合理性的验证，结果表明该类机构能实现两种模式的运动，在机构运动模式变换位形下，使用辅助驱动副可以实现机构运动模式变换。