叶轮出口后加装双层流道结构的轴流泵外特性研究

周勇胜 陈 斌 张德胜 张 华 杨 陈

(1.合肥工业大学机械工程学院， 合肥 230009； 2.南京信息工程大学环境科学与工程学院， 南京 210044；3.江苏大学流体机械工程技术研究中心， 镇江 212013； 4.扬州大学水利科学与工程学院， 扬州 225009)

0 引言

轴流泵在农业、水利工程中广泛使用。采用轴流结构形式，可以提高比转数，有利于增加流量。轴流泵高效率运行区流量范围较小，在最佳工况流量点两侧效率急剧下降[1]。因进水水位变化等原因，流量变化范围不确定，对轴流泵有根据流量变化调节工况的需求。当发生小流量工况时，因流量-扬程曲线存在马鞍形不稳定区域，会出现同一扬程有两个流量的现象，轴流泵易发生旋转失速，产生激烈的振动，影响机组安全[2-3]。实际工程中轴流泵机组被禁止运行在此流量范围。研究轴流泵全流量下的内部流场特性，提出改善方法，拓宽轴流泵的使用范围，具有实际意义。

众多学者对轴流泵叶轮出口区域和叶顶间隙附近的相关流动与不稳定流量区域的改善方法进行了研究。文献[4-6]用数值计算法研究了叶轮出口尾迹区非定常压力脉动。文献[7-8]采用数值计算与PIV试验研究相结合的手段对叶轮进口附近流场进行了研究。文献[9-10]分析了不同叶顶间隙大小对叶顶泄漏涡的影响，并研究了叶顶间隙形状对叶顶空化涡的影响。文献[11]对叶顶泄漏涡形成演化机理与空化条件进行了研究。文献[12-15]利用高速摄影及油膜试验相结合的手段，发现叶轮失速的起始点正是扬程曲线出现拐点的位置。除了内部流动机理的研究以外，部分学者还提出了改善轴流泵不稳定区的措施。文献[16]提出采用J型沟槽的方式来抑制旋转机械不稳定流动，但该方法会造成在J型沟槽进口端产生严重的汽蚀。文献[17]采用双喇叭进口的结构有效抑制了轴流泵的不稳定区域。文献[18]则采用了进水管壁面开槽的办法消除驼峰。文献[19]研究了不同叶片安放角对轴流泵驼峰区的影响，而文献[20]则研究了增设前置导叶对消除马鞍形的影响。以上方法均选择了针对叶轮进口前区域或叶轮本体进行研究。对于流动分离，文献[21]基于OpenFOAM平台用数值法分析了在雷诺数3 900的情况下不同长度的来流侧隔板对圆柱钝体绕流流场的影响。文献[22]对导叶式离心泵径向导叶内流场进行了试验研究，发现大流量时导叶压力面发生了流动分离，并研究了引入涡流的方式进行控制。

本文以350ZQB-125型电机内置式轴流泵为模型进行研究，基于轴流泵固有的流动特性，选择叶轮出口边后的区域作为主要研究区域，在近轮毂侧从紧邻叶轮出口边起至后导叶体内增加双层流道结构，通过采用定常与非定常数值计算结合开式试验台外特性试验对比的研究手段，分析不同几何尺寸的双层流道对轴流泵的外特性与流动损失的影响。

1 研究方法

1.1 水力模型与试验台试验

轴流泵的参数为：设计流量Qd为1 100 m3/h，设计扬程Hd=4.2 m，转速n=1 450 r/min。叶轮外径D2为300 mm。叶轮叶片数3片，导叶叶片数5片。

外特性试验采用图1所示的开式试验台进行。管路系统内的流动方向为从左至右，此试验台用于潜水泵在实际淹没状态下的抽水输送测试。试验按ISO 9906:2012标准[23]施行。流量、扬程、效率测试精度分别控制在±2.0%、±1.5%、±2.9%范围内。此精度可以满足试验台试验与数值计算两种方法所获外特性数据的对比验证。

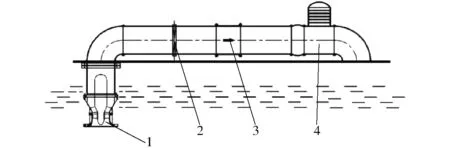
图1 开式试验台示意图Fig.1 Schematic diagram of open type test rig1.试验泵段 2.压力传感器 3.流量计 4.出口闸阀

试验管路系统主要由泵段、电磁流量计、压力传感器、扭矩仪以及出口闸阀等组成，通过线缆连接至自动监测系统和测试系统控制台，可以实现试验数据的自动采集以及运行中流量的智能化控制，并能够避免人工读数造成的观测误差。外特性试验过程中，每调节一次阀门开度后，系统稳定运行1 min以上再进行数据采集。试验重复3次，每次获得的性能曲线非常吻合，本试验台具有良好的重复性。

轴流泵的流量-扬程曲线存在不稳定区域，从设计工况开始，随着流量的减小达到一定程度，叶轮内部流场出现旋转失速，导致扬程随着流量的减小而下降，机组伴随激烈的振动，该现象一般会出现在0.7Qd左右。试验中为避免机组振动导致意外，外特性试验的采集范围为0.8Qd～1.2Qd。

1.2 数值计算

图2为轴流泵计算域的水体模型，主要包括进水段、叶轮水体、导叶水体、出水段。考虑到水体在流道内的充分发展，将进口断面设在来流方向上游2D2处。出水方式与试验台管路保持一致，并设有90°弯管，计算模型的出口断面延伸至实际出水口的取压孔处。

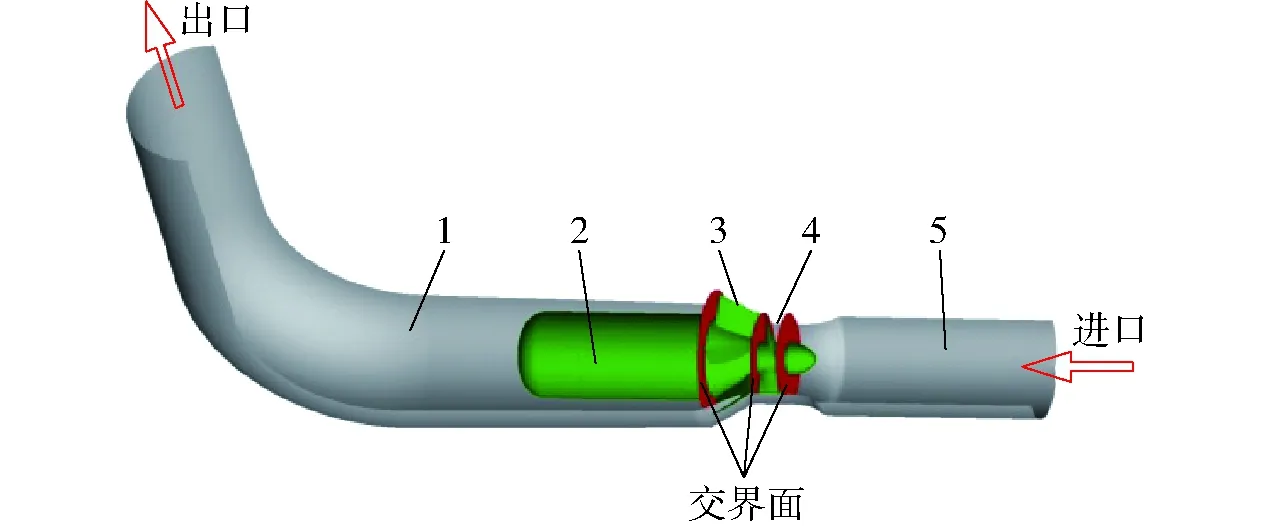
图2 水体计算域划分Fig.2 Domains setup for numerical simulation1.出水段 2.电机室 3.导叶水体 4.叶轮水体 5.进水段

图2中灰色部分为泵体与管道的部分壁面。此泵的结构特点是电机内置在流道中，因此导叶的流道需要向外偏斜以容纳电机室，从进水端至导叶出口的流道有直道—斜道—直道的变化。此结构节省工程造价，安装方便，特别适合水位涨落大的地区。

网格质量对内部流场求解和空化状态描述有至关重要的作用，为保证计算精度，在ICEM CFD 15.0软件中对整个计算域采用了六面体结构化网格划分。网格离散了从进口测压点端面至出口测压点端面间的水体空间。其中叶轮水体包含了叶顶间隙，间隙内在径向方向设置10层网格节点。在其他壁面处，通过对相应关联块的节点分布设置，对网格作了加密处理。本计算中模型壁面处y+<60，其中y+表示无量纲壁面距离。叶轮与导叶水体的网格情况如图3所示。

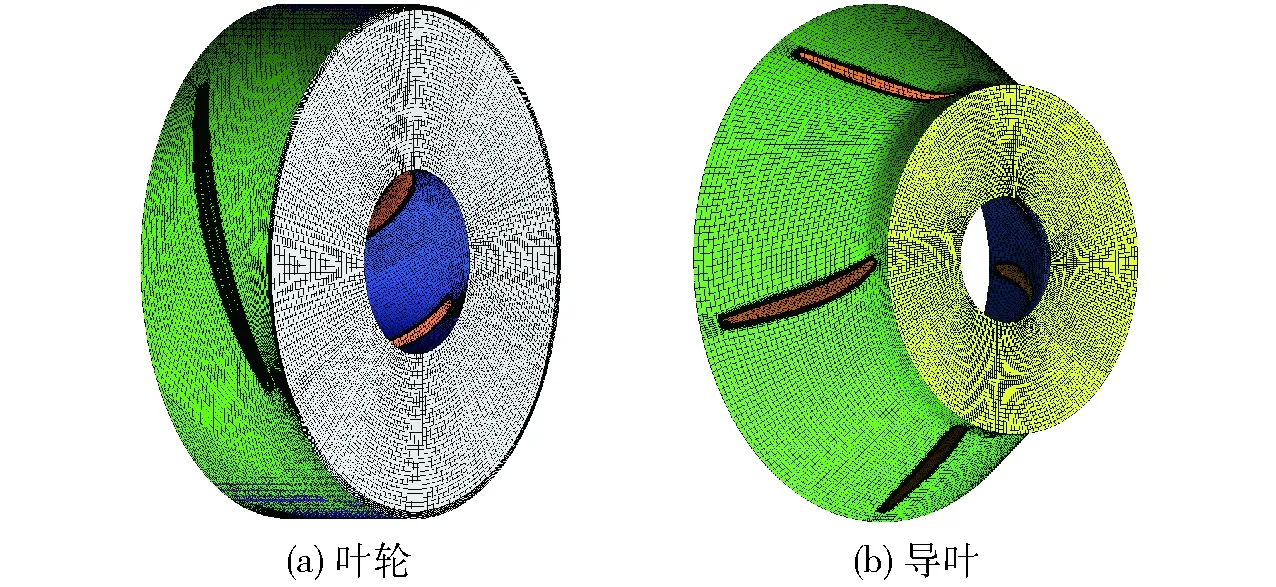
图3 叶轮与导叶的水体网格Fig.3 Water body meshes of impeller and guide vane

通过改变网格尺寸的全局设置及关联块上相应边的控制节点数等方法来调整最终生成的网格总数，以扬程H的波动作为监测值进行了网格无关性验证。当模型的网格总数达到4.4×106之后，扬程的波动甚微，因此选定了这组网格作为数值计算的空间离散数据形式。表 1为该组网格各切分区域的质量情况与节点数量。

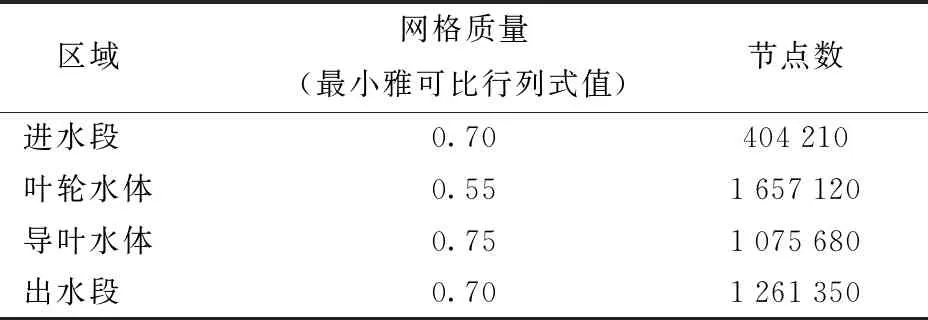
表1 各水体计算域的网格信息Tab.1 Mesh information of every domain

以ANSYS CFX 15.0商用软件作为数值计算平台，采用相对旋转坐标系方法，首先对全流场进行了单相定常数值计算。以雷诺时均方程为控制方程，采用SSTk-ω湍流模型，该模型综合了自由流中的k-ε模型和近壁区计算的k-ω模型的优点，兼顾了壁面区域的低雷诺数流动，对预测存在逆压梯度的分离流动和轴流泵的叶顶间隙流动具有独特的优势[24]。

介质设定为不可压缩流体，设置进口属性为均匀来流，给定进口速度大小为vin，设置参数时定义了vin与体积流量Qv，vin由Qv输入值按表达式计算，设置def文件时，输入拟计算的体积流量即可完成设置。出口属性为自由出流，给定静压。对于数值计算中的近壁区域，均设为非滑移壁面，选择scalable壁面函数进行求解计算。除了叶轮区域为旋转区域外其余均为固定区域。区域间的动静交界面模型采用stage连接方式。数值仿真的收敛精度设置为10-4。

在定常计算的结果基础上，选择流量900 m3/h作了非定常计算，对流道中的取样点作了压力脉动分析。非定常计算以叶轮每转过3°为一个时间步，计算了6圈，又取后3圈的结果进行了频域分析，对压力计算均值。

2 试验与数值计算的结果对比

2.1 外特性结果对比

图4为数值计算与试验台试验的外特性结果对比。试验中最优工况点的流量Qopt为1 041.47 m3/h，扬程Hopt为4.46 m，效率ηopt为66.56%。数值计算中统计了800～1 200 m3/h间隔100 m3/h的5个流量下的数据。根据试验数据按线性内插计算出的扬程相对误差分别为：-2.2%、-2.2%、-3.0%、-5.3%和-11.4%。对于大流量工况，实际泵运行过程中存在汽蚀现象，而数值计算中并未启用空化模型。小流量工况下，数值计算与试验获得的扬程误差较小。试验获得的功率不仅包括水功率，还包括机械损失等引起的功率消耗，因此不对效率作误差分析。从流量-扬程和流量-效率曲线的走势来看，数值计算与试验台试验的结果基本一致，可以验证本文所用数值计算的准确性是可以接受的。

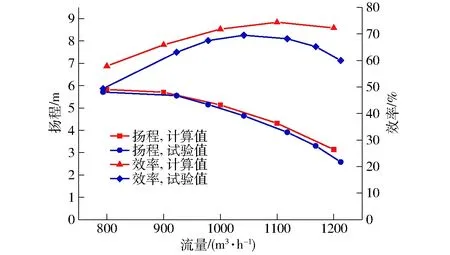
图4 试验台与数值计算的流量-扬程、流量-效率曲线对比Fig.4 External characteristics comparison between numerical simulation and test rig experiment

2.2 流场分析

选择最优工况附近的3个流量1 200、1 000、800 m3/h进行了流场分析，本模型的进口流动方向为Z轴正向，观察平面选择了YZ面，观察区域为叶轮出口后、导叶区和部分电机室外部流道。

速度矢量的分布如图5所示。可见：流量1 200 m3/h时，此区域内整体流动分布比较平均，与流道平行，流速较大。此潜水轴流泵不同于导叶轮毂为圆柱型的传统轴伸式轴流泵，因电机内置，导叶轮毂内含电机室而呈锥型。叶轮后流道有两个转角造成了过流断面面积变化，导叶体与出水管联接处为其中之一的钝角转角。从导叶流出时截面积增加，为扩散式流动，因边界层流动分离形成了一个回流涡旋。此涡旋阻碍了导叶出口后管道内壁侧的流动，使得流速减小，流动随着涡旋向轮毂侧偏转。流量1 000 m3/h时，叶轮出口边后可见明显由轮毂向轮缘侧速度偏转，导叶流道内外圈流速快，近导叶轮毂内圈流速慢，存在速度梯度。因平均流速小于1 200 m3/h时的情况，导叶出口后的涡旋受主流的牵连运动小，因此转角涡旋的影响区域反而大于1 200 m3/h时的情况。当流量继续下降到800 m3/h时，仍是以流道外圈为主流通道，叶轮出口边处轮毂向轮缘侧的速度偏转更加明显。因流速下降，转角处的流动分离消失，涡旋也消失，但流道内圈因流量不足，速度梯度影响大，使得在流体粘滞力的作用下流道中出现大面积的涡旋，阻塞了流道，使扬程下降。

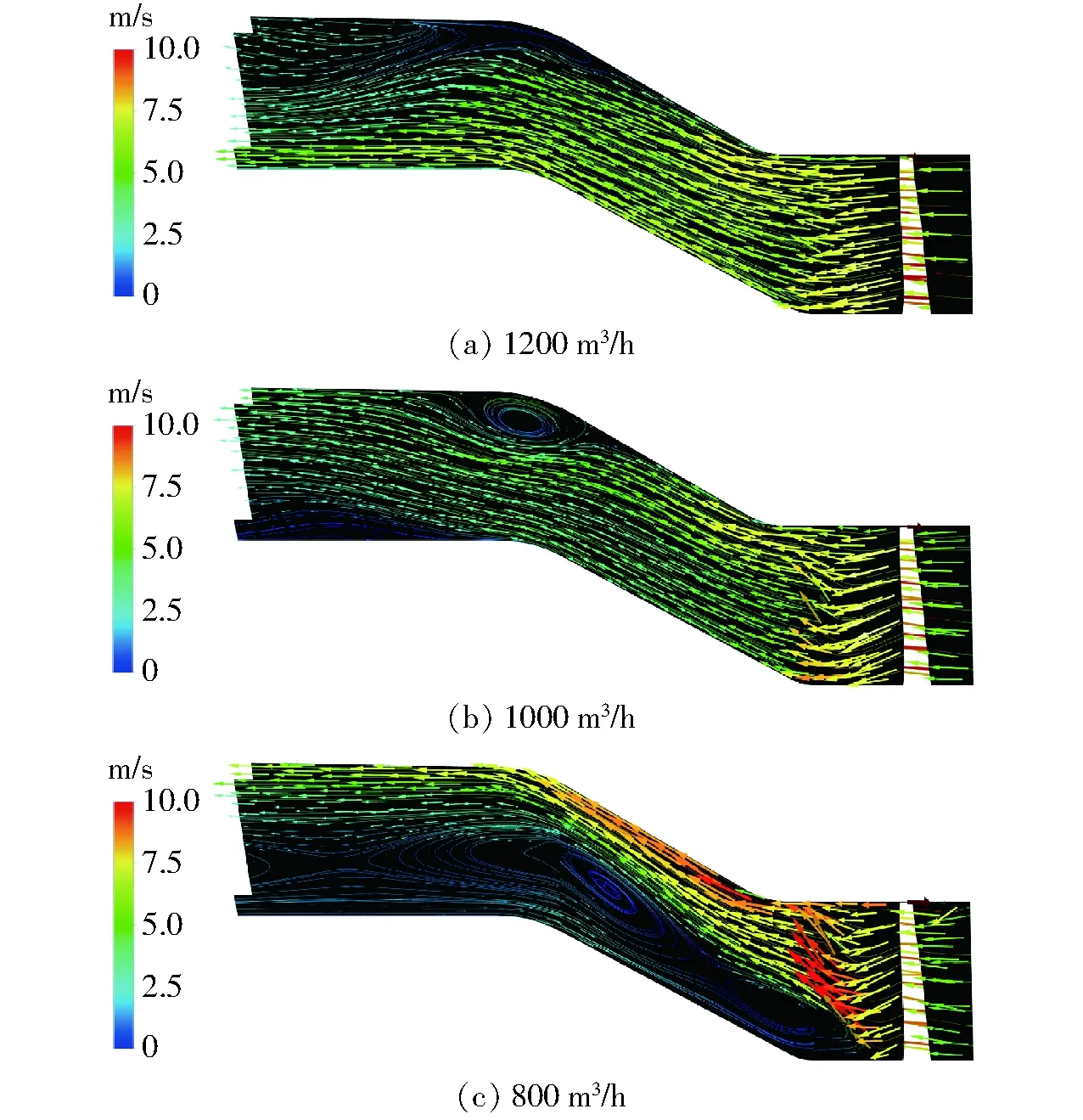
图5 叶轮出口后区域的速度矢量与流线图Fig.5 Velocity vectors and streamlines at area after impeller

结合YZ轴面上流线分布情况(图5中蓝色细线部分)，清晰可见小流量时叶轮出口边后轮毂侧出现的涡旋和大流量时导叶出口后管道内壁侧因边界层分离导致的主流向轮毂侧偏转。

其他角度轴面上的流动与YZ面的情况类似。

3 小流量工况扬程预测与流场分析

3.1 全流量区间扬程预测

以相同的数值计算方法，对轴流泵的全流量范围400～1 400 m3/h进行了扬程预测。在900～1 400 m3/h范围内，随着流量的减小，扬程逐渐增加，此区间的数值计算精度已被试验所验证。在700～900 m3/h范围内，扬程随着流量的减小不再减小，由于可能发生激烈的振动，轴流泵机组通常被禁止运行在该流量范围。在该范围内，轴流泵内部流场极为复杂，数值计算的精度也会相应降低。当流量进一步减小至小于700 m3/h后，随着流量的减小，扬程再次快速增加。

叶轮出口边后的流场在流量500、700、900 m3/h的情况如图6所示。可以清楚看到随着流量减小，出口边后轮毂侧的回流范围与涡旋区域均有增加。流量700 m3/h以下工况时，导叶内涡旋的影响区域已占据流道径向尺寸1/2以上，主流被推向管道外侧的狭长区域，泵的效率下降。

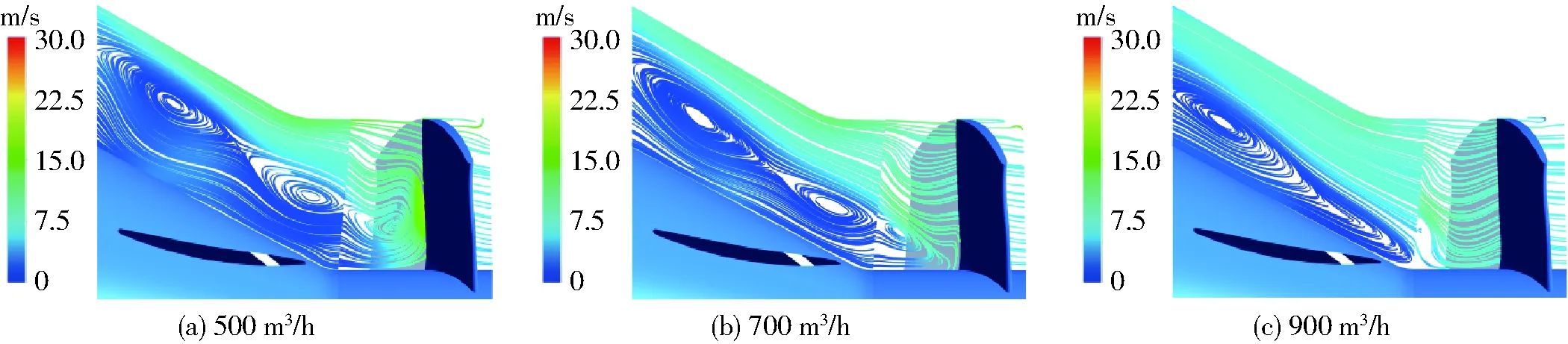
图6 小流量时叶轮出口后流场变化Fig.6 Streamlines after impeller at low flow rates

3.2 流动与改善方法

在叶轮出口边，不同半径处叶片相对流动角不同，当流量减小时，绝对速度的轴面分量是相同的，同时减少，但绝对速度的圆周分量原理变化幅度不同，形成的差别较大，造成了不同半径处扬程的差别，出口压力也不同，水流从高压处向低压处流动，液流涌向外缘侧，轮毂侧出现空位回流区，使轴面流线如图7a中红线所示。速度三角形分析如图7b所示。

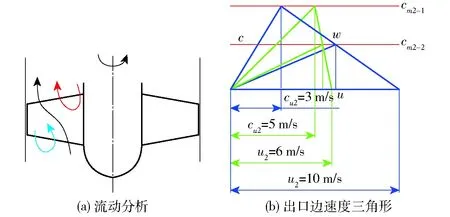
图7 流量下降时叶轮进出口处流动情况与速度三角形分析Fig.7 Analysis of flow around impeller and velocity triangle when flow rate drops

图7b中蓝色线条代表轮缘处出口速度三角形，绿色为轮毂处出口速度三角形，两处的牵连速度u2因所处半径不同而不同。在设计工况下，绝对速度轴面分量为cm2-1，此时，两处流线上扬程是相等的，为设计扬程。因轴流泵通常为法向进口，进口绝对速度的圆周分量cu1=0，欧拉方程简化为：H=u2cu2/g，其中cu2为出口的绝对速度圆周分量，g为重力加速度。按图7中的比例，轮缘处u2=10 m/s，cu2=3 m/s，轮毂处，u2=6 m/s，cu2=5 m/s，所以两处扬程是相等的(以上数值为示意用)。当流量减小时，绝对速度的轴面分量cm2相应减小，假定变为cm2-2，由于叶片角没有变，速度三角形顶点将沿着相对速度方向向下移动[25]。这时可以看到，轮缘处由于相对流动角β2小，顶点在圆周方向移动距离很大，cu2增大了一倍多；而在轮毂处，cu2仅增加了约10%。所以这将造成两处扬程的差别，出口压力也不同，造成了水流从高压处向低压处流动，使轴面流线成为图7a中红色所示的形状。

这必然引起流动损失，造成扬程降低。这是流量减小时，扬程先增加然后降低的原因。如果回流继续发展，将造成水流多次流出又流入叶轮，多次从叶轮获得能量，扬程又呈增加趋势，流量-扬程曲线表现出同一扬程时可对应多个流量的马鞍形不稳定流量区域。

轴流泵叶轮因安全运行的要求，在叶顶处必然存在与转轮室内壁的间隙，叶轮进口边轮缘侧因压力面与吸力面压差形成叶顶泄漏。并且随着流量的减小，泄漏涡强度不断加大，占据主流的面积不断增加，从而破坏了进口流场，形成进口边前的流动阻碍。泄漏流在主流的挟带下又折回沿主流方向运动，如图7a中蓝线所示。关于叶轮进口前双进口结构对外特性的研究见文献[26]。

此模型流道的导叶出口后流动为扩散流动，当流动分离条件满足时，会在管道内壁侧发生边界层分离，流道出现涡旋，影响主流的运动。通常控制流动分离的方法有：控制主流的减速方式、用旁路流动或注入流动的方法消除边界层、把层流边界层变成湍流边界层、分隔流道等。对于此模型，分隔流道的办法可以起到兼顾均衡出口边不同半径处cu2值和减轻下游流动分离的作用。

4 双层流道结构

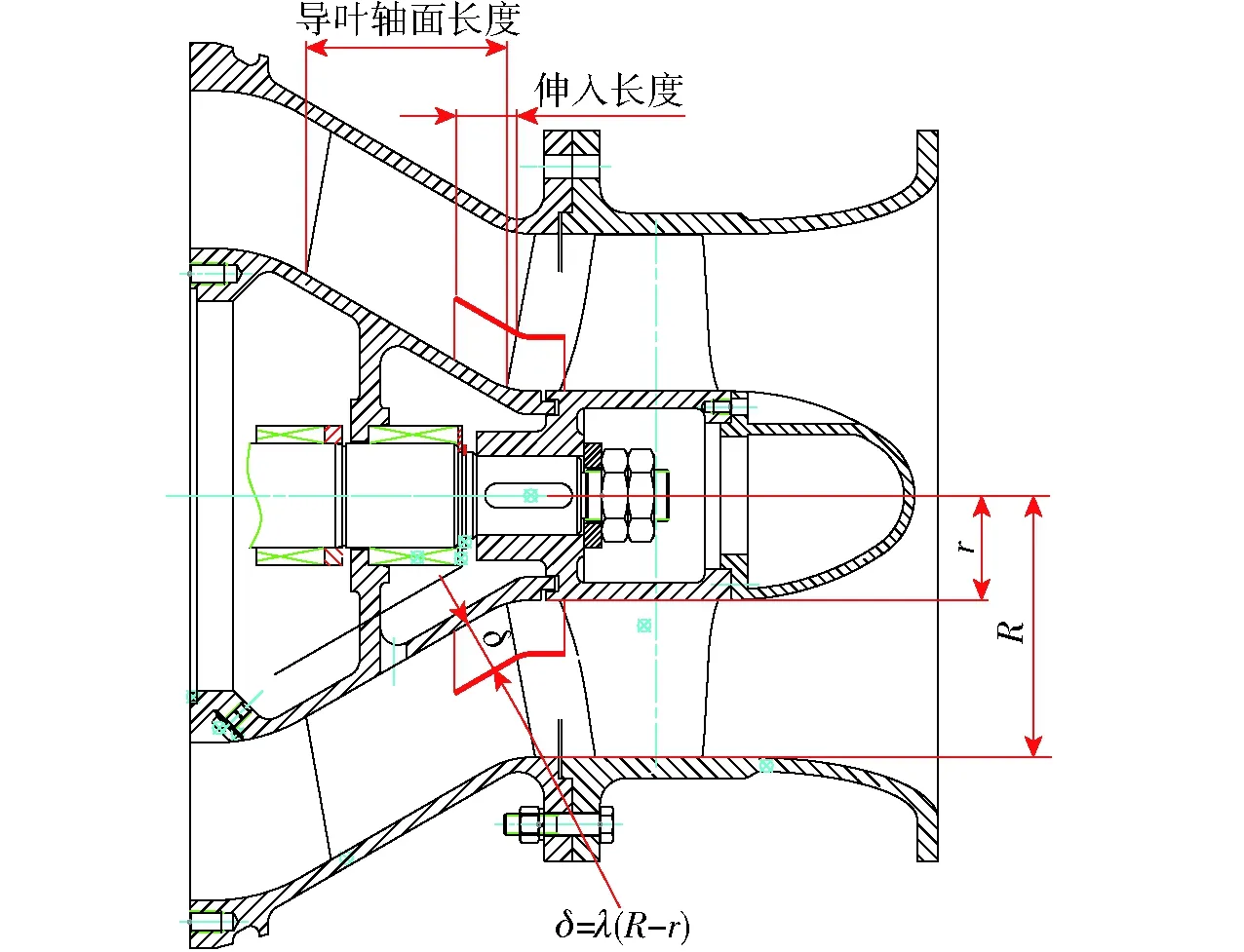
图8 双层流道结构示意图Fig.8 Schematic of double-layer flow passage structure

本文设计加装的双层流道结构如下：从叶轮出口边轴面投影处往下游5 mm处开始，由轮毂体向外偏置距离δ，厚度取为2 mm，旋转一周后形成一个回转型的内筒，如图8所示。出于效率的考虑，筒体伸入导叶体长度设为导叶轴面距离的1/4。取δ=λ(R-r)，本文中λ选取3个挡值，分别为1/5、1/4与1/3。选取的原因是根据前文观察的无内筒普通泵流场情况，隔板布置在这些位置经过了涡旋中心，可以起到减少流体层间的流动干扰作用。

4.1 对叶轮出口后流场的影响

与普通泵小流量时的流场相比，图9中流线显示出加装了双层流道后，叶轮出口边后区域的流动变化情况，可见筒型隔板对回流涡旋的明显抑制作用，在小流量500～900 m3/h时，隔板间内流道流线平直，轮毂侧靠近叶轮出口边的涡旋明显受到抑制，区域变小。当接近设计工况时，内流道的通流能力增加。

大流量时，导叶出口后过流断面面积增加的扩散流动处易形成边界层流动分离。图10为大流量时导叶体后出水管内的流动情况。在流量1 200 m3/h时，导叶出口后管道内壁侧的涡旋消失，流动在整个流道中更加平顺。流量1 000 m3/h时，明显可见原转角处的边界层流动分离现象在加装内筒后得到了抑制，导叶流道中的通流速度也有所增加，通流能力大为提升，解释了大流量时扬程提升的原因。

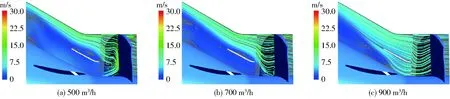
图9 λ=1/3时叶轮出口后的流场Fig.9 Flow field after impeller at λ=1/3

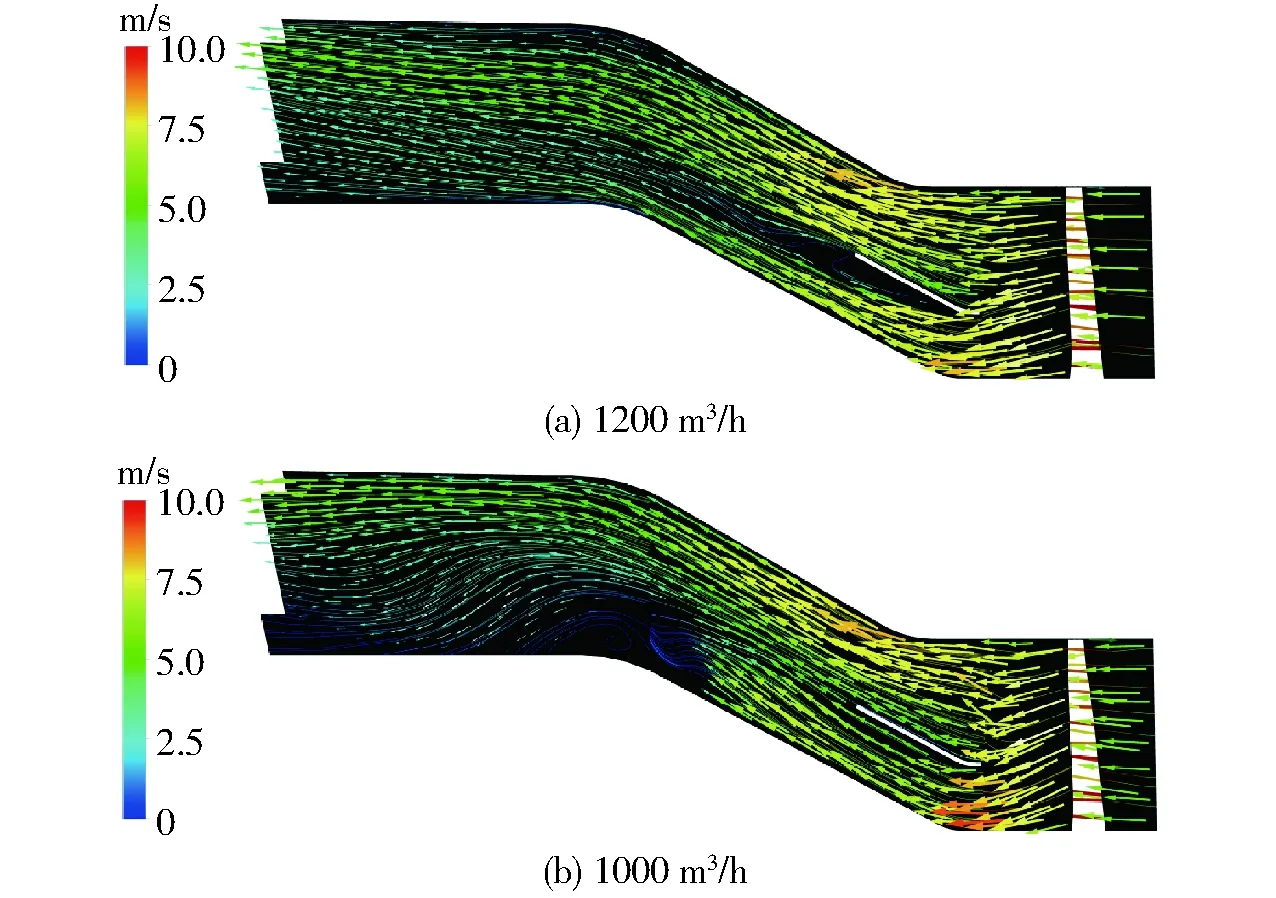
图10 大流量工况时λ=1/3双层流道泵叶轮后区域的速度矢量与流线图Fig.10 Velocity vectors and streamlines at area after impeller of λ=1/3 double-layer structured pump at large flow rates

通过以上分析，双层流道可以改善小流量工况流态，它将不同半径处的流动分隔，减少了轮毂侧回流引起的相互影响，从而部分抑制了回流，减少了流动损失增加了扬程。在大流量时，内筒对后续流动起到了分隔、稳流作用，破坏了边界层分离条件，扩大了主流范围，从而显著提升了扬程与效率。

4.2 非定常计算与压力脉动

在流场中如图11所示的3处过流断面位置设置了取样线，第1条线位于叶轮出口后，通过双层流道中部位置；第2条位于双层流道出口后、导叶体中部；第3条线位于导叶出口后贯穿流道的转角处。每条线上自外缘向轮毂方向均布了5个监测点，共计15个压力监测点。

图11 压力监测点设置示意图Fig.11 Schematic diagram of pressure monitoring points setup

非定常计算选择的流量为900 m3/h，约0.8Qd，此流量处于马鞍区。以定常计算结果为初始值，叶轮每转过3°，计0.000 344 827 s为一个时间步，每时间步内的最大迭代次数设为30，共计算了6圈，计0.248 276 s。

压力脉动的原因非常复杂，结构原因、动静干涉、二次流、汽蚀均可引起。小流量时，流道中出现的涡流通常为湍流，可以看成是由各种不同尺度的涡叠合而成的流动。大尺度的涡，主要由流动的结构边界条件决定，其尺寸可以与流场的大小相当，主要受惯性影响，是引起低频脉动的原因。小尺度的涡主要由粘性力所决定，其尺寸可能只有流场长尺度的千分之一，是引起高频脉动的原因。根据奈奎斯特采样定理，采样频率应大于或等于有效信号最高频率的两倍，采样值就可以包含原始信号的所有信息。本文的关注点是双层流道结构对外特性宏观量的影响。按转速1 450 r/min的叶轮每圈120个采样点计，采样频率达2 900 Hz，可满足对大尺度压力脉动影响因素的分析。

用以上同样的非定常计算设置，对普通泵和λ=1/3的双层流道泵作了数值计算，P1～P15点的压力时间序列如图12所示，以每条取样线上的5个点为一组。各监测点数值均为上下波动，因P4、P5点位于双层流道内部，P8、P9位于内筒出口后，这4点在加装内筒后振幅明显增加。P11、P12点位于转角区，易发生流动分离，有或无内筒时在现采样频率下波形均呈现突变特性。

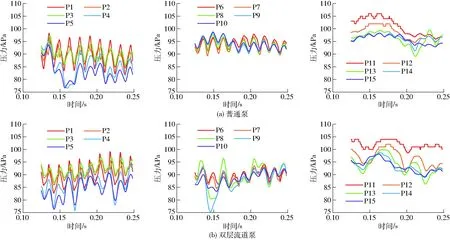
图12 压力监测点的时间序列图Fig.12 Time series diagrams of pressure at monitoring points

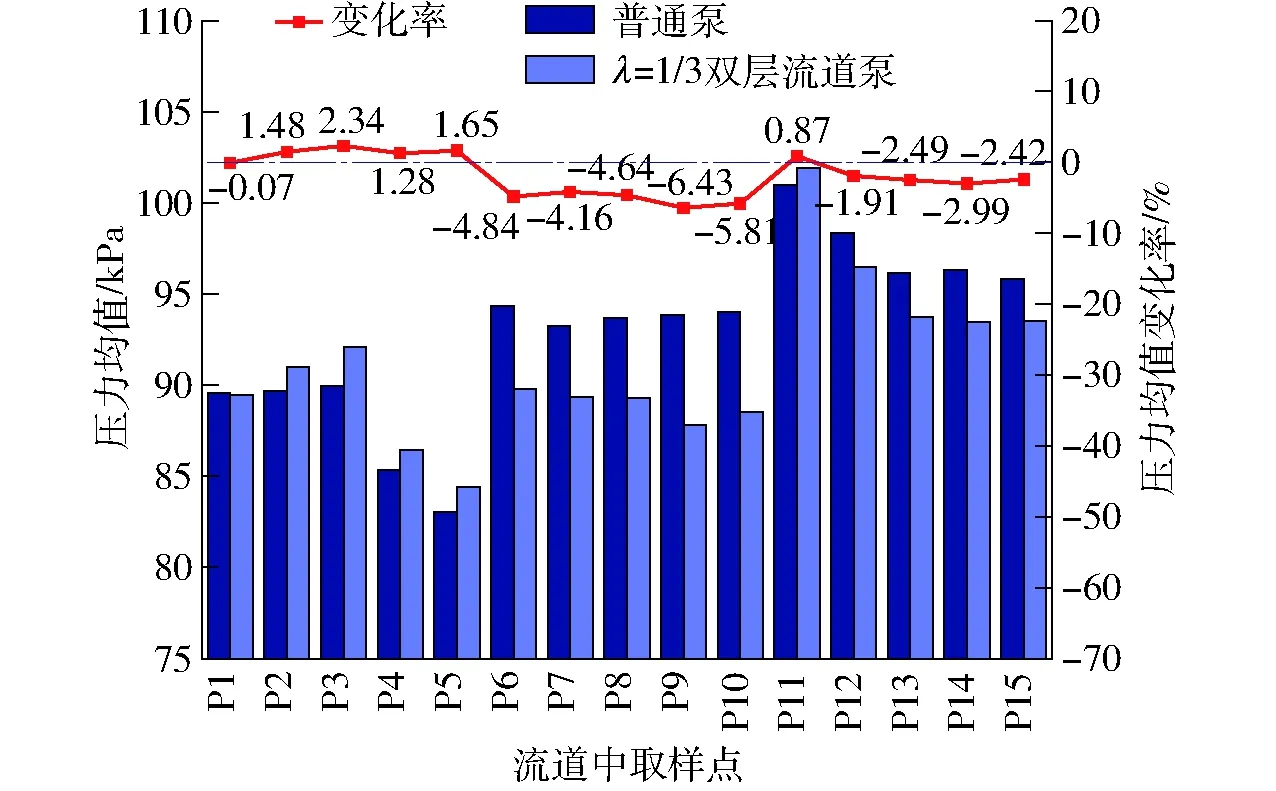
图13 监测点的压力均值变化Fig.13 Pressure mean value comparison between normal pump and λ=1/3 structured pump

图13为压力快速傅里叶变换(FFT)后每采样点压力的0频分量，对压力脉动此分量等于采样区间压力均值。红线为加装双层流道后压力均值变化率，明显可见大部分监测点压力下降，最大值为-6.43%，意味监测点处流速的上升。P11～P15一组的位置处于流动下游，压力明显高于P6～P10组。P6～P10组也同样高于P1～P5组。

压力值振幅的频域图如图14所示。频域分析中以轴频作为基频fn，图像的横坐标为FFT各频率分量与基频的比值f/fn。因叶轮有3个叶片，可见3倍频处幅值出现了递减的波峰。但所有监测点在3fn后的振幅值都大幅减弱。

双层流道结构明显降低了P4、P5点在低频时的幅值，说明双层流道对叶轮出口边后的区域有抑制脉动作用。叶频3fn为最大振幅频率点，双层流道也降低了此频率点的振幅。P8、P9点在有双层流道时轴频处的振幅增加，与其位置靠近双层流道出口有关。P11点在轴频处的一个脉冲在加装双层流道后得到大幅抑制。

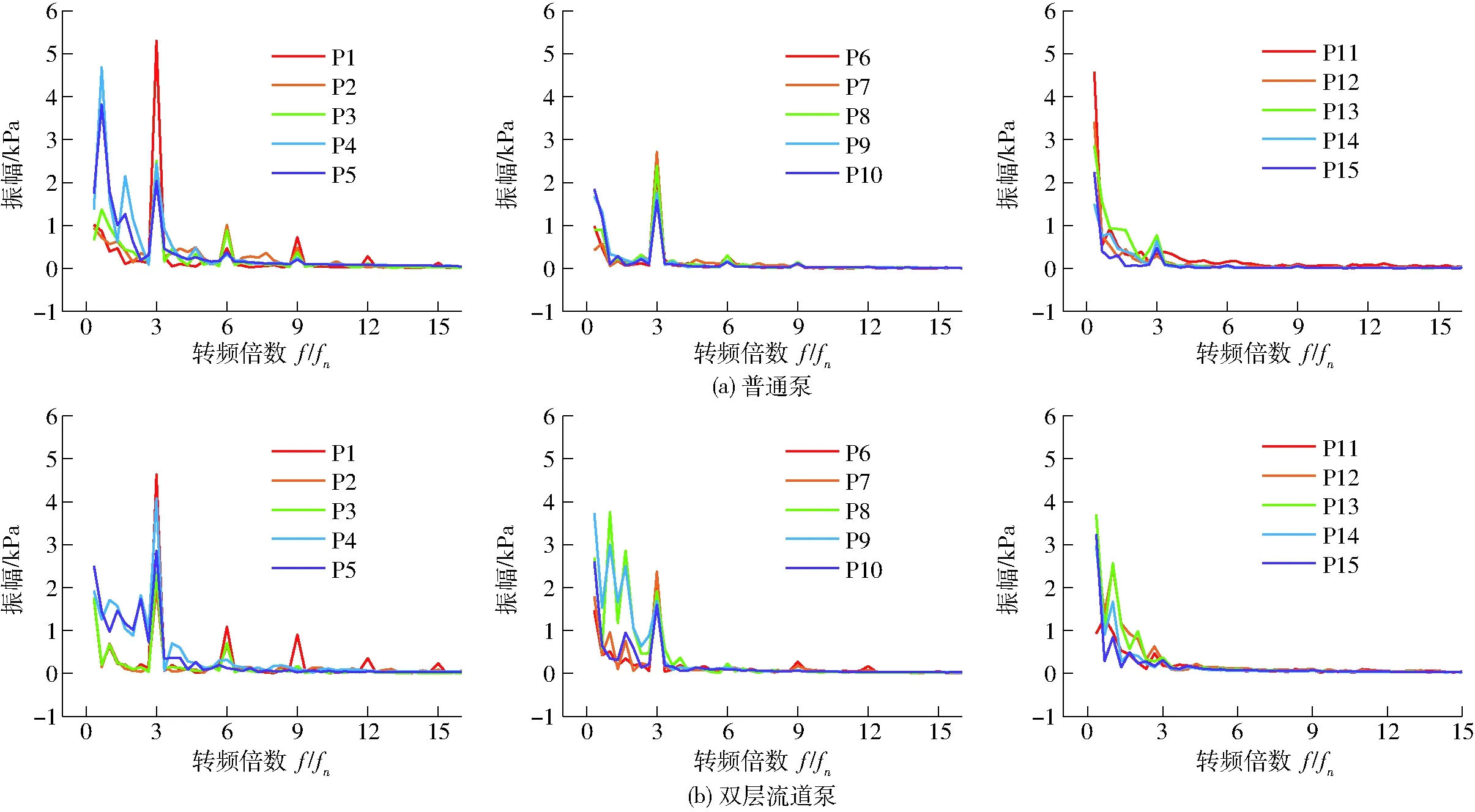
图14 快速傅里叶变换后压力监测点的频域图Fig.14 Frequency domain diagrams of pressure after FFT

4.3 不同λ值对外特性的影响

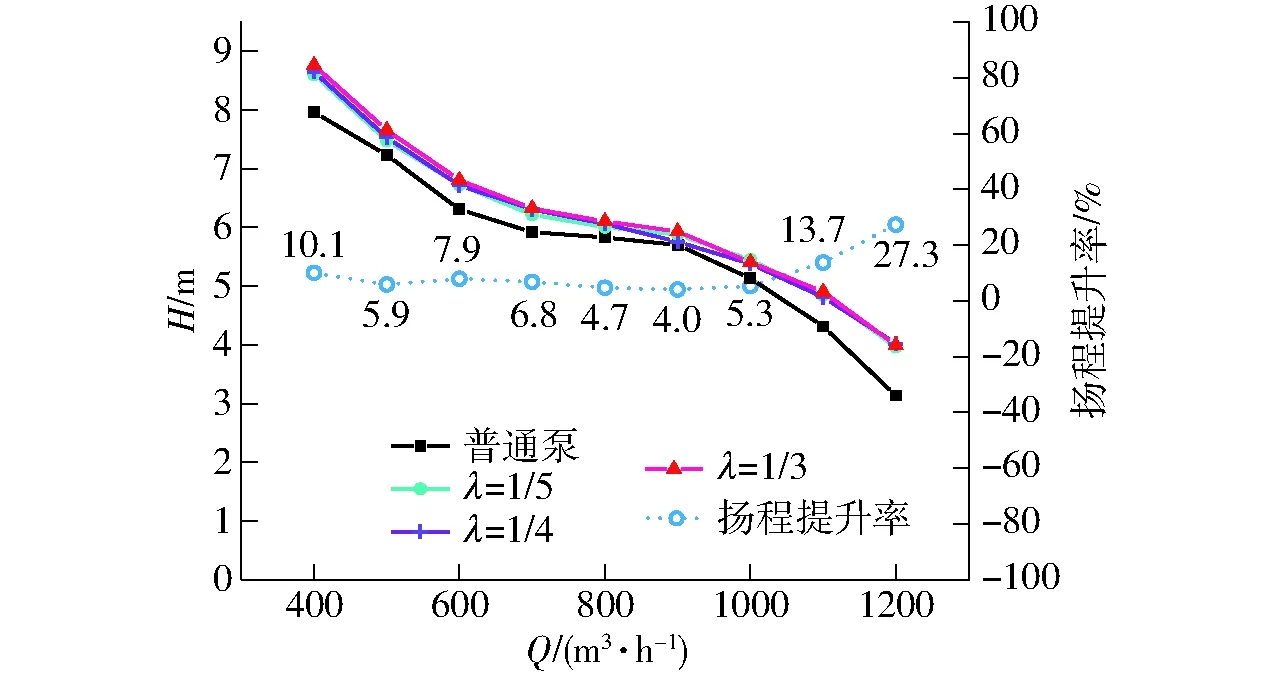
图15 普通泵与双层流道泵的流量-扬程曲线Fig.15 Flow-head curves of normal pump and double layer structured pumps

普通泵与不同间距值双层流道泵的流量-扬程曲线计算结果如图15所示。3种双层流道泵的曲线整体位置均在普通泵之上。在1 000 m3/h以上的大流量工况下，不同λ的双层流道泵比无内筒普通泵扬程均有明显上升。在小流量工况下，扬程也均有所增加。

相比于无内筒普通泵，在0.8Qd～Qd不稳定范围内，双层流道泵的扬程位于高处，不再出现流量减少时扬程不上升的情况，曲线的马鞍形消失，不再有拐点。因此，双层流道设计有效改善了此模型流量-扬程曲线的马鞍形区间，提高了全流量范围的扬程。对比3种间距的结果可发现，当λ=1/3时，扬程上升的幅度最大。

图15中蓝色虚线表示λ=1/3双层流道泵对比普通泵的扬程提升率，在大流量工况时效果更优。对λ=1/3与λ=1/4和λ=1/3与λ=1/5结构方案的结果分别作了对比，扬程的最大差别为3.06%和3.58%，均低于4%。出于工程化考虑，可优先考虑λ=1/3的结构。

在小流量工况下，双层流道泵与普通泵的效率基本一致；在大流量1 000 m3/h以上的工况下，双层流道泵的效率也有所增加。原因是双层流道结构减少了导叶出口下游的边界层流动分离，其正面效应大于加装内筒对液流的阻碍作用。流量-效率曲线如图16所示。

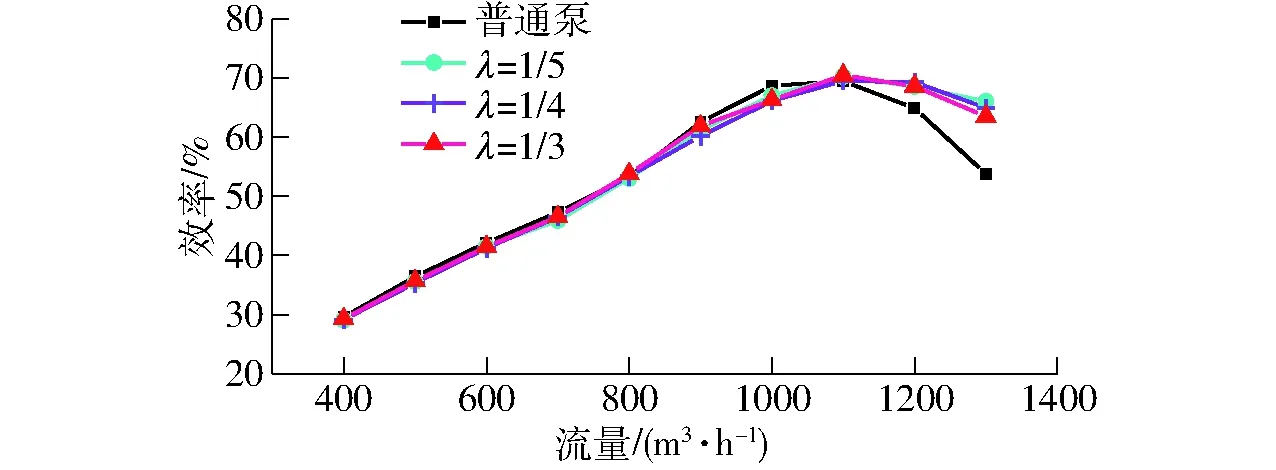
图16 普通泵与双层流道结构泵的轴流泵效率曲线Fig.16 Flow-efficiency curves of normal pump and double layer structured pumps

5 结论

(1)全工况下电机内置式潜水轴流泵的流量-扬程曲线随着流量减小出现了马鞍形区域。在小流量工况下，因不同半径处的扬程出现差异，叶片出口后的流场受到破坏，流动偏向流道外侧。随着流量的减小，叶片出口后的漩涡区域逐渐增加，占据主流的比例也逐渐扩大，从而影响了轴流泵机组的扬程、效率及稳定性。

(2)叶轮出口后的双层流道结构在小流量工况时可以有效抑制叶片出口后回流的发生，减轻涡旋数量与强度，从而改善了叶片出口后的的流场，提高了小流量下的扬程。

(3)在设计工况和大流量工况时，双层流道结构在导叶流道内起到导流作用，减少了后续流动的层间影响，双层流道间隙内的流动方向与主流一致，对导叶后扩散出水管内的边界层流动分离有明显抑制作用，减小了涡旋影响区域，扩大了主流通道，明显提升了扬程与效率。

(4)双层流道的λ取1/3时扬程提升效果最佳，3种间距的扬程差别在4%以内。