“数”之严谨“形”之直观
文/康叶红
方程是研究已知量和未知量关系的模型。求方程的解,就是利用等式的基本性质和代数式的运算,将方程化成最简形式“x=a”。此外,我们还可以从“形”的角度来求方程的解,下面从图形解法和函数图像解法两个方面来谈谈方程的解法。
一、图形解法与方程
苏科版数学教材九年级上册第12页“数学实验室”中有这样一个问题:
例1用配方法解一元二次方程x2+2x-24=0,配方法的过程可以用拼图直观地表示。
【分析】求一元二次方程的解常用的方法有直接开平方法、配方法、公式法、因式分解法。此外,我们还可以用拼图的方法(如图1)直观地描述配方法的过程,在操作中感受数与形的结合。
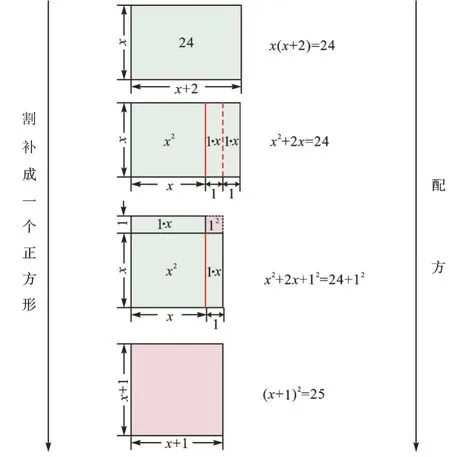
图1
变式请用图形求解一元二次方程x2+2x-24=0的正根。
【分析】求解一元二次方程x2+2x-24=0的正根的过程,可以这样来思考:①变形,得x(x+2)=24;②画4个长为x+2,宽为x的矩形,构造一个边长为(x+x+2)2的正方形(如图2);③图2中的大正方形面积可以表示为(x+x+2)2,或4个长为(x+2)、宽为x的矩形的面积之和,加上中间边长为2的小正方形面积,即4x(x+2)+22。
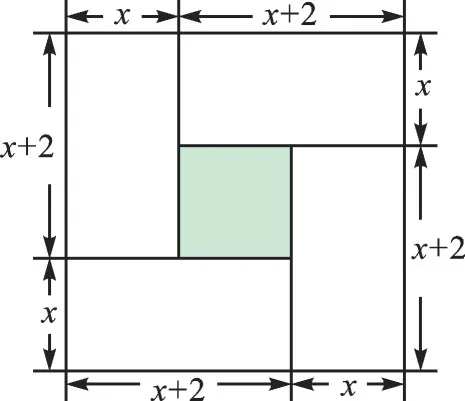
图2
解:(x+x+2)2=4x(x+2)+22,
因为x(x+2)=24,
所以(x+x+2)2=4×24+22,(2x+2)2=100,
因为x>0,所以x=4。
【总结】利用图形直观表示配方法求解过程,充分体现了数形结合的思想方法。借助于形的直观和数的严谨两方面求解问题,拓宽了解题思路。
我们还可以将这个过程一般化,求关于x的一元二次方程x(x+b)=c(b>0,c>0)的正根的过程,就是利用4个长为x+b、宽为x的矩形,构造边长是x+x+b的正方形(如图3),则图中的大正方形面积可以表示为(x+x+b)2,或4个长(x+b)、宽x的矩形的面积之和,加上中间边长为b的小正方形面积,即4x(x+b)+b2。由此可得方程的正根是
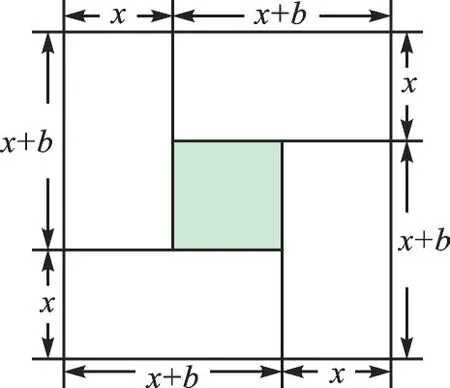
图3
二、图像解法与方程
苏科版数学教材八年级上册第161页向大家介绍了利用一次函数的图像可以求二元一次方程组的解,具体如下:
例2利用一次函数的图像解二元一次方程组
【分析】我们可以借助代入消元法或者加减消元法来求二元一次方程组的解,得我们还可以用一次函数的图像来求二元一次方程组的解,即一次函数和y=2x-3的图像交点坐标是(2,1),那么二元一次方程组的解是
变式解方程x3-2x2-9x+18=0。
解法1:x2(x-2)-9(x-2)=0,
(x-2)(x2-9)=0,
(x-2)(x+3)(x-3)=0,
所以x1=2,x2=-3,x3=3。
【总结】类比之前已学过的各类方程的解法,应把一元三次方程通过降次转化为一次方程来进行求解。
解法2:由x3-2x2-9x+18=0,
得x3=2x2+9x-18。
在同一个平面直角坐标系中,画出函数y=x3和函数y=2x2+9x-18的图像(如图4),它们 的 交 点 坐 标 为A(2,8),B(-3,-27),C(3,27),所以x1=2,x2=-3,x3=3。

图4
【总结】利用两个函数的图像可以求解方程,将方程的解转化为两个函数图像的交点坐标,这里可以看成函数y=x3和y=2x2+9x-18的图像的交点坐标。
数形结合思想是研究数学问题的有效方法之一,利用数量与图形、数量与图像之间的关系,“以形助数”,使复杂问题简单化,抽象问题具体化,强化代数推理意识,无疑也是求解问题的良策。

