把脉方程与不等式问题中的易错点
文/张田田

方程与不等式是刻画现实世界数量关系的有效模型,反映的是数学中“相等”与“不等”两种基本的数量关系,是解决数学问题和生活实际问题的有力工具,是中考考查的重要内容。在做题的过程中,不少同学觉得,有的题明明会做,可还是错了;有的题看着挺眼熟,可就是不知如何下手……接下来,本文从中考中寻找易错的题型,抓住考查的要点,揭秘方程与不等式易错题背后的错因。
例1解方程:x(x-7)=8(7-x)。
【典型错误】方程两边同时除以(x-7),得x=-8。
【错因分析】运用等式的基本性质,等式两边同除以一个不为零的数或式子,但除以(x-7)时未考虑x-7=0的情况,所以方程“失”去了一个根。
【正解】x(x-7)-8(7-x)=0,
(x-7)(x+8)=0,
x-7=0或x+8=0,
所以x1=7,x2=-8。
【点评】解一元二次方程时,若方程有实数根,一定有两个(相等或不相等)实数根。如遇到x(x-7)=8(7-x)这种形式的方程时,不能两边同除以(x-7),而应先移项、再提公因式,一边因式分解为两个一次因式的乘积,另一边是0,谨防失根的情况出现。
例2解方程
【典型错误1】方程两边同时乘(x+1)·(x-1),得2(x-1)+1=x(x+1)。
方程无解。
【典型错误2】方程两边同时乘(x+1)(x-1),得2(x-1)+(x+1)(x-1)=x·(x+1)。
解得x=3。
【错因分析】根据等式的基本性质,方程两边同时乘最简公分母(x+1)(x-1),应乘方程的每一项,而“典型错误1”中的常数项1没有乘(x+1)(x-1),与原方程不是同解方程。“典型错误2”是没有将求出来的根进行检验,不确定其是否为增根,这样解出的根可能导致分母为0。
【正解】方程两边同时乘(x+1)·(x-1),
得2(x-1)+(x+1)(x-1)=x(x+1)。
解得x=3。
检验:当x=3时,(x+1)(x-1)≠0。
所以,原方程的解为x=3。
【点评】由于解分式方程需要去分母,转化为整式方程求解,所以可能会产生增根,因此需要进行检验。同时,应用等式基本性质时,不要漏乘。碰到类似题目时,一是不要图快而遗漏,二是一定要记得检验。
例3以下是圆圆解不等式组的解答过程:
解:由①,得2+x>-1,所以x>-3。
由②,得1-x>2,所以-x>1,
所以x>-1。
所以原不等式组的解是x>-1。
圆圆的解答过程是否有错误?如果有错误,请写出正确的解答过程。
【错因分析】在去括号的过程中,需要与括号里的每一项相乘,所以解不等式①不对;不等式两边同时除以-1时,不等号的方向要改变,所以解不等式②不对。
【正解】圆圆的解答过程有错误。
正确过程如下:由①,得2+2x>-1,
∴2x>-3,
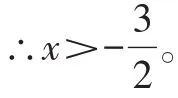
由②,得1-x<2,
∴-x<1,∴x>-1。
∴不等式组的解集为x>-1。
【点评】解不等式时,两边同乘负数,不等号的方向要改变;不等式组的解集可以借助“同大取大,同小取小,大小小大中间找,大大小小无处找”,也可以画数轴求解。
例4已知关于x的一元二次方程x2-mnx+m+n=0,其中m、n在数轴上的对应点如图所示,则这个方程的根的情况是( )。

A.有两个不相等的实数根
B.有两个相等的实数根
C.没有实数根
D.无法确定
【典型错误】C或D。
【错因分析】虽然根据数轴可以判断m、n的符号,但是不一定联想到m+n、mn的符号,从而不能判断根的判别式。也有同学直接去求方程的根,但随后却无从下手。
【正解】由数轴,得m>0,n<0,m+n<0,
∴mn<0,
∴b2-4ac=(-mn)2-4(m+n)>0,
∴方程有两个不相等的实数根。故选A。
【点评】判断一元二次方程根的情况,我们首先想到根的判别式,然后根据题目所给条件进行判断。

