实数的六个命题点

文／刘琼琼

实数是中考重点考查的知识点之一，但许多同学认为实数内容相对简单，不太重视实数的学习，从而在解决与实数相关的题目时出现会做但做错的现象。现从六个命题点进行知识梳理，查漏补缺，以期对同学们的复习有所帮助。

命题点一：绝对值、相反数、倒数

例1（1）-2021的绝对值是（ ）。

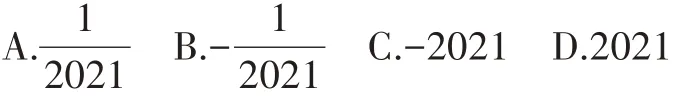
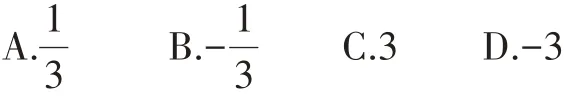
（3）实数100的倒数是（ ）。

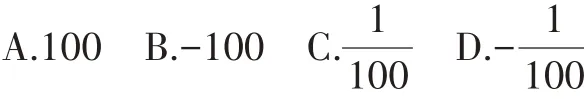
【解析】根据绝对值、相反数、倒数的概念解题。（1）D；（2）A；（3）C。

【点评】（1）正数的绝对值是它本身，负数的绝对值是它的相反数，0的绝对值是0。（2）一个正数的相反数是负数，一个负数的相反数是正数，0的相反数是0。（3）求一个数的倒数有以下技巧：①求整数的倒数，可以把整数看成是分母为1的分数，再把分数的分子、分母颠倒位置即可；②求真分数的倒数，直接把分数的分子、分母颠倒位置即可；③求一个小数的倒数，先把小数化成分数，再求其倒数；④求一个带分数的倒数，先把带分数化成假分数，再求其倒数。

命题点二：科学记数法

例2（1）2021年扬州世界园艺博览会以“绿色城市，健康生活”为主题。在某搜索引擎中输入“扬州世界园艺博览会”，约有3020000个相关结果，数据3020000用科学记数法表示为_____。

（2）原子很小，1个氧原子的直径大约为0.000000000148m，将0.000000000148用科学记数法表示为_____。

（3）据国家卫生健康委员会发布，截至2021年5月23日，31个省（区、市）及新疆生产建设兵团累计报告接种新冠病毒疫苗51085.8万剂次，将“51085.8万”用科学记数法表示为（ ）。

A.0.510858×109B.51.0858×107

C.5.10858×104D.5.10858×108

【解析】科学记数法是把一个数写成a×10n的形式，1≤ ||a＜10，n为不等于0的整数。（1）3.02×106；（2）1.48×10-10；（3）D。

【点评】把一个数用科学记数法表示的方法：（1）a值的确定，1≤ ||a＜10。（2）n值的确定，当原数的绝对值≥10时，n是正整数，n的值等于原数的整数位数减1或原数变为a时小数点向左移动的位数；当0＜原数的绝对值＜1时，n是负整数，n的绝对值等于原数中左起第1个非零实数前零的个数（包括小数点前面的0）或原数变为a时小数点向右移动的位数。另外还要注意原数字后面的万、亿等单位，以及结果是否需要计算。

命题点三：数轴的应用

例3实数a、b在数轴上的对应点的位置如图所示，下列结论中正确的是（ ）。

A.a＞-2 B.||a＞b

C.a+b＞0 D.b-a＜0

【解析】观察数轴得出a＜-2，b＞0，||a＞|b|，故A选项错误，B选项正确；根据有理数的加法法则a+b＜0，C选项错误；因为b＞a，所以b-a＞0，D选项错误。故选B。

【点评】观察数轴上的数应从三个方面入手：（1）数的正负性；（2）绝对值大小；（3）利用数轴比较大小（数轴上右边的数总大于左边的数）。解决此题需要把数与形结合起来，体现了数形结合思想。

命题点四：平方根、算术平方根、立方根

例4（1）49的平方根是_____ 。

（2）4的算术平方根为_____。

（3）64的立方根是_____。

【解析】根据平方根、算术平方根、立方根的概念解题。（1）±7；（2）2；（3）4。

【点评】非负数a的平方根是±，算术平方根是，实数b的立方根是。

命题点五：无理数的估算

例5 若m＜2＜m+1，且m为整数，则m=____。

【解析】因为，所以5＜＜6，所以m=5。

【点评】估算的取值范围，需从两个方面入手：（1）确定与a相邻的两个完全平方数，即比a大和比a小且最接近a的两个完全平方数；（2）分别求出这些完全平方数的算术平方根，从而得出m的值。

命题点六：实数的运算

例6

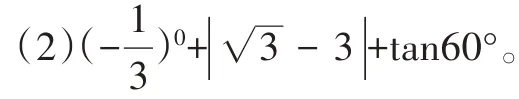
【解析】（1）和（2）涉及绝对值、零指数幂、立方根、负指数幂、特殊角的三角函数值等考点。在计算时，我们首先应针对每个考点分别进行计算，然后根据实数的运算法则求得计算结果。

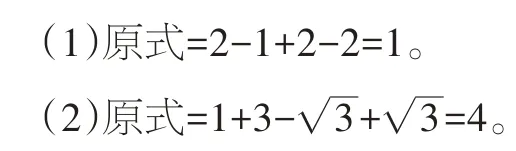
【点评】实数的运算通常将绝对值、算术平方根、立方根、零指数幂、负指数幂、特殊角的三角函数等考点集于一题，综合考查运算能力。解题时要注意以下几点：（1）零次幂，a0=1（a≠0）；（2）负整数指数幂，p为正整数），特别地；（3）熟记特殊角的三角函数值；（4）注意各项的符号。