大型浮体浮筒纵横置方案的载荷和结构响应研究
罗文平 刘维勤 屈毫拓 宋学敏
(武汉理工大学船海与能源动力工程学院1) 武汉 430063) (教育部高性能船舶技术重点实验室2) 武汉 430063)
0 引 言
大型浮体(very large floating structures, VLFS)机动灵活、造价较低、对环境影响小[1],其载荷和结构响应评估是平台设计的重要内容.Suzuki[2]运用多种方法,对日本VLFS的安全性进行了研究.栾道坤[3]研究了VLFS的结构设计、连接器方式、频域时域分析、强度计算和疲劳寿命分析.张海成等[4-6]基于最新引入的网络动力学理论,研究了VLFS中的各式连接器、多模块连接和刚柔耦合的非线性动力响应特征及预报,但该理论还没有经过试验验证.VLFS同属于半潜式海洋平台,在波浪载荷的计算中,通常采用设计波法.李红涛[7]将确定性设计波法、随机性设计波法和长期预报设计波法应用于半潜式平台波浪载荷计算,并进行了对比分析,建议初步设计时使用确定性设计波法.严文君等[8]研究了多种工况下半潜平台的响应及强度分析,发现规范推荐的设计波短期预报法过于保守,并且规范推荐的设计波工况不一定是结构最危险的情况,需要结合半潜平台实际特点综合确定;研究表明确定性设计波法适用于结构的初步设计,但设计波参数需要自行综合确定.基于三维势流理论进行研究,已广泛应用于VLFS.阚涛等[9]基于三维势流理论对FLNG进行水动力分析,并根据设计波法完成强度计算.杨树耕等[10]基于三维势流理论,应用Sesam计算了大尺度构件的水动力响应,预报了算例平台三个自由度的动力特性.可以看出使用三维势流理论计算波浪载荷已经成熟,且结果可靠.
半潜式平台采用小水线面的浮筒-立柱结构,具有小波浪力和小运动的特点,成为VLFS结构的主要船型.但VLFS结构因细长特点,目前采用的半潜型式有浮筒横置式和浮筒纵置式两种[11-13],相同排水量下的浮筒横置式平台和浮筒纵置式平台的载荷及响应特性有待研究,用以指导某VLFS结构的总体设计[14-15].文中采用三维势流理论的波浪载荷求解器Hydrostar计算VLFS的波浪载荷,根据载荷计算结果确定设计波法的波浪海况参数,基于流固耦合平台Homer联合调用水动力求解器Hydrostar和结构有限元求解器Nastran,对海上浮式平台结构进行设计波下的结构响应分析.
1 基于三维势流理论的边界元法
求解VLFS结构流体动力时,基于三维势流理论,假设流体无旋、无粘、不可压缩,边界元法在此基础上结合了格林函数与湿表面物面条件.流场总的速度势包括入射势、绕射势和辐射势.
Φ(xi,yi,zi)=ΦI(xi,yi,zi)+ΦS(xi,yi,zi)
(1)
式中:Φ为总速度势;ΦI为入射势;ΦS为待求物面势,包含绕射势和辐射势.入射波取单一频率、单一方向的平面波,作为已知给出,入射波速度势定义为
(2)
式中:H为波高;w为频率;d为水深.求解波浪载荷就必须求解速度势,入射势已经给出,只需求解物面势,将物面势写为
ΦS(xi,yi,zi)=φSe-iwt
(3)

于是得到如下积分方程.
=2un(x,y,z)
(4)
式中:un(x,y,z)为入射波引起物面法向流体速度.对该积分方程进行数值求解,假定湿表面模型有限个面元上的源强是常数,在每个面元中点计算格林函数及其导数,积分方程则化为离散形式,表示成矩阵进行求解,得到速度势,最后积分得到波浪载荷,这就是基于三维势流理论的边界元法求解过程.
2 计算模型
2.1 模型概述
某VLFS采用半潜式结构,由上层平台、立柱及底部浮筒组成,每个平台有八根立柱,四个浮筒.上层平台是长110 m、宽40 m、高6 m的矩形体结构;立柱是长、宽均为7 m、高15 m的柱体结构,沿船长方向等间距分布;底部浮筒是长40 m、宽14 m、高9 m的椭圆柱结构.为研究浮筒布置对平台载荷和结构响应的影响,选用VLFS的浮筒横置与浮筒纵置两种设计方案,见图1,两型平台的设计重量相同,设计吃水相同,浮筒排水量相同,针对这两种浮筒横置与浮筒纵置平台模型,分别建立其水动力模型和结构有限元模型,进行载荷和结构响应分析.

图1 两型平台效果图
2.2 水动力模型
两型平台的水动力模型只需建立水线以下部分的外表面面元网格,用于计算波浪载荷.除浮筒布置形式差异外,浮筒与立柱的形状、尺寸均相同,见图2.横置平台水动力模型网格单元数5 537,纵置平台水动力模型网格单元数5 728,网格数量基本相同.

图2 两型平台水动力网格模型
2.3 结构模型
建立两型平台的结构有限元模型用于评估两型平台结构响应.横置与纵置平台结构除浮筒布置方向的差异之外,其他均相同,设计排水量均为20 459 t,两型平台在各个位置的板材与型材均取相同型号,并对两型平台进行相同的网格划分.横置平台结构总重11 386.06 t,纵置平台结构总重11 369.81 t,重量基本相同.横置平台网格单元数为48 448,纵置平台网格单元数为47 208,网格数量基本相同.长度方向定为x轴,宽度方向定为y轴,垂直方向定为z轴.使用Patran进行有限元模型的建模,结构模型见图3.
图3 两型平台结构网格模型
2.4 静水弯矩
静水弯矩可以反映结构本身布置导致的静水受力情况,由浮力和重量分析共同决定.水动力模型提供浮力分布,结构模型提供重力分布,得到两型平台的静水弯矩曲线,见图4.由图4可知,在静水工况下,横置平台的最大弯矩略小于纵置平台的最大弯矩.由于两型平台的浮筒提供的浮力在纵向不连续且位置存在差异,而重力连续,导致横置平台的静水弯矩在纵向出现四个峰值,分布非常集中;纵置平台的静水弯矩出现两个峰值,分布较为均匀.
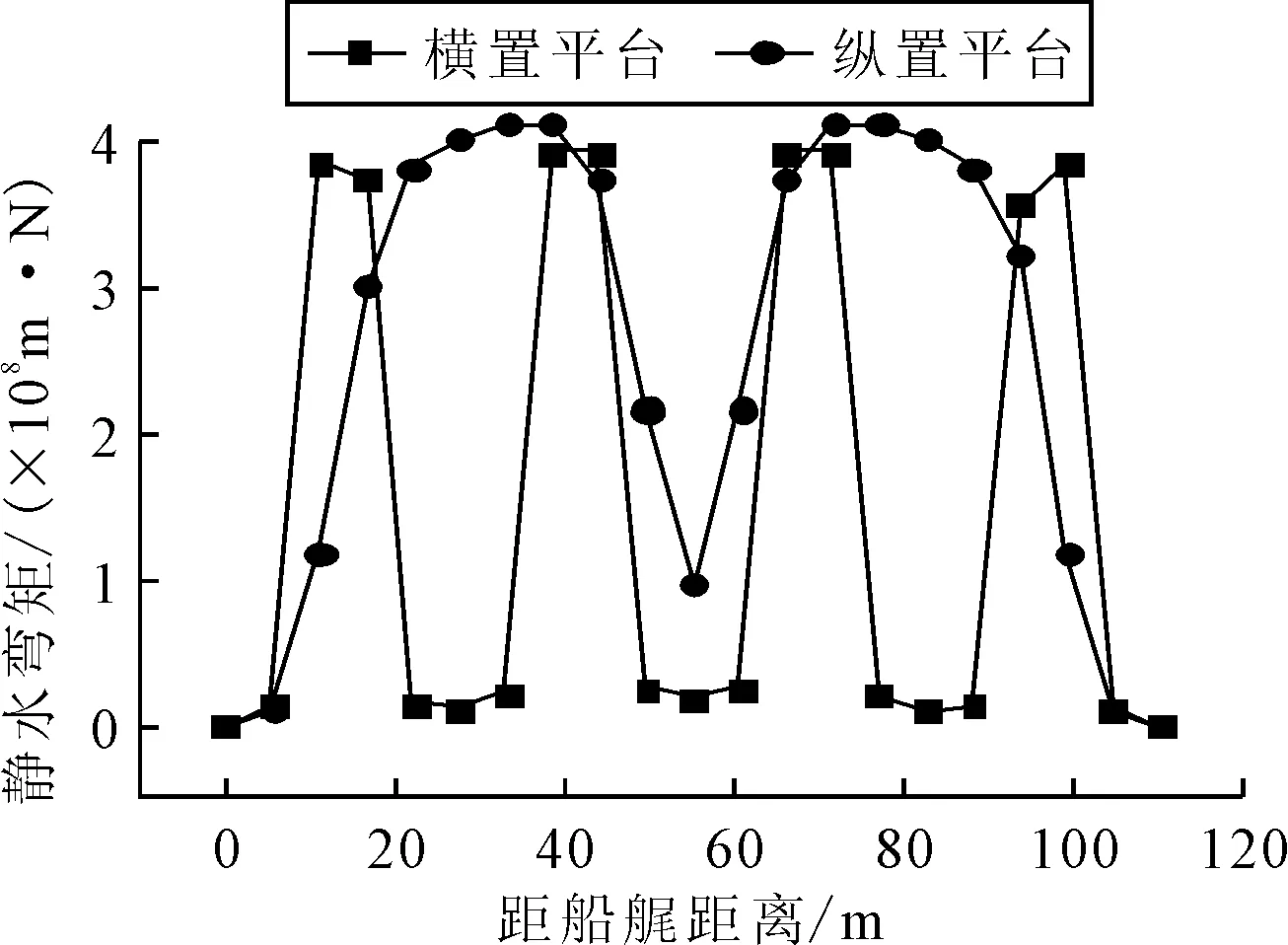
图4 两型平台静水弯矩
3 两型平台的波浪载荷
采用基于三维势流理论的Hydrostar软件计算两型平台的波浪载荷.根据《钢质海船入级规范》选择输入工况,浪向角从船首开始取0°~180°,每隔30°取一个浪向,共七个浪向角;波浪角频率范围从0.4取到1.8 rad/s,每隔0.02 rad/s取一个角频率.将水动力模型导入,计算得到不同剖面位置的横向弯矩与纵向弯矩的RAO数值.
由于剖面数量过多,平台属于对称结构,因此选取典型船中横剖面处0°~90°的纵向弯矩MY(见图5)与船中纵剖面处0°~90°的横向弯矩MX(见图6)的RAO数值进行汇总和比较.
1)比较图5~图6的数值大小,发现两型平台在0°浪向MY作用下时都产生最大响应,角频率在0.7~0.8 rad/s.
2)两型平台RAO(MX)明显小于RAO(MY)的数值.在图6d)90°横浪下RAO(MX)达到最大峰值,接近8×107,而在图5a)0°迎浪下RAO(MY)达到最大峰值,接近13×107.除此外,其他浪向下的数值差异更加显著.
3)由图5可知,横置平台的纵向弯矩MY明显大于纵置平台,横置平台的MY峰值近乎为纵置平台的2倍,应引起设计者的重视;由图6可知:除60°浪向外两型平台的横向弯矩MX差别不大.

图5 两型平台各浪向角下RAO(MY)
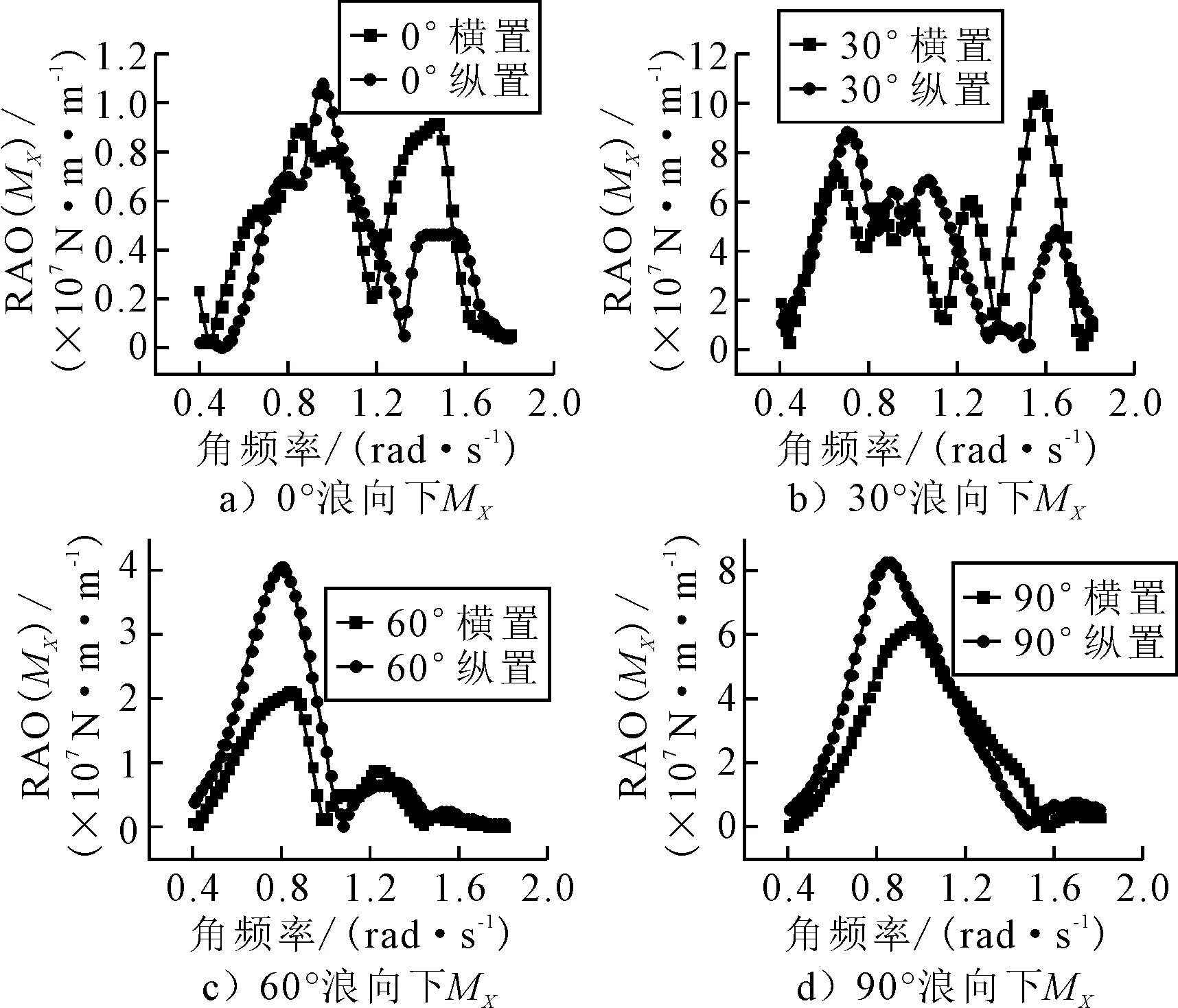
图6 两型平台各浪向角下RAO(MX)
4 结构安全性分析
4.1 边界条件
由于模型处于平衡状态,结构分析时仅需设置约束其六个自由度刚体位移的边界条件即可.对模型施加边界条件,设置尾部左侧纵向和垂向线位移,即TX=TZ=0,设置尾部右侧横向和垂向线位移,即TY=TZ=0,设置首部中间横向和垂向线位移,即TY=TZ=0.
4.2 设计波参数的确定
将波浪载荷计算分析得到的能使两型平台产生最大响应的波浪因素作为确定设计波的参数:频率0.74 rad/s、浪向角0°;结合南海近岛礁海域波浪的实际情况,选取百年一遇的8.19 m作为设计波波高,将该设计波下的工况作为波浪工况,见表1.

表1 设计波参数
4.3 计算结果
使用Homer进行静水工况和波浪工况下的强度直接计算,图7为静水工况下两型平台的von Mises应力云图.两型平台均为对称结构,纵向长度较长,在船中处受力明显且变化较大,因此选取位于甲板中心处的一块板单元作为分析对象,得到波浪工况下的甲板中心点处的应力时域曲线,见图8.
分析两型平台甲板中心单元应力时域图,由于波浪周期变化引起两型平台发生中垂中拱,作用于甲板中心板单元上的应力也随时间呈现出周期变化.横置平台甲板中心处板单元应力水平显著大于纵置平台,横置平台最大为70 MPa,纵置平台最大为40 MPa;横置平台中垂中拱时应力水平一致,纵置平台有效降低了中垂中拱应力水平,结构安全性更高;两型平台的剪切应力水平相近,且相比于应力而言其数值很小.在应力云图中,由于受力和结构特点等,两型平台应力均集中于立柱与上层平台连接处、浮筒侧壁和立柱与浮筒连接处,需要特别注意.分析结果可知,纵置平台的应力水平更低,与载荷结果保持一致.
5 结 论
1)横置平台与纵置平台的最大静水弯矩相近,纵置平台的分布更加均匀.
2)两型平台的MY比MX明显更大.各工况的MY除横浪外明显大于MX,平台对于MY更加敏感.
3)横置平台的MY相比于纵置平台更大,两型平台的MX响应差别较小.分别对两型平台的MX与MY进行比较,发现在各浪向下横置平台的MY数值更大,值得设计者注意.纵置平台与横置平台的MX数值相近.
4)通过两型结构强度分析,纵置平台的应力水平明显低于横置平台,与载荷结果保持一致.
文中研究了细长形VLFS结构浮筒横置及纵置类型的载荷及结构强度,但非细长形VLFS结构的浮筒纵横置方案下的载荷和响应还需进一步讨论.

