基于带约束自适应GPC的压水堆蒸汽发生器液位控制研究

叶章林，张雨飞

基于带约束自适应GPC的压水堆蒸汽发生器液位控制研究

叶章林，张雨飞

（东南大学能源与环境学院，江苏 南京 210096）

在压水堆核电站中，蒸汽发生器的液位能否稳定地控制在设定范围内，直接关系到核电站能否安全经济地运行。针对蒸汽发生器液位控制中出现的“虚假液位”、时变以及输入约束等复杂问题，设计了带约束的自适应广义预测控制算法。在此算法中，构建了两输入单输出的数学模型来描述蒸汽流量和给水流量对蒸汽发生器液位的影响，引入了变遗忘因子的最小递推二乘法，对蒸汽发生器的液位对象模型参数进行在线辨识校正；引入逐维重心反向学习的变异策略提高了标准粒子群算法的收敛精度，然后将改进后的粒子群算法用于计算约束范围内给水流量增量的最优值。仿真结果表明，对于蒸汽发生器液位中的复杂控制问题，改进后的广义预测控制器比三冲量PID控制器的控制效果更好。

蒸汽发生器；液位控制；广义预测控制；两输入单输出；在线辨识；粒子群算法

蒸汽发生器是压水堆核电站中一个重要的换热设备，实际运行证明，能否对蒸汽发生器（Steam Generator，SG）液位进行有效的控制直接关系到核电站能否安全经济的运行。当前国内的SG液位控制方法多以PID控制为主[1]，为了优化控制效果，Mayuresh等[2]提出了SG模型预测控制方案，通过辨识出当前的功率水平从而选择合适的预测模型；袁景淇[3]提出的基于状态空间和卡尔曼滤波器的SG预测控制，简化了模型预测控制的计算过程，增强了系统的抗干扰能力，A.G.Parlos等[4]一方面通过构造多步神经预测器用于SG动态建模，一方面采用并行学习结构和梯度下降算法设计了自适应PI控制器。

SG液位控制系统的设计具有以下难点[5]：

（1）SG液位对象是一个动态非线性的非最小相位系统，稳定裕度小，给水流量和蒸汽流量扰动时会出现“虚假液位”现象；

（2）给水流量的变化不能太过剧烈，一般需要限制在10%左右，否则会降低给水阀门的调节能力；

（3）在运行工况发生改变或者受到不确定性干扰时，SG液位对象的参数会随之发生改变，具有时变性。

对此，传统PID控制系统的参数整定复杂，难以在线适应模型的变化，智能算法的控制策略大都只停留在仿真阶段，实际应用具有局限性。1987 年 Clarke[6]等提出的广义预测控制（Generalized Predictive Control，GPC）对模型精确度依赖不高，能有效解决时变和滞后问题，在抑制扰动的同时鲁棒性好，基于这些特点，本文将GPC应用于SG液位控制系统。针对主要的时变、带约束和虚假液位扰动等复杂点，基于粒子群算法设计了自适应带约束的广义预测控制器，并对该控制器进行了仿真验证，结果表明相比常规的三冲量PID控制器，有着更好的控制效果。

1　SG线性化模型及其水位特性

在SG液位控制系统中，大多数研究采用的是Irving[7]所建立的分段线性SG数学模型，该模型的传递函数如式（1）所示。

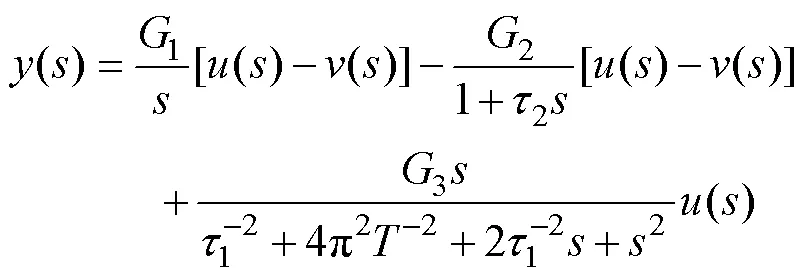
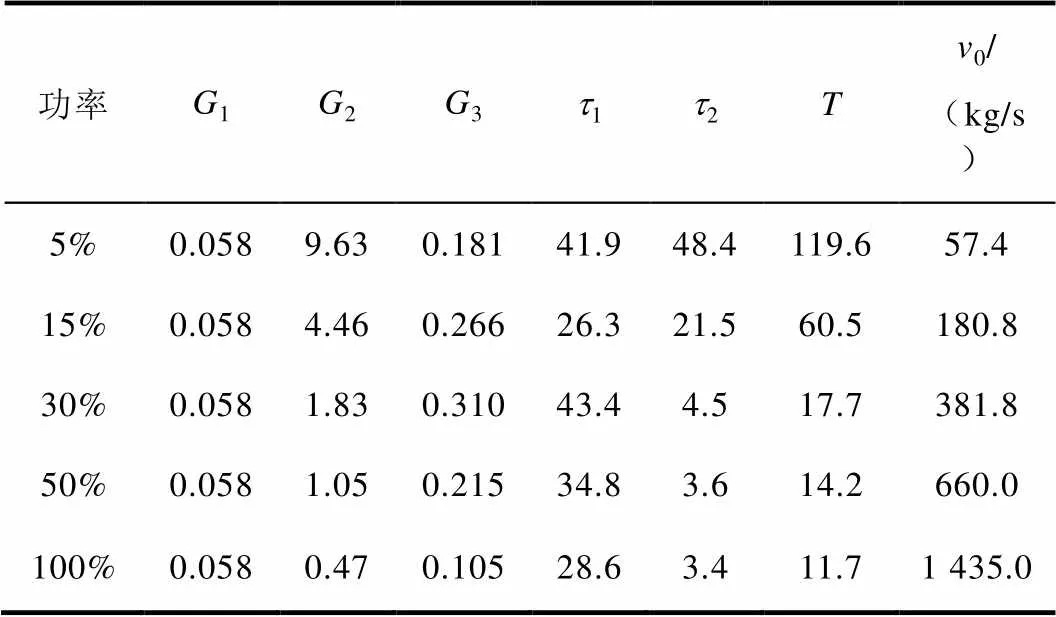
表1　SG线性模型功率点参数表

基于式（1）的数学模型，分别对给水流量和蒸汽流量产生5%的阶跃扰动，在扰动下各个功率点的SG液位动态响应曲线如图 1所示。

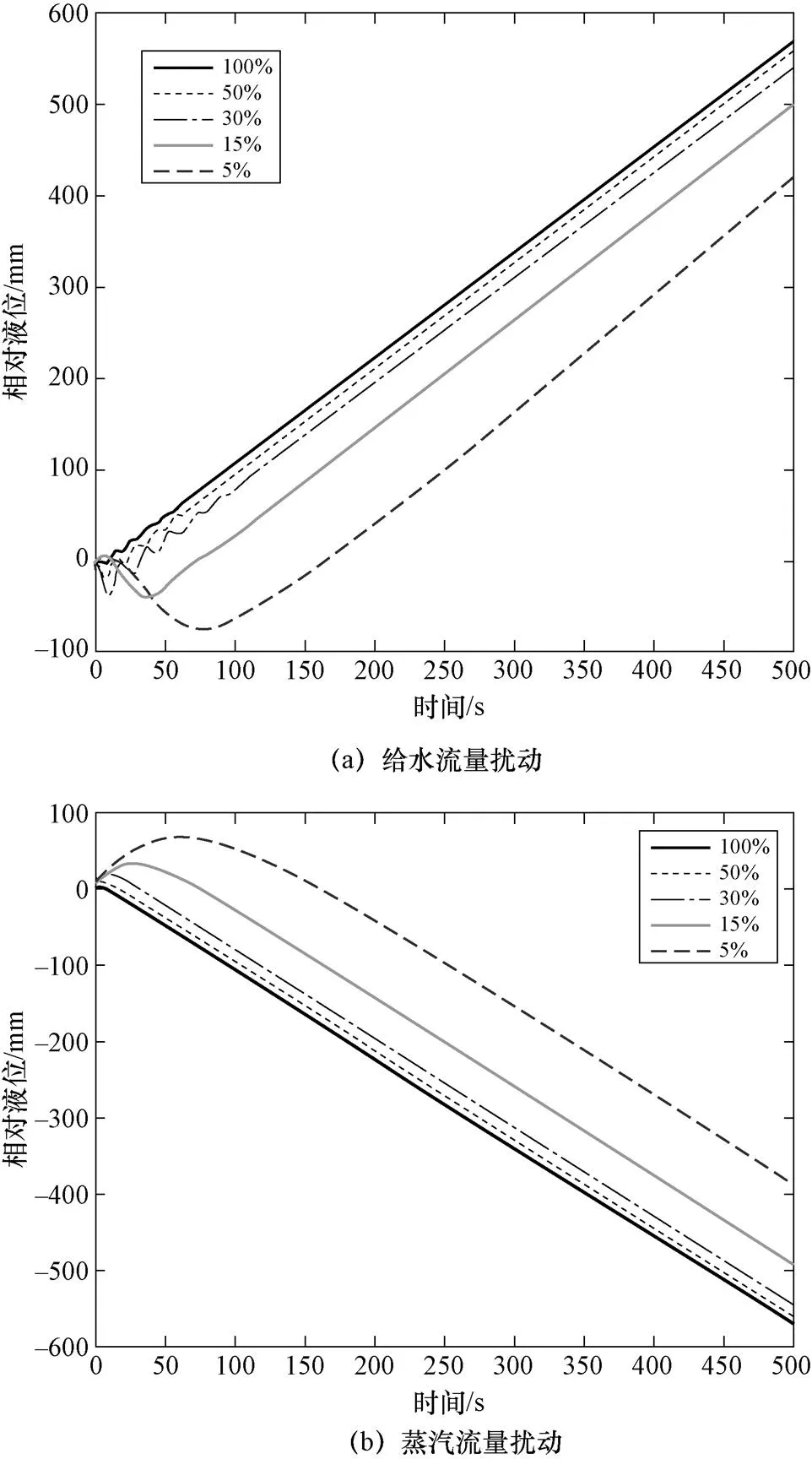
图1　SG液位动态响应曲线

结合图1和文献［8］，对SG液位的特性进行简单的分析：在初期，给水流量和蒸汽流量的阶跃变化，引发了SG中温度和压力的变化，从而引发了含气率的变化，导致循环流量的加速或阻塞，最终形成了反向水位特性，而且随着功率的降低，反向特性更加显著。但随着时间的推移，给水流量或者蒸汽流量始终处于较大的一方，根据质量平衡关系，水位的变化趋势得以恢复正常。

2　粒子群优化算法及其改进

粒子群优化算法（particle swarm optimization，PSO）是由Eberar和Kennedy[9]根据鸟群的捕食行为提出的智能进化算法，其主要思想是将鸟类的捕食过程对应到优化问题的求解过程，每只鸟即为一个可行解粒子，鸟的飞行空间即为问题的解空间，食物的位置为问题的最优解。

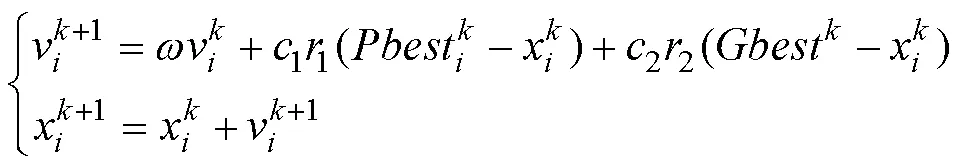
从式（2）可知，粒子速度的更新主要受到上一次的速度信息、自身的飞行经验以及群体的飞行经验的影响，这使得标准PSO的原理简单，参数少，实现容易，能够广泛应用于科学和工程问题。但同时也会导致在算法后期粒子会趋于同一化，种群的多样性降低，从而陷入局部最优解，导致收敛精度不高。

2.1　标准PSO的改进

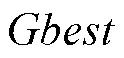
重心反向学习的主要思想是以当前可行解的领域重心作为反向点计算出反向解，进而比较两者的适应度函数值，从中选择更优的作为新的可行解[10]，所涉及到的重心和反向解的定义如下：

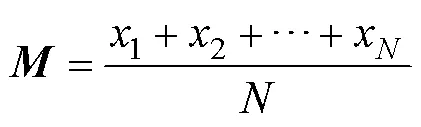
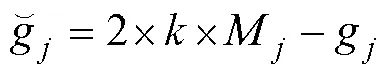
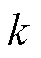
2.2　改进PSO的算法步骤

改进后的PSO算法步骤如下：

（3）根据公式（2）对每个粒子在寻优空间范围内进行速度和位置的更新；

（6）判断是否达到最大迭代次数，若满足则输出结果，若不满足则跳转步骤3。

2.3　改进PSO算法的仿真验证

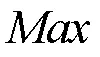
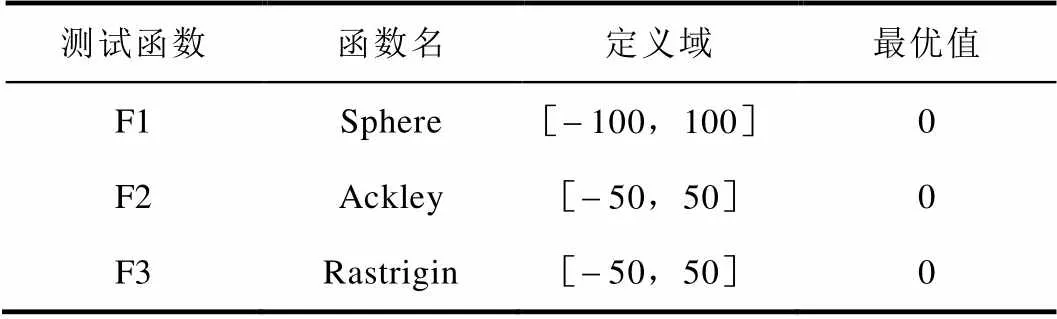
表2　测试函数

由于算法的随机性，取100次计算结果的平均值，验证结果如表3所示。

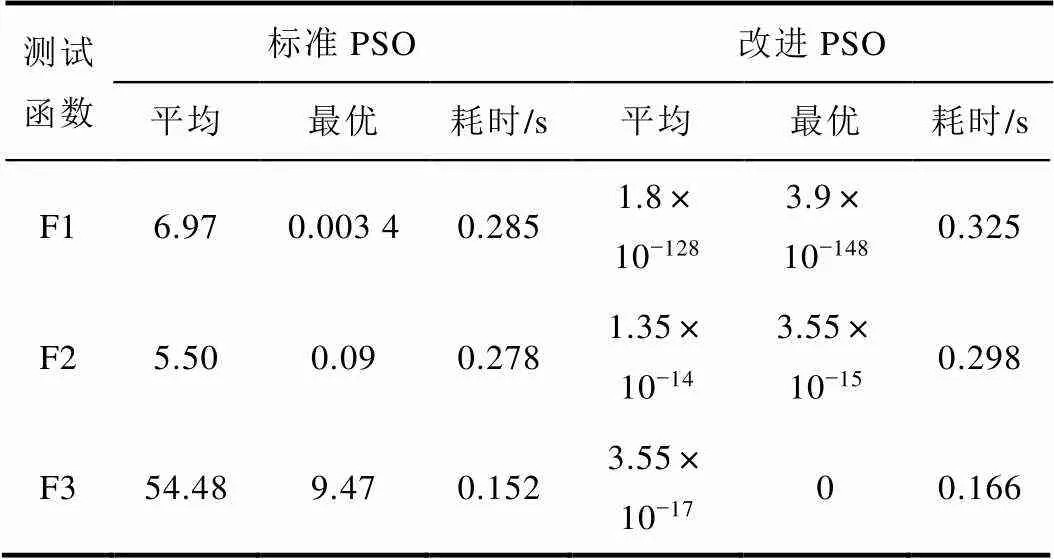
表3　算法验证结果

从表3可知，改进PSO算法的适应度函数平均值和最小值都远远小于标准PSO算法，可见改进PSO算法的收敛精度要高出许多。另外，虽然改进PSO在标准PSO的基础增加了算法的复杂度，但是在同一测试环境下改进PSO的计算量并没有明显的增加，而且两者的所耗时间都很小。以上结果说明改进后的PSO符合实际应用中对准确性和实时性的要求，为后面的算法引用提供了支撑。

3　广义预测控制算法及其改进

针对SG液位中出现的时变、“虚假液位”以及输入约束等复杂控制问题，为了改善控制效果，在常规GPC算法的基础上，对预测模型、滚动优化和在线校正三个基本环节进行相应地改进设计。

3.1　预测模型

在SG液位控制系统中，SG的液位受给水流量和蒸汽流量的共同作用，其中，给水流量是可控量，蒸汽流量是可测但不可控量，因此需要不断调整可控量，用于克服不可控量对系统输出的影响，使系统输出具有期望的动态特性。因此，通过引入蒸汽流量干扰项，构建如式（4）所示的双输入单输出模型来描述SG液位系统：

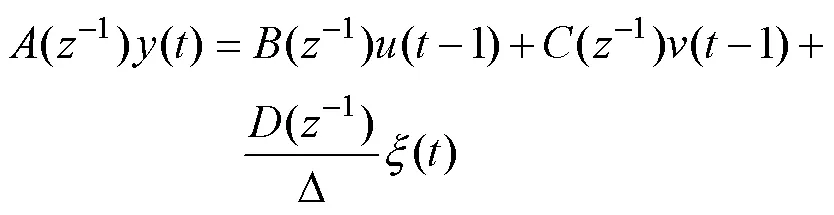
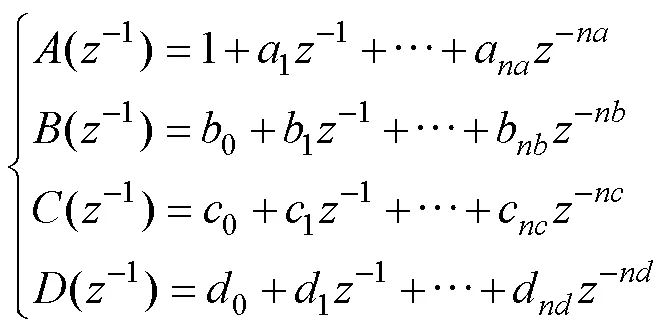
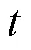
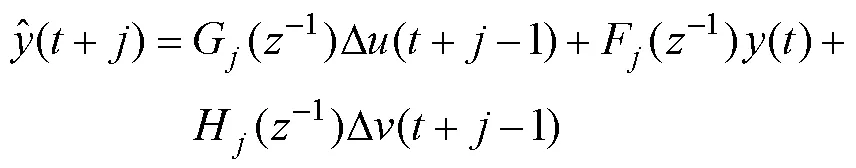
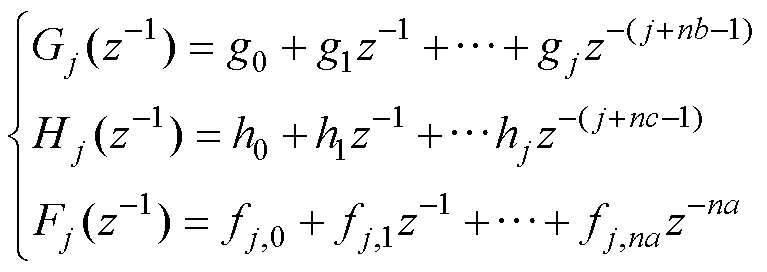
3.2　滚动优化

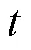
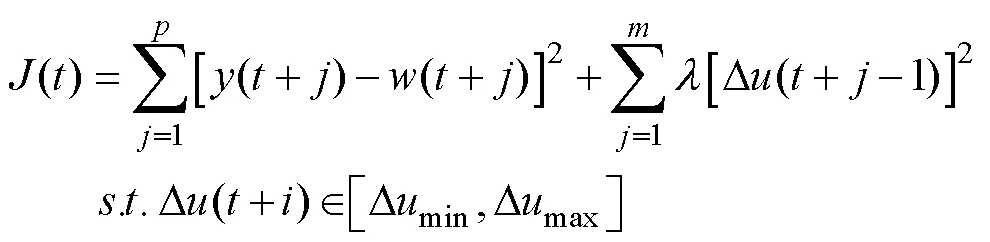
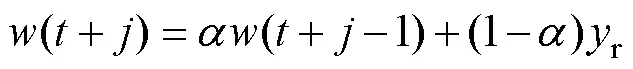
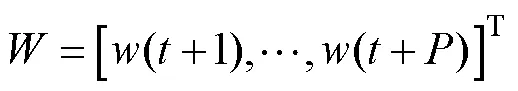
将式（6）预测模型中的未知部分和已知部分进行分离，可以得到：

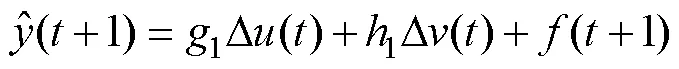
其中：

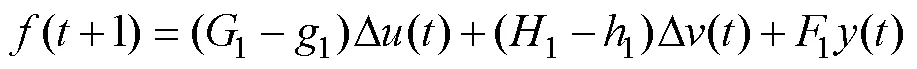
同理可得：

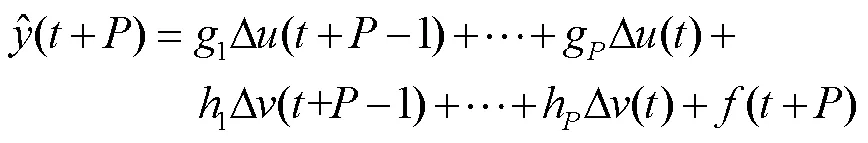
其中：

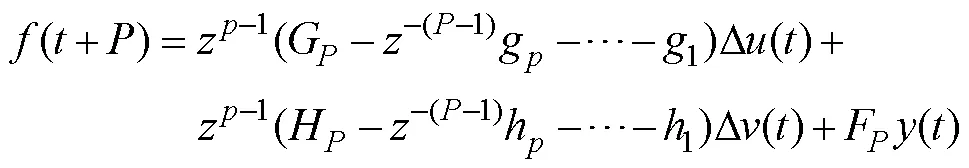
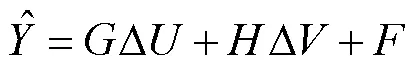
式中：

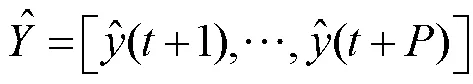
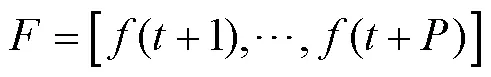
对于（8）中的性能优化函数，用预测输出代替实际输出，并引入式（10）和式（13）可得到如下向量形式的性能优化函数：

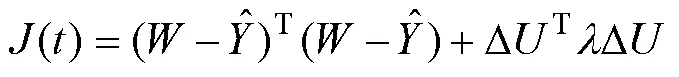
3.3　在线辨识与校正

在实际运行中，SG液位系统会随着时间和工况的改变而发生变化，对此，需要通过实际输入与输出信息在线辨识对象模型参数，从而给出准确的预测来修正控制作用，保证良好的控制效果。由于输入输出的数据量会不断增加，为了充分利用最新的数据，在这里采用变遗忘因子的递推最小二乘辨识算法进行在线辨识。

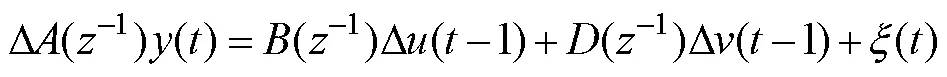
继续推导：

令：

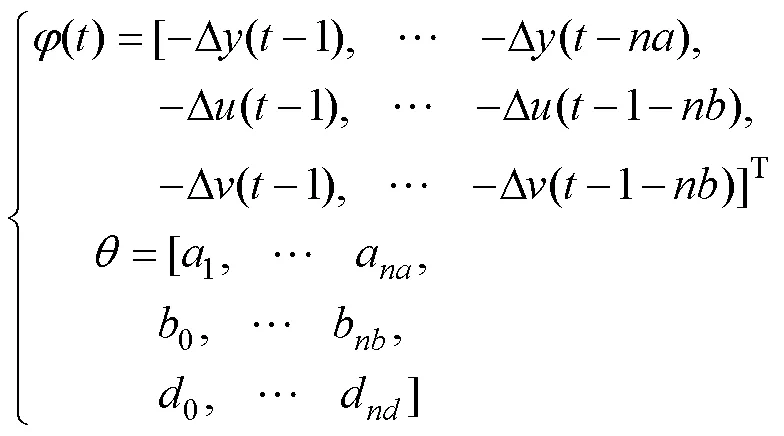
可得：

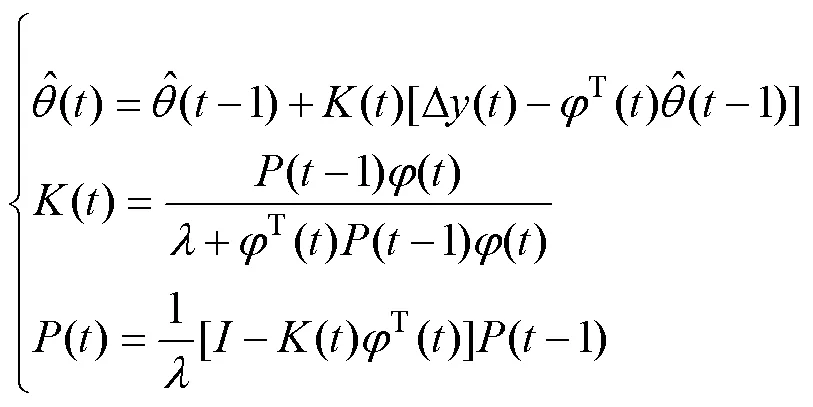
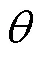
3.4　改进广义预测控制的算法步骤

（1）初始化参数，构造式（4）对象模型；

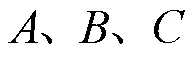
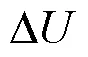
（5）转至步骤2重复进行在线辨识和滚动优化，直到控制系统结束工作。

4　仿真验证

为了检验所提出的改进GPC控制算法能否有效地解决 SG液位控制中的复杂问题，进行了如下仿真。仿真过程中液位设定值在运行功率低于20%时取945 mm，运行功率处于20%至100%时取1 047 m[13]。

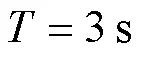
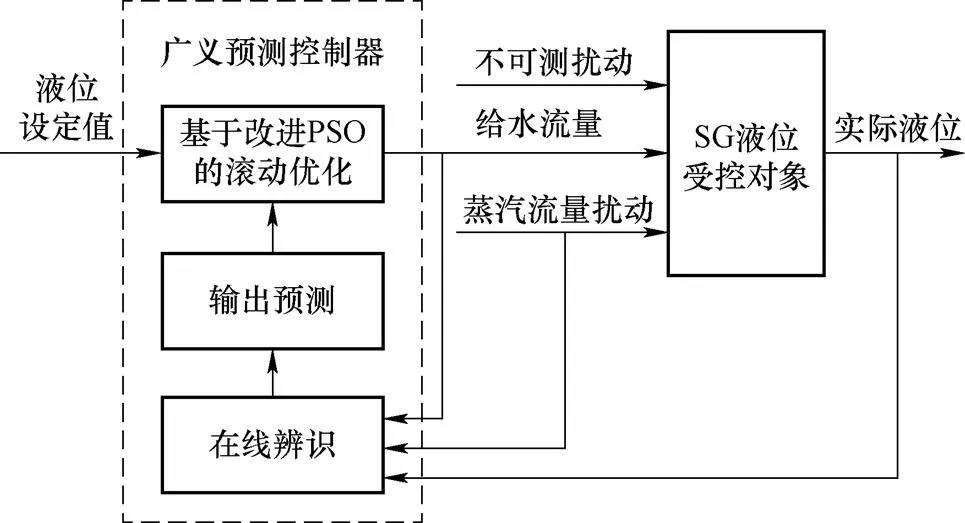
图2　改进GPC控制框图

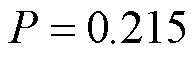
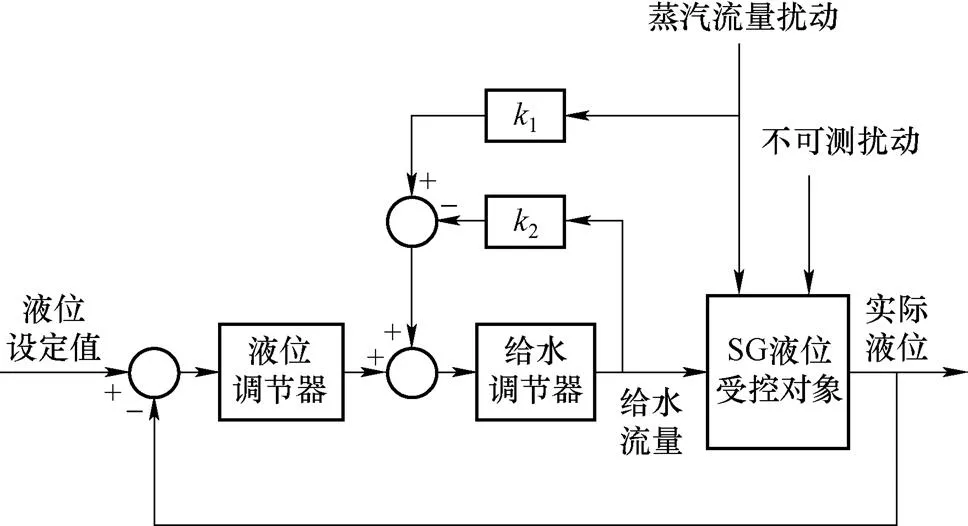
图3　三冲量PID控制框图

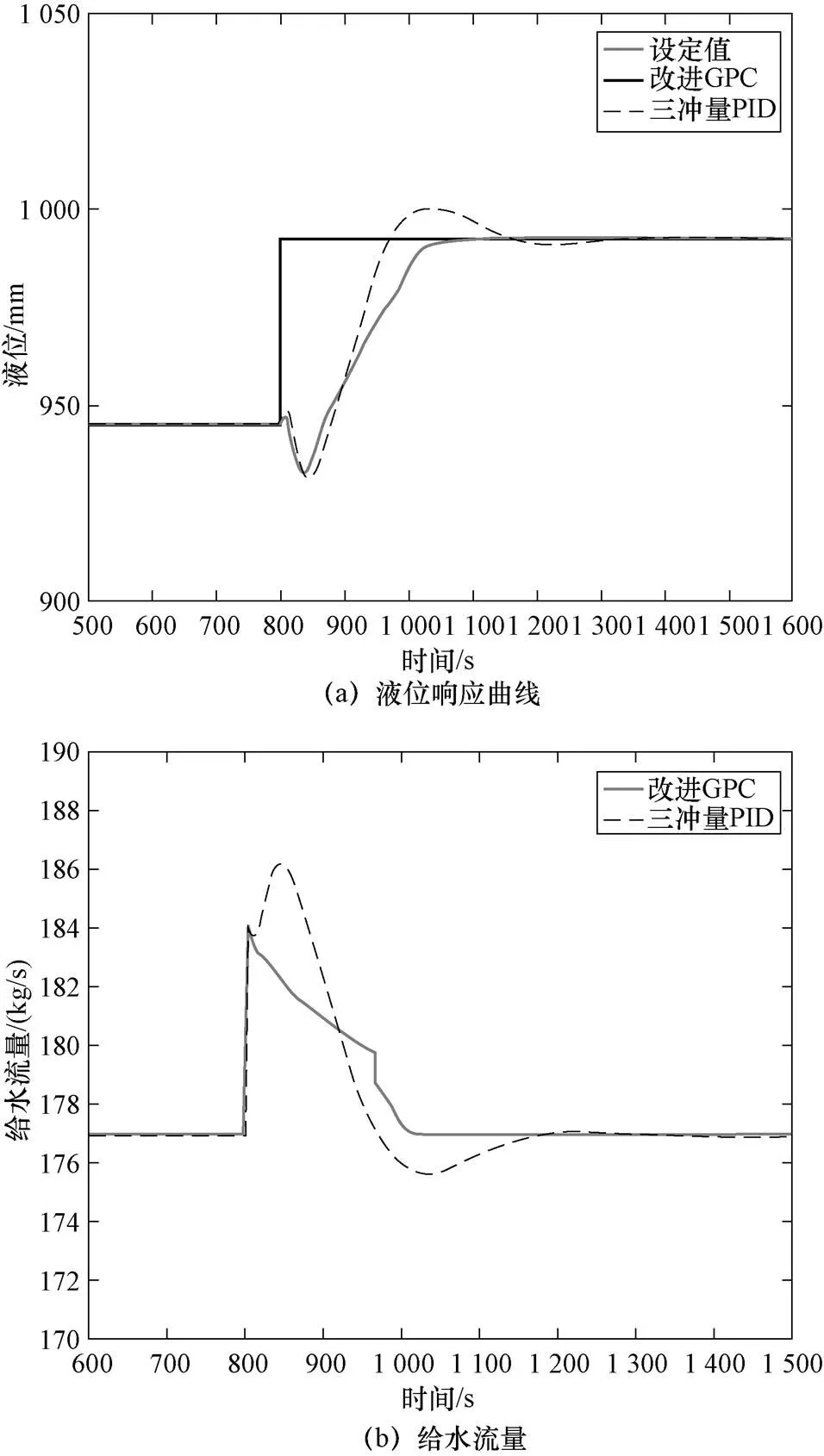
图4　液位设定值扰动控制效果图

从图4（a）可以看到，在液位设定值出现扰动后，改进GPC控制器经过243 s左右调节后便趋于稳定，而三冲量PID控制器的调节时间较长，约为348 s，且最大液位超调量达到14.1 mm，但两者在液位初期的最大下降量相差较小，仅有1.25 mm。从图4（b）中可以看出，相较于三冲量PID控制器，改进GPC控制器给水流量的变化幅度更小，能更快地趋于稳定。因此，在设定值发生扰动时，改进GPC比三冲量PID有着更好的稳定性和快速性。

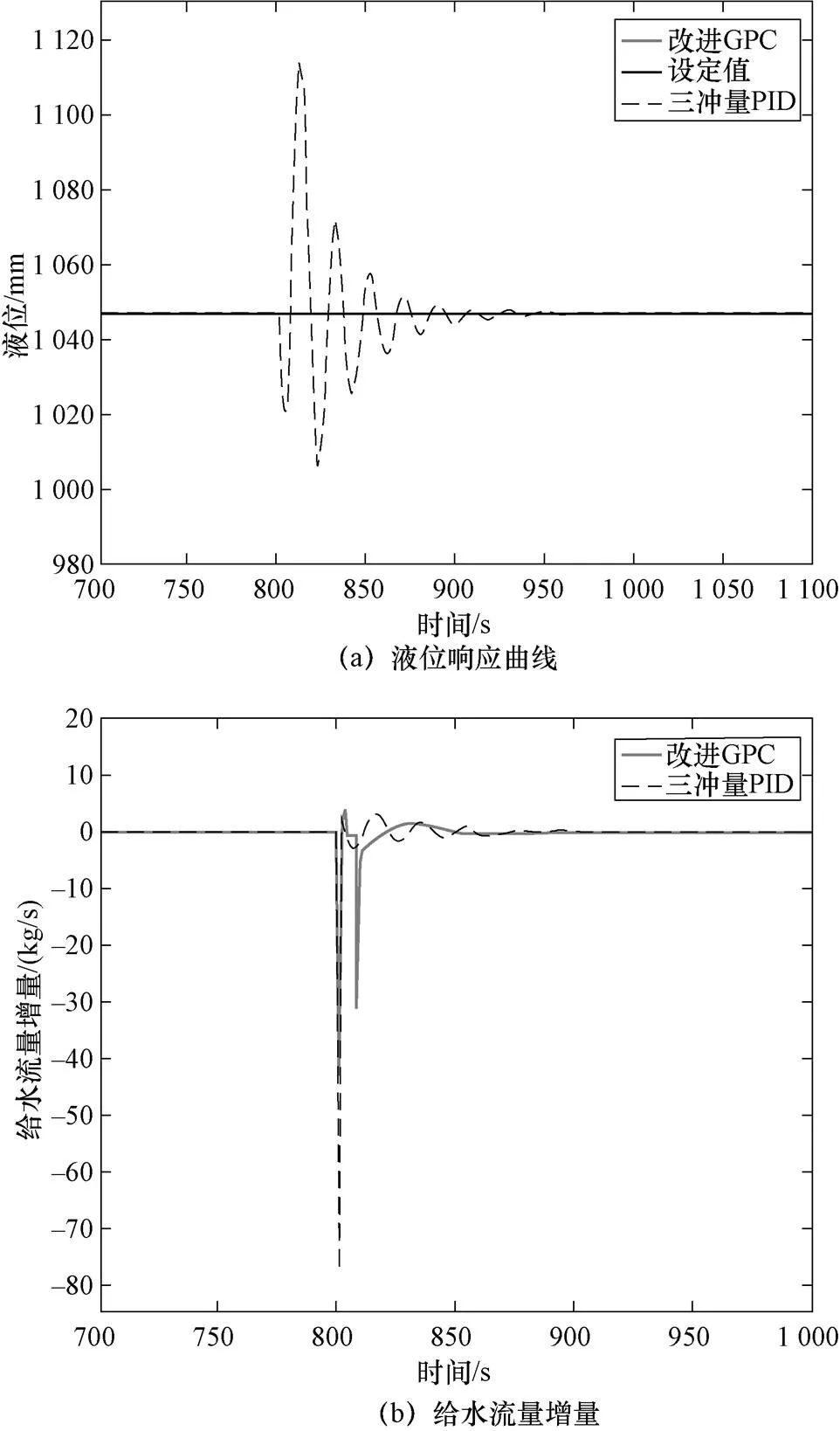
图5　蒸汽流量扰动控制效果图

从图5（a）中可以看到，当蒸汽流量出现扰动后，改进GPC作用下的液位波动比较稳定，最大超调量为40.5 mm。而采用三冲量PID控制器时，液位的变化幅度较大，最大超调量达到66.5 mm，调节过程中还出现了连续振荡的情况。从图5（b）中可以看到，改进GPC控制器的最大控制量增量比三冲量PID控制器大约低35.9 kg/s，变化更加平缓。因此，在蒸汽流量发生扰动时，改进GPC控制器在一定的约束范围内，比三冲量PID控制有着更好的抗干扰能力，能够快速地趋于稳定

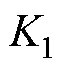
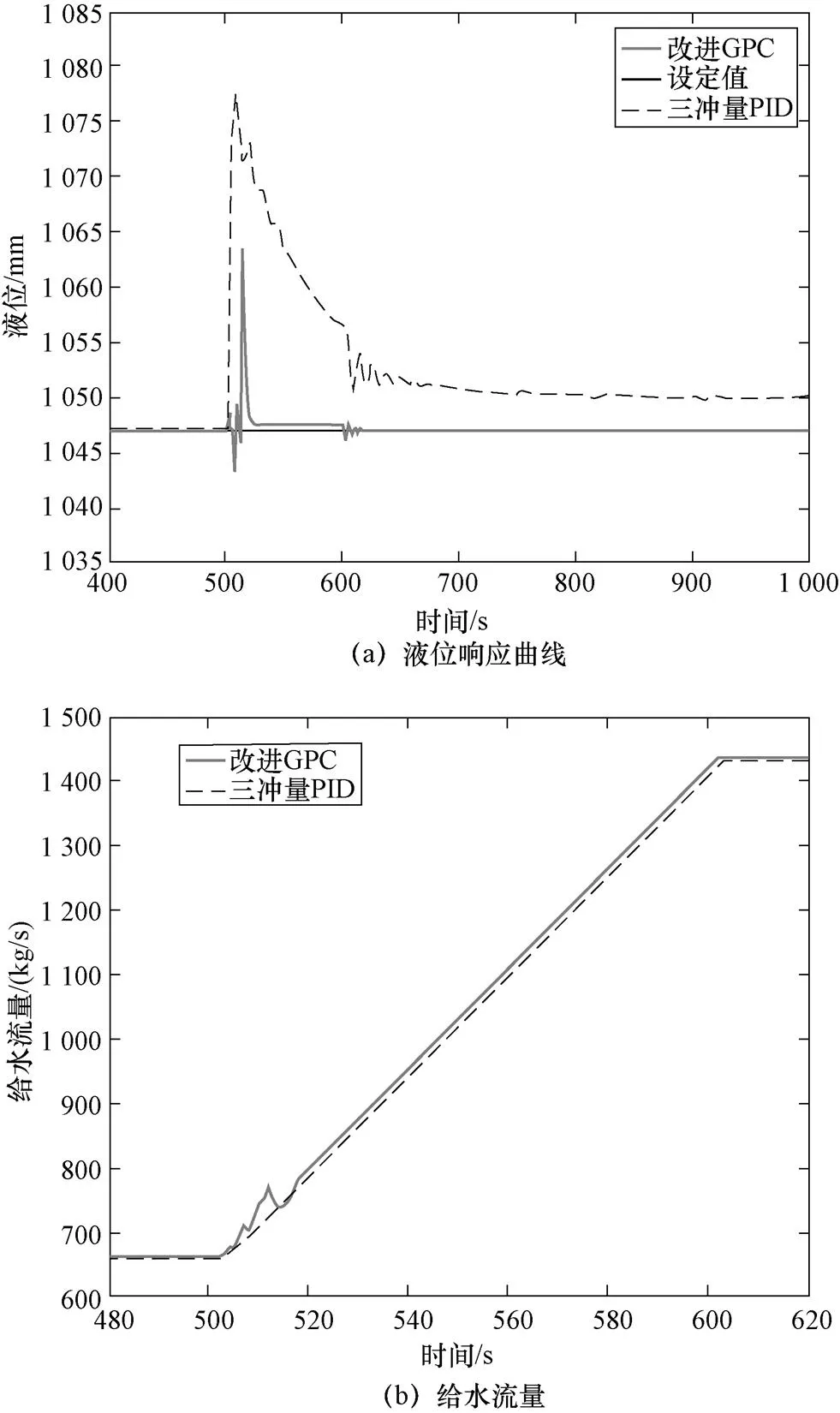
图6　变功率控制效果图

从图6（a）可见，当运行负荷发生变化后，三冲量PID控制的SG液位产生了大幅度波动，最大超调量大约为29 mm，并且出现了3.2 mm的稳态偏差，相比之下，改进GPC控制下的SG液位波动较小，最大超调量为16.5 mm，并且没有稳态偏差。图6（b）可以看到，改进GPC控制器作用下的控制量在负荷变化后迅速地进行调整，在扰动初期产生了微小的波动，但是三冲量PID控制器由于没有自适应功能，没有进行及时地调整。所以相比三冲量PID控制，改进GPC算法在运行负荷发生改变时的控制效果更好，自适应能力更强。

5　结论

对于压水堆核电站中蒸汽发生器存在的液位控制难点，本文在常规广义预测控制的基础上，做了如下改进工作：

（1）引入了两输入单输出的SG液位对象数学模型，能够针对蒸汽流量的扰动进行抑制，改善了蒸汽流量扰动产生的“虚假液位”现象，提高了SG液位控制系统的稳定性；

（2）引入了改进粒子群算法在约束范围内计算最优给水流量增量，使得实际的水流变化更加均匀，增加了算法准确性的同时减少了计算量；

（3）引入了带遗忘因子的递推最小二乘算法进行在线辨识，保证了SG液位数学模型的精度，调高了SG液位控制的自适应性。

通过与传统三冲量PID控制的仿真结果对比，验证了上述改进措施的有效性，为压水堆核电站的蒸汽发生器液位控制系统提供了一种理论优化方案。

［1］ 苟晓龙，张宏亮，张龙强.CPR1000/EPR/AP1000蒸汽发生器液位控制系统对比分析［J］．核科学与工程，2011，31（S2）163-169.

［2］ Mayuresh VK，Mettler B，Morari M，et al.Linear Parameter Varying Model Predictive Control for Steam Generator Level Control［J］．Computers Chem Eng，1997，21：861-866.

［3］ 袁景淇．压水堆蒸汽发生器水位的前馈模型预测控制［J］．控制工程，2008，15（3）：250-252.

［4］ Parlos AG，Parthasarathy S，Atiya A.Neuro-predictive Process Control Using On-line Controller Adaptation［J］．IEEE Transactions on Control Systems Technology，2001，9（5）：741-755.

［5］ 周刚，彭威，张大发．核动力蒸汽发生器水位控制方法分析［J］．原子能科学技术，2004（S1）：19-23.

［6］ Clarke D W，Mohtadi C，Tuffs P S.Generalized predictive control：partⅠthe basic algorithm［J］．Automatica，1987，23（2）：137-148.

［7］ Irving E，Bihoreaux C.Adaptive control of nonminimum phase system appli-cation to the PWE steam generator［C］．19th control and decision Conference，Albuqu-erque N.H：USA，1980:11.

［8］ 邱磊磊．自然循环蒸汽发生器的水位动态特性分析［J］．核动力工程，2021，42（S2）：5-9.

［9］ Kennedy J，Eberhart R.Particle Swarm Optimization［C］．Piscataway，NJ，Ⅳ：IEEE International Conference on Neural Networks（Perth Australia），IEEE Service Center，1995:1942-1948.

［10］Rahnamayan S，Jesuthasan.Computing opposition by involving entire population［C］．IEEE Congress on Evolutionary Compu-tation（CEC），2014:1800-1807.

［11］罗强，季伟东，徐浩天．一种最优粒子逐维变异的粒子群优化算法［J］．小型微型计算机系统，2020，41（02）：259-263.

［12］葛宝林，林飞，李国国．先进控制理论及应用［M］．北京：机械工业出版社，2012:117-122.

［13］欧阳予．秦山核电工程［M］．北京：原子能出版社，2000:291-293.

Study on Liquid Level Control of the PWR Steam Generator Based on Constrained Adaptive GPC

YE Zhanglin，ZHANG Yufei

（Southeast University School of Energy and Environment，Nanjing of Jiangsu Prov.210096，China）

In PWR nuclear power plant, whether the liquid level of the steam generator can be stably controlled within the set range is directly related to the safe and economic operation of nuclear power plant. Aiming at the complex problems of “false liquid level”, time-varying and input constraints in steam generator liquid level control, an adaptive generalized predictive control algorithm with constraints is designed. In this algorithm, a two input single output mathematical model is constructed to describe the influence of steam flow and the feedwater flow on the liquid level of steam generator; The minimum recursive multiplication with variable forgetting factor is introduced to identify and correct the parameters of the liquid level object model of the steam generator on line; The mutation strategy of inverse learning of the center of gravity per dimension is introduced to improve the convergence accuracy of the standard particle swarm optimization algorithm, and then the improved particle swarm optimization algorithm is used to calculate the optimal value of the feedwater flow increment within the constraint range. The simulation results show that the improved generalized predictive controller has better control effect than the three impulse PID controller for the complex control problem of steam generator liquid level.

Steam generator；Level control；Generalized predictive control；Two input single output；Online identification；Particle swarm optimization

TP273

A

0258-0918（2022）06-1345-09

2021-10-25

叶章林（1997—），男，湖北荆州人，硕士研究生，现从事压水堆核电站蒸汽发生器液位控制方面研究