加收计费，加在哪里、收在何处

张志梅

[摘 要]小数乘法部分内容，分段收费是一个必备题型，它能有效训练学生的小数计算水平，并编设了整数乘法和小数乘法的混合运算，但是，分段计费问题中的“加收”一词语意不明，在不同的问题情境中掺杂不同营销话术可能会引起不同解读。

[关键词]歧义;语境;分段;小数;乘法;加收;单价

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2022）02-0024-03

在教学人教版教材五年级“小数乘法”课后的解决问题时，经常会出现收费问题，这类问题中的经典提问是，超过“起步价”后，每增加一项服务内容，就要按另外的标准收取费用，这就是所谓的加收问题。每次遇到“斤斤计较”的账目问题，师生都会头大，尤其是这样的分段收费。消费到了不同级别，会出现不同的收费标准，解决这样的加收问题，往往要顾及前一阶段的收费情况，因此变得异常复杂，这也引起了年级组教师的激烈争论。对于分段计费的具体算法，大家存在很大的分歧和争议，难以统一意见。这样造成的后果是，教师按照各自的理解去教学和去评判的学生作业，导致同一个学校出现不同的阵营，不同班的学生接受到的加收方法不同。那么，像这样的加收问题，到底该遵循什么标准和原则，形成“天下一统”的局面呢？

一、新版例题的歧义

在新版教材第18页的“举一反三”作业练习中，出现如下所示的例题习题。

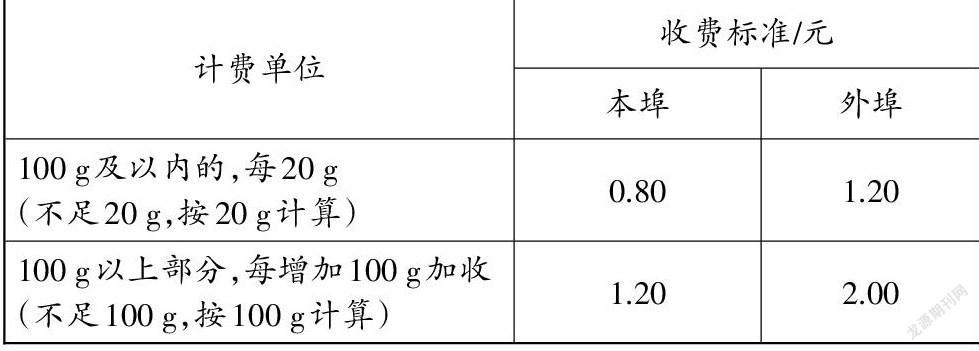
邮局邮寄信函的收费标准如下表。

（1）小亮寄给本埠同学一封135 g的信函，应付邮费多少钱？

（2）小琪要给外埠的叔叔寄一封262 g的信函，应付邮费多少钱？

（3）你还能提出其他数学问题并解答吗？

在邮局邮寄信函的收费标准中，其中“100 g以上部分，每增加100 g加收（不足100 g，按100 g计算）”，这里第一次出现了“加收”的描述。对于“加收”一词，该如何理解？笔者认为这个词有点令人费解，到底是指在第一段收费之外增加的第二段收费，即“加收”单指增加新一阶段的收费，还是指超标部分单独增加单价，加收具体是指单价的累加？所谓“加收”， 网上的词条显示是在原来已有收费的基础上另行增设收费项目，也就是附加的收取的钱。又据《教师教学用书》对教材的解析，以及提出的教学建议，本题型属于分段计费的题型，题目的本意是让学生计算分段计费，按照不同的分段标准和对应的计费方式核计费用。这里麻烦的是，除了设立分段标准和界限，还要区分本埠和外埠两种并立的收费方案。那么按照《教师教学用书》的指示，这类题型的重点是分段计费，那么“加收”一词指的应该是增加第二阶段收费，而不是增加单价，此处的“加”，意指在算出第一阶段费用后，要加上第二阶段费用，才是邮费总额。

数学是一门严谨的学科，其严谨性不只体现在数据的精确、计算的准确，还体现在语言表达上的严密，对某些概念的表述，必须达到精准、简练的地步。但是，由于汉语言的灵活性和丰富性，存在一词多义和一语双关现象，有的语句在特定的环境下可以作特殊的解读，这是汉语言的特性。如分段计费中的“加收”一词，到底是超过“起步价”后的超额部分单独“加价”，还是针对这一部分另行计费，这是值得商榷的。但是就数学教学的经验和教学目标以及所处的学科氛围综合考量，不难推测，小学阶段分段收费问题中的“加收”，应该是对超出基础的部分单独制订收费标准，也就是说与第一段的收费严格区分开，这就暗合了中学阶段的分段函数。如果用函数思想来理解这个问题情境，就会发现这一课程的目标在于培养学生分类讨论、分段整理数量关系的能力，在基础部分，按照基础部分的计价方式收费，收满第一阶段后再对超出部分另外收费，而不是重复收费。

二、原版例题的表述

教学中，教师不仅要训练学生分析问题、判断形势、做出决策、确立标准、计算费用的能力，还要培养学生运用规则、创设情境、提出问题的能力。因为有旧版教材第十二册的类似题型作对比，如果以原题为参照和借鉴，那么本题的题意不存在歧义，只有唯一的通识理解。解决方法如下。

调查邮局邮寄信函的收费标准：首重100 g及以内的（不足20 g，按20 g计算），每20 g收取定额费用，其中本埠0.80元/20 g，外埠1.20元/20 g;续重101～2000 g（不足100 g，按100 g計算），本埠1.20元/100 g，外埠2.00元/100 g。

（1）李华要寄一封不足20 g的信函给本埠的舅妈，应付邮费多少钱？

解：因为这是寄到本埠的信函，且信函不足20 g，所以按照首重的收费标准，李华应付0.80元邮费。

（2）刘明要寄一封45 g的信函给外埠的姑妈，应支付邮费多少钱？

解：因为这是寄到外埠的信函，45 g<100 g，所以按照首重的收费标准，45÷20≈3，刘明应付1.2×3=3.6（元）邮费。

（3）张叔叔寄给本埠的表姐一封135 g的信函，应付邮费多少钱？

解：100÷20×0.80=4（元），（135-100）÷100≈1，4+1×1.20=5.20（元）。

（4）李大妈要给外埠的表哥寄一封262 g的信函，应付邮费多少钱？

解：100÷20×1.20=6（元），（262-100）÷100≈2，6+2.00×2=10（元）。

原版的表述，直接出示超出部分的单价是多少，不仅绕开了“加收”一词，有效避免了歧义，而且对第二阶段的计重，也明确指出计重范围为101～2000 g，而不是笼统地说超出部分，因此语意非常明确，就是超出部分单独计费。

再来看《长江作业本》第10页的第2题：

联通公司为了拓展移动通话业务，重新调整了战略布局。为了鼓励联通用户办理4G网络漫游套餐订购服务，常州市联通分公司对联通手机用户每月的手机流量收费标准作了下调：用户每月流量不超过20 G的，每G收费25元;超过20 G的部分，每使用1 G加收5元。

（1）李总5月份使用手机流量为11 G，应缴流量费用多少元？

（2）刘总5月份使用手机流量27 G，应缴流量费多少元？

解：（1）11×25=275（元）;（2）20×25+（27-20）×（25+5）= 710（元）。

本题由于受到联通公司相关资费套餐的宣传影响，以及长期以来人们对流量收费的惯有认识，故此处的“加收”含义非常明确，指向性非常强。因为手机流量的稀缺性，以及收费较高，所以在超出一定额度后，流量的单价就会提高，不可能会降低，所以此处的加收是指在原有收费价格的基础上提价，作为加收部分。比如，此处的加收5元，实际上就是每G流量涨价25%，也就是每G流量费用由原来的25元涨至30元，这是常见的商业术语。再加上“加收5元”，5元远小于25元，个人超额使用流量，抢占了其他用户的流量配额，所以理应根据市场规律涨价，也就是所谓的市场调节，通过价格杠杆，达到用户自觉限流的目的，所以5元不可能是超额部分每G流量的单价，而应该是附加在原价基础上的25+5=30（元）。正因如此，此处的加收才不会受到日常表述的影响，“加收”一词符合客观实际和商业语境。

不同的表述会带来不同的理解，词语的生活含义和数学含义有时是一致的，有时又存在出入。如“加收”一词无论怎么理解都会带来歧义，在生活中和数学中皆是如此，但是换成一个新词“续重”，那么语境就会大不相同。“续重”一词多见于邮政、快递、海关、托运等称重计费服务，一个“续”字洗练传神地表达出这是超出基础重量的重量，既然作此理解，那么后面提到的收费当然就是针对续重部分的单独计价，与前面的基础重量在“量”和“价”上划清界限，互不交叉、互不干扰，从而有效避免了“加收”一词带来的歧义。而即使是“加收”一词，在某种特定场景下，也可以暗指在原有基础部分的单价上提高单价，也就是“涨价”的代名词，如移动流量费、停车服务费、房产税、车船购置税、包厢使用费、燃油附加费等，这些公共稀缺资源一旦被超时、超额、超量占有，就需要个人加倍付出费用。

三、例题中的歧义辨析

继续看《长江作业本》第11页的第3题：

明明来到气步枪射击训练场，射击了8次标靶，你知道他此次射击游戏的总花费是多少吗？价格表：35元射击5次，超过5次，每射击一次加收3.5元。

对价格表中“35元射击5次，超过5次，每射击一次加收3.5元”这句话，教师形成两种意见。一种意见认为根据累加计费原则，前一段是一种收费标准，后一阶段是在前一阶段的基础上叠加，前5次是一个阶段，单价为每次7元，超过5次的部分则单价增加，每射击一次加收3.5元，此处的加收意指累加收费，也就是按照每次（7+3.5）=10.5（元）的新标准收费，顺承前一阶段的收费，即5 次后每次射击收10.5元，10.5×3=31. 5（元），所以本题的解为7×5+（8-5）×（7+3.5）=66.5（元）。

而另一种意见则坚持认为35元射击5次，是起步价，即射击5次是35元，射击4次、3次甚至2次、1次也是35元，只要开始游戏，就必须先缴纳35元。超过5次后费用较高，为了促销，商家推出优惠活动，单价有所下降，这符合一般的商业运作规则，同时也是商家的惯用伎俩。于是，超过5次后，单价降至每次3.5元，所以本题的解应为35+（8-5）×3.5=45.5（元）。

在这种各执一词的局面下，双方似乎都有道理，那么问题的焦点来了：这里的“加收”和“收”字是一个意思吗？如果是一个意思，那么为何多此一举绕弯子说“加收”呢？直接说收取不更直截了当吗？如果不是一个意思，那么加收就应该是在原价的基础上提高单价，也就是现价是在原价基础上加价，这样原价就应该用7元/次的表述，明码标价，而不是含糊其辞说5次以内收取35元。只有标明原价，加价才有基础。还有，如果是在原价的基础上“加收”，那么这个游戏就是越玩费用越贵，这无疑是不利于商业经营的，也不符合常理。

当然，尽管数学表达必须严谨，但是除了纯理论化的定理法则表述，一般与生活相关的概念表述放在具体的生活情境中，都脱离不了生活气息，有时还得到当时当地的场景中还原，针对社会活动中行为人的正常心理，也就是一般大众心理，联系人之常情来揣测关键词的意义。如在这个射击游戏中对“加收”的理解，如果不是提高单价，为什么要说“加收”而不直接说“收”？首先，从人之常情来理解，这个射击游戏不属于稀缺的公共资源，它和汽油、柴油、车位是有本质区别的，它属于可以无限次使用的过剩资源，一个玩家少射击几次和多射击几次对射击场没有影响，或者说影响很小，可以忽略不计。相反，如果玩家射击的次数过少，反而是一种浪费，玩家必须玩到一定量，商家才能回本，资源才算不被浪费。因此，玩家射击5次或以内，必须缴纳35元，这个35元就是成本价，也可以理解为保护资源的最低成本，超出部分“加收”中的“加”字，是指超出“起步价”包含的最大服务容量后，追加收费。

综上所述，在分段计费模型中如何理解“加收”一词，既要考虑到数学的严谨性，又要考虑到生活实际的合理性，因为这个问题本身就是一个与生活实际密切相关的数学模型，而不是一个高度抽象的數学理论，入情入理灵活处理才是根本。

[ 参 考 文 献 ]

[1] 李旭.且行且思，让计算教学绽开智慧之花[J].小学教学参考，2020（32）.

[2] 黄朝峰.如何理解小数乘小数的算理？[J].福建教育，2020（40）.

[3] 王卉.立足经验 “理学”融通[J].小学教学研究，2020（26）.

[4] 朱峰.从已知出发探索前行 [J].小学数学教育，2020（Z4）.

[5] 黄世贵，刘贤虎.基于问题串  从浅层走向深度[J].中小学教学研究，2021，22（04）.

（责编 吴美玲）