静态分析和比较静态分析中的拉格朗日乘子法
杨卫涛
(1.开封大学 a.财政经济学院;b.区域经济研究所,河南 开封 475004)
一、引言
拉格朗日乘子法在高等数学的微积分下半部分出现,描述的是带有等式约束条件下目标函数的极值问题。现实生活中,约束无处不在,而且人们总是在这些约束中追求某种最大化(利)或最小化(弊),即使是中华传统文化中不追求极大或极小等极端情况的“中庸”思想,其实也可以用“鞍点”理论来描述。一个马鞍,我们可以从不同的角度来看它。鞍点,既包含极大值,也包含极小值。中国人主张兼容并蓄。“鞍点”理论与中国处世哲学相符。
为了便于几何可视化和对概念的理解,将本文的所有函数均设定为二元函数,并且极值问题探讨以取极大值为例,极小值同理可得。带有等式约束条件,将目标函数最大值问题描述如下:
该问题的文字描述是:变量(x,y)在满足 g(x,y)=m 的条件下,取何值时能够使目标函数 f(x,y)达到最大值?这种问题的一般解决方案是,利用拉格朗日乘子组建方程:
然后,对上式关于变量(x,y)和λ分别求一阶偏导并且为零,解三个方程即得结果。为什么要采用这种奇怪的形式来求解?这一问题始终困扰着学生。讲清楚这个问题,对后续的学习至关重要。
对以资源有限稀缺为生存前提的经济学来说,稀缺就是约束。可以说,约束贯穿整个经济学,是这个经济学的逻辑主线[1]。因此,不掌握这个带有约束条件的问题,进行更深入的经济学研究很困难,可谓寸步难行。不同语言或学科之间互相借用,有时候可以精练描述所传达的信息,正如爱因斯坦用数学公式E=MC2精练表述,为我们打开了核能世界的大门。我们所面对的现实经济世界中,每天都有无法摆脱但又是必不可少的各种各样的约束。本文借用英文单词tyranny来传达含义。
静态分析和比较静态分析是经济学中两种常见的事先设定的“生态环境”,里边的物种就是变量[2]。内生变量和外生变量处在这两个环境中,由我们根据研究目的和要求自行设定。内生变量是在设定的经济生态环境中“自生自灭”的,外生变量是设定的经济生态环境中的外来物种,一般初始设为不变的。简单来理解,静态分析是在外来物种(外生变量)不变的情况下,寻找经济系统的均衡状态(类似生态平衡)。比较静态分析是找出在外来物种(外生变量)变动或扰动的情况下,经济系统均衡状态的变化情况[3]。因此,将各种经济因素设定为数个变量。一般地,将短期内基本不变的设为外生变量,将容易受干扰且易变的设为内生变量。各种经济因素之间的关系和约束条件用等式和方程组来表示。然后,作静态分析和比较静态分析。根据一般的意思来理解,有静态就有动态。动态分析中有两部分内容:变分法和动态最优化。变分法用到的是广义的拉格朗日乘子,动态最优化中用到的是汉密尔顿乘子。虽然研究前提和环境发生了本质变化,但与本文的拉格朗日乘子法表达形式类似,由此可见,拉格朗日乘子法是重要的基础和桥梁。
二、拉格朗日乘子法
要了解拉格朗日乘子法的来历,就需要用到向量、定义在向量上的运算这些概念。
(一)自由向量
向量,自高中开始学起。进入大学以后,任何一本高等数学或线性代数教材(难度稍高的比如高等代数、复变函数等领域的教材)中都有向量的定义和详细含义讲解。向量的灵魂是自由向量,没有它,向量只是二维或三维甚至高维图中的一些点而已,完全失去了向量的魅力,也限制了向量释放巨大能量,缩小了其施展拳脚的空间。向量可以用从坐标原点出发指向终点的有向线段表示,也可以用点值来表示。向量具有“点”“线”二象性,既可以看成有向线段中指向终点的“点”,也可以看成一个具有方向的线段。自由向量则摆脱了原始向量的定义,利用向量的特征(有向线段),将所有的方向相同和长度相等的向量视为同一个向量,并且很容易用几何或代数形式证明。如图1中的有向线段,方向相同且长度相等,因此在同一坐标系中视为同一个向量。这就意味着,一个向量,在同一坐标系中任意平移,向量的属性保持不变。这就是它叫做自由向量的原因。
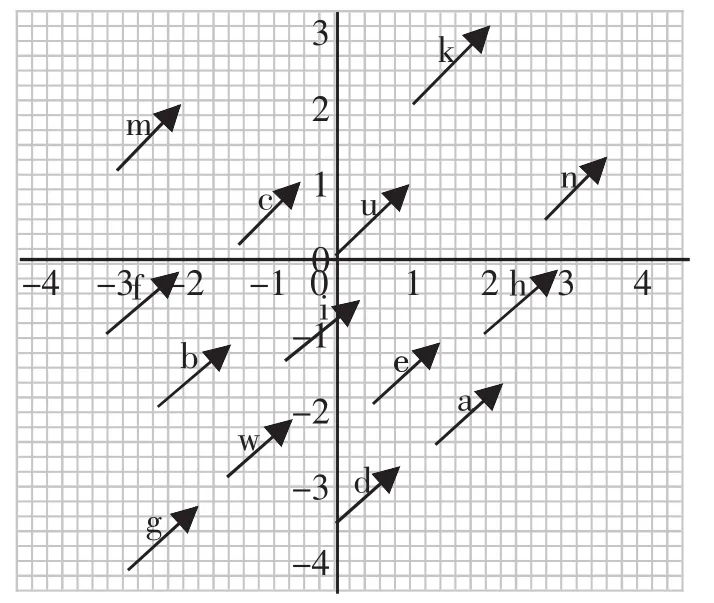
图1 方向相同且长度相等的自由向量
(二)定义在向量上的运算
为便于学生理解,我们用二维平面上的点和线段组成的运动轨迹,来描述定义在自由向量上的运算符号所表示的含义。定义在向量上的运算很多,讲清楚本文所介绍的拉格朗日乘子,只需要加法、数乘和内积运算。
1.加减法运动轨迹规律
在向量上定义的加法,基础知识不再赘述。以a,b,c,d,e,f,g这7个自由向量为例,仅说明向量加法的运动轨迹规律。如图2所示。

图2 向量加法的运动轨迹规律
我们看向量加法体现的“点”“线”二象性。类似接龙游戏:a由原点出发,沿着后续b,c,d,e,f,g的有向线段的路径前进,最后到达终点。减法是加法的逆运算,b到g的路径,180°旋转调头,沿着这样的路径前进。如图3所示。
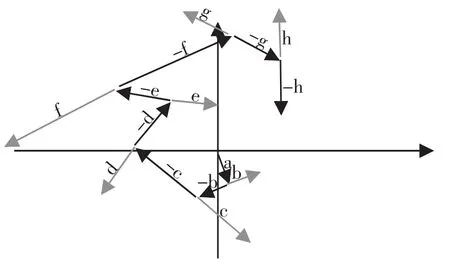
图3 向量减法的运动轨迹规律
2.数乘运动轨迹规律
数乘运算很简单,反映在几何图形上,就是向量(有向线段)的拉长和缩短。本文仅描述两个向量的凸组合运动规律。a,b是两个向量,我们取其“点”性来描述凸组合[4]P28-32。

图4 向量的凸组合运动轨迹规律
当0≤λ≤1时,λa+(1-λ)b就表示在点a和b之间的线段上滑动。λ=0时与b点重合,λ=1时与a点重合。
3.内积
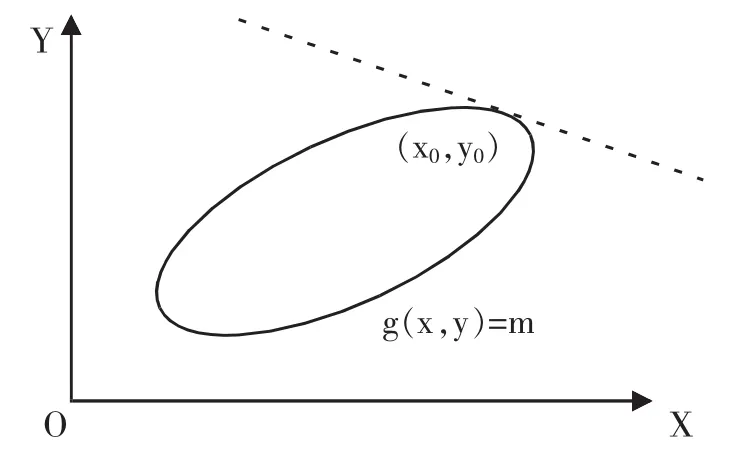
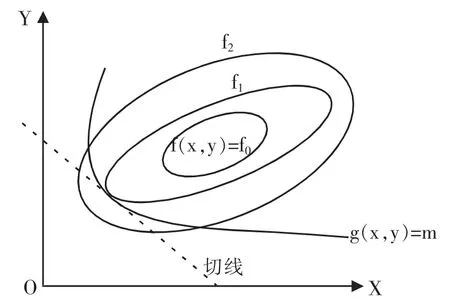
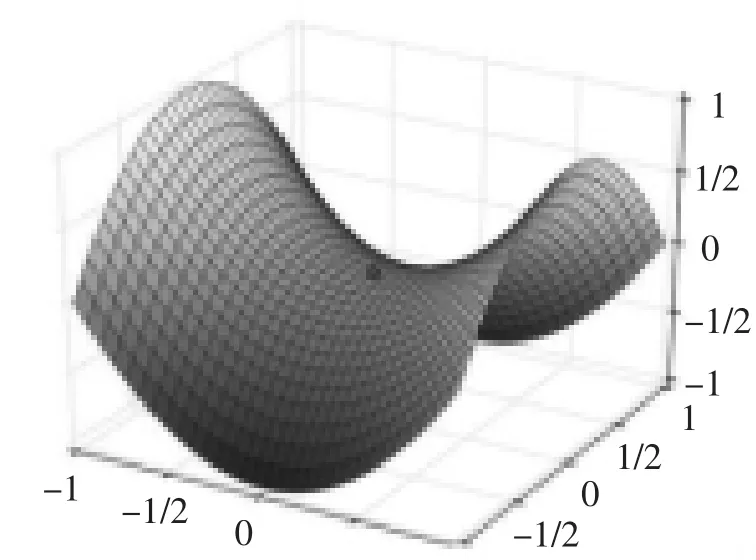
仍以二维几何平面为例。两个向量 a=(x1,y1)和 b=(x2,y2),两向量内积表示为 图5 b沿a方向的“高度” 4.切向量与法向量 切线,在中学阶段就开始接触,在大学阶段,又重拾且加持,微积分、空间解析几何、微分方程都有涉及,不过,大学阶段研究的切线是过函数曲线上某点且在该点与函数曲线相切的直线及其动态变化规律。本文仅说明切线和法线的位置关系,引导出切向量和法向量,借助二维平面几何来描述。 函数 g(x,y)=m(m 为常数),其图形上任意一点(x0,y0),那么,过该点与函数曲线相切的切线可由微分形式推导:g(x,y)=m⇒dg(x,y)=0,而 g(x,y)的微分是由 x 和 y 的共同变动作用引起的,再根据其偏导数为“变换因子”[6]P219,得到: 图6 切线方程 在 dg(x,y)=gxdx+gydy=0 中,将 gxdx+gydy 看作 a=(dx,dy)和 b=(gx,gy)两个向量的内积:〈a,b〉=dxgx+dygy=0,这表明 a=(dx,dy)和 b=(gx,gy)二者的位置关系是垂直的,二者方向的夹角是 90°。向量 a 指示的方向(dx,dy)是切线方向,称为切向量;向量b指示的方向(gx,gy)与切线垂直,称为法向量。由此我们可以知道,函数图像上的任何一点都有一个沿向量(gx,gy)所指的方向与此点处的切线成垂直位置关系的法线。由此我们得到一个重要结论:任何一个函数图形上的点的切线都有一个与之垂直的法线,且法线的方向可用由该函数的偏导数组成的向量来表示,它在微积分中还有一个名字,叫做梯度。 带有等式约束条件的函数极值问题,可以用二维平面几何来直观解释。目标函数f(x,y)其实是一个三维图形,即用X、Y、Z轴组成的空间立体图形。f(x,y)的等高线是在Z轴方向,沿着平行于由X轴和Y轴组成的平面“切”出来的曲线。又因为Z轴是连续的,所以“切”出来的等高线也是连续变化的。 图 7 中,f(x,y)=f0、f1、f2表示三条等高线,在同一条曲线上的 f(x,y)取得相同的值,约束曲线是 g(x,y)=m。当约束曲线 g(x,y)=m 与目标函数 f(x,y)的等高线相切时②可以简单论证:如果不相切,则总可以使等高线朝更大值或更小值的方向连续变化。,目标函数 f(x,y)才能取得极值,并且二者有一条公共的切线(图7中的虚线)。 由上边对切向量和法向量的分析可知,任意函数图形上某点的法方向就是由该函数的偏导数组成的向量所指的方向。目标函数 f(x,y)的等高线方程 f(x,y)=f1和约束曲线 g(x,y)=m 在相切点处拥有相同的切线,二者的法方向都与这条切线呈垂直关系,这也就意味着二者的法方向平行。 两个平行的法方向,从向量角度来看。在图 7 的相切处,法向量(fx,fy)和(gx,gy)的关系为:(fx,fy)=λ(gx,gy),λ①可以用任意字母表示此处的常数,只是历史文献和权威著作一直使用λ。是一个待定常数,在确定之前是变量。 图7 带有等式约束条件的函数极值 目标函数 f(x,y),在等式 g(x,y)=m 约束条件下,在极值点处满足且必定满足条件:(fx,fy)=λ(gx,gy),而这个结果可以通过人为构造的方程:Z=f(x,y)+λ(g(x,y)-m),对三个变量 x,y,λ 分别求一阶偏导为零得到。 方程(1)和(2)经过简单变形,可得到(fx,fy)=λ(gx,gy),方程(3)就是原始约束条件。解这个方程组就得到了约束条件下目标函数的极值解(x*,y*,λ*)。 通过人为构造的含有待定参数的方程来求解,再对其中的所有变量求一阶偏导并且为零,就是拉格朗日乘子法。带有等式约束条件的函数极值问题,又称作古典拉格朗日乘子法,它诞生时间较早,已经有300多年的历史[6]P157-178。300多年来,人类从未停止探索具有约束条件的目标函数极值问题,对约束条件和目标函数逐渐放松要求,并减少假设前提,由此取得了丰硕的成果,这些成果正在帮助我们解决众多经济学中的问题。现在,研究持续深入,对于经济学中看似错综复杂的现象,我们终究会找出内部规律及其生发条件,认识和理解“机械宇宙”。 现求解带有等式约束条件的函数极值问题。引入拉格朗日乘子后构造的方程,实际上是含有三个变量的新函数:Z(x,y,λ)=f(x,y)+λ(g(x,y)-m)。 三个变量(x,y,λ),其地位和作用不同。x和y是我们真正关注的,经济学中,它们经常被用作内生变量。λ是为了构建拉格朗日方程而人为“凑”出来的,起到辅助作用,它的作用类似于变分法中的扰动曲线以及动态优化中的控制变量。尽管起到辅助作用,但它并不简单,创造出来它的这种思想更是深刻并且影响深远的。当我们面临问题,找不到直接解决方案时,可以巧妙地借助一个看起来毫不相关的因素,通过它来找到解决问题的途径和方法。 事实上,两个函数 f(x,y)和 g(x,y)=m 是不同维度的,f(x,y)是三维的,而 g(x,y)=m 是二维的。更一般的情况,目标函数和约束条件函数是不同维度的,目标函数总是比约束条件函数高一个维度。在约束函数中加入辅助变量λ,其实就等于把约束函数的维度提高了一级,和目标函数的维度相同。并且,构造出来的新函数Z(x,y,λ)其实是一个具有鞍点的函数,这个鞍点就是极值解(x*,y*,λ*)。 鞍点,顾名思义,犹如一个马鞍,图像呈马鞍形状,如图8所示。只有三维图形才能可视化,二维平面不存在鞍点,因为只有一个方向的极值点。 图8 三维图形中的鞍点 三维以上图形也存在鞍点,但是无法可视化,只能借助代数形式来表达。构造出来的新函数是一个由3个自变量和1个因变量组成的系统,需要用四维才能表现出来。实际上,带有等式约束条件的目标函数极值问题,至少需要4个变量。因为目标函数至少要2个自变量,1个自变量的目标函数的约束条件只能算中学里学的函数的定义域。目标函数至少需要2个自变量和1个因变量,加上1个辅助变量λ。这就造成拉格朗日乘子法中构造的新函数 Z(x,y,λ)的极值解(x*,y*,λ*)是一个鞍点(固定不动的),但无法用几何图形直观展示出来,只能用代数形式表达: 即:对于所有的 x、y 和固定的 λ*,Z(x,y,λ*)的取值都小于等于 Z(x*,y*,λ*);对于固定的 x*、y*和所有的λ,Z(x*,y*,λ)的取值都大于等于 Z(x*,y*,λ*)。 拉格朗日乘子法在理论方面准备充分以后,其在经济学中的应用就非常简单了。在某种程度上可以说,就是用经济学的语言把数学形式重新翻译和表述一遍。拉格朗日乘子法在静态分析和比较静态分析中应用非常广泛,是基础分析工具。 党的十九大报告明确指出:“中国特色社会主义进入新时代,我国社会主要矛盾已经转化为人民日益增长的美好生活需要和不平衡不充分的发展之间的矛盾。”人民日益增长的美好生活需要就是各种有形和无形的“消费”。消费是我国经济发展的目的和根本动力。文章选取微观经济学中消费者效用最大化和消费需求领域来进行分析。 经济学中的静态分析是对市场和国民收入来说的,是指利用内生变量和外生变量构建系统模型后,求解模型中内生变量的最优解或极值解。为了更好地描述经济学中多种因素或势力互相作用、共同博弈产生的一个多方都“满意”的经济动态,把模型中各方势力均衡时的内生变量的取值称为均衡值。静态分析有两个主要特征:第一,它只关注模型的内生变量的均衡值,只关注均衡结果,不分析达到均衡的过程和状态的调整。第二,设定的模型中,所有外生变量起初都是固定不变的[7]。 以两个商品的选择为例:消费者消费数量为X和Y,为内生变量;其价格分别是PX和PY,消费者预算为M,三者都是外生变量。面临的问题是,在预算约束M条件下,使效用达到最大化。 构造拉格朗日方程:Z=U(X,Y)+λ(XPX+YPY-M),求一阶条件: 解此方程组,就可以得到均衡解(X*,Y*,λ*)。由此可见,静态分析就是求拉格朗日方程的一阶条件,然后再求解方程组。 比较静态分析就是让静态分析中的 3 个外生变量(PX,PY,M)变化起来,考察其对均衡解(X*,Y*,λ*)的影响。均衡解(X*,Y*,λ*)是从包含 3 个外生变量(PX,PY,M)的拉格朗日一阶条件方程组中解出来的,因此从函数角度看,它们组成如下关系: 并且,均衡解还满足拉格朗日方程的一阶条件。将均衡解代入一阶条件为: 对上边三个等式取全微分:允许所有变量都变化,这个变化用微分去测度,但变化的结果必须保持等式成立。而且均衡解的变化,是由三个外生变量(PX,PY,M)传导所致,因此还需要复合函数以及链式法则。 由上述三个方程组成的方程组,是构建的消费者效用最大化问题的一个系统方程:三个外生变量(PX,PY,M),两个内生变量(X*,Y*)和一个辅助变量 λ*。 要分析三个外生变量(PX,PY,M)变动对均衡值(X*,Y*,λ*)的影响,只能选择分析其中一个,而要求其他两个固定不变。例如,为了研究预算收入变化对消费者的影响,需要令PX,PY保持不变,即:dPX=0,dPY=0,将它们代入消费者比较静态系统方程组,并且3个方程两边同时除以dM(dM为收入变动且不为零),得到: 为了将上述内容表述简洁,利用矩阵表达方式重写上述方程组,可得: 最终得到了比较静态分析最简洁的表达方式。利用克莱姆法则就可以计算出dX*/dM、dY*/dM和dλ*/dM,它们可以用来测量收入的变动对消费者最优商品消费量的影响方向和程度。如果需要测量商品价格PX变动对消费者均衡值的影响,可以令M和PY保持不变,即:dM=0,dPY=0,依相同方法分析即可。 拉格朗日乘子法历史悠久,从最初的古典拉格朗日乘子法,到广义拉格朗日乘子法,再到其各种变种——欧拉-拉格朗日乘子法,乃至汉密尔顿乘子法,它至今仍是强大的分析方法。拉格朗日乘子法更是一种分析思想,与“旁敲侧击”“围点打援”“直中拒则曲中求”①借用“宁在直中取,不在曲中求”,文中意思与此句含义无关。等中国先贤智慧相通,这里面有“殊途同归”的意味。 静态分析和比较静态分析是经济学的两种研究环境:静态分析是在内生变量已知变化范围且外生变量给定不变的条件下,寻找研究领域具有重要内生变量的最优状态(均衡状态);比较静态分析是在静态分析的基础上向前延伸,在外生变量发生变化的条件下,观察均衡状态的变化情况[8]。比较静态分析较之静态分析,虽然能够测量出外生变量的变动对均衡值的影响,但是从上边的分析过程中可以看出,它也有缺点:只能分析单个而不是多个外生变量同时变化对均衡值的影响,它也不能分析动态调整过程和路径,这需要向前延伸至动态分析理论[9]。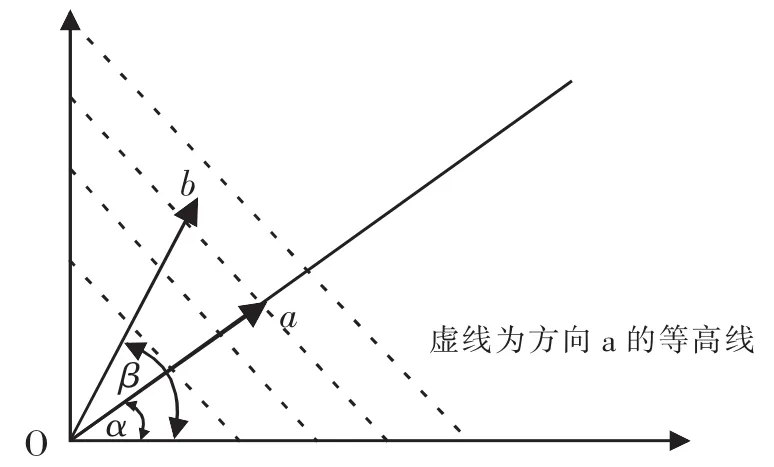
(三)带有等式约束条件的函数极值问题
三、对拉格朗日乘子法的再认识
四、拉格朗日乘子法在静态分析和比较静态分析中的应用
(一)静态分析
(二)比较静态分析
五、总结

