基于K-means++的多视图点云配准技术

梁正友，王 璐，李轩昂，杨 锋

(1.广西大学计算机与电子信息学院，广西 南宁 530004； 2.广西多媒体通信与网络技术重点实验室，广西 南宁 530004)

0 引 言

在大多数情况下，深度数据在采集过程中无法一次性获取目标对象的全貌，因此，需要一种将同一场景的2个或2个以上的点云数据叠加至同一坐标系中的技术，即点云配准技术。该技术目前已被广泛应用于假体设计、文物修复及地质勘探等领域[1-3]，可根据数据集的规模分为成对配准和多视图配准[4-5]。1992年，Besl和Mckay[6]提出的迭代最近点(Iterative Closest Point， ICP)算法是一种常见且变体最多的配准算法[7]，其基本思想是通过计算最近欧氏距离建立对应的点对关系，并迭代地调整点云间的刚性变换参数(R,T)使点云间的空间偏差最小化，从而获得配准结果。其变体例如Chetverikov等人[8]提出的裁剪ICP算法(Trimmed Iterative Closest Point， TrICP)，该方法可用于存在部分重叠的点云间的配准，但只适用于重叠率为50%以下的点集；Li等人[9]利用K-D树结构存储点云数据并用于领域搜索中，使大量的点云数据得到高效管理，从而同时提升了配准的精度和效率。然而，在数据集的视图规模较大时，将这些方法运用于成对配准，会使各视图的配准误差不断累积，且配准过程中存在初次扫描的视图和末次扫描的视图无法进行配准的问题，从而导致配准精度下降[10-11]。

多视图配准则可以减少误差积累的情况，通过依次对所有视图进行一致配准，使成对配准造成的误差均匀地分布到所有视图中[12]。受到机器学习的启发，研究者将深度学习方法引入多视图配准技术中。Chang等人[13]提出采用2个连续卷积神经网络(Convolutional Neural Networks， CNN)模型估计点云间的刚性变换，改进了配准技术中存在的耗时问题；Kurobe等人[14]提出了基于CorsNet连接局部及全局特征集成更多的信息用于回归点云的对应关系，从而得到准确且高效的结果。

聚类算法作为无监督学习中常见的分类算法[15]，在配准问题中取得了较好的效果。Zhou等人[16]提出了一种利用K-means算法最小化积分误差和优化融合点位置的方法，将邻近视图重叠部分的数据进行双向移动，但该方法并未涉及点云间刚性变换的更新；Evangelidis等人[17]提出了一种基于聚类的联合配准方法，使用批处理和增量期望最大化方法估计高斯混合模型的参数和最优集合用以配准，但该方法的鲁棒性和精度有限；Ji等人[18]通过修正加权平均法向量节点，并利用均值漂移聚类算法得到局部最大值模型，其配准速度较快，但准确率有限；Zhu等人[19]利用K-means算法对多视图进行配准，能够提升多视图点集的配准效率。

本文针对多视图点集中可能存在噪声、离群点及遮挡等影响点云配准结果的问题，提出一种基于K-means++[20]的多视图点云配准算法。首先，利用K-means++算法的随机播种技术[21]对各视图点集求取质心并进行聚类，然后根据K-D树的最近邻近点算法(K-NearestNeighbor， KNN)[22]建立各视图的对应点集，最后根据各视图聚类结果对整体点云进行成对配准，依照扫描次序运用ICP算法求取点集间的刚性变换矩阵，从而得到配准结果。在Stanford三维点云数据集中的实验结果表明，本文提出的方法在配准精度上优于其他方法，且对添加噪声、存在数据缺失的点集具有鲁棒性。

1 本文方法

1.1 基于K-means++的点云聚类

K-means++算法作为一种高效聚类算法，已广泛应用于各个领域，其基本思想是：首先，从数据集中随机选取一个点作为初始质心；其次，通过随机播种技术选取其他的质心，并认为与当前已存在的质心距离最远的点，具有更高的概率成为新的质心；最后迭代地对数据集进行分簇与质心的更新，直至达到收敛条件则停止。

对于多视图点集，本文先对每个视图进行下采样，并给定初始的刚性变换，则基于K-means++的点云聚类算法过程描述如下：

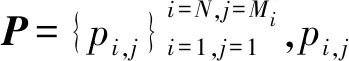
p′i,j=Ri×pi,j+ti

(1)

Step3根据随机播种技术，将与已有质心点最远的点作为新的质心，即通过重复遍历点集P′中的每个点，并根据公式(2)，分别计算其与目前质心的欧氏距离，从而选取出初始的质心集合。

(2)

其中，a为当前已有的质心个数。

(3)

Step5更新质心，公式如下：

(4)

Step6计算质心集合的位移差值，若其小于设定阈值或达到预定最大迭代次数时，得到最终的聚类结果，否则回到Step4。

1.2 基于K-means++的多视图点云配准

在近几年的研究中，已有学者将聚类算法用于多视图配准。本文将多视图配准问题看作是一种扩展的聚类问题，即假设所有参与的配准点集均由聚类后的点云数据提取，其质心能够组成一个精确的模型。因此，本文将基于K-means++的点云聚类应用于多视图配准中，通过K-means++算法从各视图的点云数据中提取质心，从而得到配准算法所需的点集。

(5)

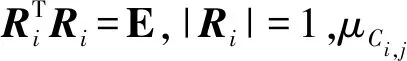
算法1 基于K-means++聚类的多视图点云配准

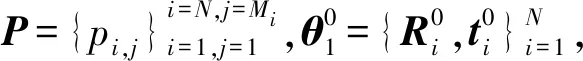
Begin:

1 对P添加初始的刚性变换，得到多视图点集P′;

2q=0;

Repeat:

3.1h=0;q=q+1;

3.2 Repeat:

3.2.1h=h+1;

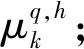
3.2.4 计算质心的位移差值E;

UntilE达到收敛条件或h>H;

3.3 fori=2:N

3.3.1 根据ICP算法计算各聚类点云与点集间的刚性变换矩阵;

3.3.2 对多视图点集进行刚性变换;

End

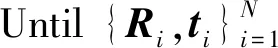
End

由算法1分析可得本文方法的每次迭代中不同操作的时间复杂度：设M为N个视图的总点云数量，K为聚类质心的数量，则建立K-D树的时间复杂度为O(KlogK),点集分簇的时间复杂度为O(MlogK)，更新聚类中心和计算刚性变换的时间复杂度都为O(M)。

2 实验与结果分析

2.1 实验建立与评价指标

本文的数据集采用Stanford三维点云数据集中的模型，分别是Bunny、Armadillo、Buddha和Dragon，各模型如图1所示。其中，Bunny模型包括10个视图，共362272个点；Armadillo模型包括12个视图，共307652个点；Buddha模型包括15个视图，共1099005个点；Dragon模型包括15个视图，共469193个点。这些模型的各个视图存在一定数量的离群点以及由遮挡造成的数据缺失。以Armadillo模型为例的多视图点集可视化结果如图2所示。

图1 点云模型

图2 Armadillo模型的多视图点集可视化

为了验证所提出方法的配准结果，实验环境为Windows 10(64位)操作系统、Intel(R)Core(TM)i5-8250U CPU@1.60 GHz计算机，代码在Matlab 2018b上实现。为了消除实验过程中的随机性，分别对各方法进行了50次蒙特卡洛实验，并取其旋转误差ER和平移误差Et×10-3m的均值。设多视图点集添加的随机真实值为(Ri,g,ti,g)，通过配准算法得到的刚性变换矩阵为(Ri,w,ti,w)，则通过Forbenius范数计算旋转误差ER，度量公式表示为：

(6)

平移误差Et×10-3m的度量公式表示为：

(7)

2.2 对比试验与结果分析

为充分描述本文方法的性能，采用4种配准算法与其进行对比，包括：基于ICP的多视图配准算法、基于TrICP的多视图配准方法[19]、基于K-means的多视图配准方法[24]和基于遗传算法(Genetic Algorithm, GA)的多视图点云配准方法(GA-TrICP)[25]。在实验中，将点云聚类的平均点数设置为num=25，设X为总点云数，则质心的数量K=X/num。

2.2.1 多视图点集配准精度

图3和图4分别描述了不同算法在4个多视图点集进行实验的随机配准结果的横截面图和整体模型的可视化结果，表1为详细的配准精度。可以看出：为多视图点集分别添加随机的空间变换后，基于ICP的多视图配准算法的平移误差较大，这是由于ICP算法本身易于陷入局部最优解，往往不能获得良好的配准结果；基于TrICP的多视图配准算法的配准结果与本文相比略差，在Dargon和Buddha模型的配准中平移误差较大，无法获得较好的效果；基于K-means的多视图配准方法和基于GA算法的多视图点云配准方法在部分模型上配准效果欠佳，且基于GA算法的多视图点云配准方法需要大量的参数设置。综上所述，本文方法利用K-means++算法将多视图配准问题看作一个拓展的聚类问题，对多视图点集进行聚类，并利用质心组成的模型对各视图交替地计算其对应的刚性变换矩阵，在各个模型的配准中都能够获得满足配准需求的结果，且具备较好的配准精度。

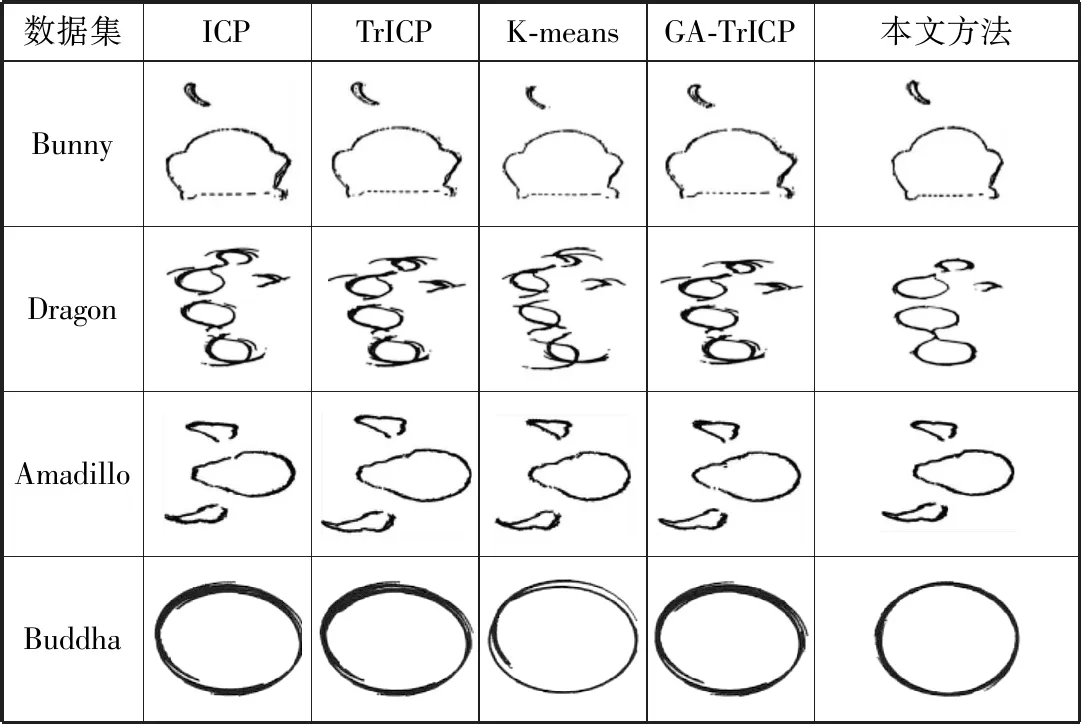
图3 不同算法在多视图点集的配准结果横截面

图4 不同算法在多视图点集的配准结果

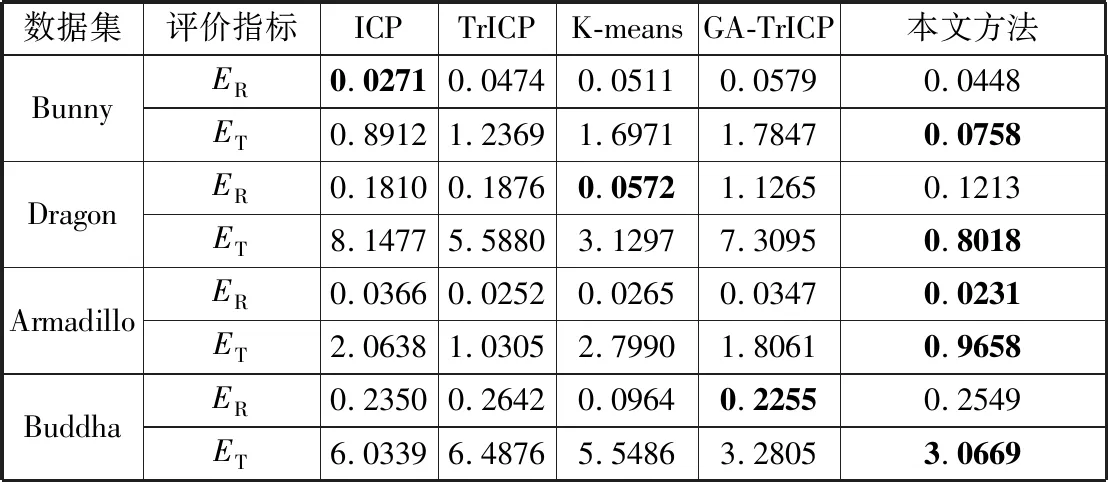
表1 不同算法在多视图点集的配准精度的比较

2.2.2 多视图点集配准鲁棒性

为了更好地描述本文方法的鲁棒性，表2、表3、表4分别为不同算法在分别添加[-0.01f,0.01f]、[-0.02f,0.02f]和[-0.03f,0.03f]的高斯噪声后得到的配准结果。从表中可以看出：在添加高斯噪声后，相比基于TrICP算法、K-means算法和GA-TrICP算法的多视图配准算法，本文方法依然能够达到较好的精度。综上所述，本文方法结合K-means++算法应用于多视图配准，在添加随机的初始空间变换及噪声的多视图数据集中，均能取得较好的配准结果，与其他同类算法比较，本文为多视图配准技术提供了一种更具鲁棒性的方法。

表2 不同算法在添加[-0.01f,0.01f]高斯噪声后，点集的配准精度的比较

表3 不同算法在添加[-0.02f,0.02f]高斯噪声后，点集的配准精度的比较

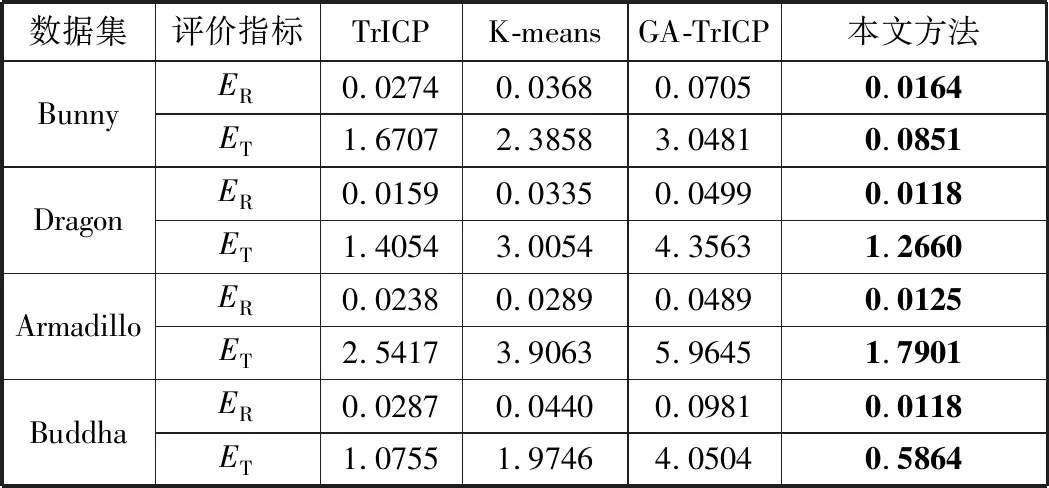
表4 不同算法在添加[-0.03f,0.03f]高斯噪声后，点集的配准精度的比较

3 结束语

对存在噪声、离群点的大规模点集进行配准具有挑战性，本文针对这一问题提出了一种基于K-means++的多视图点云配准方法。通过K-means++算法对各视图点云数据有效地提取质心，并根据其基本思想对点云完成聚类，其次利用K-D树结构存储大规模数据，从而提升对应点集的搜索效率，最后按照扫描顺序将各视图聚类后的点云数据作为源点集，再采用成对配准的方法计算源点集与其他视图间的刚性变换参数，从而获得更好的配准结果。本文方法在Stanford三维点云数据集上的实验结果表明，其配准结果的精度和鲁棒性优于近年提出的多视图配准算法。