一种HRG模型初始化算法及在链路预测中的应用
祝丁恺,铁治欣,2,洪顺贺
(1.浙江理工大学信息学院,浙江 杭州 310018; 2.浙江理工大学科技与艺术学院,浙江 绍兴 312369)
0 引 言
现实世界中的很多复杂系统可以抽象成复杂网络模型进行分析研究,在对这些复杂网络研究过程中,数据的缺失和不准确是无法避免的。如何利用现有的数据来挖掘缺失的信息以及错误的数据是当下需要解决的问题。近年来,链路预测被广泛关注[1]。链路预测可以是预测复杂网络中当前不相连的节点之间连接的可能性,也可以是预测复杂网络中确实存在的连边但尚未被探测到,亦或是预测当前复杂网络存在的连边中哪些是错误的连边[2]。链路预测不仅在好友推荐、标签分类等实际场景中有着丰富的应用,而且对网络的结构与演化[3-5]以及网络中节点的相似性[6]刻画起着重要的推动作用。
在链路预测的研究中,网络的层次结构是一个较少受到关注的点。现实世界中的网络通常具有一定的层次组织形式。层次随机图(HRG)作为一种可以从网络数据中推断出层次结构的模型,不仅可以用于网络中社团的挖掘,还可用来预测网络中缺失的链接。Clauset等人[7]利用数学上的统计推断工具(极大似然法[8]和蒙特卡洛抽样算法[9-10])将层次随机图模型与观测的网络数据进行拟合来对网络中的缺失链路进行预测。该方法不仅具有较高的预测准确度,而且与现有的一些链路预测算法相比,更适用于一般的网络结构。
近年来,层次随机图模型在链路预测中的应用被广泛关注。为了提高层次随机图模型在二分网络当中的预测精度,2011年,Chua等人[11]提出了适合二分网络的层次随机图模型(BHRG)。同年,Allen等人[12]提出了适用于加权网络的层次随机图模型(wHRG),同时针对那些边具有多重属性的加权网络,他们又进一步提出了基于多重属性加权网络的层次随机图模型(vHRG)。2016年,田甜等人[13]将层次随机图模型应用到脑网络的链路预测中,实验也达到了较为理想的效果。然而,利用该模型进行链路预测时具有较高的时间复杂度,这就导致现阶段该模型只能适用于小规模网络的链路预测,这大大限制了该模型的适用范围。因此,寻找一种既能减少时间开销又能准确反应网络的真实结构的方案已迫在眉睫。
本文深入研究基于层次随机图模型的链路预测过程,针对层次随机图模型的初始化阶段,提出一种新的层次随机图初始化方案。该方案主要分为2个步骤:1)为网络中的边排序,本文引入节点相似性指标(LHN-I指标),利用该指标对网络中的边进行排序;2)构造层次随机图模型,本文设计一种将网络中的顶点插入到层次随机图模型中的规则,当将排序好的边的顶点放入层次随机图模型中时,该规则能够保证顶点在层次随机图模型中的唯一性。基于该方案构造出的层次随机图模型相较于现有的方案具有更佳的表现。
1 层次随机图模型与链路预测
1.1 HRG模型的基本概念
设真实网络是一个具有n个顶点的简单无向图G,层次随机图可以看作是一种树形图D(本质是一个二叉树),它由内部节点、内部边以及叶子节点构成。其中,G中的n个顶点对应于D中的n片叶子节点。任意2片叶子节点i、j之间由D的n-1个内部节点中的某一个r联系起来,此内部节点r也称为i和j的最低共同祖先。内部节点与内部节点之间由一条内部边相连,共有n-2条这样的内部边。每个内部节点r会被赋予一个概率值pr,并且规定任意2个叶子节点i、j的连接概率pij就等于它们的最低公共祖先所对应的概率值p即pij=pr。那么,由树形图D和概率值pr的集合(D,{pr})定义了一个层次随机图。图1展示了一个含有7个顶点的简单无向网络及其对应的某个层次随机图模型。

图1 一个简单无向网络和其对应的某个层次随机图模型
1.2 层次随机图与网络的拟合

(1)
其中,Lr、Rr表示以r为内部节点的左子树和右子树的叶子节点个数;Er表示以r为内部节点的左子树的叶子节点与右子树的叶子节点之间反映在网络中的真实连边数。似然值越高说明该层次随机图与给定的网络G拟合得越好。对于一个确定的层次随机图,利用极大似然法得出pr的最大似然估计值为:
(2)
那么,引入此最大似然估计值的树形图的似然为:
(3)
1.2.1 MCMC算法
为了寻找最适合观察网络的一个或多个层次随机图模型,使用遍历比较的方法计算量极其庞大。为此,使用马尔科夫链蒙特卡洛(MCMC)算法层次随机图空间集合进行抽样,使得每个层次随机图抽取的频次正比于该层次随机图的最大似然值。MCMC算法的步骤为:
Step1随机构造一个初始层次随机图来初始化马尔科夫链。
Step2构造马尔科夫链,随机选择层次随机图中的一个内部节点r,利用子树重排技术改变该内部节点的子树位置以产生一个新的层次随机图D′。
Step3运行蒙特卡洛方法[9]直至平衡,每当马尔科夫链上产生新的层次随机图D′后,需利用Metropolis-Hastings(M-H)标准[15]来接受或者拒绝它。如果L(D′)-L(D)≥0,则接受D→D′的转换,否则以概率L(D′)/L(D)判断是否接受D′作为当前树形图,如果不接受这种转换,树形图保持原样。M-H标准能够确保马尔科夫链收敛平衡。
Step4当马尔科夫链趋于平稳后,每隔一定的时间采样一次,得到最佳层次随机图样本。
1.2.2 子树重排
为了能够运行MCMC算法,需要找到一种能够将树形图集合中的每个元素联系起来的方法。简单来说,为了构造一条马尔科夫链,需要通过某种技术能够将当前形态的树形图转换成另一种形态,这就是子树重排技术。对于一个给定的树形图,它的任意一个内部节点(非根节点)都由3部分组成:左子树、右子树以及兄弟子树。而子树重排技术就是对某个选定的内部节点的子树位置进行重新排列,如图2所示。

图2 子树重排
对于一个选定的内部节点,有2种方法可以重新排序这些子树。以图2(a)为例,假设粗框标记的内部节点r为当前被随机选中的内部节点,该内部节点的左子树为a,右子树为b,兄弟子树为c。从此状态出发,通过对选中的内部节点的子树之间的位置进行交换可以产生图2(b)与图2(c)这2种状态。事实上,这3种状态可以相互转换。
1.3 基于HRG模型的链路预测算法
使用层次随机图模型进行链路预测的算法如下:
Step1导入网络数据,构造初始层次随机图并初始化马尔科夫链。首先读取网络中数据,为层次随机图分配合适的内存空间,通过选择一个随机的初始树形图初始化马尔科夫链。
Step2运行MCMC算法直至平衡。从初始树形图D出发,在马尔科夫链上的每一步都包括:1)随机选取一个内部节点,在对其子树重排所产生的2种形态中随机选择一种以生成一个新的树形图D′;2)根据Metropolis-Hastings标准接受或拒绝新产生的树形图。
Step3抽样。当马尔科夫链平衡时,从马尔科夫链生成的树形图中每隔一定时间抽样一次(可手动设置抽样次数)。
Step4链路预测并排序。对于还没有已知连接的每对顶点(i,j),计算它在每个被抽样的树形图中的连接概率pij,然后求得pij的平均值。按照pij的大小进行从大到小排序,排在前面的说明连接的可能性越大。
Step5计算AUC[16]。利用AUC指标对预测的结果进行分析,最终得出AUC值的大小,AUC值越高,说明算法的预测精度越好,当AUC值>0.5时,说明算法要比随机方法更好。
2 一种层次随机图模型初始化算法
在1.3节中介绍的利用层次随机图进行链路预测的算法中,步骤2的花费时间在整个算法花费时间中占据着较多的分量,也就是说从初始层次随机图迭代到收敛后的层次随机图需要花费大量的时间。通过研究发现,利用现有的方法构造出的初始层次随机图的似然值往往与收敛后的层次随机图的似然值相差甚远。在小规模的网络当中,这种随机的构造方法能够花费较短的时间从初始似然值过渡到最优似然值,然而,随着网络规模的增大,从初始状态到最优状态所花费的迭代次数将呈指数上升。因此,为了减少从初始层次随机图到最优层次随机图之间的迭代次数,本文提出一种层次随机图模型的初始化方法。
2.1 算法介绍
层次随机图模型是一种层级结构,对于该模型的初始化,本文采用一种自下而上的构造方法。其核心思想为:按序提取网络中每条边的2个顶点,将这2个顶点作为树形图的叶子节点并有选择地使用内部节点与它们关联。在这之中涉及3个关键技术点:1)如何按序提取网络中的边,也就是说,使用什么准则给网络中的所有边进行排序;2)如何判断当前边的2个顶点是否重复,也就是说,应该避免相同的顶点重复出现在树形图之中;3)该采用何种策略将被提取的边的2个顶点放入到树形图的叶子节点当中去。
对于第一个技术点,本文引入了相似性指标的概念,利用相似性指标作为权重的计算方法,为网络中的所有边按照权重的得分从大到小进行排序。对于第二个技术点,本文采用红黑树这一数据结构,每当提取边的2个顶点时,判断这2个顶点是否在红黑树当中,并且将不在红黑树中的顶点插入到红黑树当中。这样,每次提取边的顶点的过程中就可以判断顶点是否重复出现。由于红黑树的查找、插入的时间复杂度为O(logn),所以花费的时间较少。对于第三个技术点,本文总结了将边的顶点插入到叶子节点的过程中遇到的所有情况,并对各自的情况给出了详细的解决方案。设每条边的头顶点和尾顶点分别为Vx,Vy,顶点Vi对应于层次随机图中的叶子节点为leafi,叶子节点leafi的最远祖先节点为maxAncestori,顶点Vi的度称为ki,被访问过的顶点集合为{Vi},那么将边的顶点插入到叶子节点的过程中遇到的各个情况以及对应的解决方案如下:
1)Vx∉{Vi}且Vy∉{Vi} 。
将Vx、Vy放入集合{Vi}中并生成叶子节点leafx和leafy,用一个内部节点连接leafx和leafy。
2)Vx∉{Vi}且Vy∈{Vi} 。
将Vx放入集合{Vi}中并生成叶子节点leafx,考虑如下情况:①如果kx>ky,那么首先找到maxAncestory,将maxAncestory与leafx用一个内部节点进行连接;2)如果kx≤ky且leafy是其父节点的左孩子,那么首先用一个内部节点连接leafx与leafy的父节点的右孩子,其次将leafy的父节点的右孩子替换成此内部节点;③如果kx≤ky且leafy是其父节点的右孩子,那么首先用一个内部节点连接leafx与leafy的父节点的左孩子,其次将leafy的父节点的左孩子替换成此内部节点。
3)Vx∈{Vi}且Vy∉{Vi} 。
将Vy放入集合{Vi}中并生成叶子节点leafy,考虑如下情况:①如果kx 4)Vx∈{Vi}且Vy∈{Vi} 。 若maxAncestorx与maxAncestory不是同一个,那么将leafx和maxAncestory用一个内部节点进行连接,否则不进行任何操作。 结合上述3个技术点的解决方案,整个层次随机图模型的初始化算法如下: 1)计算网络中每条边的权重得分; 2)将网络中边的权重值按照从大到小进行排序; 3)选取当前权重最大的那条边,判断该边的2个顶点是否已出现在树形图中,并按照上述策略将需要被操作的顶点插入到层次随机图当中; 4)重复步骤3,直至所有边都提取完毕; 5)为每个内部节点计算pr。 在2.1节中提到,为了初始化树形图,本文引入了相似性指标的概念,然而相似性指标众多,不同的相似性指标对于初始层次随机图的构造会产生不同的影响。因此,为了探究采用哪个指标构造出的初始树形图的似然值更高,本文采用了6种不同的相似性指标并构造出了6种不同的初始层次随机图,这6种指标如表1所示。 表1 相似性指标 2.3.1 数据集与实验环境 为了探究融入了哪一种指标所构造出的层次随机图模型似然值最高。本文分别使用FWFB、C.elegans和Metabolic这3个真实网络进行实验。实验中所有被使用到的网络都进行了无向化处理。表2展示了3个网络的信息。 表2 数据集 FWFB是佛罗里达海湾雨季的食物链网络[21],其中每个顶点代表一种生物,每条边代表生物之间的捕食关系。该网络存在31条具有互惠关系的边,在实验过程中,这些互惠边会被忽略。 C.elegans是线虫的神经元网络[22],其中每个顶点代表线虫的神经元,每条边代表神经元突触或者间隙连接。该网络是有向网络,在实验过程中会忽略边的有向性。 Metabolic是线虫的代谢网络[23],其中每个顶点代表代谢物(如蛋白质),每条边代表代谢物之间的相互作用。在该网络中,由于某些代谢物可以自我迭代,因此存在一些自循环的边,在实验的过程中这些自循环的边会被主动剔除。 所有实验都是在基于4 GB内存的Linux内核和英特尔酷睿i3-2100 CPU的Deepin操作系统平台上进行的。 2.3.2 实验分析 在对树形图求对数似然的时候,其值通常为负数,为了方便在图表中观察似然值的结果,本实验对其取相反数,因此似然值的相反数的值越小,说明初始HRG模型构造得越理想。 图3展示了基于不同相似性指标的HRG模型的构造算法在3种真实网络下的表现情况。其中横坐标表示网络的类型,纵坐标表示在特定网络下,利用不同的相似性指标所构造出的初始树形图的似然值的大小。从图中可以明显发现,融入了相似性指标的初始HRG模型构造方法比随机构造初始HRG模型有着更好的初始似然值。在这些相似性指标当中,基于LHN-I指标构造出来的HRG模型有着更好的初始似然值。 图3 不同指标在3个网络中的表现 将原始构造方法与基于LHN-I指标的构造方法单独做对比,如图4所示,在初始HRG模型似然值的结果上,基于LHN-I指标的构造方法比原始构造方法在FWFB网络、C.elegans网络、Metabolic网络中分别提升了25%、18%、42%左右。 图4 基于LHN-I指标构造的初始HRG模型 因此,基于LHN-I的HRG模型构造方法在一定程度上提高了初始HRG模型的质量。 在1.3节中介绍的利用层次随机图进行链路预测的步骤中,现有的方法是采用随机构造初始层次随机图的方式来初始化马尔科夫链,为了探究提高初始层次随机图的质量能否提升MCMC算法的收敛速度,利用上述的3个网络进行了3次实验。对于每次实验,分别使用随机算法构造初始层次随机图和使用初始化算法构造初始层次随机图的方式来初始化马尔科夫链,之后各自运行MCMC算法。 在FWFB网络中,如图5所示,若采用层次随机图初始化算法构造出来的层次随机图模型来初始化马尔科夫链,MCMC算法大约经过了2 min逐渐趋于稳定;而若使用随机构造出来的层次随机图来初始化马尔科夫链,那么MCMC算法则需要大约8 min才逐渐趋于稳定。因此,在使用了初始化算法的情况下,MCMC算法收敛所需的时间相较于随机的方法大约提升了75%。 图5 在FWFB网络中2种算法的实验对比 如图6所示,在C.elegans网络中,若采用层次随机图初始化算法构造出来的层次随机图模型来初始化马尔科夫链,MCMC算法收敛速度相对较快,大约经过了0.5 min,MCMC算法逐渐趋于稳定;而若使用随机构造出来的层次随机图来初始化马尔科夫链,那么MCMC算法则需要3 min左右的时间才逐渐趋于稳定。因此,在使用了初始化算法的情况下,MCMC算法收敛所需的时间相较于随机的方法大约提升了83%。 图6 在C.elegans网络中2种算法的实验对比 如图7所示,在Metabolic网络中,若采用层次随机图初始化算法构造出来的层次随机图模型来初始化马尔科夫链,MCMC算法大约经过了3 min逐渐趋于稳定;而若使用随机构造出来的层次随机图来初始化马尔科夫链,那么MCMC算法则需要大约6 min才逐渐趋于稳定。因此,在使用了初始化算法的情况下,MCMC算法收敛所需的时间相较于随机的方法大约提升了50%。 图7 在Metabolic网络中2种算法的实验对比 结合新提出的HRG模型初始化方法,本文提出一种改进的基于层次随机图模型的链路预测算法(N-HRG)。N-HRG链路预测算法的流程如下: Step1导入网络数据,利用提出的HRG模型初始化方法构造一个优化的初始层次随机图来初始化马尔科夫链; Step2运行MCMC算法,直至马尔科夫链平衡; Step3抽样; Step4链路预测并排序; Step5计算AUC[16]。 为了探究本算法的预测性能,依然使用2.3节中的3个网络实例(FWFB网络、Metabolic网络以及Celegans网络)并将给定的网络中的边的集合分成2部分,一部分作为训练集,另一部分作为测试集。训练集是作为链路预测算法的输入,而测试集是用来与链路预测算法的输出进行比较。在划分数据集的过程中,需要确保训练集中的边具有连通性,即不存在孤立的节点。数据集将按照5种不同的比例进行划分,比例分别为10%和90%、20%和80%、30%和70%、40%和60%、50%和50%,前者为测试集所占的比例,后者为训练集所占的比例。 本次测试的这3种网络的运行环境为:基于Linux内核的Deepin操作系统,运行内存为4 GB,CPU采用Inter Core i3-2100 3.1 GHz。 本文使用AUC指标作为衡量链路预测精度的标准,AUC是指ROC曲线(Receiver Operating Characteristic Curve)下的面积[24]。按照定义,需要首先画出ROC曲线,然后计算出ROC曲线所覆盖的面积,最终得到AUC的值。事实上,对于样本很多的情况,一般采用抽样比较的方式得到一个近似的AUC而不需要绘制出ROC曲线。利用抽样比较的方式,AUC可以被定义为: (4) 其中,n代表独立实验的总次数,n′代表n次实验当中测试集中的边的得分值大于不存在的边的得分值的次数,n″代表测试集中的边的得分值等于不存在的边的得分值的次数。也就是说,独立进行n次实验,在每次实验中,从测试集中和不存在的边中各随机抽取一条边,比较两者的得分值。如果测试集中的边的得分值大于不存在的边的得分值,那么加1分,如果测试集中的边的得分值等于不存在的边的得分值,那么加0.5分。 从式(4)可以看出,如果测试集中的边的得分与不存在的边的得分是随机产出的,那么AUC的值近似为0.5。因此,如果一个链路预测算法的AUC>0.5,那么就说明该链路预测算法要比随机的方法更好。 将本文方法与其他一些基于相似性指标(Salton指标[19]、Jaccard指标[18]、CN指标[17]以及ACT指标[25])的链路预测算法进行比较,将训练网络的密度作为输入,输出为各个算法在对应训练网络密度下的AUC大小。在实验过程中,AUC值越高,预测精度越高。 在FWFB网络中,如图8所示,N-HRG方法在5个不同的训练网络密度中的预测精度始终明显高于其他方法,并且即使网络数据在丢失了50%的情况下,N-HRG方法的AUC值还能保持在0.8附近,这意味着在网络丢失一半细节的情况下,N-HRG方法还能保持较高的预测精度。值得注意的是,当训练集的密度为50%时,基于Salton指标的链路预测算法的AUC值反而低于0.5,这说明其预测精度要比随机方法的差。 图8 不同链路预测算法在FWFB网络中的对比 如图9所示,在C.elegans网络中,在不同的训练集密度的测试下,这5种方法的预测精度都要比随机方法的好。其中,除了基于ACT指标的链路预测算法,其他算法的预测精度都随着训练集密度的增加而增加,并且N-HRG算法在5个不同的训练网络密度中的预测精度始终高于其他算法。当训练集密度在80%和90%时,基于CN指标的链路预测算法的预测精度与N-HRG算法的差距较小。当训练集密度在50%时,N-HRG算法依然能保持着较高的预测精度,而其他算法只能得到较低的预测精度。 图9 不同链路预测算法在C.elegans网络中的对比 如图10所示,在Metabolic网络中,N-HRG算法在5个不同的训练集密度中的预测精度始终高于基于Salton指标、Jaccard指标以及ACT指标的链路预测算法。在训练网络的密度为50%和60%时,N-HRG算法的预测精度还优于基于CN指标的链路预测算法的预测精度。但当训练网络的密度大于80%时,基于CN指标的链路预测算法的预测精度略微高于N-HRG算法的预测精度。值得注意的是,当训练集密度在50%时,N-HRG算法的AUC值依然保持在0.8以上,而其他方法都位于0.8以下。 图10 不同链路预测算法在Metabolic网络中的对比 从整体来看,N-HRG算法的预测性能在实验中有着较好的表现,并且当网络缺失大量细节的情况下,依然能保持较好的预测精度,这对一些实际应用有着较大的帮助。除此之外,N-HRG方法在一些特定的网络下(如食物链网络)的预测性能有着巨大的优势。 为了解决层次随机图模型在初始化阶段效率不高的问题,本文提出了一种新的层次随机图模型初始化方法。在层次随机图的初始化阶段,引入LHN-I指标为网络中的边排序,并且设计了一种将网络顶点插入到模型中的方法,使得构造出的层次随机图模型具有较高的似然,这就间接减少了MCMC算法的迭代次数,进而降低了链路预测的时间消耗,提高了对更大规模网络进行链路预测的可行性。除此之外,通过对3个真实网络的链路预测实验,结果表明基于N-HRG的链路预测算法相比于基于节点相似性的链路预测算法有着更好的预测精度。2.2 指标的选择

2.3 实验分析

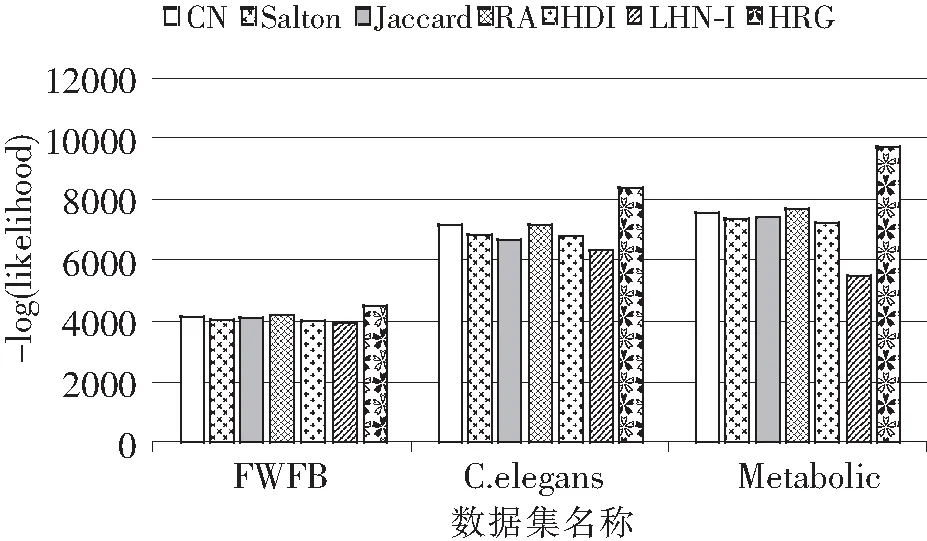




3 链路预测实验与分析
3.1 N-HRG链路预测算法的步骤
3.2 数据集的划分与实验环境
3.3 评价指标
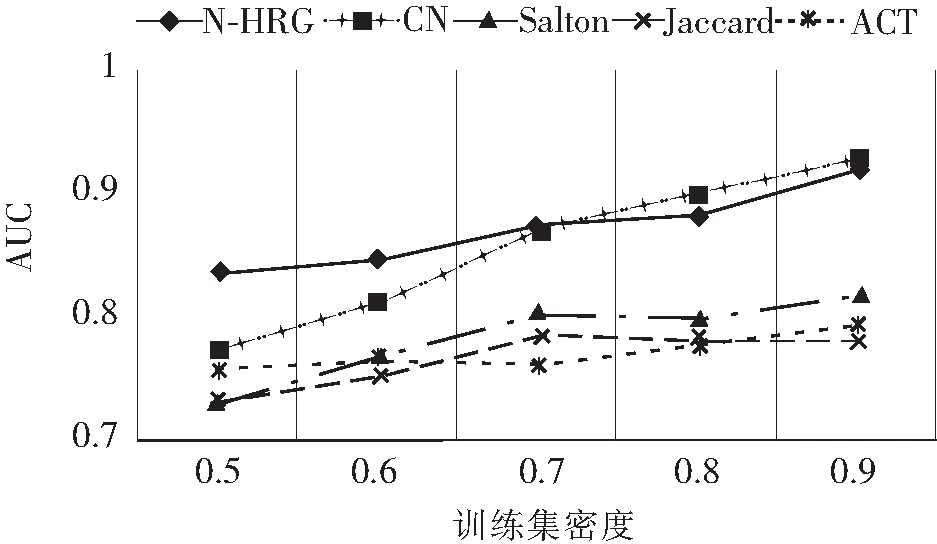
3.4 实验分析


4 结束语

