基于长短期记忆网络修正测距的水下定位算法

纪 平,郭 瑛

(青岛科技大学信息科学技术学院,山东 青岛 266100)

0 引 言

水下无线传感器网络(Underwater Wireless Sensor Networks， UWSNs)是目前人类探索、监测、开发海洋的主要手段。最近几年，水下无线传感器网络的发展稳中向好，由于各种基于海洋的产业正在蓬勃发展，社会的关注也逐渐聚焦于探索海洋、开发海洋和保护海洋[1]。水下无线传感器网络一直为海洋环境监测、自然灾害防御和军事防御等许多应用领域提供了充分的技术支持[2]。传感器节点收集到的数据需要准确的位置信息才能发挥应用的价值，而因为北斗、GPS等卫星定位使用的信号不能在海洋环境中传播，陆地上的定位算法又不能够适应海洋环境中的复杂性和多变性，水下定位算法迅速成为了研究热点，引起了学术界的广泛关注[3]。

在水下定位研究方向中，定位准确性一直是这个研究方向的难题[4]，由于水下环境特殊而又复杂，水下传感器节点的位置会随着水流的波动、潮汐的影响产生位置变化，水下节点本身续航问题，以及海水污染等环境因素造成水声信号传播不稳定等诸多因素都会造成定位不准确、定位有偏差等问题，所以水下定位算法成为水下无线传感器网络的关键技术之一[5]。虽然水下定位的困难不仅仅是上述几个，但是这些问题足以证明水下定位所面临的重重困难，而使得水下节点定位变得非常具有挑战性[6]。

目前，水下定位算法主要分为基于测距和基于估计2种[7]。其中基于测距的水下定位算法定位精度高且算法发挥稳定，所以大多数水下定位算法都是基于测距的。而基于测距的定位算法需要测量信标节点与未知节点之间的距离来计算未知节点的坐标，但是由于水声信号传播速率深受海洋环境因素的影响，导致利用其测距时往往出现测距误差，致使定位效果不理想。

本文针对上述问题提出一种基于长短期记忆网络(Long Short-Term Memory， LSTM)修正测距的水下定位算法，通过深度学习领域中的LSTM网络结合基于信号到达时间差测距算法(Time Difference Of Arrival， TDOA)使得本文改进的多边定位算法更加精确，不仅克服了上述问题，而且有效地提高了算法的定位精度。其中LSTM能够充分发掘海洋环境历史数据的时序性特征，拟合出海洋对比水声信号传播速率的影响规律，从而能够预测出利用水声信号传播的TDOA计算出的测距值的修正值。本文利用LSTM修正TDOA测距值是对TDOA测距修正的全新尝试，并取得可观的修正效果。最后利用本文改进的多边定位算法对测距修正值实现对未知节点的精准定位。

1 相关工作

水下传感器网络中有2种类型的节点：信标节点和传感器节点[8]。信标节点是位置坐标已知的节点，用于定位传感器节点，也称为锚节点。传感器节点用于监视环境或跟踪海洋生物和其他传感信息，因此需要对其进行定位，它们的计算能力、存储容量、通信范围和电池电量受到限制。

在UWSN的定位过程中，未知节点将信标节点作为位置参考，信标节点不能使用GPS或其他在水下环境传播期间使用电磁信号的定位系统来更新其位置信息[9]，这将更容易影响整个水下传感器网络的定位精度。根据是否需要测量距离、对锚节点的要求或同步机制等不同要求，水下传感器网络定位算法有许多分类，本文根据以上分类标准介绍一些代表性的定位算法。

根据邻居节点之间相互通信时需不需要测量节点之间的距离和角度等承载信息，可以将定位算法分为基于测距的定位算法和基于估计的定位算法[10]。基于测距的方法通过各种算法估计距离，然后将它们转换为位置信息。基于估计的方法不需要距离测量和承载信息，但使用局部拓扑和相邻信标的位置来获得位置估计。然而，基于估计的方案只能获得一个粗略的位置，准确性很低。

文献[11]提出了ALS算法，它是一种有效的区域定位算法。该方案估计传感器在特定区域内的位置。信标节点将信标信号广播到传感器节点并发送具有变化的功率电平的声信号。传感器节点被动地监视信号并记录接收的信息，然后将其转发到接收器。接收器使用从传感器节点收集的信息来估计传感器所在的区域。

根据算法对锚节点的要求，可以将定位算法分为基于锚的算法和无锚算法[12]。使用锚节点在UWSNs的定位算法中是比较常见的。然而，锚节点不是必需的，并且一些学者已经提出了不需要锚节点的自定位算法[10]。

文献[13]提出的HLS算法是典型基于锚的方案。该方案由4种类型的节点组成：表面浮标、可拆卸升降收发器、锚节点和普通节点。此外，该方案将节点分为2个阶段：首先，锚节点使用基于范围的分布式方法来定位自身；其次，普通节点使用区域定位方案来实现无位置集中式算法。文献[14]提出的AFLA算法是一种用于主动受限UWSNs的无锚定位算法。该算法使用相邻节点之间的关系来开启定位计算。水下传感器节点在海中漂浮并在半球形区域内移动，具有未知位置的节点广播消息并同时从其他节点接收信息，当节点从2个不同节点接收到2条消息时，它将启动位置计算过程。

根据算法中节点之间的通信特性，将UWSNs定位算法分为2类：单级算法和多级算法[15]。单级算法意味着所有传感器节点和参考节点之间的消息交换是直截了当的。获得位置后，它们仍然是被动的，不能用于帮助定位其他传感器节点。在多级算法中，公共节点不需要直接与参考节点通信，一旦传感器节点被本地化，它们就成为新的参考节点，并且可以帮助定位其他传感器节点[15]。

TPS算法[16]属于多级算法。在该算法中，存在3种类型的节点，即表面锚节点、新参考节点和非本地化节点。先要定位靠近表面锚节点的传感器节点。一旦获得传感器节点的位置，就会计算出它们的置信度值并将其与置信度阈值进行比较。如果节点的置信度值大于置信度阈值，它们将成为新的参考节点，以帮助非定位节点定位自己，同时保持低定位误差。

根据定位算法中对于时间是否有同步要求，可以将定位算法分为2类：同步定位算法和无需同步定位算法[17]。对节点之间或者整个传感器网络进行时间同步可以增加定位的准确性，但是在时间同步的过程中会增加能量消耗。在许多情况下，本地化方案直接假设传感器节点彼此同步，然而，这在水下环境中难以实现，因此学者们提出了一些没有同步要求的定位算法[18]。

DHL算法[19]将定位问题转换为半平面交叉问题，是需要时间同步的。在文献[20]和文献[21]中，使用基于估计的AUV定位算法周期性地通过4个定向波束广播信息，以此来估计传感器节点的位置信息。节点接收信息并使用2个不同的连续波束来估计AUV在2个不同时刻的位置。然后通过使用2个估计的位置来获得节点的位置，是不需要时间同步的算法。

2 算法设计

本文算法分为3个步骤：1)利用TDOA测距算法计算信标节点与未知节点的位置，但是TDOA测距算法会因为海洋环境造成的水声信号传播速率不稳定而出现定位误差；2)利用LSTM对TDOA测距算法计算出的定位进行位置信息修正以提高定位精度；3)通过改进多变定位算法对测距修正值的利用实现对未知节点的精准定位。

如图1所示，白色圆代表未知节点，黑色圆代表信标节点。未知节点与信标节点在部署区域内随机分布。在部署区域内，未知节点向周围发出定位请求。周围信标节点接收到定位请求后，会随机选择出其中的4个信标节点响应该节点的定位请求。

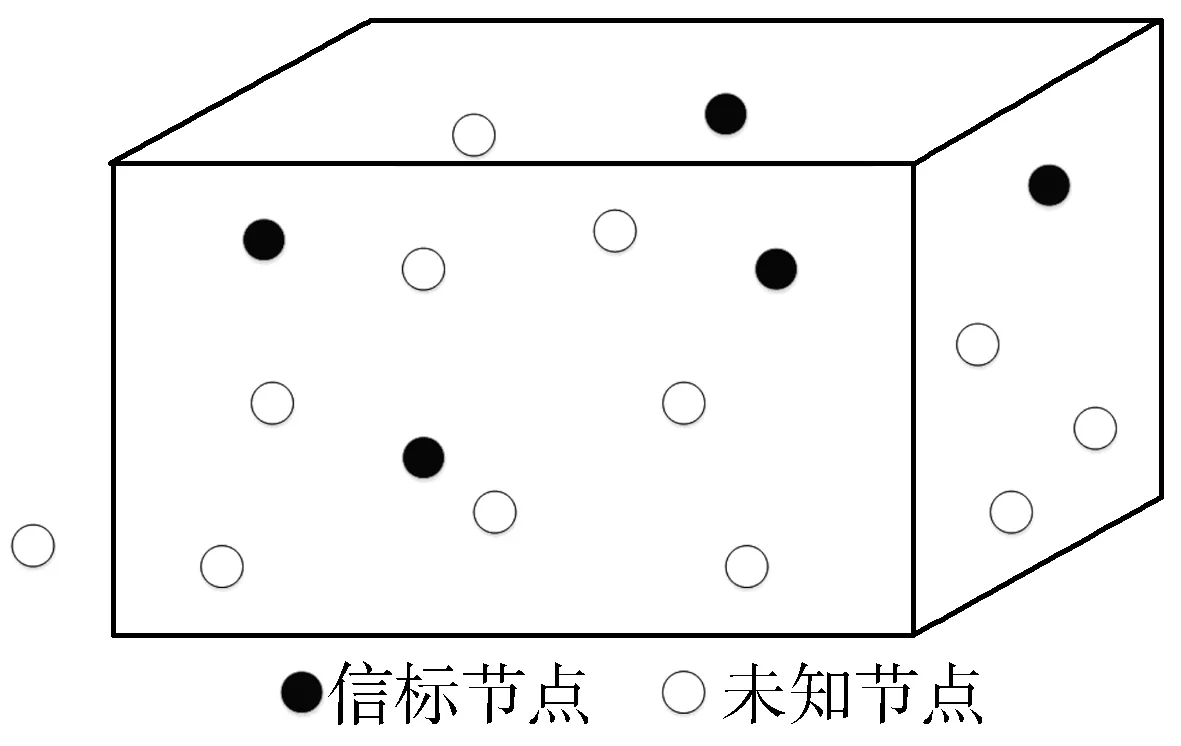
图1 节点分布示意图

如图2所示，假设在部署区域内，H1是发出定位请求的未知节点，D1、D2、D3、D4分别是被随机选择而出的信标节点，其位置信息分别是(x1,y1,z1)、(x2,y2,z2)、(x3,y3,z3)和(x4,y4,z4)。D1～D4这4个信标节点分别向未知节点H1发出快速率和慢速率2种信号。

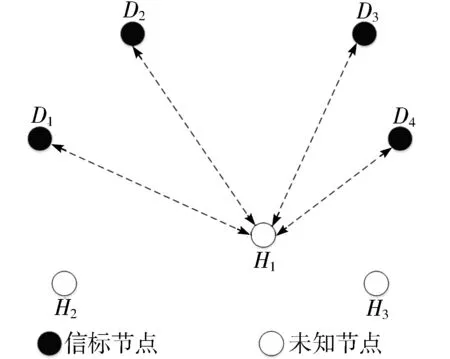
图2 信标节点响应示意图

图3以信标节点D1为例，D1在t0时刻向未知节点发出速率为c1、c2的2种水声信号，其中c1>c2。t1是速率为c1的信号到达未知节点的时刻，t2是速率为c2的信号到达未知节点的时刻。可以求出信标节点D1与未知节点H1之间的距离，即：

图3 TDOA测距示意图

(1)

其中n=1，2，3，4。L1、L2、L3、L4分别代表D1、D2、D3、D4到H1的距离。但是其中的水声信号传播速率深受到海洋环境的影响，公式为：

c=1449.30+0.16P+0.00029T3-0.055T2+4.6T+(1.34-0.01T)×(S-35)

(2)

其中，P表示水声信号传播时的环境压强，T表示水声信号传播时的环境温度，S表示水声信号传播时环境盐度。

水声信号传播速率的变化造成公式(1)的不准确和不稳定，所以，接下来使用LSTM进行测距修正。LSTM是一种非常善于处理时序关联性强、周期性强的循环神经网络结构，并且改善了传统循环神经网络(Recurrent Neural Networks， RNN)的信息不能长久传播以及前期输入数据权重随网络层数的增加而逐渐减小甚至消失的难题。

从公式(2)中不难看出，水声信号传播速率最重要的影响因素就是温度。温度和盐度会随着一年四季的变化而出现上下起伏，其中温度变化比较明显，盐度变化微弱，压强基本不会变化。

如图4所示，输入层、循环隐藏层和输出层共同组成了LSTM神经网络，其中循环隐藏层中的记忆模块是与传统RNN最大的不同之处。这些记忆模块包含输入门、遗忘门和输出门3种处理单元(即控制门)，LSTM利用这些不同处理单元对记忆模块的状态进行操作。记忆模块中的输入为当前时刻输入变量xt与上一隐藏层输出ht-1，输出为当前隐藏层状态ht。

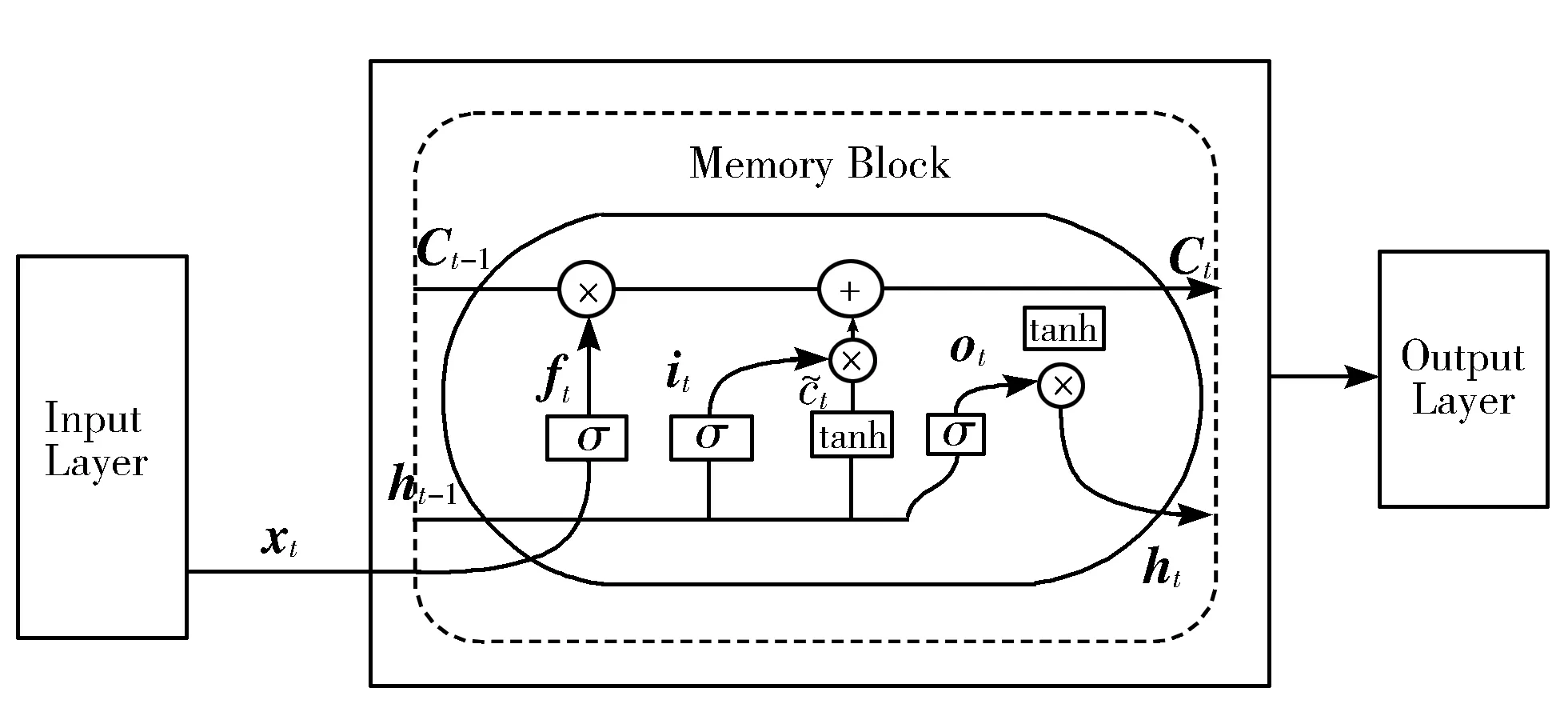
图4 LSTM循环神经网络结构图

除此之外，为了保持与前期数据的关联性并且防止前期数据权重下降，记忆模块经过计算后将细胞状态Ct传递给下一个记忆模块，以此平衡训练数据的权重。并通过以下迭代公式预测修正测距值：

ft=σ(Wf·[ht-1,xt])+bf)

(3)

it=σ(Wi·[ht-1,xt])+bi)

(4)

(5)

ot=σ(Wo·[ht-1,xt])+bo)

(6)

ht=ot·tanh(Ct)

(7)

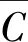
(8)

此时，设H1坐标为(xH1,yH1,zH1)，通过改进多边定位原理得出H1的位置信息。

qX=g

(9)

其中，

3 仿真实验

本节使用Python3.5模拟海洋环境对本文算法进行仿真，并评估仿真结果。水下仿真环境设置的长度、宽度和深度分别为1000 m、1000 m、500 m，海水温度和盐度分别设置为15 ℃和35‰。

首先分析LSTM模型的各个参数，先优化LSTM网络，将其调整为最优模型来预测测距修正值，再对本文提出的测距修正算法的定位精度进行评估。最后，通过算法对比验证本文算法在定位精度方面具有足够的优越性。

其中数据集中的海洋环境历史数据来源于中国气象数据网，包括时间、水温、水下压强和盐度。除此之外，在不同时间的环境限制下，进行随机点仿真得出在该环境中的TDOA的测距值与真实距离。将时间、水温、水下压强、盐度和测距值组成的五维向量作为一条数据，这条数据的标签为真实距离与测距值的差。整个数据集以7∶2∶1的比例分为训练集、验证集和测试集。

3.1 LSTM模型参数分析

本文使用回归平方和(R2)、平均绝对误差(Mean Absolute Error， MAE)、均方误差(Mean Squared Error， MSE)作为评价指标来评估Tanh、Sigmoid、Relu、Softmax和Linear这5种激活函数，将它们互相组合构成LSTM层和Dense层的激活函数。如果模型评价为负数且绝对值偏高则标记“×”，说明这个组合的模型效果非常不理想。

在表1中，将最佳组合标记加粗，即LSTM层采用Tanh作为激活函数、全连接层采用Linear线性激活函数。这个组合能够有效地丰富模型的表达能力，并使得模型可以逼近任意非线性函数。

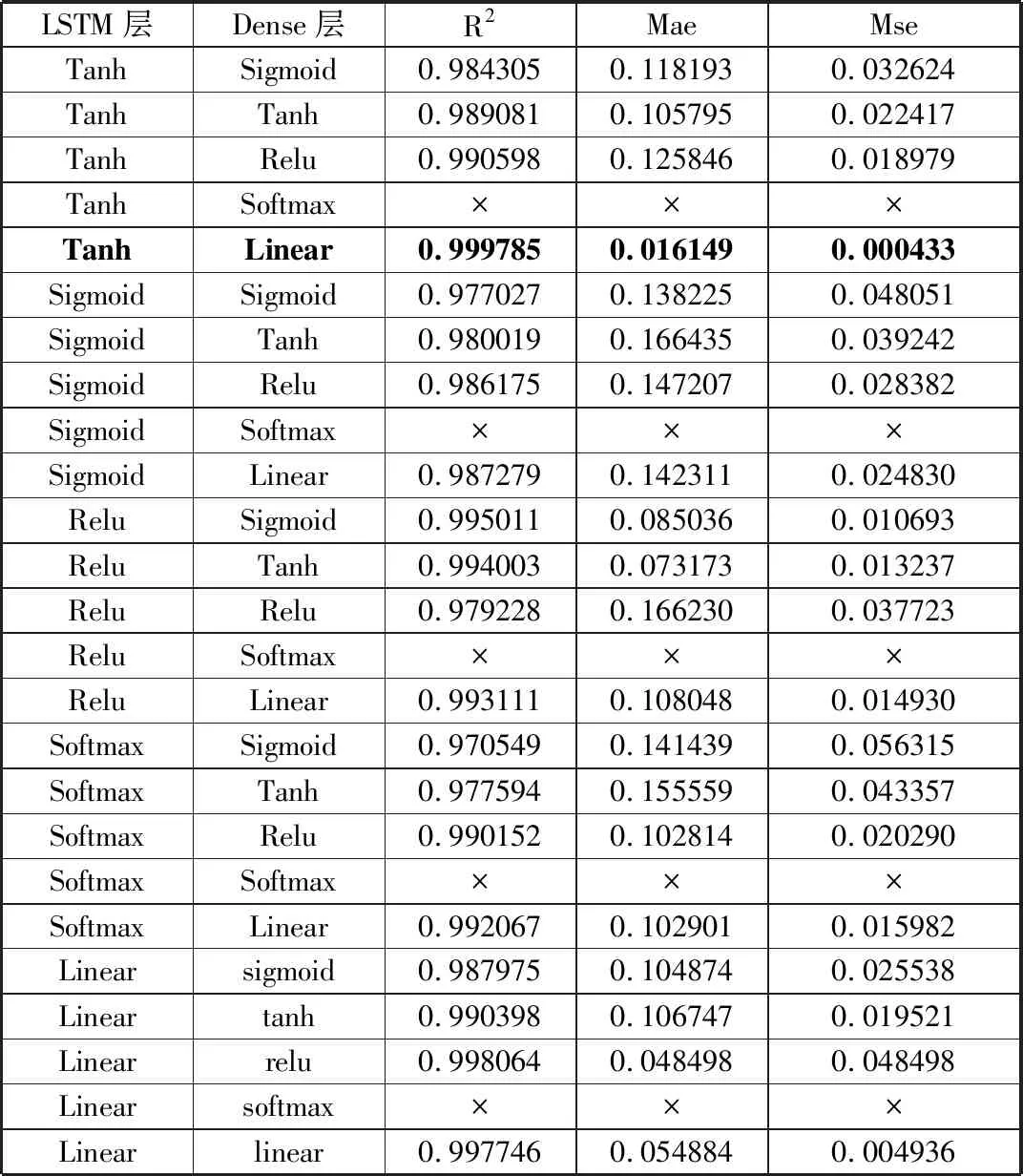
表1 不同激活函数对应的测距修正预测指标

针对部署区域的海洋环境数据集对SGD、Adam和RMSprop这3个梯度下降算法进行评估，其结果如表2所示。

表2 不同优化器对应的测距修正预测指标

由表2可知，模型选择Adam作为优化器时，各项指标都处于最佳。

选取上述最佳参数后，准确率变化曲线与loss变化曲线如图5、图6所示。

图5 准确率变化曲线图

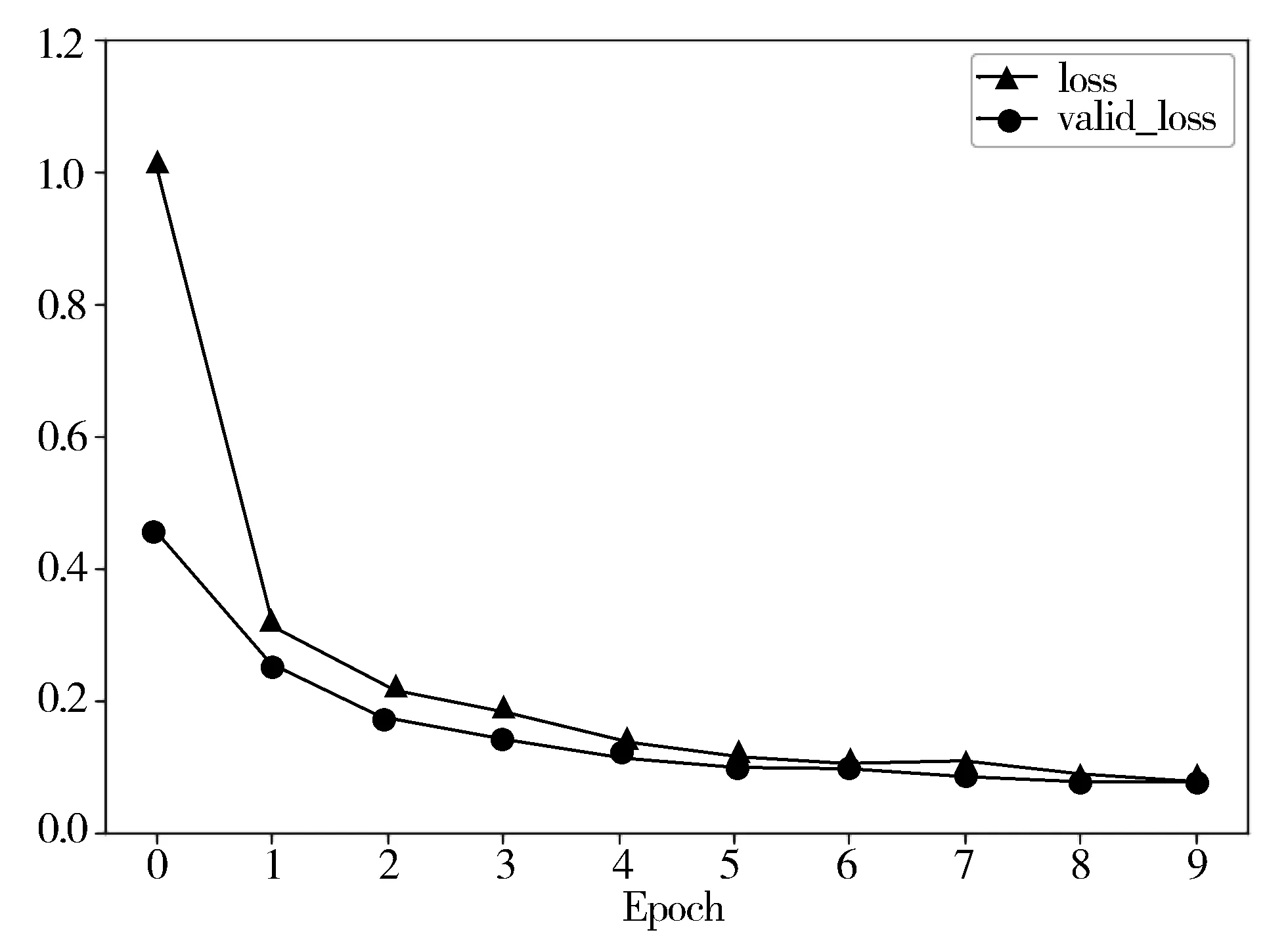
图6 loss变化曲线图

3.2 基于LSTM测距修正定位算法定位精度分析

经过上述实验之后，LSTM网络模型采用Tanh、Linear作为激活函数，以Adam作为优化器，学习率为0.001，数据输入格式为1×5的矩阵，输出为测距误差修正值。随后，在仿真环境中随机部署20个未知节点，并且利用本文提出的算法进行定位，其定位结果如图7所示。

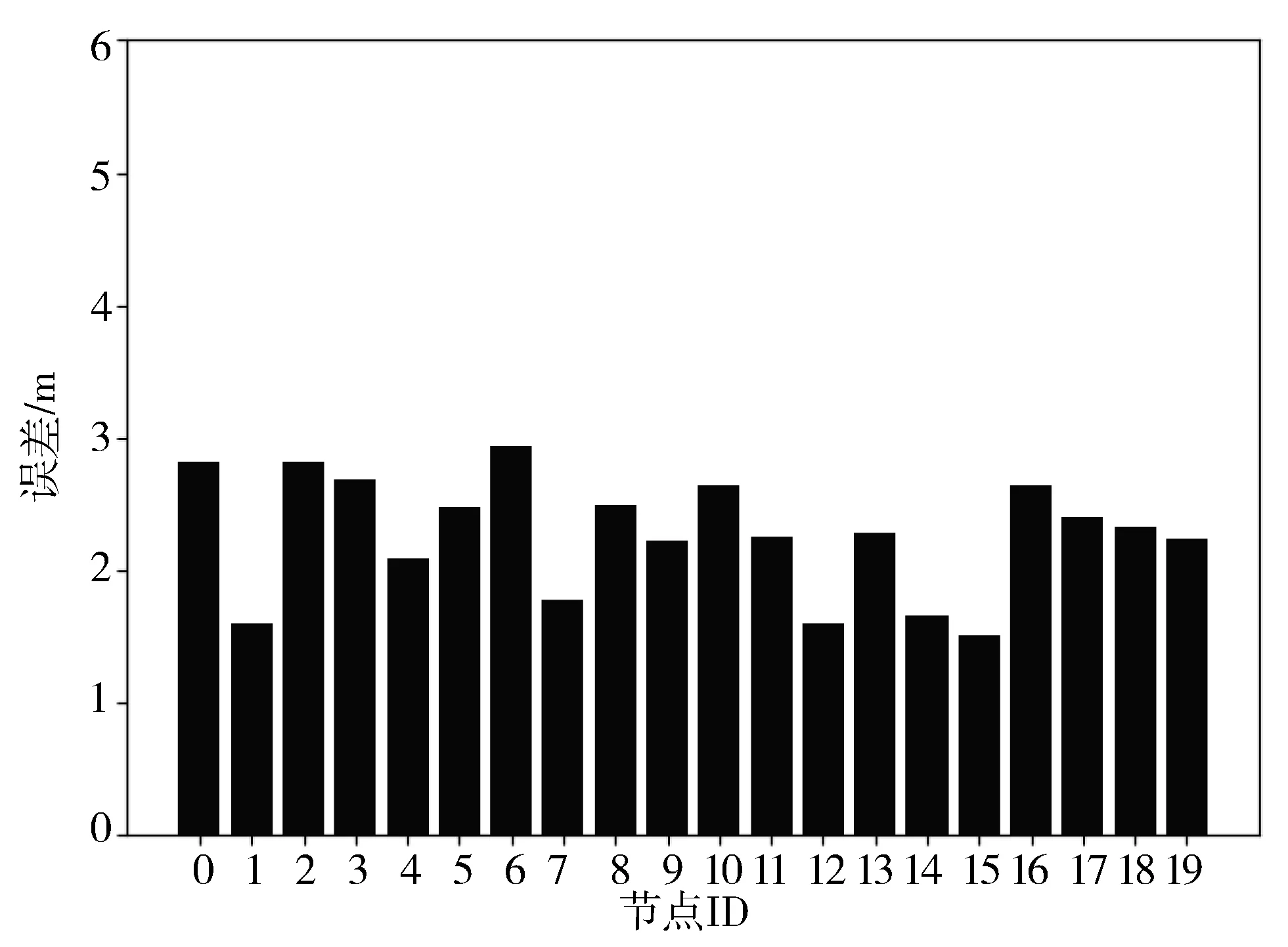
图7 随机节点定位误差分析图

从图7可以看出，本文提出的算法计算出来的定位结果误差集中在1.5 m～3 m之间，表明其定位精度比较优秀。误差之所以能够这么小的原因是TDOA的测距值经过LSTM优化之后变得非常准确，TDOA的测距值是经过本文改进的多边定位算法定位计算过程中的关键影响因素。

将图7的实验重复10次，并统计每次实验的平均误差，其结果如图8所示。每次实验的平均定位误差基本都在2 m上下浮动，表明该算法具有较高的稳定性。

图8 平均定位误差对比分析图

节点之间测距值的准确会消除许多其他定位影响因素，定位效果稳定的主要原因在于定位影响因素数量的减少，以及作为主要影响因素的测距值已经被优化得非常精确。

3.3 算法对比实验

对比算法选择的是基于GRNN的水下定位算法[21]与近段时间表现优秀的WTS算法[10]。GRNN与LSTM都属于循环神经网络，而WTS算法与本文算法都属于基于测距的水下定位算法。选择具有相似性的算法作为对比算法更有可比性，得出的实验数据更有说服力。算法定位误差对比如图9所示。

图9 算法定位误差对比图

从图9中明显可以看出，基于LSTM修正测距定位算法计算的定位误差普遍较低，而且上下起伏不明显；GRNN计算的定位误差偶尔能够与LSTM测出的定位误差相仿或者相近，但是其绝大多数的情况是远不如LSTM的，并且上下起伏较为明显说明稳定性、精确度都不如LSTM修复测距定位算法；WTS的定位精度不如基于GRNN的水下定位算法与LSTM修复测距定位算法。对比试验充分表明了LSTM修复测距定位算法的定位精度以及算法稳定性都比基于GRNN的水下定位算法和WTS算法高。

4 结束语

本文提出了一种基于长短期记忆网络测距修正的水下定位算法，利用LSTM修正信标节点与未知节点的测距，以此解决水下声信号传播过程中因环境因素改变其速率造成的测距不准确的难题，使得算法的定位精度明显提高。除此之外，通过LSTM改善TDOA算法并与改良的多变定位原理相结合使其能够快速准确地计算出未知节点的位置信息。