融合顶帽和Canny算子的电子束斑图像特征分析

王煜玺，袁晗，朱宗晓，何顺帆，田微

（中南民族大学 计算机科学学院，武汉 430074）

随着电子技术和现代工业的快速发展，大量的元件需要进行微米乃至纳米级加工.电子束技术［1］是目前较为合适的加工方法之一，其主要应用于高温合金的打孔、焊接等热加工和表面改性等电子束光化学加工［2］.

基于复杂背景［3］的图像处理问题是自动化图像处理领域的研究重点之一，但到目前为止，还没有学者对电子束斑图像进行较为系统的处理分析，人们对于电子束斑的检测往往通过肉眼观察其形状、大小、斑点分布情况来进行较为简单、直接的分析，并不十分精确.为了得到更为准确的电子束斑相关数据，本文采用图像处理的方法，对其进行轮廓检测等相关处理.

目前，深度学习和传统算法是较为主流的两种图像处理的方法. 文献［4］中基于深度学习提出的空洞卷积密集连接网络模型有效地缓解了梯度消失问题，增强了边缘特征.传统算法中的Canny算子凭借低错误率、边缘定位精度、单一边缘响应的优点，成为边缘检测的标准［5］.但其所使用的高斯滤波器无法很好地消除椒盐噪声，且需要手动设定高低阈值，在提取真实边缘时会存在误差.文献［6］中提出了用混合滤波器代替高斯滤波器进行了预处理，其优势在于其同时考虑像素点的空间域信息与值域信息，结合Otsu 算法，以图像的一维直方图为依据自动选取高低阈值.文献［7］中对Otsu 算法进行了优化，提出了基于侧抑制网络的二维Otsu 算法进行阈值分割，提高了对图像噪声的鲁棒性.

形态学梯度［8］边缘检测较为依赖选取的结构元素的形状和尺寸.相对而言，尺寸越小的结构元素越可以保护边缘细节，但降噪能力较弱，若选取的结构元素较大，降噪能力提升了，却丢失了边缘细节［5］.为弥补不同尺寸对检测效果的影响，文献［9］中提出了多尺度多结构元素灰度形态学边缘检测算子.而文献［10］中提出一种改进的多种结构元素多方向的形态学边缘算子，用三种结构单元分别对图像进行开闭运算、膨胀腐蚀操作和边缘检测操作，可以检测不同方向的边缘，使检测到的边缘更趋于完整.

上述文献中的算法对图像边缘检测都有着很好的优化，但并不完全适用于电子束斑图像的边缘检测. 因此，本文提出基于OpenCV 融合Top-hat 和Canny 算子的边缘检测算法对电子束斑图像进行整体轮廓检测，并通过轮廓的圆度D和轮廓宽度Width进行双阈值筛选目标轮廓，最终对目标轮廓图像进行等值切割，通过网格计数法提出电子束斑图像专用的均匀度标准.将得到的相关参数反馈给机器，以辅助电子束设备的实时改进.

1 基于电子束斑的特征分析

1.1 轮廓特征

电子束的研究，普遍以法拉第桶作为测量工具，由电子枪产生的电子经加速、聚焦，高速冲击到铝箔纸表面而形成电子束斑，如图1所示.在此过程中，铝箔纸表面在高温的作用下会产生形变，形成复杂背景，因而加大了图像处理的难度.

图1 电子束斑图Fig.1 Electron beam spot pattern

在复杂背景中提取电子束斑的轮廓时，首先需要对图像进行降噪处理，降噪后的图像可以提升识别处理的精确度.本文以降噪前后两幅图像的峰值信噪比（PSNR）和结构相似性（SSIM）进行降噪优劣的判别.若PSNR 值越高，则说明降噪后图像的失真越少，性能越好，若SSIM 值越趋于1，则说明降噪图像与原始图像的结构相似度越高，降噪效果越好［11］.

通过多种边缘检测算子对电子束斑处理的对比实验，Canny 算子得到的轮廓图像效果相对较优，但轮廓图像并不清晰且有大量的干扰轮廓，需要对其进行改进. 为了比较分析图像边缘检测的效果，本文采用了边缘检测性能品质因数［12］进行评价，其公式为：

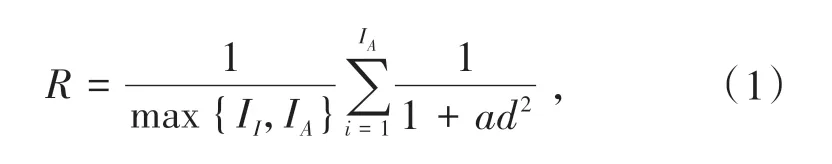
其中：II表示理想边缘图像中的像素和，IA表示实际边缘图像中的像素和，a为比例系数，通常取1/9，d为理想边缘到实际边缘点连线的垂直距离.若R的值越趋于1，则表明边缘检测效果越好.

1.2 圆度特征

在数学上，圆度D的定义为：

其中S表示轮廓内包含的面积，l表示轮廓的周长.当圆度D等于1 时，轮廓为标准圆；而对于其他形状的轮廓，圆度D都小于1，当轮廓越趋向圆时，圆度D越接近1［13］.

边缘检测的轮廓图像存在大量干扰轮廓，因此对电子束斑的轮廓图像进行轮廓宽度Width和圆度D的分析计算，并以Width和D的值作为参数进行双阈值提取目标轮廓.

1.3 均匀度特征

电子束斑的均匀度［14］，即为描述电子束的打点分布情况，但目前还没有明确的分析电子束斑均匀度的方法，因此本文将基于网格计数法提出电子束斑专用的均匀度检测标准.

其中网格计数法是Christiansen为描述喷管水量的喷灌均匀性提出的一个均匀系数［15］，其公式为：

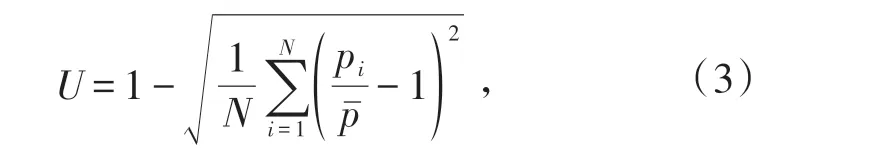
该方法是将检测区域均匀划分成N个小区域，计算每个小区域内均匀度点的个数n和整个区域点的个数m，则.

并通过检测的区域内pi的极差X反应电子束斑的分布及离散幅度，对上述的均匀度计算结果进行验证，公式如下：

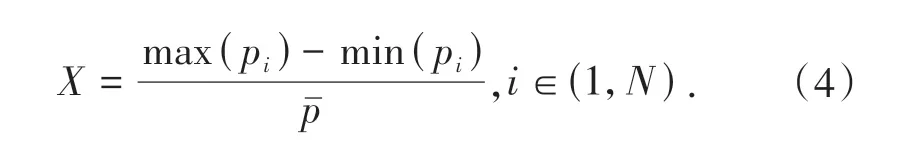
2 实验与分析

2.1 边缘检测的算法改进

2.1.1 Canny算子滤波器的选取

线性滤波中的均值滤波和高斯滤波与非线性滤波中的中值滤波和双边滤波是图像降噪中较为常用的方式.为了客观地分析四种滤波对本次研究对象的降噪效果，通过四组实验的峰值信噪比和结构相似性进行分析比较，如表1所示.

表1 滤波的PSNR、SSIM值Tab.1 PSNR and SSIM values of filtering

表1 中，双边滤波对电子束斑图像进行降噪后的PSNR 和SSIM 值均为最优，这是因为与其他滤波相比，双边滤波增加了一个基于空间分布的高斯方差sigma-d，结合了图像的空间邻近度和像素值相似度，同时考虑空域信息和灰度相似性，所以距离边缘较远的像素对边缘上的像素不会有很大影响，因此边缘附近像素值得到了较好的保存.

为验证实际效果，分别将以上四种滤波器融入Canny算子中，结果如图2、表2所示.

图2中使用双边滤波器进行降噪处理后的边缘检测轮廓，较其他滤波器处理的相对清晰，且从表2可以看出，由双边滤波器处理得到的边缘图像，其品质因数也为最优. 故本文以双边滤波器代替Canny算子中的高斯滤波器进行降噪处理.

图2 滤波对比结果Fig.2 Filter contrast results

表2 不同滤波边缘检测的品质因数RTab.2 The quality factor R of different filtering edge detection

2.1.2 融合顶帽的算法优化

数学形态学是建立在数学理论基础上的，以结构元素为几何模板探测和提取图像中物体形状的图像分析与识别的方法［16］. 其基本运算包括膨胀、腐蚀、开运算和闭运算. 设f(x，y) 为输入图像，b(s，t)为结构元素，Df和Db分别为f(x，y)和b(s，t)的定义域，则：

（1） 膨胀

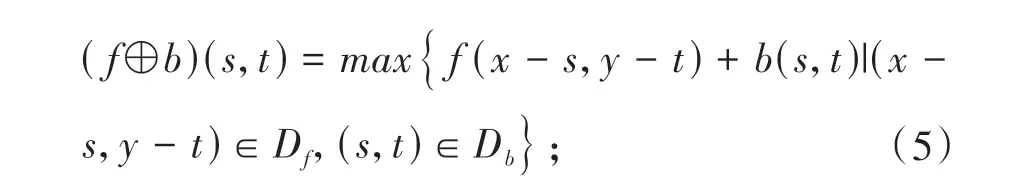
（2） 腐蚀

（3） 开运算

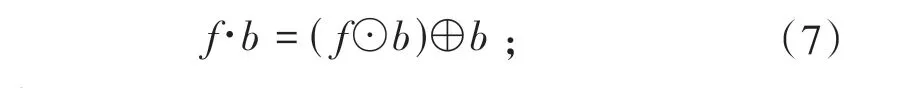
（4） 闭运算

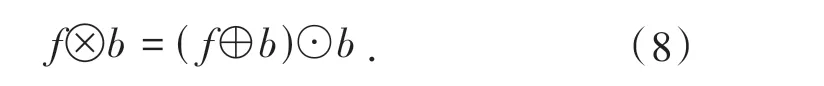
由于此次研究的电子束斑图像背景较暗，斑点轮廓较亮，故引入顶帽变换（Top-hat）做进一步处理.Top-hat 是原图像与开运算差的结果，它可以凸显出轮廓周围更亮的区域.

设g(x，y)为Top-hat的结果，其公式为：融合顶帽的对比，如图3所示.

图3 顶帽对比图Fig.3 Top-hat contrast

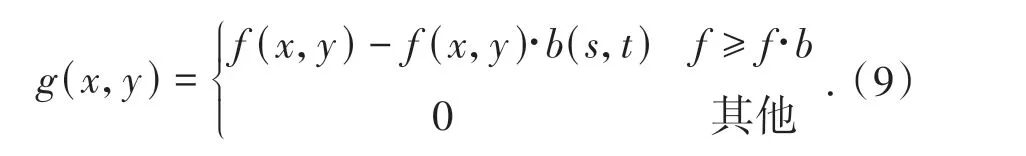
图3 中，融合顶帽后的二值图像（c）与图像（a）相比，填补了部分空白区域，同时使得边缘细节更加完整，在进行边缘检测时，图像（d）的边缘轮廓较图像（b）也更为清晰.

2.1.3 电子束斑图像的边缘检测

如图4所示，对于不同的电子束斑图像，本文的算法均可以得到其目标轮廓的清晰边缘.

图4 边缘检测图像Fig.4 Edge detection image

将本文检测结果与文献［6］和文献［9］中的算法检测结果进行比较，如表3所示，因为本文以双边滤波器代替高斯滤波器，较好地保留了边缘信息，同时Top-hat使得边缘更为完整，所以本文算法得到的结果的品质因数高于文献［6］和文献［9］的边缘检测结果的品质因数.

表3 边缘检测算法的品质因数RTab.3 The quality factor R of edge detection algorithm

2.2 目标轮廓的筛选

边缘检测得到的电子束斑边缘图像仍有较多的干扰边缘，但可以找到清晰的目标轮廓边缘，经观察可知大部分的干扰轮廓宽度较小且不规则，因此可以以轮廓Width值和轮廓的圆度D作为阈值对边缘图像进行筛选.

通过边缘检测图像找到每个小轮廓的外接矩形，并求其宽度Width值作为第一个筛选条件，利用圆度，计算每个小轮廓的圆度D作为第二个筛选条件，如图5所示.

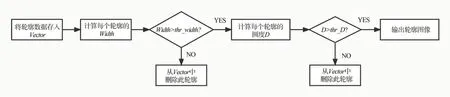
图5 轮廓筛选流程图Fig.5 Contour screening flow chart

目标轮廓圆度筛选结果如表4所示.

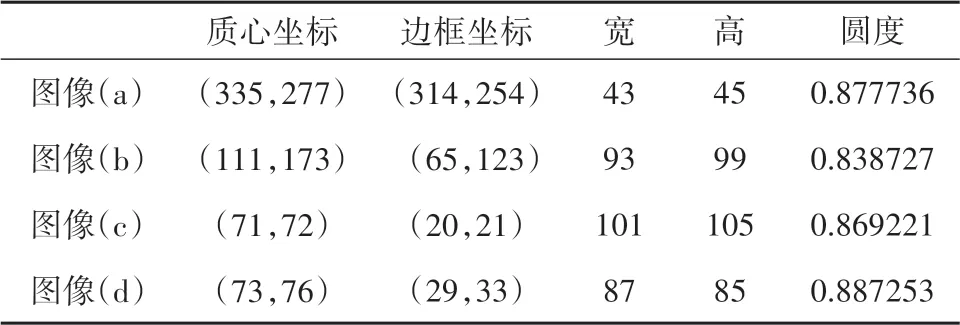
表4 轮廓圆度筛选结果Tab.4 Contour roundness screening results

经双阈值轮廓筛选，得到清晰且完整的目标轮廓图像，如图6所示.

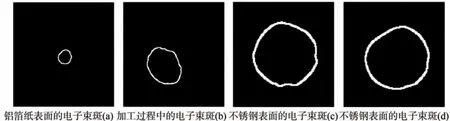
图6 轮廓筛选结果图Fig.6 Contour screening result diagram

2.3 电子束斑均匀度计算

基于网格计数法，考虑到电子束斑并非是正常的点集合，在打点的过程中会产生打点重合和点的形状大小不一的情况. 在此，提出一种计算电子束斑均匀度的标准：以轮廓内每个区域点集的像素值之和作为n，以轮廓内每个区域所包含点集的个数作为m.目的在于以平均像素值作为标准，减少因点集重合或单个点的大小和形状不一造成的误差.

本次研究将得到的轮廓图像的外接矩形进行3 × 3的等值划分，由于在边缘处有部分区域不在轮廓内部，在计算点集个数的时候需将这些点去除，而矩形内轮廓外以黑色作为填充，所以在累加像素值时可以不予考虑.

均匀度检测结果如图7和表5所示.

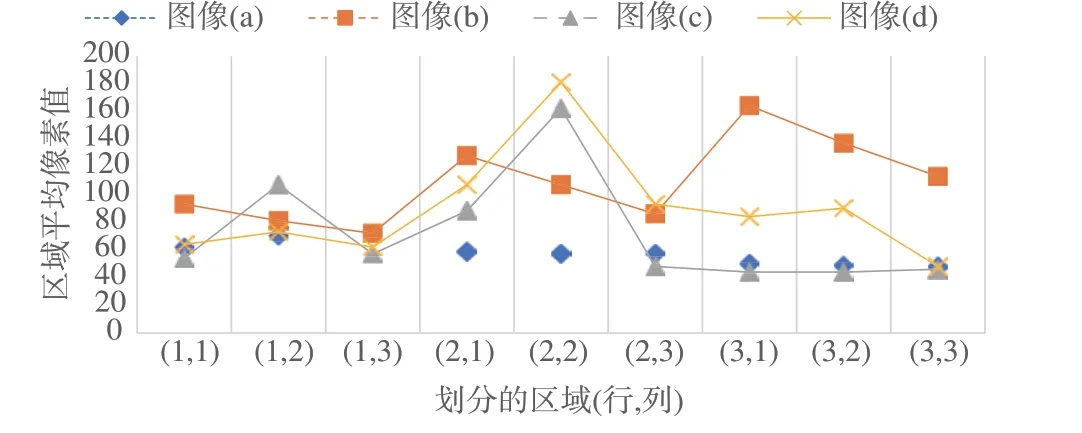
图7 区域像素值Fig.7 Area pixel value

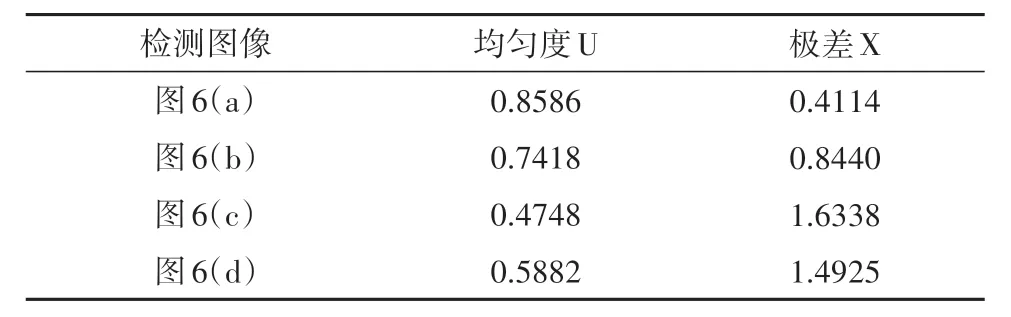
表5 均匀度及极差结果Tab.5 Uniformity and range results

结合图7 和表5 的数据，图6（a）的九个区域平均像素值较为接近，其极差较小，说明打在铝箔纸表面的电子束斑分布较为均匀且离散幅度较小，同时验证了其较好的均匀度的计算结果.图6（d）与图6（c）均为不锈钢表面的电子束斑，相比之下，图6（d）的均匀度更优.

3 结语

电子束斑图像的圆度和均匀度是电子束设备安装、检修、改造等过程中的关键指标参数，其反映了电子束技术效果的优劣.本文基于OpenCV 提出的电子束斑轮廓检测、圆度和均匀度计算的算法，取得了良好的效果，尤其对加工过程中的电子束斑图像有着显著的效果，有利于对加工过程的实时监测.通过网格计数法提出了一种电子束斑图像的均匀度标准，在无需精确点数的情况下，本文得到了准确的均匀度参数，并通过极差验证了其正确性.但是由于电子束加工的材料各不相同，使得电子束斑的背景不一且较为复杂，要实现完全的自适应轮廓检测，仍需要进一步对电子束斑的图像特征进行研究.可以通过深度学习的方法，寻找合适的框架结构对其进行切割训练，得到更优的结果.