一种基于可验证秘密共享的区块链共识算法

朱小强，郑明辉，乔译萱，陈珩

（湖北民族大学 信息工程学院，恩施 445000）

区块链技术是一种结合了密码学算法的去中心化分布式账本.目前，其研究主要分为两个方向：底层技术和场景应用.区块链系统在不同的场景下需要改进底层技术来满足不同的需求.共识算法作为区块链的底层技术之一，对保证区块链的安全性和效率起着至关重要的作用.根据参与区块链系统的节点权限的不同，区块链可以分为公链与许可链［1］.公链允许任何节点随时加入区块链系统并参与其共识过程，且链上的所有数据都是公共的.主流的公链共识算法包括工作证明（PoW）、权益证明（PoS）、委托权益证明（DPoS）等［1］.许可链中节点加入区块链系统需要提前获得确认，包括联盟链［2-4］和私有链［5］.私有链大部分被使用于集体和组织内部，不对外公开.而联盟链上的数据既可以是公共的，也可以是内部的，许可链的节点数量有限，数据访问权限管理更为严格，一般采用Paxos［6］算法解决分布式节点的一致性问题.Raft算法［7］是一种具有强一致性的类Paxos 非拜占庭容错算法，它将各分布式节点分为三种角色状态，即领导者（Leader）、候选人（Candidate）和追随者（Follower）.开始时，所有节点均以追随者状态进行相互投票，部分追随者节点通过投票变为候选人节点，当某候选人节点收到半数以上投票时变为领导者节点，其余候选人节点恢复为追随者状态.最终选定的领导者节点把客户机状态复制到追随者节点，并在收到半数以上追随者的确认后提交，即可完成日志复制过程，达成非拜占庭故障下的协商一致性.领导者节点定期向追随者发送心跳信号以证明其活跃性，一旦领导者发生错误或停止，一个或多个未接收到心跳信号的追随者将投票成为候选人并再次发起领导者选举.经过投票，新当选的领导者将继续进行区块的打包与交易过程.Raft算法的三种状态变更流程如图1所示.

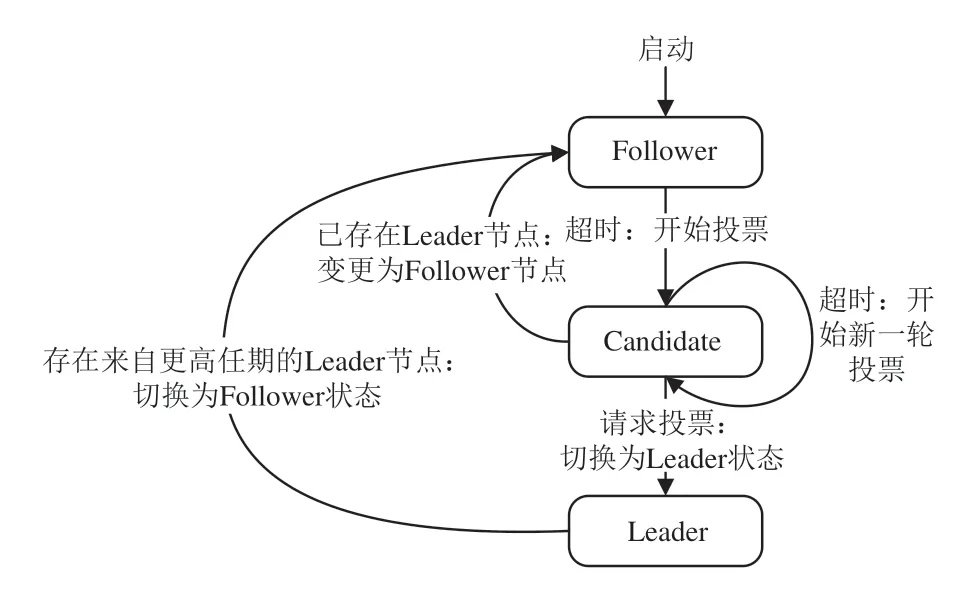
图1 Raft状态变更流程Fig.1 Raft state change process

联盟链由多个机构或组织形成的联盟来管理，在数据溯源［8］、档案管理［9］等领域有着广阔的应用前景，但其项目的真正落地需要解决其安全性差以及吞吐量小的问题.通常情况下联盟链中节点均被默认为已经确认，但实际情况中仍会有存在拜占庭节点的可能性，文献［10］提出，Raft算法中的拜占庭节点是指由于硬件故障或网络环境恶劣等原因，在点对点通信的传输信息过程中出现的有篡改通信内容等行为的节点.假如拜占庭节点成为记账节点，对于整个区块链系统是致命的.文献［11］提出了一种多轮Leader 轮值的Raft 共识算法，即让每个节点充分发表意见后再由小组长节点根据每个节点的意见及其他节点的修改意见进行最后统稿达成最终共识，算法将传统Raft 算法的通信复杂度从O(n) 提升为O(n2)；文献［12］中提出了一种结合RSA 签名和嵌套哈希［13］实现的Raft 算法，其通过牺牲一定的领导者选举效率和吞吐量来提高其选举安全性和拜占庭容错能力；文献［14］提出的BRaft算法保证了拥有最完备日志列表的节点才具备当选为Leader 的能力，利用SHA-256 算法进行日志项摘要生成，并通过RSA 算法对日志项摘要进行数字签名，最后对消息进行序列化与反序列化处理实现Leader 节点选举过程，但该算法在选举阶段增加了约一倍的时间消耗.

上述算法均针对Raft算法在Leader节点选举过程中的安全性进行了改进，但当节点数量上升时，共识延迟增加，选举效率有所下降.本文通过对Raft算法进行分析，提出了结合可验证秘密共享体制［15］实现的Raft 算法.利用安全性高的可验证秘密共享算法中子秘密分发过程取代Raft 算法中的Follower节点投票过程，通过验证承诺值取代Raft 共识算法中Candidate 节点的计票过程.该算法可以有效抵御恶意节点伪造选票攻击，实现了Leader 节点选举的拜占庭容错，提高了算法安全性，且维持了算法O(n)的通信复杂度，保证了算法可用性.

1 基于可验证秘密共享的Raft算法

秘密共享（Secret Sharing，SS）技术本质上是单一秘密的拆分管理.SHAMIR 在1979 年提出了(t，w)门限方案［16］，即通过构造一个t- 1 次多项式，将需要共享的主秘密S作为常数项，同时将主秘密碎片化为w个，分配至w个参与者，当碎片秘密数量大于或者等于t时，就可以求解出这个主秘密S.SHAMIR的门限方案解决了多方计算的数据隐私问题，但此方案的前提是所有参与者包括秘密管理中心都必须是诚实的，即当存在不诚实参与方时，对于一个秘密需要有相应的算法来验证其就是秘密的有效片段，否则不存在秘密可言.因此，FELDMAN［17］于1987 年根据SHAMIR 门限秘密方案及离散对数假设提出了一种高效的非交互式可验证门限方案（Verifiable Secret Sharing，VSS），即Feldman VSS.此算法中秘密分发者除了给出秘密的分片数据外，还要提供对应的系数承诺使得秘密碎片的数据可以被验证.

1.1 方案设计

本文提出的基于可验证秘密共享体制的共识算法是在Raft 算法的基础上加入FELDMAN 可验证秘密共享技术.利用可验证秘密共享中子秘密分发，承诺值验证和主秘密恢复的过程取代传统Raft共识算法Leader 节点选举过程中投票与请求投票以及计票的过程，加入秘密分发者角色进行初始主秘密的生成与分发，同时也保留了Raft 共识算法的三种节点状态，以及任期、随机超时时间的机制.此外，通过可验证秘密共享算法，以2/3 总节点数作为门限值，可以实现基于Raft算法的拜占庭容错.

基于可验证秘密共享的Raft算法状态转移模型如图2所示.其主要过程如下：

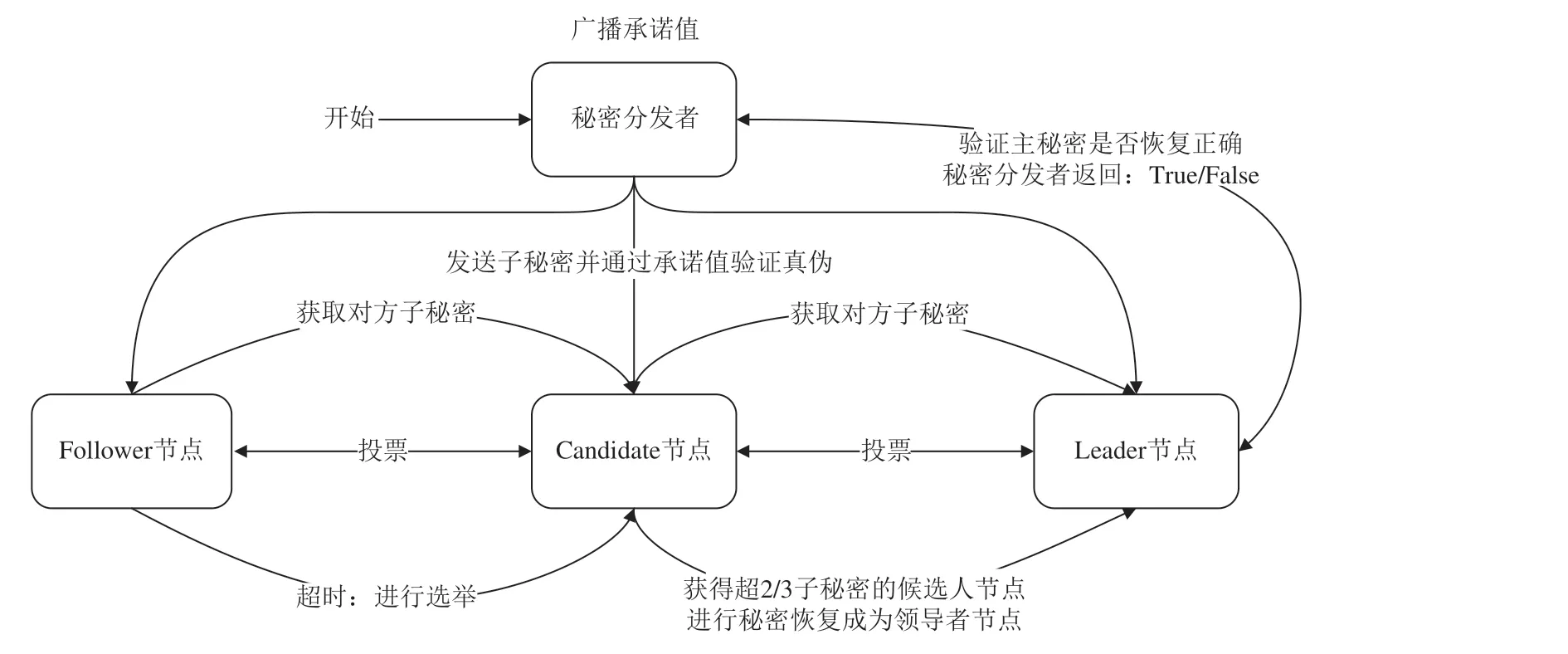
图2 基于可验证秘密共享的Raft算法节点状态转移模型Fig. 2 Raft algorithm node state transition model based on verifiable secret sharing

（1）秘密生成与分发阶段：Raft集群与各节点启动，秘密分发者生成一个主秘密、与节点数量相同的子秘密和承诺值，随机分发子秘密至各节点，同时广播承诺值；

（2）子秘密验证阶段：为防止秘密分发者作恶，各Follower 节点通过广播的承诺值验证收到子秘密的真伪；

（3）投票阶段：与Raft 算法相同，各节点在随机时间后超时，根据超时时间变更状态为Candidate，此时Candidate 节点向其他节点索要子秘密作为投票，首先获得大于2/3 总节点数子秘密的Candidate节点可恢复出主秘密；

（4）Leader 节点确认阶段：得到主秘密的Candidate 节点向秘密分发者提交其回复结果.若正确，秘密分发者广播其结果，此时各节点再次向此Candidate节点投票，获得最高票数的Candidate节点成为此任期的Leader 节点.反之选举失败，当前任期失效，并开始下一轮选举.

1.2 算法详细描述

本节主要针对改进后算法的详细流程进行阐述，算法伪代码如下：

29.产生Leader节点，共识完成.

Leader节点被确认后就开始为客户请求提供日志复制等服务，且Leader 节点周期性地向Follower节点发送心跳包来维持其领导地位.验证的交易在该任期内均由Leader 节点打包生成区块并在收到超二分之一节点回复后，发送确认信息至Follower节点，将该区块作为账本上的下一个区块，完成区块链账本日志复制过程.

2 算法分析

表1列出了Pbft，Raft算法及本文算法在适用环境，通信复杂度以及最大容错节点数的对比.由表1可知相比Pbft 共识算法，Raft 算法缺少了拜占庭容错的能力，而本文算法具备了3f+ 1 ＜=N的拜占庭容错能力，通信复杂度维持O(n).且本文改进的算法继承了Raft 共识算法原有的特性，在其共识效率及可用性未明显降低的情况下具有了抵御伪造选票攻击的能力与拜占庭容错能力.

表1 本文算法对比Raft与Pbft算法Tab.1 The algorithm in this paper compared with Raft and Pbft algorithm

2.1 安全性分析

所提出的算法解决了Raft 算法在Leader 选举过程中的安全性问题.利用可验证秘密共享体制取代了单一的选票计数方案，消除了不诚实的Candidate 节点导致的“虚假选票”的作弊风险，同时也修改了Leader 节点选举需要有大于1/2 非拜占庭节点进行投票的前提，将门限值设置为2/3 节点实现其拜占庭容错能力.并且可验证秘密共享体制相对传统秘密共享体制也做了安全性的提升，避免了秘密分发者作恶的可能性，利用广播承诺值的方式让每个节点确认其得到的子秘密是否真实.改进后的Raft 共识算法选举出的Leader 节点也进一步保证了其后续状态机复制的安全性.由于承诺值c被公开，即此密码体制的安全性是建立在离散对数问题难解性的基础上，所以它拥有计算上的安全性.

基于可验证秘密共享的Raft算法具有拜占庭容错能力，即只有当节点总数为N，拜占庭节点数量小于N/3 的状态下，非拜占庭节点的Candidate 节点可成功验证承诺值并恢复主秘密，切换节点状态为Leader，而当拜占庭节点超过设定的阈值时验证无法通过，需要重新进行选举及投票.当Candidate 作为拜占庭节点伪造选票时，由于秘密分发者采用广播的方式公布承诺值，任何节点均可验证子密钥是否真实，且承诺值具有计算上的安全性，所以此Candidate 节点不能利用虚假选票同其他节点的正确子秘密一起恢复正确主秘密，进而在广播主秘密时无法被其他节点承认为Leader 节点.以上特性使其拥有对抗伪造选票攻击的能力.

以上分析表明：改进后的共识算法具备拜占庭容错能力，可以抵御伪造选票攻击，符合算法安全性要求.

2.2 效率分析

Raft 算法达成共识的过程只需Candidate 节点与Follower 节点之间相互通信，达成共识之后的日志复制过程也只需Follower 节点与Leader 节点通信即可完成，Follower 节点之间无需沟通.当联盟链中总结点数为n时，Leader 节点选择过程的通信次数为n，日志记录过程通信次数为n- 1，所以其总通信次数为2n- 1，故算法通信复杂度为O(n).本文提出的算法中，选择Leader 节点的过程中广播承诺值，投票与索取投票的通信次数为2n+ 1，日志记录过程通信次数为n- 1，总通信次数为3n，所以算法通信复杂度同样为O(n).保持了算法的高效性.

算法活性是指共识一定能发生.Raft 算法的活性体现在其随机超时时间t的设定，t∈[150 ms，300 ms]且t远大于Raft共识中的消息时延.目的是保证有限时间内产生Leader 节点，且可以避免不必要的消息延迟导致的Leader 节点切换，保证共识系统的稳定运行.

本文算法完全保留了Raft算法对于保持算法活性的设计，若在t时间段内没有Leader 节点做出回应，则Candidate 节点重新启动选举，且较大的时间间隔也考虑到算法中存在的可验证秘密共享体制，预留时间给秘密分发，合成及验证过程.保证了算法活性.

3 仿真实验

为了评估改进后算法的性能，本实验着重研究了其领导者选举的效率，与传统Raft 算法进行了比较.评估指标为选举延迟即当Leader 节点宕机时重新完成选举所需的时间，以及改进后的联盟链每秒处理的事务数.实验测试中采用Python 语言实现Raft 算法以及改进后的可验证秘密共享算法，将两者结合实现了一种基于可验证秘密共享体制的共识算法. 实验测试平台采用8 核心16 线程AMD Ryzen（TM）7 4800H 处理器，16GB 内存的硬件平台.利用Python 配置轻量级web 框架Flask 模拟了联盟链中的多节点通信，操作系统为Windows 10 专业版64 位，测试软件为PyCharm 2021，Python 3.8，Flask 2.0.1.

图3 表示基于蒙哥马利算法对Feldman 可验证秘密共享算法进行优化后，当素数p分别为10bit 与12bit大小时，加解密及承诺值验证的过程中所需的时间（图中Montgomery-VSS 指基于蒙哥马利算法优化的可验证秘密共享算法；VSS 指原Feldman 可验证秘密共享算法）.从图3 可知：随着节点数及素数p的增大，原算法的时间消耗迅速增加，计算复杂度明显增大，当10 节点，素数为12bit 时，其时间消耗已大于50000 ms，应用在Raft共识算法中意义不大.经过蒙哥马利算法优化后的可验证秘密共享算法在大数条件下减少了取模的次数，简化了运算复杂度，效率提高约为原算法的850倍（随机素数取值为12bit，节点数7个以上时），同时节点数和随机素数p的大小对算法的计算难度影响较小，具有高扩展性，可以应用于Raft共识算法中.

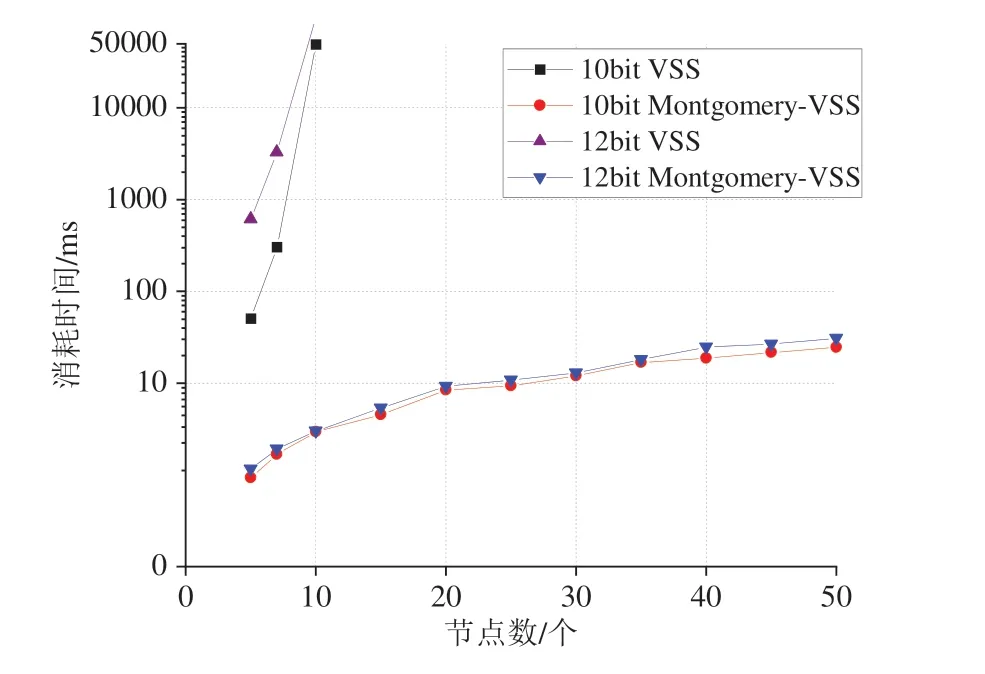
图3 蒙哥马利算法对加解密时间的影响Fig.3 The influence of Montgomery algorithm on encryption and decryption time

图4 表示当节点的数量为5 个到40 个时，两种算法下Leader 选举所需要的时间.随着节点数量的增加，传统Raft 算法的选举所需时间受节点数量影响较小.本文所提出算法中选举Leader 节点的时间随着节点数量的增加而增加.原因是节点必须对来自其他节点的提交进行等待与确认，而承诺值验证与秘密恢复过程的资源消耗也会因节点数量的逐渐增加而增大.

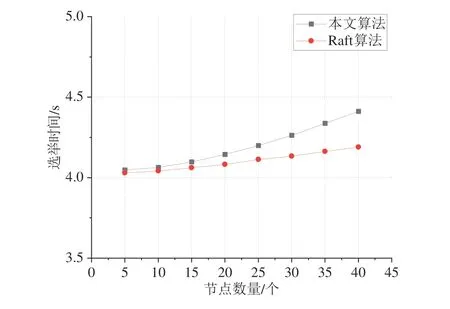
图4 开始状态Leader节点选举延迟Fig.4 The Leader node election delay in start status

图5表示了两种算法在节点数量为5个到40个且Leader 节点存在时，模拟Leader 节点在宕机时重新完成选举的延迟：在联盟链共识算法正常运行时手动停止当前实验中的Leader 节点，使两种共识算法分别重新自主选择Leader 节点，并在不同数量的节点存在时多次进行测试.结果表明，所提出的基于可验证秘密共享体制的Raft 算法能够保持高效率，但资源消耗略大于Raft算法.

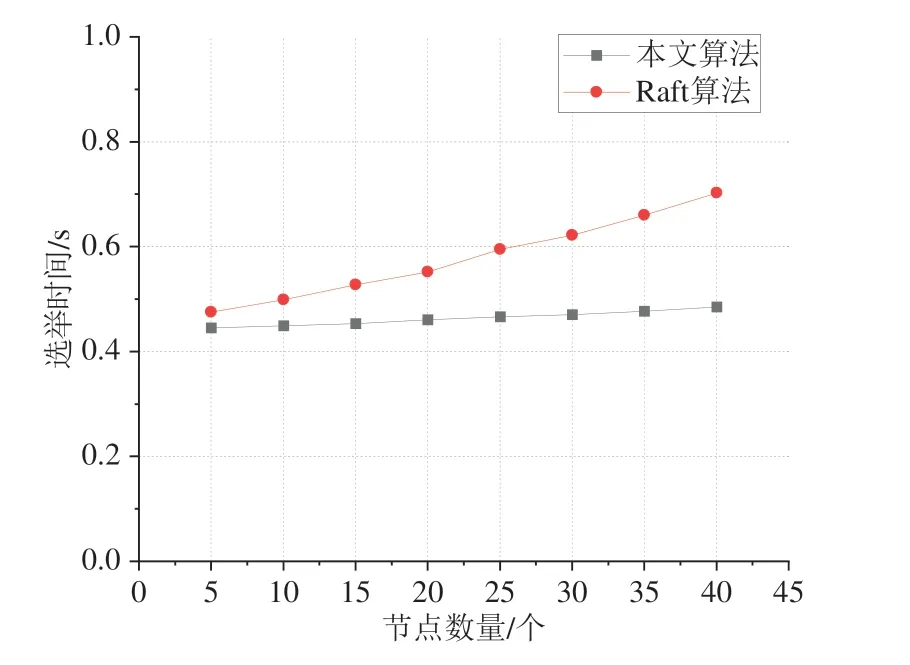
图5 宕机状态下Leader节点选举的延迟Fig.5 The Leader node election delay in outage states

由图4 及图5 分析得出，改进后的算法相比于非拜占庭容错的Raft算法在Leader节点的切换速度上有了约25%的性能下降，即Raft 算法与基于可验证秘密共享的Raft 算法的性能存在一定差异，随着网络中测试节点数量的增加，传统Raft 算法所受影响较小，但可验证秘密共享算法中对子秘密与承诺值进行的验证过程：

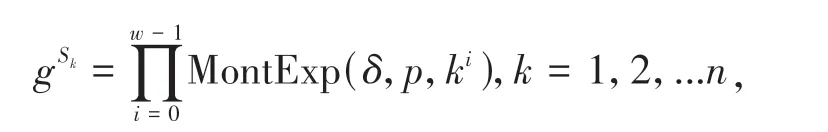
会消耗一定的计算资源，带来更高的选举延迟.

TPS（Transactions Per Second），即数据吞吐量是衡量程序性能的重要指标，代表单位时间内区块链能够处理的交易数量，图6 所示的测试结果中可以看出随着节点数量即其并发处理量的增加，两种算法中日志复制耗时均变长，数据吞吐量不断降低.但基于可验证秘密共享的Raft算法相比传统Raft共识算法，其吞吐量下降的比例从10%降低为4.2%.原因在于随着节点数量的增加，可验证秘密共享算法的计算成本相对于资源总消耗的比例逐渐变小，且由于其算法安全性保证了当选Leader 的正确性，避免了重复选举情况的发生.因此，基于可验证秘密共享体制的Raft算法更适用于对TPS要求更高的多节点场景.

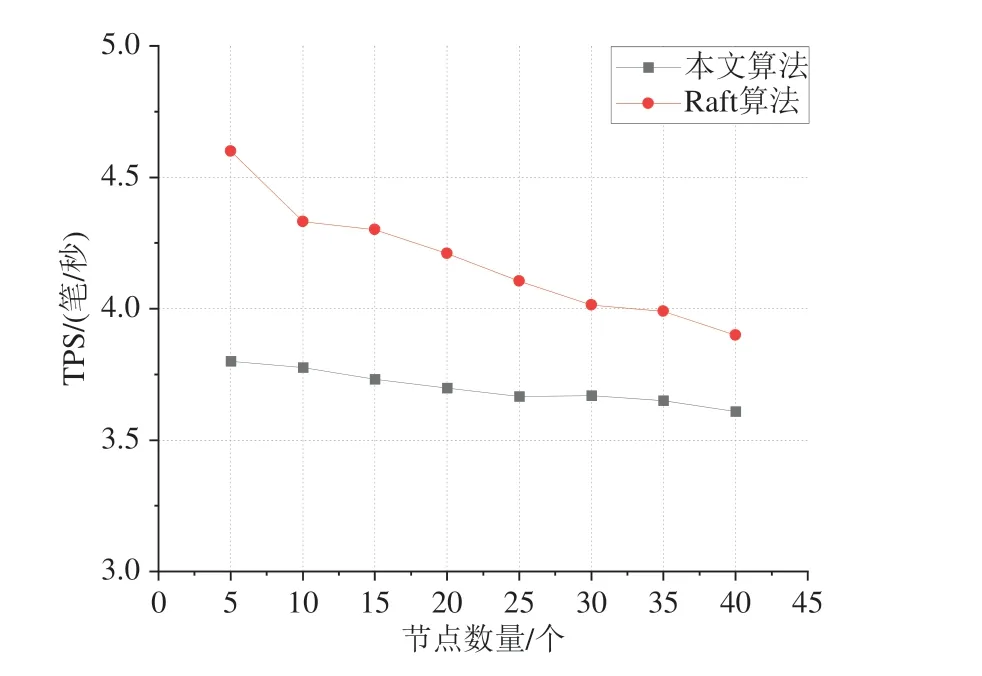
图6 数据吞吐量测试Fig.6 Data throughput test

4 结语

本文所提出的基于可验证秘密共享的共识算法是一种可拜占庭容错的Raft 算法，其利用效率改进的Feldman VSS 方案替代Leader 选举过程中投票与请求投票的步骤，解决了Raft 算法在拜占庭场景下Leader 选举中投票造假的问题，并结合常规Raft算法对改进后算法的安全性和效率进行了分析证明.实验结果表明，基于可验证秘密共享的区块链共识算法相比传统Raft算法拥有Leader节点选举过程中抵抗Candidate 节点选票造假的能力即拜占庭容错能力.并且相比非拜占庭容错的传统Raft算法，其主节点的选举过程仍然可以高效进行.综上所述，基于可验证秘密共享体制的Raft 共识算法是一种可以应用于联盟链中的安全性高，时延低，可容错的高可拓展性共识算法.