高速列车监测数据处理及故障诊断

苏宇婷，姚 琦，王昌冬，赵永玲

(大连机车车辆有限公司 柴油机技术部，辽宁省 大连市 116022)

随着高速列车运行速度的提高和服役时间的增加，列车动态运行环境快速恶化，车体的横向及纵向轮轨动力作用加剧，容易造成车体磨损和疲劳[1]。因此，对列车运行状态的反演识别、故障的诊断以及安全预警与健康维护运行状态进行分析，已成为高速铁路健康发展的重要研究课题。

车体故障监测信号为高维、非线性振动数据[2]。使用线性特征提取方法分析信号时，高维特征向量之间相互影响，产生冗余信息，分类识别效果不理想[3]。本文选择2种信号处理方法——小波包能量矩特征提取方法和流形降维学习方法。

1 信号特征提取方法

小波分析继承和发展了传统短时傅里叶变换的思想，同时克服了其窗口大小不随频率变化的缺点，提供了一个随频率而改变的时频窗口，根据小波系数就能检测异常信号，具有较强的局部分析能力，相比Fourier分析和短时傅里叶变换具有更显著的优点。而小波包可以将任何一个信号映射到一个由小波伸缩构成的一组奇函数上，并能保持信息的完整无损，并且对非平稳、非线性信号有局部化分析的能力。高速列车运行时产生的垂向振动大多是点头和滚摆等典型振动组合的复杂振动[4]，传感器监测得到的不同状态下的信号会表现出不同的频带能量分布特征。当系统参数发生变化时，其输出的振动信号能量的空间分布与正常系统相比会发生变化。如果利用小波包变换的多分辨率分析在多层分解后的不同频带内的信号，可以使原本不明显的信号频率特征在不同分辨率的若干子空间中以显著的能量变化形式表现出来，从而提取出能准确反映系统运行状态的特征信息。但这种传统的基于小波能量谱的方法没有考虑到各个分解频带上能量沿时间轴的分布特点，可能会导致提取的特征参数不能准确反映信号的特征，因此采用小波包能量矩的分析方法。

熵的概念是从物理学领域引入的，用于描述系统的复杂程度以及产生新状态的能力。熵的值越大，系统的复杂度越高，越紊乱，系统就越具有不规则性。本文将小波包能量矩和信息熵相结合，用于提取无规则非线性信号的复杂度统计特性具有很好的效果。

1.1 小波包能量矩特征提取

列车关键部件发生故障时，部分频带的能量发生变化，频带能量和故障状态存在映射关系，在不同状态下会表现出不同的频带能量分布特征[5]。小波分析有较强的局部分析能力，能够显示时频局部化特性，而小波包分解可以根据信号的特性自适应地选择频带相匹配。考虑到各个分解频带上能量沿时间轴的分布特点，引入能量矩参数。

对列车检测到的信号选择适当的小波基函数以及分解层数，再进行小波包分解。假设S表示初始信号，用Xjk代表j分解尺度下时间为k时的小波包分解系数。重构小波包分解系数，可以得出每个频带下的Sij。

通过计算得到每个频带Sij的小波包能量矩Mij：

(1)

式中：Δt——采样的时间间隔；

n——总的采样点数；

k——采样点。

构造特征向量，得出能量矩构成的向量T表示为：

(2)

式中：Mj——j分解尺度下Sjk的能量矩。

1.2 小波包能量矩熵

小波包能量矩熵是在具有局部分析能力的小波包分析基础上求其能量矩熵值，用于提取无规则、非线性信号的复杂度统计特性。

将振动信号分解m层并重构后，不同频段的小波包能量矩Mmj的划分测度pmj为：

(3)

其中，j=0,1,2,…,2m-1

(4)

式中：k——样本；

n——样本总数。

可以得到小波包能量矩熵的方程为：

(5)

将其归一化，令：

(6)

则小波包能量矩熵特征T′表示为：

(7)

式中：Hmj——m层j分解尺度下小波包能量矩熵值(j=0，1，2，3，…，2m-1)。

1.3 流形降维学习方法

流形学习(图1)是将在高维空间中复杂的数据通过非线性降维，保留其某种特定拓扑关系，找出嵌入在高维空间中的低维空间[6]。

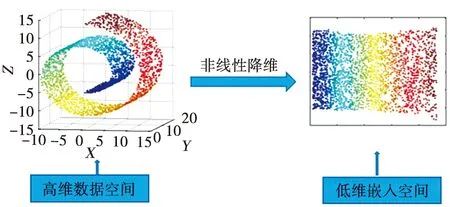
图1 流形学习示意图

拉普拉斯特征映射(Laplacian Eigenmaps，LE)算法是流形学习中局部分析方法，原理是在黎曼几何的框架内给出完整的几何分析，用无向有权图来表示一个流形结构，通过图像的嵌入性来寻找低维表示[7]。其基本思想是可以让在高维向量空间中欧氏距离非常近的点，在低维空间中的映射也很近。

1.3.1 构造邻域关系

1.3.2 求取近邻点的赋权值

假设W是权值矩阵，若i和j是相互连通的，可以得到Wij=1，否则Wij=0。

1.3.3 计算向量映射

求取图G的广泛意义上的特征向量以及特征值得到低维特征向量：

LY=λDY

(8)

可以转化为：

(9)

式中：Wij——样本i和j的权值矩阵；

Dij——矩阵Wij的正定对角矩阵。

2 列车监测数据介绍

本文利用车体上的传感器所监测到的振动信号，针对空气弹簧失气故障、抗蛇行减振器失效故障、横向减振器失效故障(采用全拆工况分别模拟抗蛇行及横向减振器失效故障)3种典型故障状态及其特征进行研究，监测数据采样频率为243 Hz，数据采集时间为1 min。图2为试验台数据结构图。

图2 试验台数据结构图

3 基于小波包能量矩的时频域分析

3.1 空气弹簧失气故障

当发生空气弹簧失气故障时，列车的垂向振动加速度增大，选取车体前枕梁上底板垂向加速度信号进行小波包能量矩时频域分析。图3～图5为不同速度下的空气弹簧时频域分析图。由图3～图5可知，正常工况下，列车在1～2 Hz有轻微振动，当发生空气弹簧失气故障后，垂向振动加剧，振动频率后移。在2～3 Hz期间，垂向加速度的振动幅值明显增大，其振动能量主要聚集在低频区域。当列车以不同速度行驶时，其振动呈现的规律一致，振动的频率区域没有发生变化，即列车振动能量的分布特征并不随速度发生改变。但速度越高时，空气弹簧失气工况的垂向加速度越大，振动能量越高。

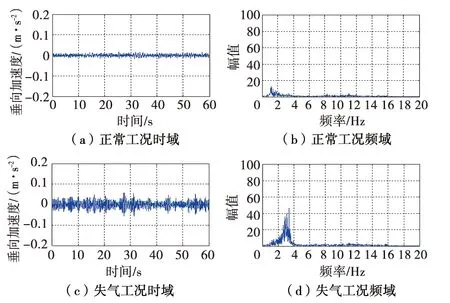
图3 80 km/h空气弹簧正常工况与失气工况时频域分析图

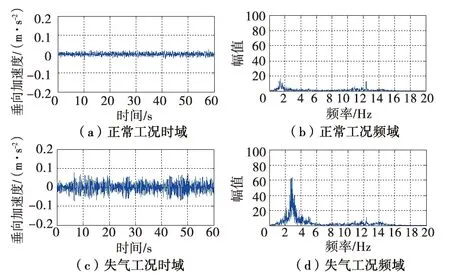
图4 160 km/h空气弹簧正常工况与失气工况时频域分析图

图5 220 km/h空气弹簧正常工况与失气工况时频域分析图

3.2 抗蛇行减振器失效故障

图6～图8为不同速度下的抗蛇行减振器时频域分析图。由图6～图8可知，列车出现抗蛇行减振器失效故障时，列车横向振动加速度增大，选取车体中部地板横向加速度信号进行分析发现，与正常工况相比，列车发生抗蛇行减振器失效故障时，车体的横向加速度信号振动频率有所增加，在8～9 Hz频率处振动能量明显增大。但是在速度为160 km/h时，8～9 Hz处

图6 80 km/h抗蛇行减振器正常工况与全拆工况时频域分析图

图7 160 km/h抗蛇行减振器正常工况与全拆工况时频域分析图

图8 220 km/h抗蛇行减振器正常工况与全拆工况时频域分析图

振动反而减小，分析原因是列车已经接近蛇行失稳，列车振动能量加剧，振动频率发生改变。在速度220 km/h时，列车出现全频段高能量振动，已经蛇行失稳。说明抗蛇行减振器对减弱列车横向振动有非常明显的效果，当列车处于高速运行时可以吸收较大的横向振动能量。

3.3 横向减振器失效故障

图9～图11为不同速度下横向减振器时频域分析图。由图9～图11可知，横向减振器出现失效故障时，其故障情况与抗蛇行减振器失效情况比较相似。经分析，选取对该故障特征反应敏感的后中心销与拉杆连接处横向加速度信号进行研究。当列车发生横向减振器故障时，车体横向加速度信号的振动频率在8～9 Hz处出现了较大的幅值变化，振动能量明显增加。随着列车运行速度的不断提高，列车横向振动幅度较大的频率位置出现前移，振动能量增大。与抗蛇行减振器全拆工况在时频域分析上较为相似，横向减振器也对减弱列车横向振动有着非常明显的效果。

图9 80 km/h横向减振器正常工况与全拆工况时频域分析图

图10 160 km/h横向减振器正常工况与全拆工况时频域分析图

图11 220 km/h横向减振器正常工况与全拆工况时频域分析图

4 基于LE算法的列车状态估计

对正常工况与其他3种失效工况的数据，并提取其小波包能量矩熵作为初始高维特征向量，用流形学习中的LE算法对高维向量数据降至三维和二维进行分析。为了使分类的结果更加直观，在图中选用红色表示列车正常运行工况，绿色表示空气弹簧失气故障工况，蓝色表示抗蛇行减振器全拆工况，粉色代表横向减振器全拆工况。

4.1 空气弹簧失气故障

选取能体现空气弹簧失气故障的车体前枕梁上底板垂向加速度信号进行分析，图12为车体前枕梁上底板垂向加速度数据LE降维后三维、二维流形特征图。由图12可知，该通道信号可以区分空气弹簧失气故障工况(绿色)与其他3种故障工况的不同，说明空气弹簧失气故障对枕梁上底板垂向加速度有突出影响。不同速度下，特征分离效果不变，而速度并不会改变振动的规律，只是改变了振动能量的大小。

图12 车体前枕梁上底板垂向加速度数据LE降维后三维、二维流形特征图

4.2 抗蛇行减振器故障

选取能够体现抗蛇行减振器故障的车体中部地板横向加速度信号进行分析，图13为车体中部地板横向加速度数据LE降维后三维、二维流形特征图。由图13可知，该通道下可以分离抗蛇行减振器全拆工况(蓝色)与其他3种工况。在低速时，分离程度一般；速度升高，分离程度逐渐提高。二维流形特征图效果明显优于三维。同时，通过220 km/h的二维流形特征图可以看出，横向减振器全拆工况(粉色)也展现出分离趋势。这是因为横向减振器对于横向振动和横向加速度也有明显的作用。

图13 车体中部地板横向加速度数据LE降维后三维、二维流形特征图

4.3 横向减振器故障

选取能体现横向减振器故障的后中心销与拉杆连接处横向加速度信号进行分析，图14为后中心销与拉杆连接处横向加速度数据LE降维后三维、二维流形特征图。由图14可知，横向减振器全拆工况(粉色)分离明显。无论在高速还是低速情况下，都有很好的分离效果。低速时特征分散，高速时特征聚集，说明高速时振动表现集中。同样地，抗蛇行减振器全拆工况也展现出分离趋势，与上一节对车体中部地板横向加速度信号的特征降维结果相似。

图14 后中心销与拉杆连接处横向加速度数据LE降维后三维、二维流形特征图

5 结论

本文对安装在车体传感器采集到的原始振动数据进行预处理，得到有利于进行特征提取的振动信号，经过小波包的分解与重构提取小波包能量矩特征，对不同工况的小波包能量矩进行时频域分析。小波包能量矩特征熵值作为高维特征向量空间，结合流形学习方法中拉普拉斯特征映射算法降维，得到低维向量空间，低维特征数据用图像的方式直观显示，并对结果分析和评估。

小波包能量矩时频域分析了空气弹簧失气故障、抗蛇行减振器故障和横向减振器故障3种故障。空气弹簧失气工况下，列车纵向振动加剧，振动能量集中在低频区，且速度越高振动幅度越大，能量越高，能量分布特征不随速度发生改变；发生抗蛇行减振器故障时，列车横向振动加剧，速度升高振动幅度增大，振动能量增大；当列车发生横向减振器相关的故障时，结果与抗蛇行减振器故障相似，列车横向振动幅度变大，速度越高振动越剧烈。上述结论与列车结构分析和动力学分析结果相吻合。

针对4个不同工况的识别，采用流形降维学习方法中的LE算法对监测数据进行故障特征提取，可以发现：车体前枕梁上底板垂向加速度信号经LE算法降维后，对空气弹簧失气工况有明显区别于其他3种工况的效果，在低速和高速时都分离明显；车体中部地板横向加速度信号可以使抗蛇行减振器全拆工况分离出来，速度越高分离越明显，同时在高速时，横向减振器全拆工况也有分离的趋势；后中心鞘与接杆连接处横向加速度信号可以体现横向减振器故障，速度越高分离越明显，在高速时，抗蛇行减振器全拆工况也完全分离。这说明空气弹簧对垂向振动和垂向加速度有影响，抗蛇行减振器与横向减振器对横向振动和横向加速度影响较大，由此验证了动力学分析的结论。

对列车振动信号采用小波包能量矩熵的特征提取方法，再进行流形降维分析可以分离出正常工况与故障工况，直观快速地判断列车是否出现故障，对列车早期故障预警提供了帮助。同时，可以引入支持向量机的方法识别，选取适当的核函数，能够发现流形降维后的特征故障识别率明显高于高维特征，该方法有助于实现工况的有效识别。