基于有限元方法的悬空管道稳定性分析

王超，李小玲，吴玉国

基于有限元方法的悬空管道稳定性分析

王超，李小玲，吴玉国

（辽宁石油化工大学 石油天然气工程学院，辽宁 抚顺 113001）

自然灾害中的土体塌陷严重威胁埋地管道的稳定性。为了研究埋地管道在悬空塌陷区的稳定性，基于有限元方法，研究了壁厚、外径不同的埋地弯管在悬空状态下的位移、应变和应力；采用特征值屈曲理论，研究了一定条件下埋地弯管在土体塌陷时所能承受的极限长度。结果表明，减小管道在土体中的埋深、增大管道外径以及壁厚，可以有效降低管道在土体塌陷过程中的位移，管道的应力和应变均发生在塌陷区的中心和两侧固支端的位置；管道外径、壁厚的提高，可以在一定程度上抑制局部应力过高；埋地弯管在采空区的极限长度约为87 m，并且增大管道外径和壁厚可增强埋地弯管在土体塌陷过程中的抗屈曲能力。

土体塌陷； 埋地弯管； 有限元； 屈曲特征值

石油天然气是人类赖以生存的重要能源，而管道运输在石油天然气输送方面具有显著的优点[1]，在世界范围内发展非常迅速。截至目前，全球在役油气管道数量约为3 800条，总里程约为1 691 300 km。对比十年前，长输管道已经取得快速发展[2]。当铺设石油天然气管道时，不可避免地会遇到河流、山谷等障碍物[3]，管道经过的地质地貌复杂，地理环境特殊，经常会出现断裂、滑坡、崩塌、泥石流以及悬空等各种问题，最为典型的是兰成渝成品油输送管线[4]。地质灾害轻则会造成管道裸露，重则会造成埋地管道的位移、悬空以及局部形变等，国内外发生过多起由于意外载荷导致管道失效的例子[5]。例如，1984年暴雨将铁秦管道冲开，造成管道悬空，约3 000 t原油泄漏到海水中；1999年洛河发生大洪水，位于西部的某天然气管道发生断裂，停输70 h。因此，对悬空埋地管道的研究刻不容缓。

1992年，W.K.Muhlbaur[6]详细叙述了管道安全保障评估模型和各种评价方法。王泸毅[7]基于Winker线性地基模型和Ranken土压力理论，利用有限元建立管土相互作用下的地质灾害模型，分析了管道受力情况和形变情况。由小川等[8]对地质灾害下受力情况进行了分析，并研究了灾害区埋地管道的应力和位移、管道埋深和悬空跨度曲线。王小龙等[9]利用埋地管道悬空部分与非悬空段之间的变形协调方程，得出管道跨中截面和管道内出土端的内力计算公式。康习锋等[10]对临界荷载进行线性拟合，得到了屈曲临界载荷的修正公式。单克等[11]建立了埋地管道失效概率模型，修正了6种基本失效因素并应用于长输管线上。

虽然对土体塌陷状态下的埋地直管进行的研究较多[12⁃16]，但对埋地弯管进行的研究相对较少。本文基于有限元方法，定量管道外径、埋深、壁厚等影响因素，研究了管道位移以及相应条件下的应力变化特征。基于线弹性屈曲响应，分析了特定荷载作用下管道几何参数对临界屈曲值的影响，以及悬空状态下埋地弯管的稳定性，以期为管道在黄土地区的安全运行提供参考依据。

1 研究方法

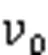
图1　土体塌陷埋地管道受力简图

埋地端示意图如图2所示。图2中，0为悬空管道的轴力，N；为塌陷宽度，m；为悬空管道与水平方向的夹角，（°）。

图2　埋地端示意图

悬空管道的挠度方程：

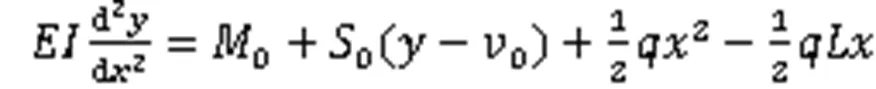
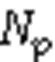
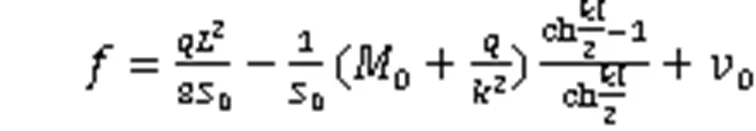
管道承受载荷：

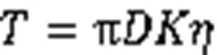
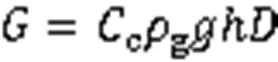
根据以上计算分析，单位管道方向受到的土壤荷载可表示为：

屈曲特征值理论是用来分析线弹性结构稳定性的理论。若该方法的预测结果与实际结果比较吻合，即可以认为通过求解屈曲特征值问题来计算临界荷载是合理的。模型对输出结果中的特征向量进行单位化处理，其最大值为1，将其输出的应力理解为相对应的应力分布。

2 有限单元分析

在铺设埋地管道时，根据实际情况，一般使用45°、60°、90°、120°弯管。其中，90°弯管最为常见。因为90°弯管使用量很大，对其进行研究具有现实意义。

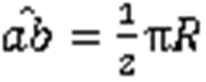
悬空管道与水平方向的夹角为、弯曲半径为的弯管，其弯曲部分的展开长度可按式（10）进行计算。

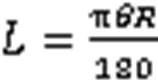
2.1 有限元分析

参考现有管道有限元分析实例，选用SHELL181单元或SOLID186单元进行比较分析。SHELL181适合分析薄或中等厚度的板壳结构零件。1个SHELL181单元有4个结点，每个结点有6个自由度，即沿、、方向的移动自由度和转动自由度。SOLID186是高阶三维20节点固体结构单元，具有二次位移模式，可更好地模拟不规则的网。模型包括土壤与管道两部分，由于土壤在模拟计算中选择SOLID186单元，所以具有更高的计算精度。本文的埋地弯管模型也适用于六面体单元划分，并且需要更高的精度。水平弯管的有限元模型如图4所示。

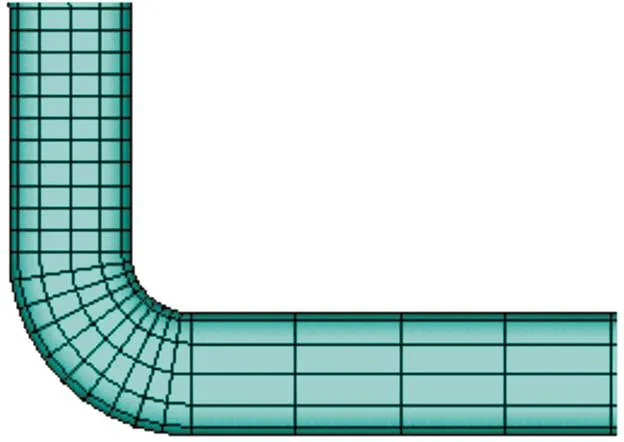
图4　水平弯管的有限元模型

2.2 网格划分及网格独立性检验

在模型的节点施加土体对管道的载荷，固支端管道与土壤为非线性接触，在模型横截面选取尺寸为90 mm×90 mm的正方形横截面，在埋地管道外表面所有节点施加均布载荷。设定弯管在土体的深入长度为3 m达到计算要求，并建立有限元网格模型，结果如图5所示。

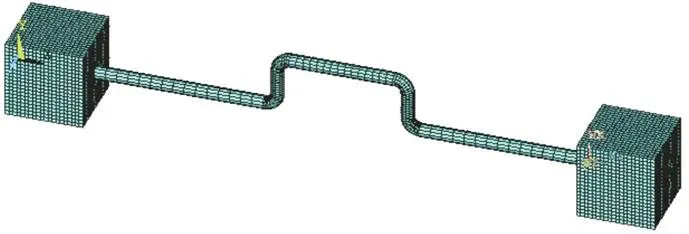
图5　实体单元有限元网格模型

为了提高计算的准确性，采用六面体网格划分。取管径0.965 0 m、壁厚0.013 3 m、埋深2.0 m、湿陷区长度50 m、弹性模量为207 GPa、泊松比0.3，取土与土之间抗剪强度极限计算。经初分网格求得结果，与文献[13—15]中的实例进行比较，对偏差部分进行网格细化，重新求解。经模拟计算，当网格尺寸小于等于90 mm×90 mm时结果趋于稳定，得出的最大位移偏差约0.28%。由此认为网格足够，因此选择该网格进行计算。

2.3 物性参数

为了使结算结果对实际工况有一定参考意义，根据《天然气输送用产品规格》（GB/T 9711.1—1997、GB/T 9711.2—1999、API 5L标准）选取管材基本参数建立模型。设定管道埋深为2.0 m，工作压力为2 MPa，分别计算管道外径为0.500、0.675、0.824、1.008、1.214 m，壁厚为0.015 0、0.017 2、0.019 4、0.020 6、0.021 6 m的条件下管道的位移、应力及应变。土体基本物理力学参数见表1，管材基本参数见表2。

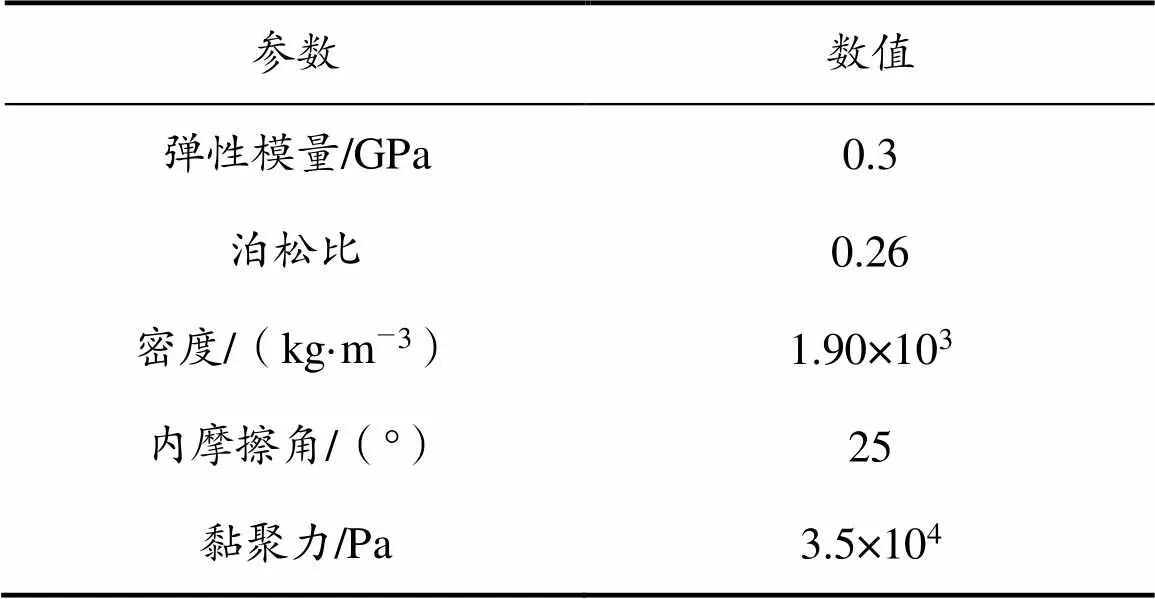
表1　土体基本物理力学参数

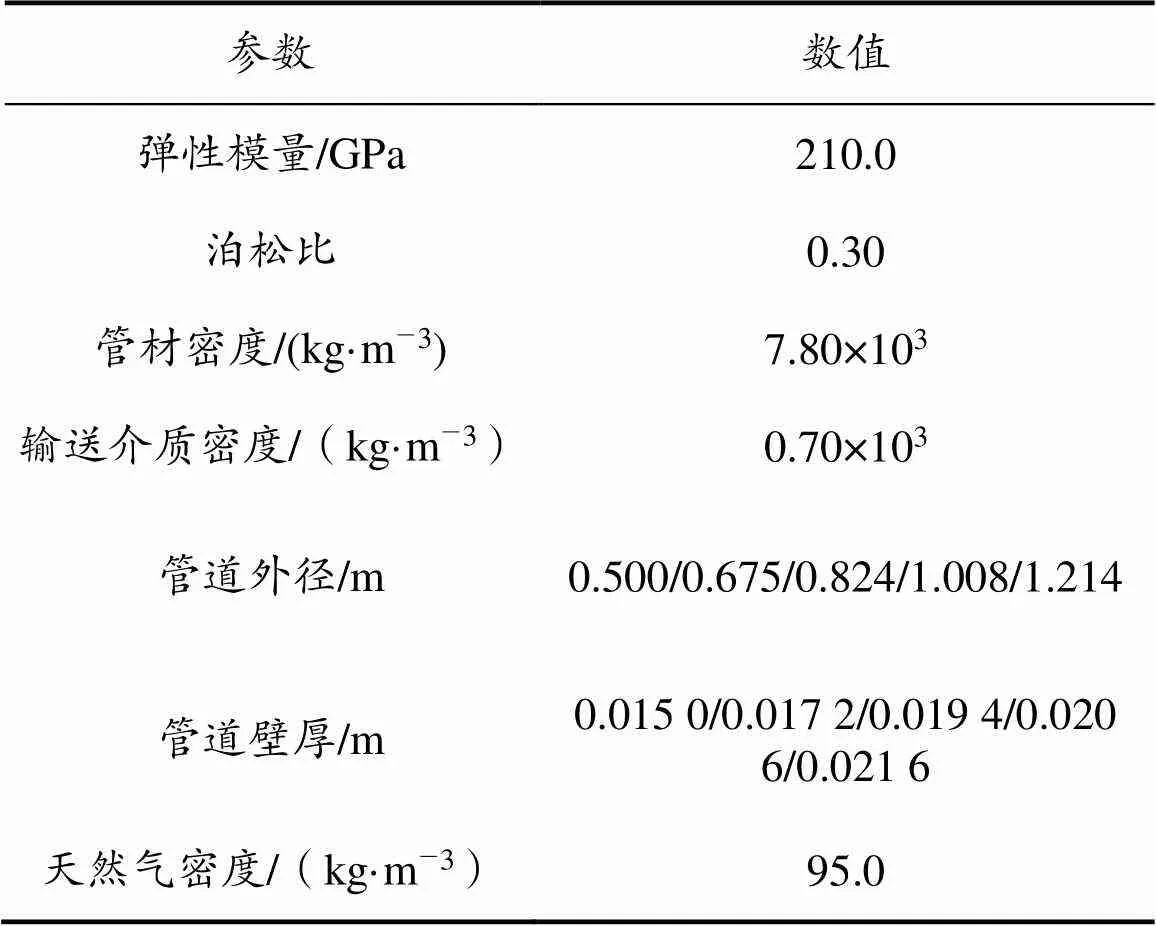
表2　管材基本参数

3 结果与分析

3.1 位移分析

管道埋深为2.0 m时外径不同的管道在土体塌陷过程中的位移如图6所示。由图6可以看出，小口径管道更难抑制塌陷时产生的位移，管道外径越小，管道最大位移增速越快，且位移峰值出现在塌陷区中心位置以及两端位置。在管径小于1.000 m时，这种变化趋势更为明显。外径为0.500 m的管道其最大位移为1.075 0 m，当外径增加到0.675、0.824、1.008、1.214 m时，管道最大位移分别降低了22.87%、36.23%、11.97%、5.41%。由此可知，当管道外径径大于1.000 m时，位移趋于稳定。

图6　管道埋深为2.0 m时外径不同的管道在土体塌陷过程中的位移

管道埋深为3.0 m时不同壁厚的管道在悬空状态下的位移如图7所示。由图7可以看出，壁厚更难抑制土体塌陷时产生的位移，管道壁厚越大，管道最大位移的增速越快，且峰值出现在塌陷区中心位置。壁厚分别为0.017 2、0.019 4、0.020 6 m和0.021 6 m时，最大位移的变化量分别为15.54%、29.67%、14.86%和8.94%。由此可知，壁厚增加到0.021 6 m时，位移逐渐稳定。

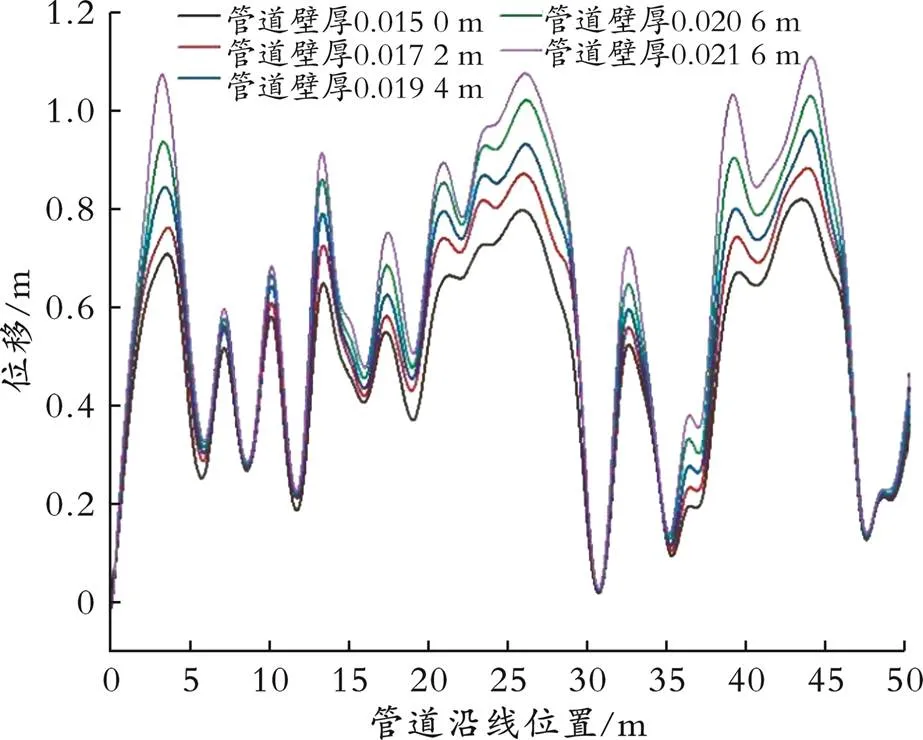
图7　管道埋深为3.0 m时不同壁厚的管道在悬空状态下的位移

埋深对位移的峰值也有影响，埋深不同时管道在土体中的位移如图8所示。由图8可以看出，都是在塌陷区的中心区位置出现峰值，从峰值来看，埋深每增加0.25 m，最大位移降低约6.00%。该模拟结果与文献[4]所得结论相符，存在误差的原因主要是受上覆土压力的影响。

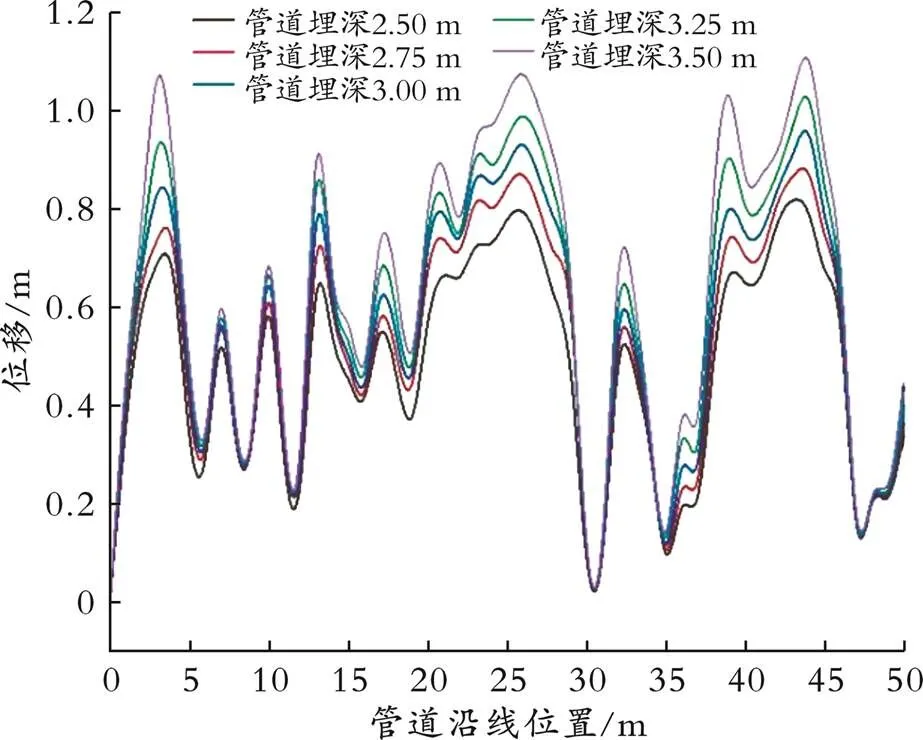
图8　埋深不同时管道在土体中的位移

3.2 应力应变分析

管道外径不同时的应力应变变化曲线如图9所示。由图9可以看出，埋地管道在土体塌陷过程中出现悬空状态时有较为明显的应力变化，而且在应力不超过1.0 GPa时，应力应变曲线变化的趋势很相似。在产生塌陷区位置中段出现小范围内的vonMises 应力峰值，经模拟计算出该范围为管道沿线的45～50 m处。外径为0.824、1.008、1.214 m的管道最大vonMises应力出现在埋地端的塌陷区，最大值未达到材料的屈服水平。管径大于1.00 m时最大vonMises应力突增，未塌陷区的最大应力增速明显快于塌陷区的最大应力。当管道应力的最大值超过0.600 GPa时，已经远远超过管道的屈服强度，接近管道的抗拉强度。应变曲线以塌陷区中心线近似呈轴对称分布，随管道外径的增加，管道的最大应变也随着改变，塌陷区的应变最大值出现在塌陷中心位置。该模拟结果与文献[4]所得结论相符，且塌陷区的应力和应变的变化趋势也与典型埋地管道灾害的力学理论相符合。

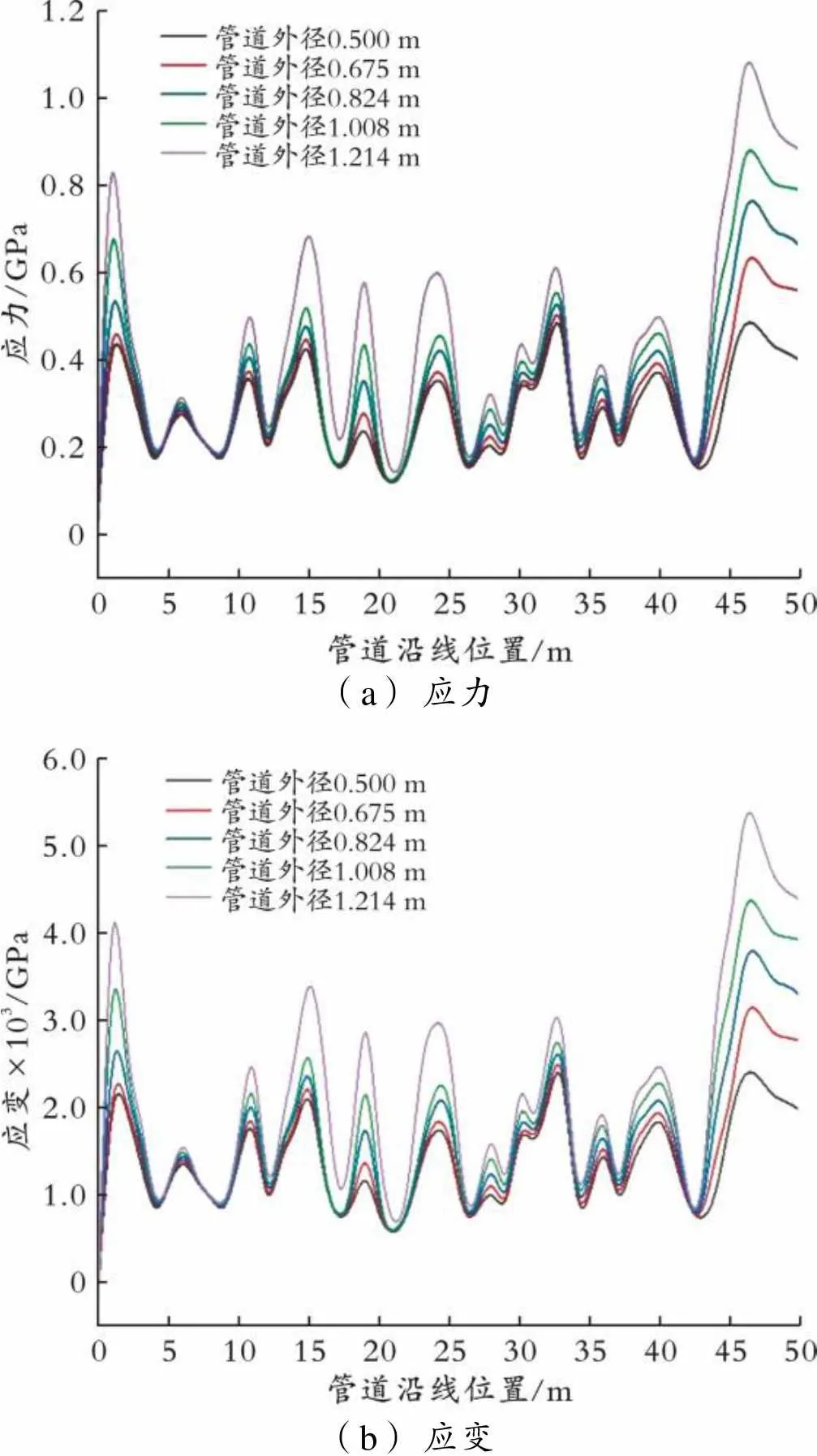
（a）应力 （b）应变

3.3 最小屈曲特征值分析

以外径0.500 m、壁厚0.015 0 m的管道为例，研究塌陷程度不同时管道的最小屈曲特征值，结果如图10所示。由图10可以看出，随着塌陷宽度的增加，埋地弯管的最小屈曲特征值呈下降趋势。根据屈曲特征值理论可知，当最小屈曲特征值小于1.0时，结构会发生失稳，由此可得管道在悬空状态下的塌陷宽度为87 m。

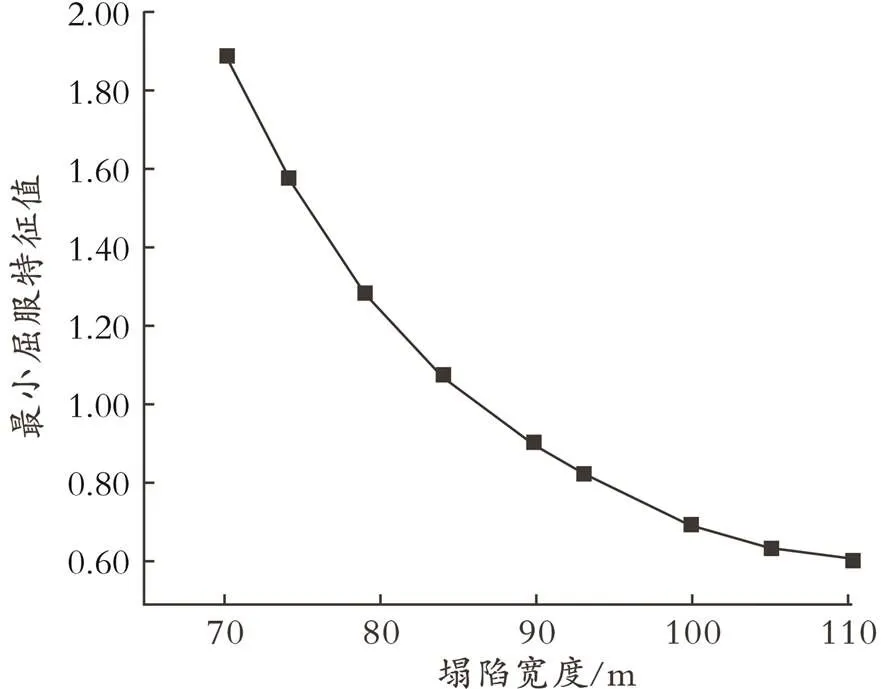
图10　不同塌陷宽度管道最小屈曲特征值

设定管道在悬空状态下塌陷宽度75 m，改变管道外径，分析管道最小屈曲特征值的变化趋势，结果如图11所示。

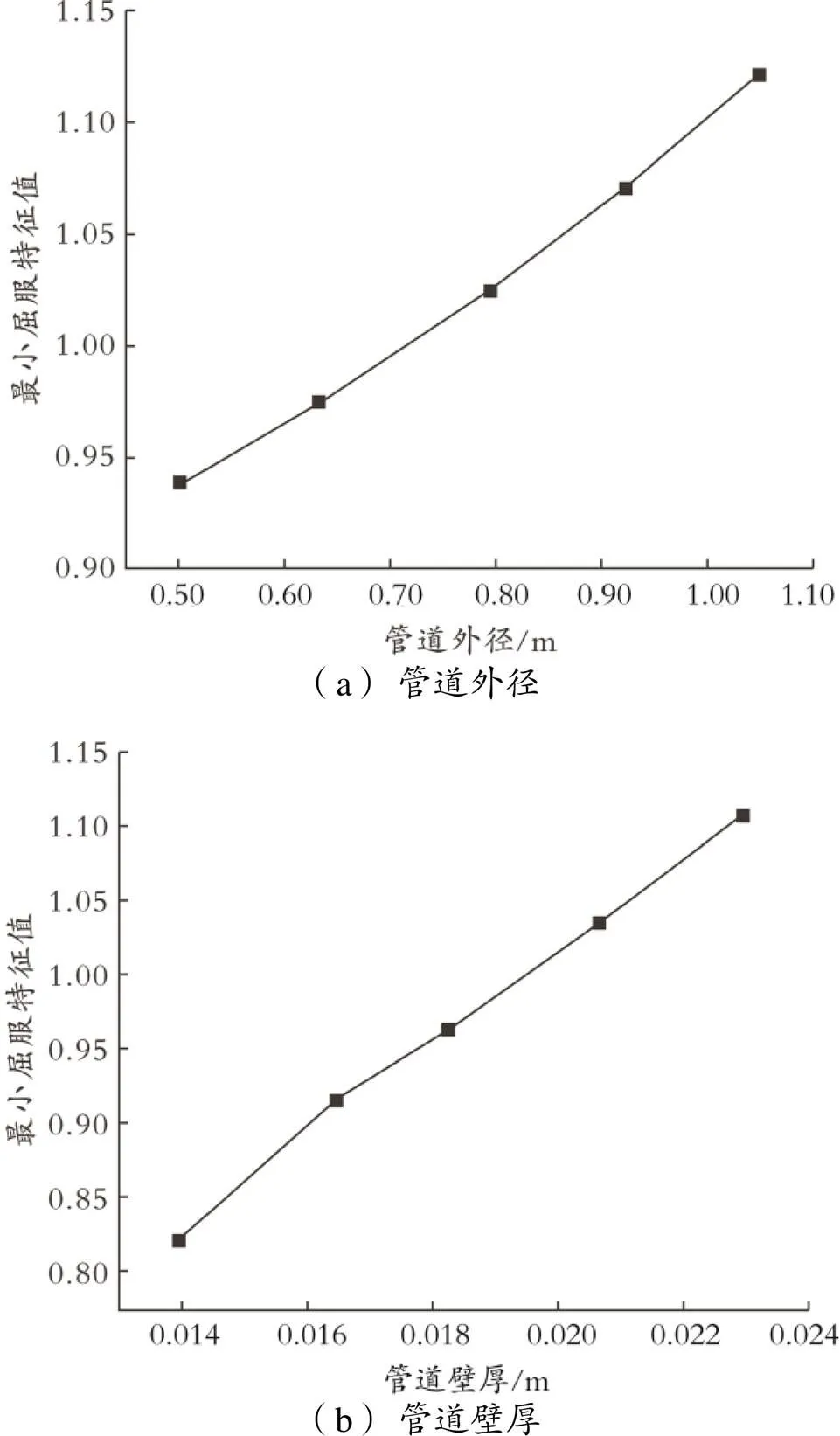
图11　管道尺寸对最小屈曲特征值的影响

由图11（a）可以看出，管道外径与最小屈曲特征值呈线性相关，说明管道外径的增加并不能改变管道的屈曲特性；当管道外径为1.008 m时，最小屈曲特征值为1.038，此时管道已接近临界屈曲状态。因此，当管道外径小于1.008 m时管道会失稳。

由图11（b）可以看出，随管道壁厚的增加，管道最小屈曲特征值增长趋势稳定。经计算可知，管道壁厚每增加0.001 5 m，最小屈曲特征值增加约6.00%，该模拟结果与文献[16]所得结论相符。基于特征值屈曲的判定方法，这一结论在文献[11—12]中得到应用。

4 结 论

（1）管道的最大位移出现在塌陷区中心位置。从位移峰值来看，管道埋深每增加0.25 m，最大位移降低约6.00%，埋深对管道的位移有限制作用。

（2）管道的最大von Mises应力与应变均发生在管道的埋地端，管道沿线45～50 m处，最大值已达到屈服强度，应适当选取大口径管道来提高埋地管道的抗屈服能力，以保证管道的安全运行。

（3）基于特征值屈曲理论，得到了埋地管道在土体塌陷时的最高悬空长度约为87 m；外径小于1.008 m时容易失稳。因此，可适当加大管道外径及壁厚来提高管道的抗屈曲能力与稳定性。

［1］ 王引真，雄伟，王彦芳.油气管道选材［M］.北京：中国石化出版社，2010.

［2］ 董绍华.全球油气管道完整性技术与管理的最新进展与中国管道的对策［C］//2006年全国失效分析与安全生产高级研讨会.北京：出版者不详，2006.

［3］ 王海燕，赵玲，吴明，等.基于ANSYS的跨越管道的有限元分析［J］.辽宁石油化工大学学报，2016，36（2）：25⁃27.

［4］ 张文彬.中国油气管道［M］.北京：石油工业出版社，2004.

［5］ 帅健，王晓霖，左尚志.地质灾害作用下管道的破坏行为与防护对策［J］.焊管，2008，31（5）：9⁃15.

［6］ Muhlbaur W K.Pipeline risk management manual［M］.Houston：Gulf Publishing Company，1992.

［7］ 王泸毅.输气管线在地质灾害中的力学行为研究［D］.西安：西北工业大学，2003.

［8］ 由小川，庄茁，张效羽，等.高压天然气管线在地质灾害下的失效分析［J］.天然气工业，1999，19（4）：77⁃81.

［9］ 王小龙，姚安林.埋地钢管局部悬空的挠度和内力分析［J］.工程力学，2008，25（8）：218⁃222.

［10］ 康习锋，张宏.基于ANSYS的管道屈曲临界载荷分析［J］.油气储运，2017，36（3）：262⁃266.

［11］ 单克，帅健，张思弘.基于修正因子的油气管道失效概率评估［J］.中国安全科学学报，2016，26（1）：87⁃93.

［12］ 朱原池，吴玉国.基于有限元分析的冻土区埋地腐蚀管道力学行为研究［J］.辽宁石油化工大学学报，2019，39（5）：65⁃72.

［13］ 吴玉良，徐国瀚，王国付，等.滑坡灾害中埋地管道稳定性分析［J］.中国安全生产科学技术，2018，14（12）：73⁃77.

［14］ 袁巍华，吴玉国，王国付，等.水毁灾害中埋地管道稳定性研究［J］.中国安全生产科学技术，2017，13（9）：90⁃95.

［15］ 冉龙飞，高文浩，吴栋.埋地悬空管道的应力分析及计算［J］.焊管，2014，37（11）：64⁃67.

［16］ 郭健，李自力，李杨，等.基于ANSYS的埋地套管力学分析［J］.石油化工高等学校学报，2019，32（2）：77⁃83.

Stability Analysis of Suspended Pipeline Based on Finite Element Method

Wang Chao， Li Xiaoling， Wu Yuguo

（College of Petroleum Engineering，Liaoning Petrochemical University，Fushun Liaoning 113001，China）

Soil collapse in natural disasters seriously threatens to the stability of buried pipelines. In order to study the stability of buried pipelines in the suspended collapse area, based on the finite element method,the displacement, strain and stress of buried elbows with different wall thickness and outer diameter in the suspended state were studied. Based on the eigenvalue buckling theory, the ultimate length that the buried elbow can withstand when the soil collapses under certain conditions was studied. The results show that reducing the buried depth, increasing the outer diameter and wall thickness can effectively reduce the displacement of pipeline in soil collapse. The stress and strain of the pipeline occur in the center of the collapse area and the fixed ends of the two sides; the increase of the outer diameter and wall thickness of the pipeline can inhibit the occurrence of local excessive stress to a certain extent. The ultimate length of the buried elbow in the goaf is about 87 m, and improving the outer diameter and wall thickness of the pipeline can enhance the buckling resistance of the buried elbow in the process of soil collapse.

Soil collapse； Buried elbow； Finite element； Buckling eigenvalue

TE83；X937

A

10.3969/j.issn.1672⁃6952.2022.01.009

1672⁃6952（2022）01⁃0047⁃06

2021⁃03⁃09

2021⁃03⁃29

辽宁省博士科研启动基金计划项目（2020⁃BS⁃227）；辽宁省自然科学基金指导计划项目（2019⁃ZD⁃0060）；辽宁省高等学校创新人才支持计划项目（LR2020068）。

王超（1995⁃），男，硕士研究生，从事油气储运技术方面的研究；E⁃mail：982110244@qq.com。

吴玉国（1977⁃），男，博士，教授，从事油气储运技术方面的研究；E⁃mail：wyg0413@126.com。

http：//journal.lnpu.edu.cn

（编辑 宋锦玉）