Sensitivity analysis of Biome-BGCMuSo for gross and net primary productivity of typical forests in China

Hongge Ren ,Li Zhng ,Min Yn,＊ ,Xin Tin ,Xingbo Zheng

a Key Laboratory of Digital Earth Science,Aerospace Information Research Institute,Chinese Academy of Sciences,Beijing,100094,China

b University of Chinese Academy of Sciences,Beijing,100049,China

c Institute of Forest Resource Information Techniques,Chinese Academy of Forestry,Beijing,100091,China

d Key Laboratory of Forest Ecology and Management,Institute of Applied Ecology,Chinese Academy of Sciences,Shenyang,110016,China

e Research Station of Changbai Mountain Forest Ecosystems,Chinese Academy of Sciences,Antu,133613,Jilin,China

Keywords:Sensitivity analysis Biome-BGCMuSo Productivity Regression analysis EFAST

ABSTRACT Background: Process-based models are widely used to simulate forest productivity,but complex parameterization and calibration challenge the application and development of these models.Sensitivity analysis of numerous parameters is an essential step in model calibration and carbon flux simulation.However,parameters are not dependent on each other,and the results of sensitivity analysis usually vary due to different forest types and regions.Hence,global and representative sensitivity analysis would provide reliable information for simple calibration.Methods:To determine the contributions of input parameters to gross primary productivity(GPP)and net primary productivity (NPP),regression analysis and extended Fourier amplitude sensitivity testing (EFAST) were conducted for Biome-BGCMuSo to calculate the sensitivity index of the parameters at four observation sites under climate gradient from ChinaFLUX.Results: Generally,GPP and NPP were highly sensitive to C:Nleaf (C:N of leaves), Wint (canopy water interception coefficient), k (canopy light extinction coefficient),FLNR (fraction of leaf N in Rubisco),MRpern (coefficient of linear relationship between tissue N and maintenance respiration),VPDf (vapor pressure deficit complete conductance reduction),and SLA1 (canopy average specific leaf area in phenological phase 1) at all observation sites.Various sensitive parameters occurred at four observation sites within different climate zones.GPP and NPP were particularly sensitive to FLNR,SLA1 and Wint,and C:Nleaf in temperate,alpine and subtropical zones,respectively.Conclusions: The results indicated that sensitivity parameters of China's forest ecosystems change with climate gradient.We found that parameter calibration should be performed according to plant functional type(PFT),and more attention needs to be paid to the differences in climate and environment.These findings contribute to determining the target parameters in field experiments and model calibration.

1.Introduction

Forests can remove approximately one quarter of the carbon dioxide emitted by fossil fuels and industry,becoming one of the most important nature-based solutions to climate change(Seidl et al.,2017;FAO,2020;Cook-Patton et al.,2020).Accurate simulation of forest carbon fluxes,for example,gross primary productivity(GPP)and net primary productivity(NPP),is an important element of the terrestrial ecosystem carbon cycle and global climate change research.Process-based simulation (PBS)models (e.g.,Biome-BGCMuSo,Community Land Model) take atmosphere-vegetation-soil as a continuous and dynamic system to establish material and energy exchange modules (Pan et al.,2014;Sun et al.,2017) and can describe the main processes of forest ecosystems(e.g.,carbon,nitrogen,and water flux dynamics).Recently,the development of PBS models has provided potential opportunities in terms of terrestrial ecosystem carbon and water cycles and their responses to global climate change (Zaehle et al.,2005;Wang et al.,2011;Li et al.,2020).The running of PBS models relies on conventional ground data,including climatology,meteorology,and vegetation ecophysiological parameters,which results in uncertainties in model outputs due to insufficient prior knowledge of site-specific input parameters (Zhou et al.,2021).Therefore,model calibration by identifying the most influential parameters is necessary for the accurate simulation of carbon and water fluxes.

Sensitivity analysis quantifies how changes in model outputs are attributed to variations in input parameters,and it is widely used in uncertainty assessment,model calibration and diagnostic evaluation and leading control analysis of PBS models (Pianosi et al.,2016).Raj et al.(2014) performed variance-based sensitivity analysis for NPP and GPP from the Biome-BGC model in Douglas-fir forests,and the findings demonstrated that GPP and NPP were particularly sensitive to the C:N of fine roots and leaves related to the development of the leaf area index.Miyauchi et al.(2019)estimated the carbon density of biomass pools inEucommia ulmoidesplantations on the Loess Plateau and believed that the allocation parameters,along with specific leaf area(SLA)and maximum stomatal conductance,strongly affected aboveground woody and leaf carbon density in a sensitivity analysis.Dagon et al.(2020)developed a machine learning method to proceed with the sensitivity and uncertainty of the community land model parameters,which provided an effective framework in model calibration.The results of site-level sensitivity analysis may not be transferable to other regions owing to the climate,soil,and vegetation types.Comprehensive sensitivity analysis of multiple sites and various methods from PBS models are indispensable to understand the expressions of sensitive parameters among vegetation function types and regions.

Biome-BGCMuSo is a newly developed PBS model from Biome-BGC to simulate carbon,nitrogen,and water fluxes,which improves the phenology,multilayer soil,and management modules(Hidy et al.,2016,2021).It requires about 82 ecophysiological parameters to characterize the vegetation processes at the site and over large areas.White et al.(2000) performed parameterization and sensitivity analysis on most ecophysiological parameters of BIOME-BGC,and the results provide a valuable reference for the parameterization and calibration of the model(Turner et al.,2005;Shields and Tague,2015;Miyauchi et al.,2019;Neumann et al.,2020).However,the results ignored the parameter differences in different climate zones and mainly analyzed PFT variability.In addition,with the improvement of the model,the influence of module coupling on the parameters is unknown.Previous studies suggested that sensitivity analysis results may vary according to specific species and regions (White et al.,2000;Tatarinov and Cienciala,2006;Raj et al.,2014;Miyauchi et al.,2019).This may even influence the calibration procedure of Biome-BGCMuSo for specific species under different environmental and site conditions.

In this paper,we applied regression analysis and extended Fourier amplitude sensitivity testing(EFAST)to identify the sensitive parameters of the Biome-BGCMuSo model for GPP and NPP at four sites in China.Our goals are to determine the sensitivity index of input parameters for GPP and NPP and to use this knowledge to gain insight into the capability of the Biome-BGCMuSo model.We aimed to solve the following questions:(1)What are the sensitive parameters for GPP and NPP of different plant functional types (PFTs) in China? (2) How does the response of forest productivity to sensitive parameters change with environmental gradients?This would provide us with informative parameters for further calibration steps and could be extended to the regional scale.

2.Materials and methods

2.1.Observation sites

Four observation sites were selected in this study from ChinaFLUX(Yu et al.,2006,2016),including Changbaishan forest site (CBS),Eddy covariance(EC)observation system ofPotentilla fruticoseL.sample plot in Haibei grassland site (HB),Qianyanzhou forest site (QYZ) and Dinghushan forest site (DHS).These sites are distributed in Jilin,Qinghai,Jiangxi and Guangdong Province in China,covering a large range of latitudes(between 42°N and 21°N),climate zones from North to South China(Fig.1).Moreover,these sites represent different temperature and water gradients in China,covering different forest PFTs ranging from needle forest and deciduous broad-leaved forests (DBF) in the north to evergreen broad-leaved forest(EBF)and evergreen needle-leaved forests(ENF)in the south as well as shrubs in the alpine climate zone on the edge of the Qinghai-Tibetan Plateau.The details of each site were shown in Table 1.

Table 1 Site descriptions.

Eddy covariance (EC) systems were used to assess the accuracy of Biome-BGCMuSo in simulating GPP and NPP.The observation sites use an open-circuit vorticity correlation system to carry out flux observations and simultaneous gradient observations of conventional meteorological elements.From the ChinaFLUX data,we obtained daily gross ecosystem exchange (GEE) and net ecosystem exchange (NEE) during the 2003-2010 period for the eddy covariance(EC)-based carbon flux towers at the four observation sites (Dai et al.,2020;Wu et al.,2020;Zhang et al.,2020;Li et al.,2021).The acquired data are based on the China-FLUX technology system to complete standardized quality control and data processing (Yu et al.,2014).The daily GPP and NPP values were calculated by inverse operation of GEE and NEE.

2.2.Biome-BGCMuSo model

For this work,we used the latest version of Biome-BGCMuSo(V6.1),which was released by the research group of Prof.Zoltán Barcza at the Meteorology Department of Eötvös Lorand University(Hidy et al.,2021).Compared to Biome-BGC,Biome-BGCMuSo is mainly characterized by a multilayer soil module,drought-related plant senescence module,phenology module,and management module (e.g.,cropland mowing,grazing,fertilization,harvest and forest thinning).Biome-BGCMuSo also introduced new input variables(for example,measured drain coefficient,hydraulic coefficient,ratio of dry matter and carbon content) and new output parameter variables(cumulative evaporation and transpiration).

The carbon flux module,phenology module and soil flux module are the three most important modules in Biome-BGCMuSo.In the carbon flux module,the photosynthesis program of Farquhar(1980)and the enzyme kinetic model based on Woodrow and Berry(1988)are used to calculate the GPP of the biological community.Autotrophic respiration is divided into maintenance respiration and growth respiration.In addition to temperature,maintenance respiration is a function of the N content of living plant pools,and growth respiration is a fixed ratio of GPP (Hidy et al.,2016).The phenological module calculates foliage development.There are two models in the phenology module:the optional HSGSI method described in Hidy et al.(2012) and the original Biome-BGC model logic.In this study,we chose the original Biome-BGC model logic since our ecosystem type is forest.The soil flux module describes the decomposition of dead plant material and soil carbon pools.There are three significant developments of the soil flux module in the current model version:standing dead biomass and harvested biomass pools and a ten-layer soil sub-model.

Biome-BGCMuSo uses at least four input files when it is executed:initialization file (INI file),meteorological data file (MET file),soil property file (SOIL file),and a file for ecophysiological constants (EPC file) (Hidy et al.,2021).We elaborated the input files according to the particularity of the observation sites.For the INI file,CO2and nitrogen deposition are mainly set.The MET file includes the daily values of maximum and minimum air temperatures,precipitation,solar radiation,and vapor pressure deficit.In the SOIL file,we mainly set the soil texture parameters.The EPC file needs to be parameterized according to different PFTs.The detailed data sources and parameterization scheme are described in Section 2.3.

The model simulation is divided into two stages.The first is spinup simulation,which starts with very low initial levels of soil C and N and runs until it reaches a steady state under a given climate to estimate the initial values of state variables(Thornton and Rosenbloom,2005).Next is the normal simulation,which uses the spinup simulations as the initial values of the C and N pools,and the simulation is performed within a predetermined period.Therefore,it is necessary to obtain a long-term series of daily data to drive the whole simulation.In this study,each simulation ran for 36 years from 1975 to 2010,with the first 28 years used as spin-up to bring the model into equilibrium and the last 8 years used for normal running.

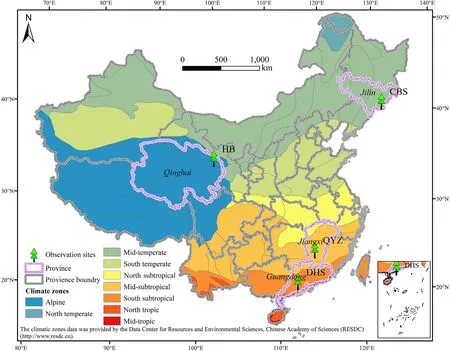
Fig.1.Observation sites and climate zones.

2.3.Input data and parameterization

CO2concentration data were derived from the Mauna Loa CO2dataset and historical CO2dataset(htp://www.co2.earth).N deposition was provided by ChinaFLUX (http://rs.cern.ac.cn).The soil texture dataset was provided by the Data Center for Resources and Environmental Sciences,Chinese Academy of Sciences (RESDC) (http://www.resdc.cn).The soil texture data were compiled based on the 1:1 million soil type map and the soil profile data obtained from the second soil survey in China.The soil texture was classified according to the percentage of sand,silt,and clay.

Meteorological data included daily minimum and maximum temperatures,the average daily air temperature,daily precipitation,daily average global radiation,and daily average water vapor pressure difference(VPD).First,we obtained the daily minimum temperature,daily maximum temperature and daily precipitation data from 1982 to 2003 for the four meteorological stations named Changbai(128°11′E,41°25′N),Jiuji(101°29′E,33°26′N),Xunwu(115°39′E,24°57′N),and Fogang(113°32′E,23°52′N) from the China Meteorological Data Network(http://data.cma.cn).These four meteorological stations are close to CBS,HB,QYZ,and DHS.Then,the meteorological station data were converted into the model input meteorological data of the corresponding flux station in the MT-CLIM 4.3 program for the spinup simulation.Finally,the model input meteorological data from 2003 to 2010 were obtained from ChinaFLUX and used for the normal simulation.

A total of 48 parameters in the EPC input file were selected to fluctuate within specific ranges according to the literature.First,basic values were determined by measurements and literature.Then,the variation range of each selected parameter fluctuated by 20%(White et al.,2000).Because of the individual biochemical and physical constraints,the maximum and minimum values of some parameters constitute the variation ranges.Table 2 shows the candidate input parameters selected in this study and their description information.The basic values and their source information of input parameters for CBS,HB,QYZ and DHS are shown in the Supplementary.

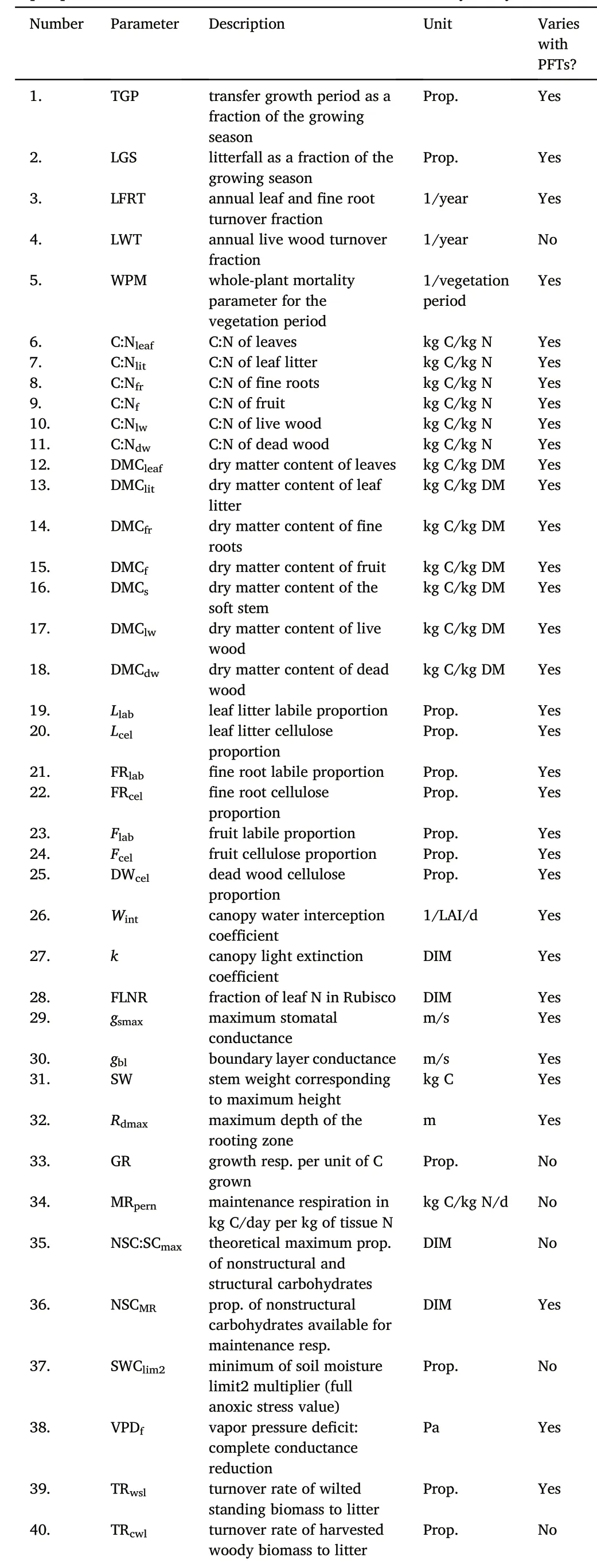
Table 2 Input parameters of Biome-BGCMuSo used in the sensitivity analysis.

Table 2 (continued)

2.4.Sensitivity analysis

Regression analysis and EFAST were adapted for the sensitivity analysis of Biome-BGCMuSo,and the contributions of the input parameters to GPP and NPP were quantified.Details of the regression analysis and EFAST methods are provided in subsequent sections.

2.4.1.Sensitivity analysis based on regression analysis

The basic idea of regression sensitivity analysis is to obtain information about output sensitivity from the statistical analysis of the input data set generated by Monte Carlo simulation(Zagayevskiy and Deutsch,2015).Regression analysis derives the sensitivity measure as a parameter of the regression analysis applied to the input/output sample set (Hosman et al.,2010;Richard and Christopher,2020).Here,the multiple linear regression method was used to obtain the sensitivity to all single input factors at once.Since the input parameters have different units,the standard regression coefficient is used.The linear least squares estimation of regression coefficients is a measure of sensitivity,and the formula is expressed as

where SIiis the sensitivity of thei-th input parameter,biis the regression coefficient,SD（Xi）is the standard deviation of multiple sampling of theith input parameter,and SD（Y）is the standard deviation of the model's corresponding outputY(NPP and GPP).

2.4.2.Variance-based sensitivity analysis:EFAST

EFAST is a global sensitivity analysis algorithm that quantifies the sensitivity of a single parameter and multiple parameters to the outputs(Saltelli,2002).It is widely used in the sensitivity analysis of nonlinear models,such as Biome-BGC (Yan et al.,2016),crop growth models(Vazquez-Cruz et al.,2014),and building energy models (Nguyen and Reiter,2015).Each input parameterXihas a range of random variables that results in the distribution of an output simulatorY,which can be represented mathematically as

whereYis the output (NPP and GPP) of Biome-BGCMuSo.Xrepresents the set of input parameters,andXiis the input parameter with a given upper and lower floating boundary.

EFAST indicates that the variance of the model output can adequately express the uncertainty of the parameter variations in the model results,as shown in equations(3)-(6):

whereVYis the total variance of the model output,andViis the variance of the conditional expectation(VCE)ofYgiven that thei-th inputXihas a fixed valueis the VCE ofYgiven that thei-th inputXihas a fixed valueand thej-th inputXjhas a fixed valueVijkis the VCE ofYgiven that the inputsXi,Xj,andXkhave fixed values of,andrespectively.

Sensitivity is measured by the contribution of a given input factor to the output variance (Pianosi et al.,2016).In this study,we selected the first-order sensitivity index (Si) and the total sensitivity index (SiT) to quantify the contributions of the input parameters to the outputs.

The first-order sensitivity index(Si)measures the direct contribution of each input factor to the output variance or the expected reduction in output variance when a specific input is fixed (Saltelli,2002).It can be represented mathematically as

The total sensitivity index(SiT)can be represented mathematically as

In this study,48 input parameters of Biome-BGCMuSo were evaluated by computing SIi,SiandSiTfor the GPP and NPP model outputs.First,according to the range of each input parameter(see Supplementary),the Monte Carlo method was used to uniformly sample each parameter.In this study,the sampling frequency was 4800(48 ×100) for each forest PFT.Since CBS and DHS are mixed forests,the total sampling frequency of different PFTs at the 4 observation sites was 28800 (6 × 4800).According to the generated multiple sets of input parameters,we ran the Biome-BGCMuSo model in batches.GPP and NPP at the observation site from 2003 to 2010 were simulated for the normal stage.Second,the average GPP and NPP were calculated as the final model outputs.The sensitivity results using regression analysis and EFAST were analyzed in the RBBGCMuSo-master R package and SimLab 2.2.Finally,the sensitivity index (SIi,SiandSiT) was divided into two groups.When the sensitivity index is greater than 0.1,the corresponding parameter is the sensitive parameter;otherwise,the parameter is not the sensitive parameter.In addition,the key sensitivity parameter refers to the corresponding parameter when SIiandSiTare both greater than 0.1.

3.Results

3.1.Uncertainty in simulated GPP and NPP

The uncertainty of GPP and NPP from the input data was calculated using EFAST.Fig.2 shows the distribution of GPP.Generally,the GPP value of subtropical forests(QYZ and DHS sites)was higher than that of other forest sites.The GPP distribution of shrubs was relatively scattered,while that of ENF was relatively concentrated.QYZ with planted ENF and DHS with EBF had obvious discrete values.Table 3 shows the descriptive statistics including minimum values (min),maximum values (max),mean values (mean),standard deviation (SD),and coefficient of variations (CV) of the annual average GPP for forest PFTs at the observation sites.The uncertainty (coefficient of variation,CV) of GPP in DBF was greater than that in ENF.The CV of DBF at CBS was 39%,with a range of 168-1383 g C•m-2•year-1for GPP.The uncertainty of ENF at CBS was 9%,with a range of 1417-2641 g C•m-2•year-1for GPP.The uncertainty of GPP in planted forests was higher than that in natural forests,and the CVs of ENF at QYZ and DHS were 11%and 4%,respectively.In general,the uncertainty of temperate forest sites was higher than that in other climatic zones.

As shown in Fig.3,ENF at the CBS site had the highest NPP.The QYZ forest site with planted ENF had the most discrete NPP.The highest NPP uncertainty occurred in the DBF type (with CV=41%),which was similar to GPP(Tables 3 and 4).

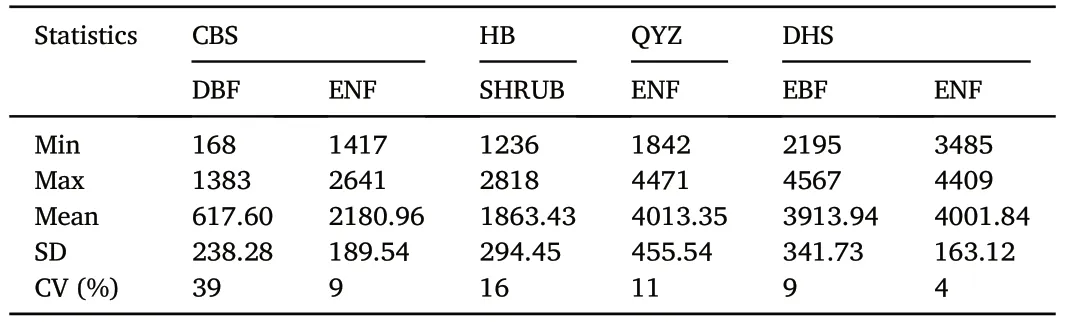
Table 3 Min,max,mean values,standard deviation(SD)and coefficient of variation(CV)of the annual average GPP for forest PFTs at the observation sites.

Table 4 Min,max,mean values,standard deviation(SD)and coefficient of variation(CV)of the annual average NPP for forest PFTs at the observation sites.

Both GPP and NPP for ENF at the QYZ forest site had obvious discrete values.The amounts of GPP and NPP distributed in the ranges of 1842-3200 and 200-400 g C•m-2•year-1were zero,respectively.These findings illustrated that under certain parameter combinations,forests experience unsustainable or disturbed growth during years of model simulation.However,the sensitivity analysis was not affected by the above conditions due to the available and useful spinup phase,and it also explained that the sensitive parameters led to the scattered distribution of GPP and NPP values.

3.2.Sensitivity analysis of GPP and NPP based on regression analysis

As mentioned in 2.4.2,sensitive parameters were those with SIigreater than 0.1.The left and right sides of Fig.4 show the sensitive parameters of GPP and NPP calculated by regression analysis.

Overall,both GPP and NPP were sensitive to 8 parameters:C:Nleaf,Wint,k,FLNR,GR,MRpern,VPDf,and SLA1.Specifically,MRpernwas the parameter with maximum sensitivity for ENF and EBF types,especially in subtropical climate zones.At the shrub site,both GPP and NPP were sensitive toWintand SLA1,which was completely different from the other forest sites.Notably,one major difference in the sensitive parameters between GPP and NPP was C:Nfr,that is,NPPs for all observation sites were not sensitive to C:Nfr.

The sensitive parameters varied with different climatic zones.In temperate zone(CBS site),FLNR was the common sensitive parameter for DBF and ENF,with respective SIivalues of 16% and 29% for GPP and 14%and 31%for NPP.In the alpine zone(HB site),GPP and NPP were severely restricted byWint.This may be becauseWintcontrols the percentage of precipitation that enters the soil water pool and that is transpired,while HB had the lowest precipitation among the four observation sites,andWintin turn became the main limiting factor in those waterstressed regions.In the subtropical zone (QYZ and DHS sites),different PFTs also showed similar sensitive parameter combinations.C:Nleafexerted a significant control on GPP and NPP for all PFTs except the most sensitive parameter MRpern.C:Nleafdirectly affects the distribution of carbon and nitrogen in leaves and then affects photosynthesis and cumulative productivity.

Fig.2.The distribution of the annual average GPP for forest PFTs at the observation sites.

For different PFTs,individual parameters had a large impact on specific PFTs.Shrubs were most sensitive toWint(GPP:38%;NPP:39%)and SLA1(GPP:32%;NPP:31%).For the evergreen types(ENF and EBF),MRpernwas the most sensitive parameter,which mainly controlled plant growth.For DBF,VPDfexhibited very high sensitivity,with both 50%for GPP and NPP.

3.3.EFAST for GPP and NPP

The first-order sensitivity index(Si)and total sensitivity index(SiT)of the selected parameters for GPP and NPP at the four observation sites are shown in Figs.5 and 6.Sensitive parameters were shown above the red(in the Web image)dashed line.

As shown in Figs.5 and 6,SiandSiTof VPDf,Wint,SLA1,andkwere similar for GPP and NPP,which controlled GPP and NPP either directly or through interaction.FLNR was the common sensitive parameter in the temperate zone(CBS site).DBF and ENF at CBS site were most influenced by VPDfandWint,respectively.For the unique shrub site,SLA1 was the most sensitive parameter for GPP.kdisplayed the highestSiandSiTin subtropical zones (QYZ and DHS sites).MRpernexerted a significant control on NPP for all PFTs except shrubs.More sensitive parameters appeared in the total sensitivity index than those inSifor the QYZ and DHS sites.This indicated that numerous parameters strongly influenced GPP only through interactions.

3.4.Comparison and analysis of the results for the two sensitivity analysis methods

Seven key sensitive parameters for GPP and NPP were summarized from the two sensitivity analysis methods:C:Nleaf,Wint,k,FLNR,MRpern,VPDf,and SLA1 (Figs.7 and 8).The sensitive parameters selected by regression analysis were similar to those from EFAST,and the key sensitive parameters differed significantly under various climate environments and PFTs.FLNR was the key sensitive parameter in temperate zone,and C:Nleafwas the key sensitive parameter in subtropical zones.VPDfwas the key sensitive parameter for DBF,and GR was the key sensitive parameter for ENF at the CBS site.At the DHS site,C:Nleafandkwere the key sensitive parameters of EBF,and C:Nfrwas the key sensitivity parameter of ENF.In addition,C:Nfrwas the sensitive parameter only for ENF-type GPP at the DHS site,while GR was the sensitive parameter only for ENF-type NPP at the CBS site.

4.Discussion

4.1.A framework for optimizing forest primary productivity parameters based on sensitivity analysis

The key sensitive parameters extracted according to different sensitivity analysis methods have a high degree of similarity.It is therefore necessary to perform a series of steps for key sensitivity parameters to simplify the process from sensitivity analysis to parameter correction.Here,we refer to these steps as the“workflow”.The workflow for the application of key parameters is shown in Fig.9.The colored parameters should be of importance in sensitivity analysis and modeling.We described and discussed the workflow and the choices that the user must make in each step to provide practical guidelines to support the user in the sensitivity analysis-based simulation correction of the parameters.

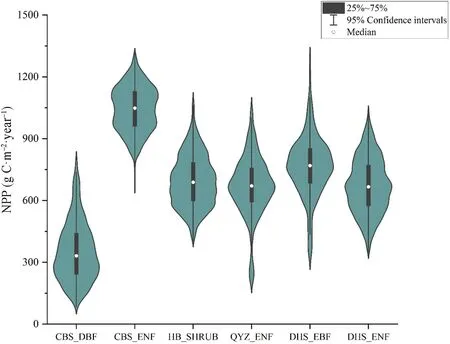
Fig.3.The frequency distribution histogram of the annual average NPP for forest PFTs at the observation sites.

The most important thing in the experimental design of sensitivity analysis is to determine the parameters and sensitivity analysis methods.These together constitute what we call the“experimental settings.”Specifically,the chosen parameters include(i)selecting the input factors to be accepted by the sensitivity analysis and their floating intervals and(ii)setting the values of other input factors,and these input factors will remain constant throughout the sensitivity analysis.The selection of sensitivity analysis methods can be found in the application process of sensitivity analysis proposed by Pianosia et al.(2016).

Fig.4.The SIi of GPP (left) and NPP (right) at the observation sites.

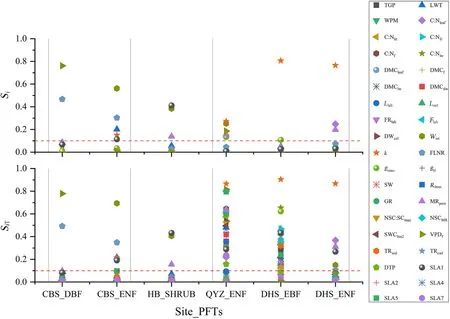
Fig.5.The first-order sensitivity index (Si) and total sensitivity index (SiT) of GPP at the observation sites.

Fig.6.The first-order sensitivity index (Si) and total sensitivity index (SiT) of NPP for forest PFTs at the observation sites.

Fig.7.The key sensitivity parameters of GPP for different forest PFTs at the observation sites.

Fig.8.The key sensitivity parameters of NPP for different forest PFTs at the observation sites.

The results described in sections 3.2 and 3.3 indicate that the sensitivity of the climate environment to productivity simulation is greater than the difference in PFTs.Specifically,the most common sensitivity parameter of different PFTs in the temperate zone was FLNR,followed by MRpern.In the alpine zone,the common sensitive parameters of different PFTs were SLA1 andWint.In addition,C:Nleafwas the key sensitive parameter for different PFTs in the subtropical zone,followed by MRpern.Next was the selection of key sensitive parameters for different PFTs.In the temperate zone,DBF was sensitive to VPDf,and ENF was sensitive to GR.In the subtropical zone,EBF was sensitive tok,and ENF was sensitive to C:Nfr.In addition,GR and C:Nfrwere the key sensitive parameters of NPP and GPP,respectively,excluding the common key sensitive parameters of NPP and GPP.As the importance of the parameters gradually decreases with the deepening of the workflow,the disturbance effect of the following parameters on the simulation results gradually decreases.In the application workflow for key parameters,if some key sensitive parameters (such as GR and C:Nfr) have been added before,the corresponding steps can be omitted in the following process.

The uncertainty discussed in Section 3.1 is intended to assess the uncertainty of the results of a particular sensitivity analysis method,therefore providing information on the reliability of the results within the scope of the method.A different and equally relevant question is the degree to which the method itself can be trusted,that is,whether the method is suitable for solving the expected answer when applied to the immediate question.For example,variance-based sensitivity analysis methods rely on the assumption that variance is a wise substitute for uncertainty and may not be correct for highly skewed output distributions.In this case,even if researchers can obtain an almost completely accurate estimate of the sensitivity index based on variance,they cannot provide a correct ranking (Liu et al.,2005).Therefore,the sensitivity analysis results may be very reliable,but they still need to be based on actual conditions.Circumstances evaluate the accuracy of the results and explain the reasonableness of the sensitivity analysis results.

Fig.9.A framework for optimizing forest primary productivity parameters based on sensitivity analysis.

4.2.Uncertainty of the input parameters

The use of the input parameter values of a specific site can achieve the best simulation and a relatively high degree of acceptance of the sensitivity analysis results (Thornton et al.,2002;Toriyama et al.,2021).There are two main limitations:(1) Some input parameters cannot be directly observed,such as FLNR and parameters related to decomposition and distribution (Llab,Lcel).(2) The variation range of parameters is difficult to obtain.In this study,the main parameters related to C and N allocation,plant height,and root depth were obtained from actual measurements or research at the observation sites.Parameter localization was carried out based on the model default parameters (see Supplementary).

To explore the impacts of different basic values of the parameters on outputs,we analyzed the simulated GPP of the CBS site under three schemes:(1) default parameters;(2) localized parameters;and (3) corrected parameters based on sensitivity analysis.The results were validated against EC flux tower measured values,as shown in Fig.10.Rows(a),(b)and(c)represent different PFTs of the mixed forest,DBF and ENF,respectively.The results show that the model calibrated by sensitivity analysis had the best simulation compared with EC flux tower measured values,especially for ENF,withR2=0.69,which improved by 16%and 10%compared to schemes 1 and 2.The sensitive parameters control the key processes associated with the GPP simulation.By correcting related sensitive parameters,the uncertainty of input parameters can be effectively reduced,and the simulation accuracy of the process model can be improved.

Previous studies showed that parameters with smaller basic values were more susceptible to the influence of the parameter range,and a narrow range would limit the sensitivity index of a small parameter(Ma et al.,2020).Therefore,the range of the parameter is crucial to the result of the sensitivity analysis.In this study,under the premise of giving priority to physical or biological constraints,the localized parameters are all taken as the parameter perturbation range with fluctuations of 20%(White et al.,2000).The consistency of the parameter range is guaranteed to a certain extent.

4.3.Sensitive parameters

According to recent studies,it was predicted that forest carbon sequestration decreased with increasing carbon dioxide and would possibly be a carbon source in the future(Cox et al.,2000;Baccini et al.,2017;Brienen et al.,2020).In contrast,some studies demonstrated that the absorption capacity of forest carbon sinks would continue (Wang et al.,2020;Harris et al.,2021;Heinrich et al.,2021).This means that considerable uncertainties exist during carbon flux simulation and even the climate-forest carbon cycle feedback mechanism.Therefore,sensitivity analysis was applied in this study,aiming to distinguish the model's influential parameters and examine carbon flux output sensitivity.

Our results showed that 7 parameters had important impacts on both GPP and NPP.However,many parameters in BIOME-BGCMuSo exhibited extremely low sensitivity for GPP and NPP,for example,LGS(litterfall as a fraction of the growing season),LWT (annual live wood turnover fraction),and parameters related to the dry matter content(DMClit(dry matter content of leaf litter),DMCf(dry matter content of fruit),and DMCdw(dry matter content of dead wood)).The parameters that most influenced GPP and NPP were those controlling respiration and the assimilation rate of photosynthesis,such as MRpern,FLNR,and C:Nleaf.This result is consistent with the results from White(2000),Raj(2014),and Dagon (2020).MRpernrepresents the coefficient of linear relationship between tissue N and maintenance respiration,which is directly related to maintenance respiration and further affects GPP and NPP(Ryan,1991).FLNR controls the potential rate of carboxylation and directly affects VCmax;therefore,it is a dominant control of canopy assimilation (Stitt and Schulze,1994;White et al.,2000).C:Nleafis a compound parameter that determines the important factors of the nitrogen required to construct leaves,the amount of nitrogen available for investment in photosynthetic machinery,and leaf respiration rates.

The sensitive parameters varied under different climate and environmental conditions.FLNR had a strong influence on GPP and NPP in the temperate zone;C:Nleafwas sensitive in the subtropical zone.This indicated the limiting effects of light,water,temperature and mineral nutrients on primary productivity under different climatic environments in previous studies(Knapp et al.,2014).In addition,many studies have shown that leaf traits change significantly along temperature and rainfall gradients (Domínguez et al.,2012;Wright et al.,2017).As the latitude increases,Rubisco activity is significantly inhibited,which affects FLNR and inhibits the assimilation of C.In contrast,the temperature weakly restricts the activity of Rubisco in subtropical areas.This may explain why FLNR has high sensitivity in the temperate zone.C:Nleafis directly related to the nitrogen content in the leaves.The nitrogen content directly affects the content of chlorophyll,thereby affecting photosynthesis.Gong et al.(2020)investigated the leaf traits of different life forms at different latitudes in northeastern China and found that nitrogen was limited in low latitude areas and that leaf traits were very sensitive to climate factors.Our results clarify the key sensitivity parameters of GPP and NPP in different climatic environments and provide information for the accurate simulation and parameter correction of GPP and NPP at regional scale.

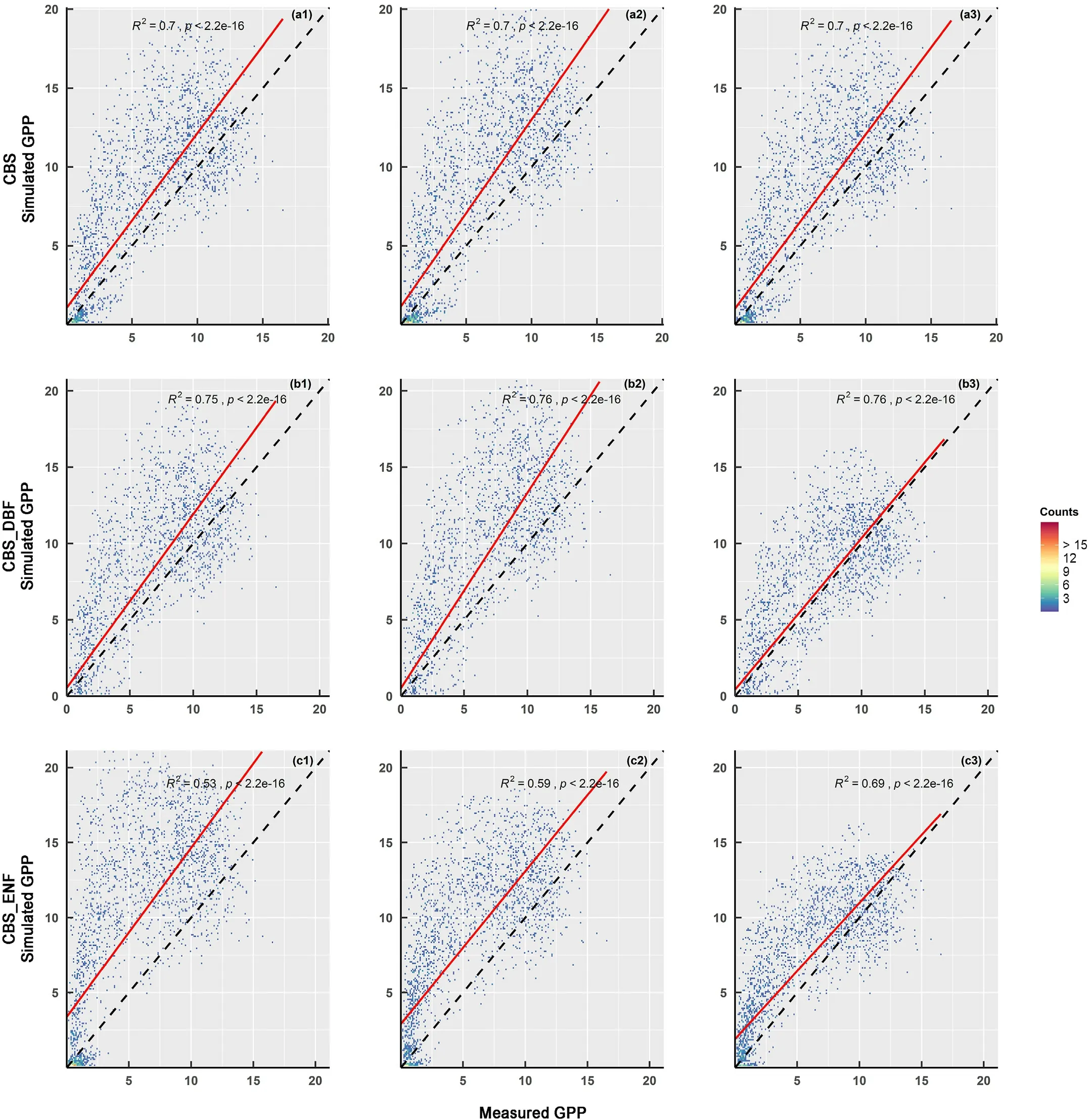
Fig.10.Comparison of the correlation between simulated GPP under default(a1,b1,c1),localized(a2,b2,c2),corrected(a3,b3,c3)schemes and eddy covariance(EC) flux tower measured values at the CBS site.

5.Conclusions

Two sensitivity analysis methods,regression analysis and EFAST,were used in this work to determine the key parameters of the Biome-BGCMuSo model.The key sensitivity parameters extracted according to different sensitivity analysis methods had a high degree of similarity.The results demonstrated that C:Nleaf,Wint,k,FLNR,MRpern,VPDf,and SLA1 were the most sensitive parameters for GPP and NPP.Specifically,GPP and NPP were most sensitive to FLNR,SLA1 andWint,and C:Nleafin temperate,alpine and subtropical zones,respectively.Finally,we suggested a framework of sensitivity analysis by considering different climate conditions,which would present a reliable solution of decreasing the complexity of calibrating process-based models.We emphasize that the calibration of parameters should be based on PFTs,and more attention should be paid to the differences in climate and environment.

Ethics approval and consent to participate

Not applicable.

Consent for publication

Not applicable.

Availability of data and materials

The datasets used or analyzed during the current study are available from the corresponding author on reasonable request.

Declaration of competing interest

The authors declare that they have no competing interests.

Funding

This study was funded by the National Natural Science Foundation of China(grant number 41871279 and 41901364).

Authors' contributions

Hongge Ren and Li Zhang devised the main theoretical framework and proof outline.Hongge Ren performed the analytic calculations and model simulations and took the lead in writing the manuscript.Min Yan and Xin Tian provided significant feedback and helped shape the research,analysis and manuscript.Xingbo Zheng provided some of the climate data for the research.All authors read and approved the final manuscript.

Acknowledgments

Biome-BGCMuSo was developed from the widely used Biome-BGC model that was created by the Numerical Terradynamic Simulation Group (NTSG),University of Montana.We thank all the scientists,software engineers,and administrators who contributed to the development of Biome-BGC and Biome-BGCMuSo 6.1.We thank ChinaFLUX for providing long-term monitoring data of the forest ecosystem at the observation sites,such as phenology,plant community composition,mineral element content and energy of dominant plants and litter of the forest plant community.

Abbreviations

GPP Gross primary productivity

NPP Net primary productivity

PFTs Plant functional types

PBS Process-based simulation

CBS Changbaishan site

HB Haibei site

QYZ Qianyanzhou site

DHS Dinghushan site

DBF Deciduous broad-leaved forests

ENF Evergreen needle-leaved forests

EBF Evergreen broad-leaved forests

GEE Gross ecosystem exchange

NEE Net ecosystem exchange

INI file Initialization file

MET file Meteorological data file

SOIL file Soil property file

EPC file File for ecophysiological constants

Prop.Proportion

DIM Dimensionless

DM Dry matter

VCE Variance of the conditional expectation

SD Standard deviation

CV Coefficient of variation

VCmax Maximum carboxylation rate

Note:The abbreviated representation and description of the model input parameters are shown in Table 2.

Appendix A.Supplementary data

Supplementary data to this article can be found online at https://do i.org/10.1016/j.fecs.2022.100011.