数学模型思想渗透的教学与思考

【摘 要】以苏科版数学教材“用一元二次方程解决问题（1）”为例，从模型回顾、模型建构、模型应用、总结提升四个教学环节阐述教学意图，分析教学效能。从对模型思想的再認识、对模型思想渗透的再思考、对培养建模能力的再理解三个维度阐释在初中数学教学中渗透模型思想的策略。

【关键词】初中数学；模型思想；一元二次方程；解决问题

【中图分类号】G633.6  【文献标志码】A  【文章编号】1005-6009（2022）59-0046-04

【作者简介】孙凯，江苏省苏州市阳山实验初级中学校（江苏苏州，215151）教师，高级教师。

模型思想是数学的基本思想之一，数学模型是数学应用的重要形式，数学建模是应用数学知识解决实际问题的基本手段。

在初中阶段，渗透模型思想是培养初中生数学建模能力的主要路径。但在实际教学中，教师对模型思想的认识和理解不够深刻，对模型思想的发掘和渗透不到位，导致学生对数学模型认识模糊、建构模型能力不足。本文以苏科版数学教材九年级上册第一章“用一元二次方程解决问题（1）”为例，谈谈如何在数学教学中渗透建模思想，培养初中生的数学建模能力。

一、教材简析

1.对教材的理解

“用一元二次方程解决问题”是苏科版数学教材九年级上册第一章“一元二次方程”第4节的教学内容，教材在此小节设置了3课时教学内容，每课时编排两个典型问题。本课为第1课时，教材中设置的两个问题分别为“面积问题”和“增长率问题”。两个问题与现实生活紧密联系，符合初中生的认知基础和认知经验，有利于初中生在最近发展区内运用数学知识解决实际问题，使学生在数学建模的过程中体会一元二次方程模型是刻画现实世界的有效模型。

在教学时，教师不应过于侧重实际问题的归类教学，而应淡化对问题的归类，将教学重点聚焦于“类属问题”的本质上——数学模型的建构。这才符合教材编写者的真实意图，也是进行实际问题教学的应有之义。

2.教学目标与解析

【教学目标】经历和体验用一元二次方程解决“增长率问题”和“面积问题”的过程，进一步体会一元二次方程是刻画现实世界数量关系的重要数学模型［1］，增强数学应用意识，培养数学建模能力；会根据具体问题中的数量关系列出一元二次方程并求解，能检验所得的结果是否符合实际意义；经历引模、建模、解模、验模的数学建模过程，进一步提高发现和提出问题、分析和解决实际问题的能力。

【解析】从学生的认知基础看，在“面积问题”中，建立一元二次方程模型是没有障碍的。而在“增长率问题”中，学生的认知经验停留在“一次”增长上，往往对“二次”增长不太理解。因此，教学目标应指向学生经历和体验建构数学模型求解问题的过程，重点是渗透模型思想，帮助学生突破认知障碍，使学生在分析求解实际问题的过程中建构不同的数学模型，培养数学建模能力。

二、教学过程

（一）模型回顾

引问：母亲节期间，鲜花店里的某种鲜花价格上浮了20%，小明花18元买了一束鲜花送给妈妈，求这束鲜花原来的价格。

【教学意图】本环节对教材上的问题顺序进行了调整，先呈现增长率问题，从学生熟悉的“一次”增长问题着手，为“二次”增长的学习奠定基础，有利于学生回顾用方程求解实际问题的一般步骤，唤醒其建构方程模型求解实际问题的认知经验。

【效能分析】学生能理解“引问”中的数量关系，并总结用一元一次方程解决问题的一般步骤——审题、设未知数、找等量关系、列方程、求解、检验、作答。本题使学生初步体会从“起始数”到“终端数”的变化规律，初步感悟一次增长的数学结构特征，为二次增长模型的学习奠定基础。

（二）模型建构

【问题1】某商店6月份的利润是2500元，要使8月份的利润达到3600元，平均每月利润增长的百分率是多少？

【教学意图】问题1属于“二次增长型”增长率问题。在引问的基础上，促进学生迁移认知经验，将“一次增长模型”拓展至“二次增长模型”，建立一元二次方程模型，使学生经历引模、建模、解模、验模的数学建模活动过程，对获得的数学模型进一步抽象、概括，形成“增长率模型”a（1+x）2=b。

【效能分析】学生在“一次”增长的认知基础上获得一元二次方程模型2500（1+x）2=3600。在求解该方程模型时，教师应引导学生思考选用哪种解法比较合理，帮助学生完成求解模型的任务。在此环节，适时渗透模型思想，进一步引导学生将“起始数2500”和“终端数3600”符号化，使学生体会一类实际问题中稳定的数学结构，用数学模型的视角理解实际问题中蕴含的数学本质。

【问题2】在淘宝网上购买了60m的栅栏围成矩形场地。（1）写出围成的矩形场地面积y（m²）与长x（m）之间的关系式；（2）能围成面积为200m²的矩形场地吗？（3）能围成面积为240m²的矩形场地吗？

追问：你能提出一个有关面积的问题吗？

【教学意图】问题2属于“矩形面积”问题。教师可先安排学生画图，引导其从几何直观的视角体会面积问题，感悟数学模型的几何意义。在60m栅栏的实际背景下，设置了3个问题。第一个问题驱动学生获得函数模型y=x（30-x），感悟矩形面积会随长度的变化而变化，为建构一元二次方程模型奠定基础。后两个问题涉及具体的矩形面积，即对面积y赋值，将函数模型转化为方程模型，驱使学生自觉感悟函数（二次函数）与方程（一元二次方程）的内在联系。追问环节预设学生会提出矩形场地面积最大的问题，引导学生运用“配方法”求最值，为后续研究二次函数的图象和性质打下坚实基础。

【效能分析】学生能画出矩形辅助分析问题，写出y=x（30-x）的函数模型，进一步将y更换为200或240，求解一元二次方程，获得数学结果。在追问环节，学生能说出“围成正方形时面积最大”，但面对“为什么围成正方形时面积最大”这一问题，学生往往不能作出合理解释。此时，教师应注重引导学生运用配方法解决最大值问题。

（三）模型应用

【习题】1.某服装原价每件80元，经过两次降价，现售价每件51.2元。求该种服装平均每次降价的百分率。

2.某商品連续两次降价10%后价格为a元，则该商品的原价为（  ）。

A. [a/1.21]元   B. 1.12a元

C. [a/0.81]元   D. 0.81a元

3.一块长方形菜地的面积是150m²。如果它的长减少5m，那么它就成为正方形菜地。求这个长方形菜地的长和宽。

4.学校打算用长16m的篱笆围成一个长方形的生物园饲养小兔，生物园的一面靠墙（如图1），面积是30m²。求生物园的长和宽。

【教学意图】本环节的4个问题分别对应了增长率模型和面积模型。其中题1、题2是对增长率模型的拓展，将“增长”拓展至“降低”，使学生在解决“新问题”的过程中体悟实际问题背后蕴含的数学本质，将数学模型进一步完善为a（1±x）2=b。题3、题4是对面积模型ab=c的实际应用，学生从问题中找到长、宽、周长、面积之间的关系是解决问题的关键。

【效能分析】学生从题1中能正确建立一元二次方程模型，但在求解模型时，部分学生出现求解错误甚至不会求解的现象。题2相对简单，学生能正确建立模型并出示结果。题3教师可引导学生画图分析题意，完成设、列、解、验等步骤。在题4中，学生在建立模型求解出结果后，有很多学生不知道或者不会检验，因而教学中应及时予以强化。

（四）总结提升

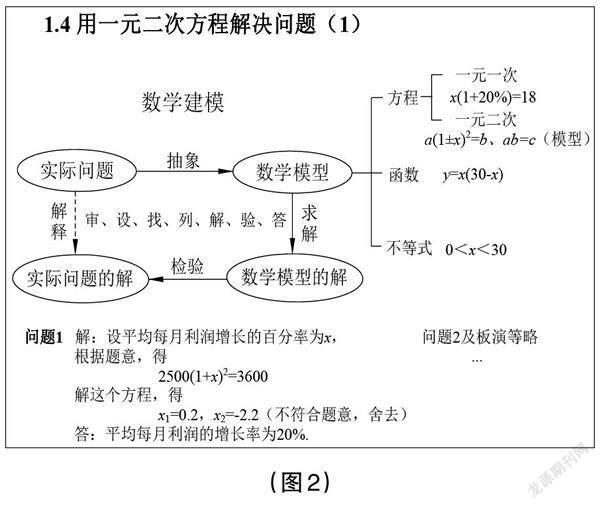
本环节教师安排学生总结学习情况，思考、讨论、交流、提升。（板书见图2）

【教学意图】引导学生从数学建模的视角总结建立一元二次方程解决问题的过程，渗透模型思想，培养数学建模能力。

【效能分析】借助板书设计总结利用一元二次方程解决问题的数学建模过程，帮助学生体悟模型思想。

三、教学思考

1.对模型思想的再认识

史宁中教授指出数学发展所依赖的思想本质上有三个：抽象、推理、模型。其中模型是数学世界连接外部世界的桥梁。［2］

研究《义务教育数学课程标准（2022年版）》不难发现，课标注重在代数式、方程、不等式和函数等“数与代数”领域内容中渗透模型思想，从而帮助学生建立模型观念。因此，在代数式、方程、不等式、函数等数学概念教学中，教师应注重引导学生从实际问题情境中抽象出数学对象，进一步建立数学模型，这是教学的关键环节。就本节课而言，教师设计适切的实际问题，引导学生建立一元二次方程模型，体会模型思想是教学的核心。因此，在初中学段数学教学尤其是解决实际问题的教学中，引导学生从实际问题情境中发现和提出问题，分析问题，建立数学模型并求解问题，在认知系统中逐步建立模型思想尤为重要。

2.对模型思想渗透的再思考

（1）为什么要渗透

渗透模型思想是义务教育阶段的数学教育明确的目标要求［3］，应在发展学生的符号意识、几何直观、运算能力、推理能力、模型思想和应用意识等方面有所作为。因此，教师应注重在解决实际问题的过程中渗透模型思想，使学生体会一元二次方程是刻画现实世界的有效模型。

（2）如何渗透

数学模型思想渗透教学一般分为模型回顾、模型建构、模型应用三个环节。模型回顾是指新模型学习前的认知基础，通过问题唤醒学生的数学模型认知经验，为建立新模型奠定基础。模型建构是指在原有认知基础上的同化或顺应，建立新的数学模型。模型应用是指运用新的数学模型解决实际问题，使学生在建立数学模型解决实际问题的过程中体会模型思想。

本节课模型思想渗透的三个环节以此为基础，具体为：（1）模型回顾，引导学生回顾曾经研究过的一元一次方程模型，唤醒经验；（2）模型建构，以问题1、问题2为载体，驱动学生自主建构二次函数、一元二次方程、一元一次不等式（组）等数学模型，体会不同数学模型的特征及内在联系；（3）模型应用，呈现四个拓展性的问题情境，促使学生运用习得的数学模型解决新的实际问题。

3.对培养建模能力的再理解

在初中阶段，教师越来越重视在教学中渗透模型思想，但如何渗透模型思想、哪些教学内容适合渗透、渗透到什么程度等问题依然困扰着很多教师。事实上，渗透模型思想的教学价值指向培养学生的数学建模能力。需要说明的是，在初中数学教学中，渗透模型思想、开展综合实践活动是培养初中生数学建模能力的主要路径，其中渗透模型思想是常规的、适切的、有效的培养路径。

【参考文献】

［1］孙凯.在数学建模中建立知识结构——《一元二次方程》单元复习课教学设计与思考［J］.教育研究与评论，2021（2）：45-47.

［2］史宁中.数学思想概论（第一辑）——数量与数量关系的抽象［M］.长春：东北师范大学出版社，2008：1.

［3］周立栋.数学模型思想及其渗透教学［J］.上海教育科研，2015（10）：64-66.

*本文系江苏省教育科学“十三五”规划2020年度课题“初中生数学建模能力培养与评价的实践研究”（B-b/2020/02/104）的研究成果。