面向对象的多尺度加权联合稀疏表示的高空间分辨率遥感影像分类
洪 亮,冯亚飞,彭双云,楚森森
1. 云南师范大学地理学部,云南 昆明 650500; 2. 西部资源环境地理信息技术教育部工程研究中心,云南 昆明 650500; 3. 云南省地理空间信息技术工程技术研究中心,云南 昆明 650500; 4. 昆明市信息中心, 云南 昆明 650506; 5. 南京大学地理信息科学系, 江苏 南京 210023
高空间分辨率遥感影像具有较高的空间分辨率和较少的光谱波段数,使得地物的类内光谱方差增大,类间方差减少,不同地物的光谱统计分布更加复杂[1]。遥感影像空间分辨率的显著提高,使地物具有丰富的几何细节、形状和纹理等特征,提高了地物在这些特征空间中的可分性,国内外学者将Gabor[2]、MPs(morphological profiles)[3-4]、DMPs(differential morphological profiles)[5]、MRF(Markov random field)[6]、LBP(local binary pattern)[7]、像素形状指数(pixel shape index,PSI)[8]、对象相关指数(object correlative index,OCI)[9]和形状大小指数(shape size index,SSI)[10]等特征用于高空间分辨率遥感影像分类,提高了地物的分类精度。然而,相关研究表明特征空间维数增加有时并不会增加地物的可分性,反而会引起特征空间的数据冗余,导致地物的分类精度提高不显著,甚至会降低分类精度[11-12]。针对上述问题,支持向量机(support vector machine,SVM)[13],随机森林(random forest,RF)[14-15],条件随机场(conditional random field,CRF)[16],稀疏表示(sparse representation classification,SRC)[17-18]等机器学习方法被应用于高空间分辨率遥感影像分类,上述分类方法的分类精度显著优于传统基于像素级光谱特征的统计方法,但是无法解决分类结果中存在的胡椒盐噪声现象。针对基于像素方法的胡椒盐噪声现象,研究人员提出一种以对象作为基本处理单元的影像分析方法—面向对象的影像分析方法(object-based image analysis,OBIA),并应用于高空间分辨率遥感影像分类[19-20]。文献[21]利用OBIA方法和高分辨率航空影像进行县级尺度的土地覆盖制图,与基于像素方法的结果相比,OBIA获得最高的制图精度。文献[22]提出一种结合面向对象和随机森林的森林资源分类方法,试验结果表明面向对象的方法高于传统基于像素的SVM方法,并且有效抑制椒盐效应。文献[23]分析了样本集大小、分割尺度和特征选择对OBIA分类精度的影响,认为影像分割尺度直接影响OBIA方法的分类精度。文献[24—26]从上述3个方面改进OBIA方法,提高了地物的分类精度,取得较好的结果。但是,由于地表复杂性,OBIA方法中影像分割的最优尺度选择仍然是OBIA方法面临的关键问题。近年来,深度学习(deep learning,DL)成为高分辨率遥感影像信息提取领域的研究热点[27-28]。文献[29]将训练好的深度神经网络(deep convolutional neural networks,DCNNs)模型应用于高分辨率遥感影像的土地利用分类,得到较高的分类精度。文献[30]针对像素级DCNNs模型很难获得精确地物边界的问题,提出一种面向对象的CNN算法,应用于3个典型高分辨率遥感数据集,试验结果表明该方法适合于复杂城市背景的遥感制图。但是目前遥感领域还缺少大规模地物训练数据集(如计算机领域的ImageNet),这也是制约深度学习方法广泛应用于遥感影像信息提取的瓶颈问题。同时,稀疏表示理论也引起了国内外研究者的广泛关注,已经在计算机领域的人脸识别、目标检测、图像检索和恢复等方面取得巨大成功[31]。由于稀疏表示方法能有效解决高维特征空间的维数灾难和小样本问题,遥感领域的研究人员也将稀疏表示理论应用于遥感影像的恢复和重建、分类和目标识别等方面,并取得较好的效果。文献[32]最先将SRC方法应用于高光谱遥感影像(hyperspectral image,HSI)分类,提出一种联合稀疏表示分类算法(joint sparse representation classification,JSRC),该算法考虑中心像素的邻域像素空间信息,获得较好的分类结果。文献[33]提出一种非局部加权联合稀疏表示分类算法(weighted joint sparse representation classification,WJSRC),采用非局部空间优先权重扩展文献[32]的JSRC算法,该算法在地物边界区域获得较好的分类精度。文献[34]针对文献[32—33]中的JSRC算法采用固定窗口确定中心像素的邻域空间信息的不足,提出了一种形状自适应的联合稀疏表示分类算法(shape-adaptive joint spares representation classification,SAJSRC),该算法根据局部方差自适应确定中心像素的邻域大小,试验证明该算法的结果优于文献[32—33]。文献[35]提出一种差异性加权SRC算法,该算法计算像素与各字典的差异距离作为权重,在高光谱遥感影像分类中取得较高的分类精度。文献[36]考虑了邻域像素对中心像素的影响具有差异性,提出了一种加权联合最邻近SRC算法,采用两个标准的高光谱遥感影像进行试验,取得比传统SRC算法更高的分类精度。文献[37]根据多类型特征(光谱、形状和纹理等)有利于提高分类精度的原理,提出一种多特征核稀疏表示算法,采用了空间、Gabor、LBP和DMPs 4类特征,试验取得较高的分类精度。随着新型高光谱-高空间分辨率航空遥感影像的出现,国内外学者将面向对象方法与SRC结合,提出了以超像素(影像对象)作为基本处理基元的SRC算法,获得比像素级SRC算法更好的地物分类结果[38-39]。在文献[38—39]的基础上,研究者针对面向对象分析方法中的多尺度特性,提出了多尺度区域级的SRC算法[40-41],该算法通过考虑多尺度区域特征,每个尺度分别采用JSRC算法,最终融合多尺度分类结果来提高地物分类精度。综上所述,稀疏表示能有效处理高维光谱和空间特征,并且从像素级SRC算法向对象级SRC方向发展,成功应用于高光谱遥感影像的地物分类,但是稀疏表示应用于高空间分辨率遥感影像的地物分类还鲜有报道。
1 理论与算法
文献[38,42—43]研究已经表明基于超像素(影像对象)的JSRC比基于像素的JSRC算法具有更高的分类精度,但是以影像对象作为处理基元的JSRC算法面临关键问题之一就是如何获得影像对象的最优分割尺度。遥感影像中真实土地覆盖地物十分复杂,包括多尺度的地物对象,单一尺度很难表达复杂地物。文献[40—41]提出了一种多尺度对象级JSRC算法,并应用于遥感影像分类,取得较高的地物分类精度。上述多尺度对象级JSRC算法只是对不同尺度的对象特征进行简单的堆叠处理,并没有考虑不同尺度的对象特征对分类结果影响的差异性。综上所述,稀疏表示方法能有效处理高光谱遥感影像中的高维光谱和空间特征,然后高空间分辨率遥感影像除了少数的光谱特征,还具有高维的空间结构、纹理、和形状特征。基于此,本文基于面向对象影像分析方法的框架,利用高空间分辨率遥感影像的地物多尺度特性和SRC算法优点,提出一种面向对象的多尺度加权稀疏表示的高空间分辨率遥感影像分类算法(object-oriented multi-scale weighted sparse representation classification,OMWSRC)。该算法充分利用高空间分辨率遥感影像的多尺度多类型的高维特征(光谱、空间结构、形状、纹理和对象特征等),并考虑多尺度对象中的尺度内对象和尺度间对象的特征对地物分类的影响,根据对象空间异质确定多尺度权重。OMWSRC算法主要包括:①影像对象的多尺度分割和特征提取;②多尺度权重计算;③构建面向对象的多尺度加权联合稀疏表示模型,具体技术流程如图1所示。
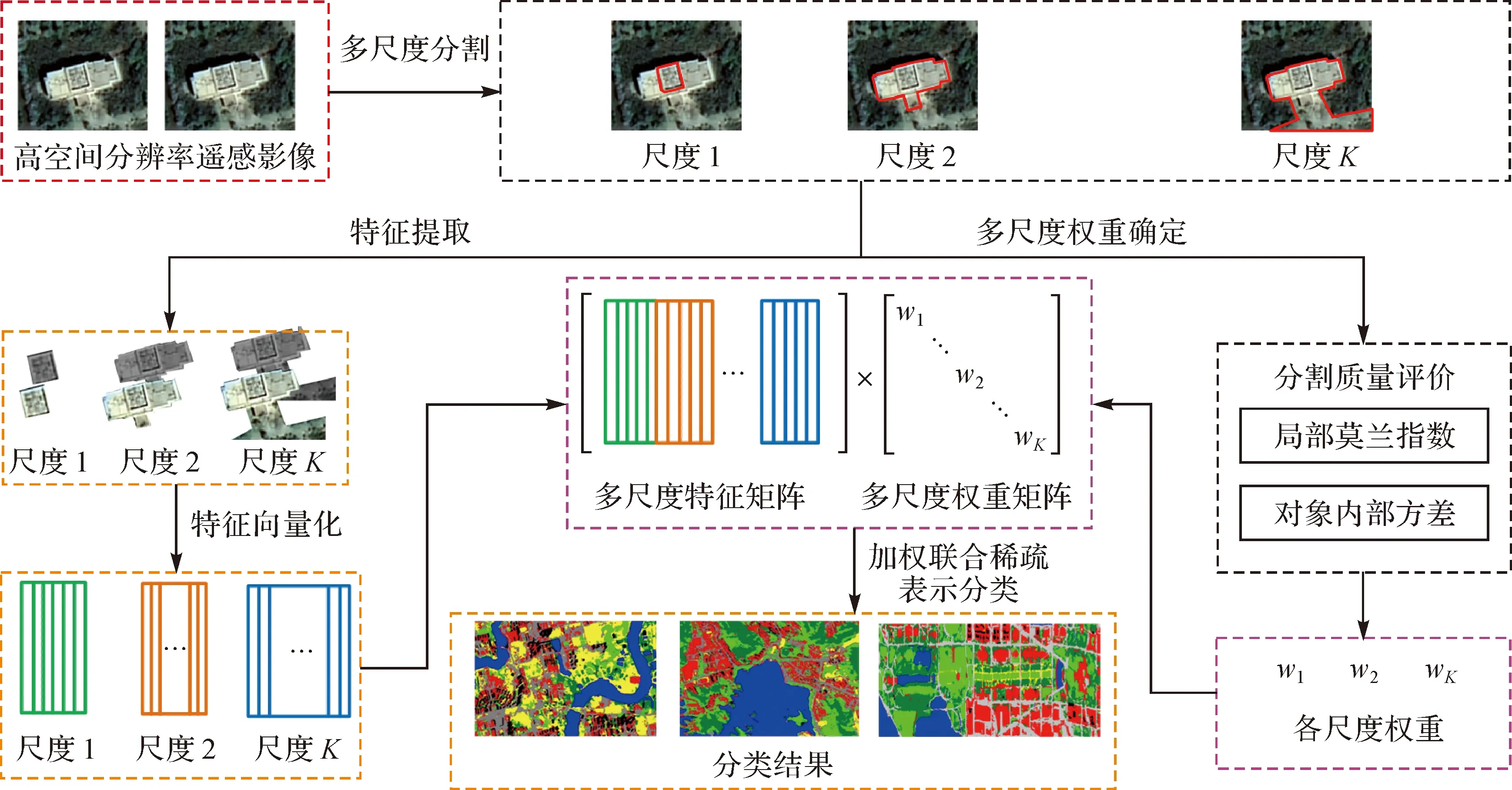
图1 OMWSRC算法流程Fig.1 The flowchart of OMWSRC algorithm
1.1 影像对象的多尺度分割和特征提取
影像分割就是基于同质性或异质性准则将一幅影像划分成若干有意义互不重叠的同质区域(影像对象)。由于地物具有多尺度特性,影像多尺度分割已经成为面向对象影像分析方法的关键步骤,目前常用多尺度分割算法包括商业软件eCongition中的分形网络演化(fractal net evolution approach,FNEA)[43]和均值漂移(MeanShift)算法,本文采用FNEA算法获得影像对象的多尺度分割结果。
相关研究已经表明,通过增加空间结构、形状、纹理和对象等多类型特征有利于提高高空间分辨率遥感影像的地物分类精度[8-9]。本文采用了光谱、空间结构、形状、纹理和对象等5种类型特征,其中,光谱特征包括影像4个光谱波段;纹理特征采用灰度共生矩阵(gray level co-occurrence matrix,GLCM)[44]和小波纹理(wavelets texture)[45];空间结构特征采用LBP[46],结构特征集(structural feature set,SFS)[47]和EMPs(extended morphological attribute filters)[48];对象特征包括面积、周长、边界指数和形状指数。
1.2 多尺度权重计算
OBIA的核心思想就是通过增加影像对象的空间特征、纹理特征、形状特征和尺度间空间关系推理提高分类精度,因此,影像分割的质量直接影响OBIA的分类精度,并且两者具有明显的正相关性。鉴于上述想法,在OMWSRC算法中,根据多尺度分割结果的分割质量测度计算不同尺度对象特征的各自权重,通过权重控制各尺度分割在分类中的重要性,从而提高地物分类精度。影像对象分割质量的测度主要包括影像对象与邻域对象的异质性和影像对象本身的空间异质性。
影像对象间的异质性采用文献[49]提出的局部对象莫兰指数(local Moran 's I,LMI),具体计算如式(1)所示
(1)
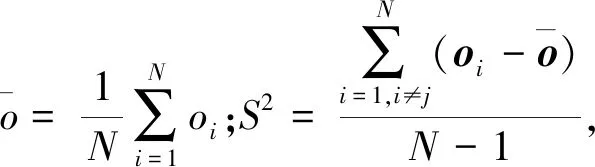
对象内部方差V可以表示对象内部同质性程度,具体计算如式(2)所示
(2)
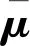
FNEA算法根据异质性准则和尺度阈值参数合并形成多尺度分割结果,并且多尺度分割结果具有层次关系,本文以最小尺度的影像对象作为最小处理基元,最小尺度的对象i根据层次关系确定其他大尺度的对象j,其中i∈j,假设分割K个尺度,对象i的多尺度集为{i1,i2,…,ik}。根据式(1)和式(2),计算对象i在尺度k的局部对象莫兰指数LMIik和对象内部方差Vik,其中k=1,2,…,10。由于局部对象莫兰指数LMIik和对象内部方差Vik的取值范围不一致,对这两个对象异质性指标进行归一化处理后为NLMIik和NVik,具体计算公式为
(3)
(4)
式中,(LMIik)max和(LMIik)min分别表示局部对象莫兰指数LMIik的最大值和最小值;(Vik)max和(Vik)min分别表示对象内部像素方差的最小值和最大值。
根据对象间和对象内的异质性构建影像分割质量指数H,具体计算如式(5)所示
Hik=2-(NLMIik+NVik)
(5)
NLMIik和NVik分别表示对象间和对象内的空间异质性,上述两个指标与分割质量成反比,根据式(5)把影像分割的质量指数Hik与分割质量转化为正相关关系,Hik的取值范围为[0,2]。Hik表示对象i在尺度k的分割质量,值越大表示分割的质量越好。综上所述,本文采用分割质量指数作为OMWSRC算法的权重wik=NHik,方便统一量纲,对权重进行归一化处理,具体如计算式(6)所示
(6)
式中,wik表示对象i在尺度k中的权重,影像对象的分割质量越好,在分类中相应对象特征赋予更大权重。所以,在分类中根据不同尺度的影像对象分割的质量差异,不同尺度的对象特征赋予不同权重。
1.3 面向对象的多尺度加权联合稀疏表示分类
在OMWSRC建模中,选择最小尺度(k=1)的分割对象作为分类基元,k=1尺度的对象i1内的像素一定在k≥1尺度的对象ik中,再将最小尺度的对象i1内像素和该对象对应的其他分割尺度结果中对象内像素共同构成一个多尺度像素特征矩阵YMS=[Y1,Y2,…,Yk],其中Yk表示k尺度中的i对象内所有像素的特征。根据式(2)—式(6)可以计算得到对象各个尺度的权重wik,为了给对象内像素集Yk赋予权重,需要把wik扩展为一个对角矩阵Wk=dig[replicate(wik,n)],其中replicate(wik,n)表示wik复制n,n为尺度k中的i对象内像素个数,多尺度重权矩阵表示为WMS=dig[W1,W2,…,WK]。根据像素级WJSRC算法和多尺度权重计算,OMWSRC算法具体计算如式(7)所示
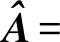
(7)
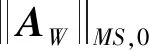
(8)

2 试验结果与讨论
2.1 试验数据
本文采用2个国产GF-2高空间分辨率遥感影像数据集和1个高光谱-高空间分辨率航空遥感数据集(Washington D.C.数据)作为试验数据,试验1和试验3为国内外典型城市复杂场景,试验2为国内县城简单场景。试验1采用2015年2月12日获取的武汉市东西湖区GF-2影像,选取10 000×20 000像元窗口作为研究区,4 m分辨率的假彩色和参考样本如图2(a)所示。试验2采用2015年4月16日获取的杭州市淳安县GF-2影像,选取10 000×20 000像元窗口作为研究区,4 m分辨率的假彩色和参考样本如图2(b)所示;试验3采用1995年8月23日HYDICE传感器获取的华盛顿哥伦比亚区(Washington D.C.)高光谱-高分辨航空影像,选择307×1280像元窗口作为研究区,该数据包含191个波段,波段范围为0.4~2.4 μm,选取波段60、波段27和波段17合成2 m分辨率的假彩色影像,假彩色影像和参考样本如图2(c)所示。试验1和试验2的地物类型包括:裸地、道路、房屋、水体、树木、草地和阴影等7种,每种地物随机选择200个像元作为训练样本,其余像元作为验证样本,详见表1。试验3的地物类型包括:水体、草地、屋顶、砾石路、道路、阴影和树木等7种,每种地物随机选择200个像元作为训练样本,其余像元作为验证样本,详见表2。
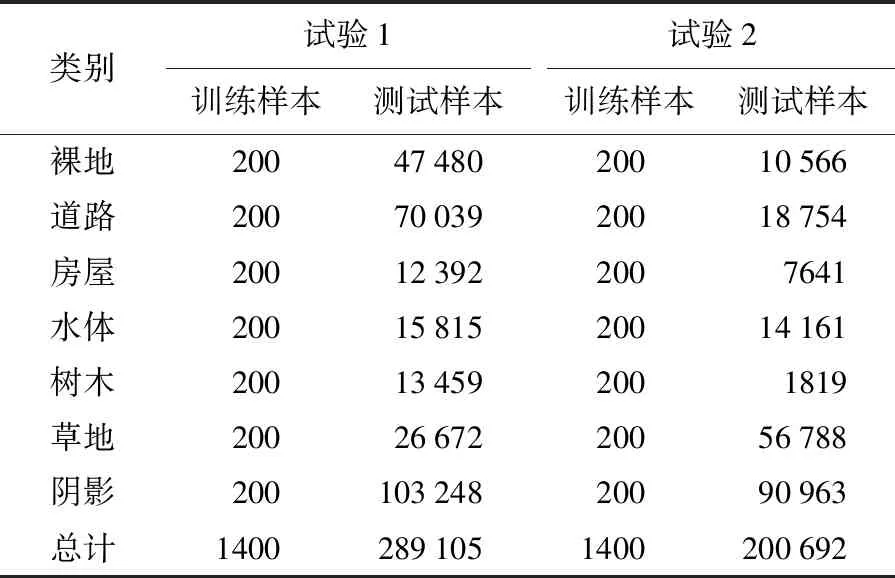
表1 试验1(武汉市影像)和试验2(杭州市淳安县)的训练和测试样本数目Tab.1 Training and testing data sets for experiment 1 and 2 (Wuhan and Hangzhou)

图2 试验数据Fig.2 Experimental data

表2 试验3(Washington D.C.)的训练和测试样本数目Tab.2 Training and testing data sets for experiment 3 (Washington D.C.)
2.2 试验结果分析
2.2.1 试验参数设置
将本文提出的OMWSRC算法与SVM[51]、Multi-SVM[52]、SRC[32]、JSRC[32]、MSSR(multiscale superpixel-based sparse representation)[40]、OMSRC(object-oriented multi-scale sparse representation classification)[41]和DL(deep learning)[53]等分类算法进行对比试验。其中,OMSRC是本文提出的OMWSRC算法没有考虑多尺度权重因子特殊情况下面向对象SRC分类算法,即式(8)中权重WMS设置为单位矩阵后的算法,通过两者的对比试验验证多尺度权重在分类中的效果。
(1) 各种分类算法的最优参数设置如下:基于交叉验证的网络搜寻方法确定SVM和Multi-SVM算法中的惩罚系数C和间隔参数[31,54],核函数采用高斯核函数,相关试验采用LIBSVM开源软件包来实现[54];试验1的SRC、JSRC、MSSR、OMSRC和OMWSRC算法的稀疏系数K0分别设置为1、10、10、3和1,试验2的K0分别设置为1、10、8、1和1,试验3的K0分别设置为1、9、8、1和1,试验1、2和3中的JSRC算法邻域窗口大小分别设置为3×3、7×7和3×3;本文采用的DL算法是一种基于对象的DL算法,利用ROC-LV算法[55]计算试验1、2和3的最优分割尺度分别为31、33、29,采用2层网络结构,输入层大小为100,卷积核大小为20,池化层的大小为3×1,全连接层大小为100。
(2) 影像分割和特征提取参数设置:FNEA分割算法的Shape参数为0.5,Compactness参数为0.5,Scale参数从1至50,步长为2,采用文献[56]提出ROC-LV算法计算最优的3个尺度作为多尺度分割结果,试验1的分割尺度大小为19、31和41,试验2的分割尺度为21、33和47,试验3的分割尺度为17、29和43;GLCM特征提取算法的窗口大小为5×5,方向为0,距离为1,灰度级为8;SFS特征提取算法的光谱约束参数为50,空间约束参数为20;EAP特征提取算法的面积分别设置为100、500、1000、5000,对角线长度设置为10、25、50、100,惯性矩设置为0.2、0.3、0.4、0.5,标准差设置为5、10、15、20,最终获得46维特征,试验1和试验2的试验数据仅有Red、Green、Blue和NIR4个波段,而试验3的试验数据为高光谱-高空间分辨率航空影像,采用主成分分析方法获得4个光谱特征,在本文中3个试验的特征维数都为50。
2.2.2 不同分类算法试验结果对比分析
3个试验的地物分类结果如图3、图4和图5所示,从定量评价指标(总体分类精度(overall accuracy,OA)和Kappa系数)(见表3、表4和表5)分析如下。
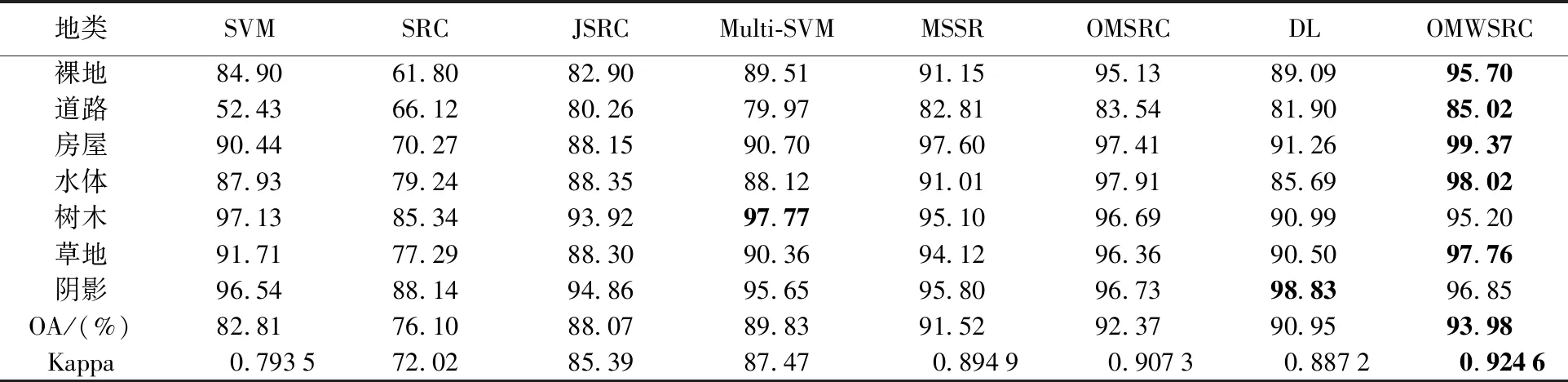
表3 试验1(武汉市)地物分类精度Tab.3 Classification accuracy of experiment 1 (Wuhan) (%)

表4 试验2(杭州)地物分类精度Tab.4 Classification accuracies of experiment 2 (Hangzhou) (%)
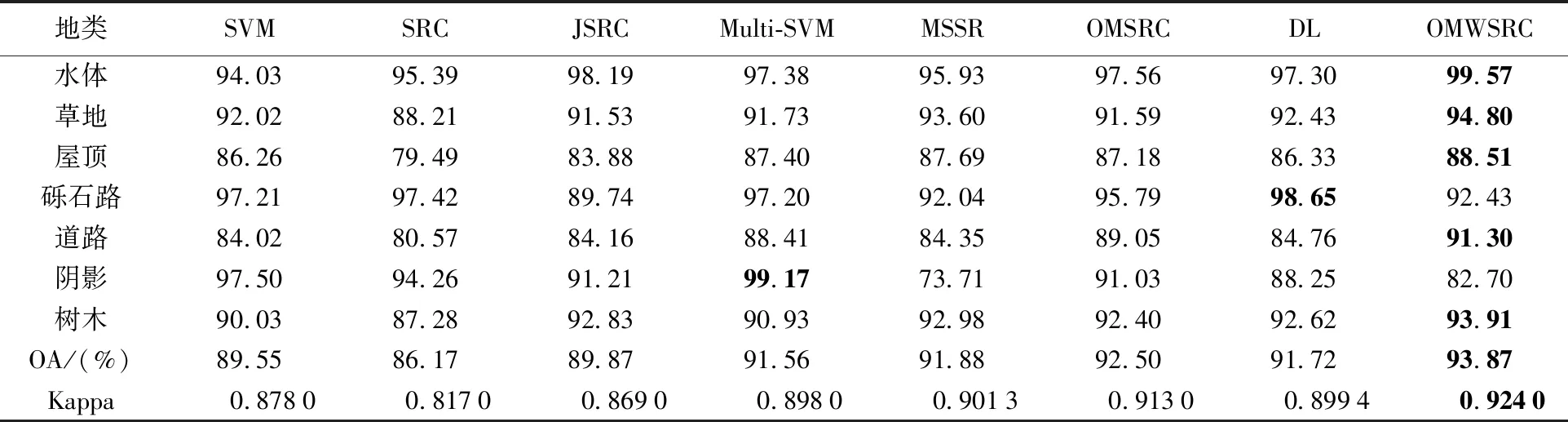
表5 试验3(华盛顿)地物分类精度Tab.5 Classification accuracies of experiment 3 (Washington D.C.) (%)
(1) 在试验1、2和3中,总体上基于对象的方法(MSSR、OMSRC、DL和OMWSRC)的分类精度高于基于像素的方法(SVM、SRC、JSRC和Multi-SVM)。
(2) 直接把稀疏表示(SRC)方法用于高空间分辨率遥感影像分类相对于传统的SVM算法并没有明显的优势,在城市复杂场景(如试验1和试验3)中,SRC算法比SVM算法的总体分类精度分别降低了6.71%和3.38%,在县城简单场景(如试验2)中,SRC比SVM方法的总体分类精度提高了1.35%;但是,在稀疏表方法中加入邻域空间信息显著提高了分类精度,在试验1、试验2和试验3中,JSRC算法的总体分类精度比SRC分别提高了11.97%、5.07%和3.7%。
(3) DL的分类精度总体要优于传统的分类方法(SVM、SRC、JSRC、Multi-SVM),在复杂城市场景(试验1和试验3)中的效果更加明显,但是DL方法的分类精度要低于基于对象级多尺度稀疏表示方法(MSSR、OMSRC和OMWSRC)。
(4) 在高分辨率遥感影像分类中,由于地物具有多尺度特性,基于对象多尺度的稀疏表示算法(MSSR、OMSRC和OMWSRC)的分类精度要高于基于像素的稀疏表示算法(SRC和JSRC),基于多尺度算法(Multi-SVM、MSSR和OMSRC)的地物分类精度高于基于单尺度算法(SVM、SRC和JSRC)。
(5) 考虑不同尺度地物对分类的影响,OMWSRC的分类精度高于不考虑尺度权重的稀疏表示分类算法(MSSR和OMSRC)。在试验1中,OMWSRC的OA精度比MSSR和OMSRC分别提高了2.46%和1.61%;在试验2中,OMWSRC的OA比MSSR和OMSRC分别提高了2.16%和1.04%;在试验3中,OMWSRC的OA精度比MSSR和OMSRC分别提高了1.99%和1.37%。特别在试验1、试验2中的复杂地物(道路、房屋和屋顶)分类中,该算法的分类精度相对于MSSR和OMSRC算法具有明显提高。在试验1中,OMWSRC算法的道路分类精度比OMSRC和MSSR算法分别提高了2.21%和1.48%,房屋的分类精度分别提高了1.77%和1.96%;在试验2中,OMWSRC算法的道路分类精度比OMSRC和MSSR算法分别提高了9.77%和1.20%,房屋的分类精度分别提高了3.01%和1.39%;在试验3中,OMWSRC算法的道路分类精度比OMSRC和OMSRC算法分别提高了6.95%和2.25%,屋顶的分类精度分别提高了0.65%和1.33%。
(6) 在3个试验中,本文提出的算法获得最高的分类精度,OA精度分别为93.98%、97.10%和93.87%,Kappa系数分别为0.924 6、0.959 1和0.924 0。在试验1中,本文提出的分类算法在大部分地物(祼地、道路、房屋、水体和草地)中获得了最高的分类精度,仅Multi-SVM和DL方法在树木、阴影和砾石路中分别获得最高的分类精度;在试验2中,除了阴影外,本文提出的算法在地物分类中都获得最高的分类精度。
从定性目视判别结果可知:①基于像素的算法(SVM、SRC和JSRC)都存在严重的椒盐噪声(图3(a)—(d)、图4(a)—(d)和图5(a)—(d),但多尺度特征融合的算法(Multi-SVM)(图3(d)、图4(d)和图5(d))在一定程度上降低了地物分类的椒盐现象,基于对象的算法(MSSR、OMSRC、DL和OMWSRC)都较好地保持了大尺度地物的区域性(如图3(e)—(h)、图4(e)—(h)和图5(e)—(h))。②本文提出的OWMSRC算法(图3(h)、图4(h)和图5(h))与MSSR和OMSRC算法(图3(e)和(f)、图4(e)和(f)和图5(e)和(f))的分类结果相比,本文提出的算法在大尺度地物(水体、祼地、草地等)和小尺度地物(道路和房屋等)的分类效果都得到了明显改善,但是,本文提出的算法并没有很好解决建筑物阴影的错分现象。

图3 试验1(武汉市影像)分类结果Fig.3 Classification results of experiment 1 (Wuhan)

图4 试验2(杭州)分类结果Fig.4 Classification results of experiment 2 (Hangzhou)
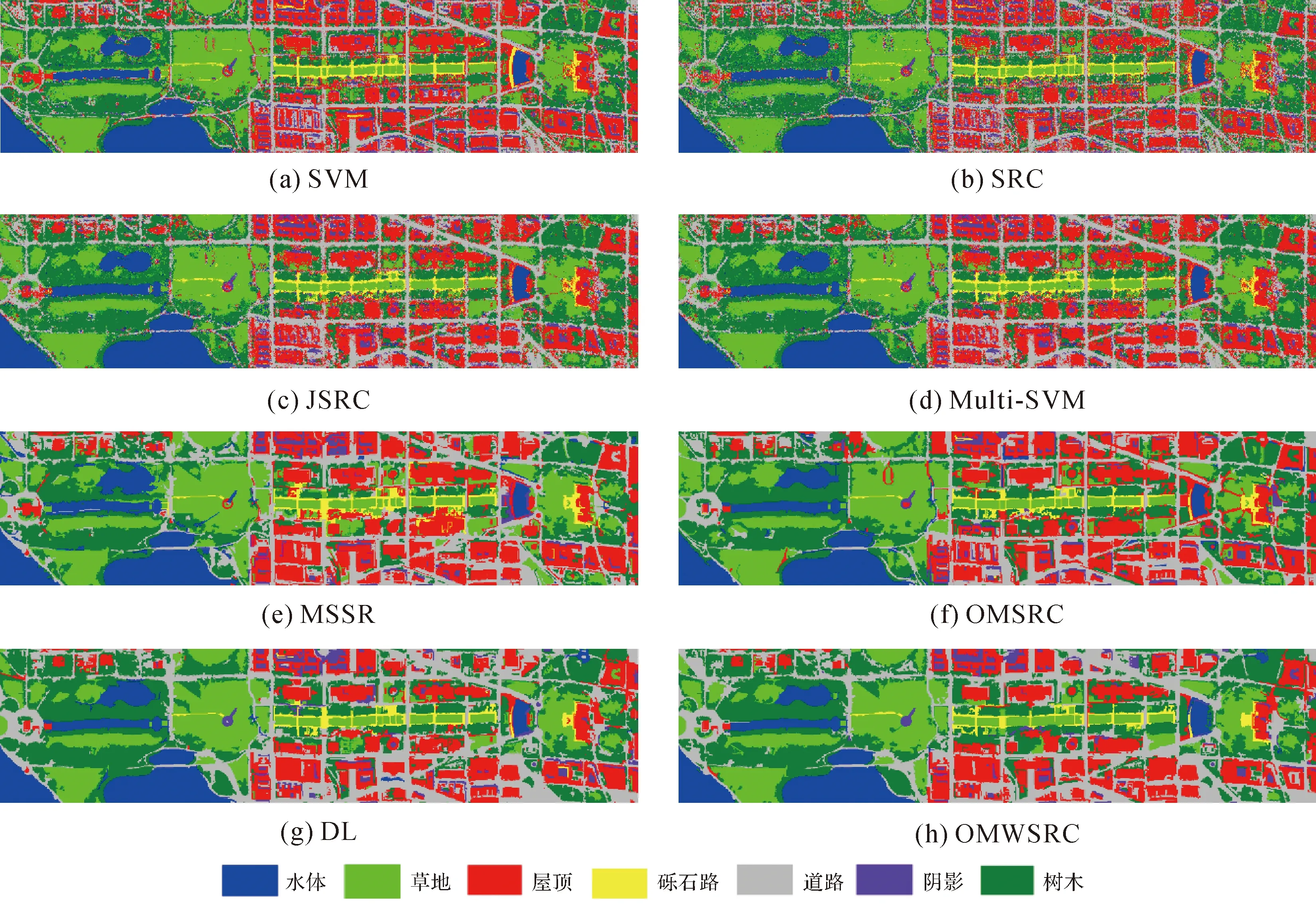
图5 试验3(华盛顿)分类结果Fig.5 Classification results of experiment 2 (Washington D.C.)
2.2.3 稀疏表示分类算法的参数讨论
从文献[32]可知,影响稀疏表示算法的参数主要包括特征维数(feature dimensions,FD)和稀疏系数(sparse level,SL)两个参数,本节将详细分析两个参数对各种稀疏表示算法分类精度的影响。
(1) 特征维数对分类结果的影响分析。3个试验中的光谱、纹理和形状特征维数共计50,利用文献[56]的ReliefF算法根据特征的重要性进行特征选择,分为3、10、20、30、40、50这6个特征组。采用传统的SVM和稀疏表示算法(SRC、JSRC、MSSR、OMSRC和OMWSRC)进行对比试验,试验结果如图6所示。从3个试验的结果可知:①当特征维数从3维增加到10维时,SVM和各种稀疏表示算法的地物分类精度都有较大幅度的提高。②当特征维数从10维增加到20、30或40维时,各种分类器的地物分类精度表现小幅度的提高,并出现一定的波动。③当特征维从40维增加到50维时,SVM、SRC、JSRC和MSSR算法的地物分类精度表现相对比较平稳,但是OMSRC和OMWSRC两种算法的地物分类精度得到较大提升,证明了基于对象的多尺度稀疏表示算法对特征维数增加具有较好的稳健性。

图6 特征维数对稀疏表示算法的影响Fig.6 Effects of feature dimensions on sparse representation algorithms
(2) 稀疏系数对分类结果的影响分析。稀疏系数作为影响稀疏表示算法的另一个主要参数,设置初始稀疏系数为1,并以1作为步长进行增加,稀疏系数范围为1~10,其他的参数相同,共设置10组对比试验,试验结果如图7所示。从3个试验的结果可知:①在SRC中当稀疏系数为1时,地物分类精度达到最高,分别为76.1%、89.22%和86.22%。②在OMWSRC中当稀疏系数为1时,地物分类精度达到最高,分别为93.98%、97.10%和92.44%。③MSSR和JSRC两种算法随着稀疏系数增加,地物分类精度呈现上升的趋势,然而稀疏系数对OMSRC算法的分类精度影响不大。在稀疏表示算法中,稀疏系数对算法分类精度的影响并没有表现一定的规律性,需要根据具体场景和算法来确定最佳的稀疏系数。
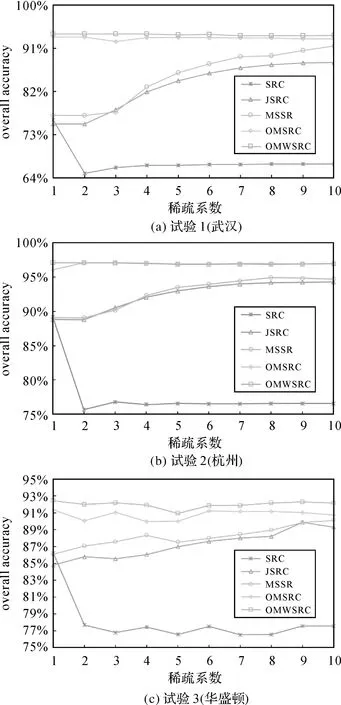
图7 稀疏系数对稀疏表示算法的影响Fig.7 Effects of sparse level on sparse representation algorithms
3 结 论
本文针对高空间分辨遥感影像中地物具有多尺度特性,传统的稀疏表示算法没有考虑不同尺度的对象特征对地物分类精度影响的差异性,提出一种面向对象的多尺度加权的稀疏表示分类算法。通过试验分析,可以得出以下结论:①高空间分辨率遥感影像具有丰富的纹理和形状特征,稀疏表示算法能处理高维的多类型特征,相对其他经典和深度学习分类算法,取得较好的地物分类精度。②本文提出的多尺度加权策略能有效降低错误分割的对象特征在分类中的比重,进而提升了地物分类精度。③本文提出的算法能同时顾及不同尺度的地物特征,发挥多尺度分割优势,在城市复杂和县城简单场景都表现出了优异的性能。
本文研究还存在如下一些问题:①如何根据不同场景,选择最优的纹理和形状特征。②如何选择最优分割尺度作为确定多尺度权重的尺度。③如何自动确定最优的稀疏表示算法中的稀疏系数。④还需要验证本文提出的算法在其他高分辨率遥感影像和大尺度复杂场景的泛化能力。

