基于超像素和低秩的协同稀疏高光谱解混
张帅洋,华文深,刘 杰,李 刚,王强辉
(中国人民解放军陆军工程大学 石家庄校区 电子与光学工程系,石家庄 050003)
引 言
高光谱图像(hyperspectral image,HSI)包含丰富的光谱和空间信息,在农业、工业、军事等方面都有广泛的应用[1-5]。但受遥感仪器空间分辨率的限制以及地物复杂分布的影响,高光谱图像中常常包含大量混合像元,即一个像元往往同时包含几种地物,这严重限制了高光谱数据的处理和应用。若只包含一种地物,则该像元称之为端元(endmember,EM)。为此光谱解混技术得到了广泛的发展,即求解各个像元所包含的地物种类以及它们所占的比例。
光谱解混模型主要有线性和非线性两种。其中线性解混模型简单易解灵活性高,因此得到广泛的应用[6]。基于线性解混模型的算法主要分为几何学、统计学、稀疏回归三大类。稀疏解混认为混合像元是光谱库中端元的线性组合,不需要估计端元数目和提取端元[7]。近年来,稀疏解混技术引起了研究者们的广泛关注,涌现出了大量有效的稀疏解混算法。变量分裂增广拉格朗日算法[7](sparse unmixing algorithm via variable splitting and augmented Lagrangian,SUnSAL)是较为经典的稀疏解混算法,但其稀疏性不足且受光谱库互相关性影响较大。另外,SUnSAL未利用丰富的空间信息。为了提高解混精度,研究者们主要从如何加强稀疏性约束以及如何充分利用空间信息这两个方面着手。协同稀疏解混算法[8](collaborative SUnSAL,CLSUnSAL)施加全局联合稀疏性约束,提高了解混精度。ZHENG等人[9]采用重权重策略,WANG等人[10]引入双权重策略,以及参考文献[11]中直接解决l0范数等,这些算法都增强了稀疏性约束,并取得了较好的解混结果。IORDACHE等人[12]提出变量分裂增广拉格朗日全变差算法(sparse unmixing via variable splitting augmented Lagrangian and total variation,SUnSAL-TV),第1次将空间信息引入稀疏解混,但其易导致边缘模糊和过平滑现象。LI等人[13]引入双边滤波,ZHANG等人[14]提出空间不连续权重稀疏解混算法这些都有效缓解了全变差正则项的不足。此外,HUANG 等人[15]提出联合稀疏块回归和全变差正则化的解混算法,ZHANG等人[16]提出光谱空间权重稀疏解混算法(spectral-spatial weighted sparse unmixing,S2WSU)等等。这些算法都说明了稀疏性和空间信息对提高解混精度至关重要。
经典的协同稀疏解混算法认为所有的像元享有同样活跃的端元集,但实际端元往往存在于空间匀质区域。而基于全变差正则项的利用空间信息的方法容易导致过平滑的现象。为了增强稀疏性约束以及利用空间信息,并且克服上述问题,本文中提出基于超像素和低秩的协同稀疏解混算法(superpixel and low rank for collaborative sparse unmixing,SLRCSU)。对高光谱图像进行超像素分割,并在每个超像素内执行协同稀疏解混,既增强了稀疏性约束,又克服了传统稀疏解混的不足。使用低秩约束代替全变差约束来利用空间信息从而克服了过平滑问题。
1 基于超像素和低秩的协同稀疏高光谱解混算法
1.1 超像素分割
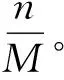
s1=‖yi-yj‖2
(1)
式中,yi和yj代表像元i和j的光谱向量,s1表示光谱距离;(ai,bi)和(aj,bj)分别代表像元i和j的空间位置,s2表示空间距离;α为空间距离与光谱距离之间的权重,s表示像元i和j的综合距离。一般而言,α的值为常数,这里设定为0.5。首先选定M个初始聚类中心,在每个聚类中心的搜索区域内计算各个像元到聚类中心的距离。把像元归为距离聚类中心最近的那一类,每一轮类别划分结束之后计算各个类别的均值作为新的聚类中心,若新聚类中心与原来的相同则聚类结束,否则重新聚类。关于SLIC算法更详细的介绍可以参见参考文献[17]。
1.2 SLRCSU算法
对高光谱图像进行超像素分割之后,对每个超像素施加协同约束,并添加低秩性约束来利用空间信息,其解混模型如下:
(X≥0)
(4)
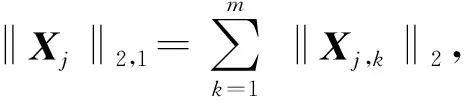
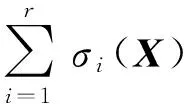
式中,lR+(X)为正向量空间R+的指示函数,当X∈R+时,lR+(X)=0,否则lR+(X)=+∞。直接求解(5)式是非常困难的,为此采用分离变量增广拉格朗日算法进行求解。令V1=AX,V2=X,V3=X,V4=X,则(5)式可等效为:
(V1=AX,V2=X,V3=X,V4=X)
(6)
令V≡(V1,V2,V3,V4),B=diag(-I),G=[A,I,I,I]T,其中I为n×n的单位矩阵,则可构建如下拉格朗日函数:

(7)
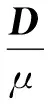
S(Q,ε)=φsoft(diag(σ1,…,σr),ε)ψ
(8)
式中,soft表示软阈值函数soft(y,τ)=sign(y)·max{|y|-τ,0}。则求解(7)式的算法流程及各个变量的迭代更新公式见表1。

Table 1 Algorithm flow of alternating direction multiplier method to solve equation (7)

2 结果与分析

RSRE的值越大解混精度越高。所有算法均在配备有Intel core 5处理器、2.3GHz主频率、12GB内存的笔记本电脑上通过MATLAB R2018a运行。
2.1 模拟数据实验
所构建的模拟数据为包含75×75个像元的数据立方体。为了简化计算对光谱库进行裁剪,使光谱库中任意两物质的夹角不小于4.44°。最终得到包含240个原子的光谱库。从光谱库中随机选取5个原子作为本次实验的端元。丰度满足非负性约束以及和为1约束,图1为各个端元的真实丰度图。图中方块区域可能是纯净的或者是由几个端元混合而成。背景区域由5个端元混合而成,所占的比例分别为0.1149,0.0741,0.2003,0.2055和0.4051。为了更加符合真实地物的分布情况以及检测各个算法的抗噪声能力,在模拟数据中分别添加信噪比(signal-to-noise ratio, SNR)为20dB,30dB和40dB的高斯白噪声。各个算法的参量均调整到合适大小以得到每个算法的最佳性能。表2为各个算法所得到的RSRE值、所需要的时间以及对应的参量值。其中λTV为SUnSAL-TV算法对应的全变差正则项参量。图2中为信噪比30dB时各算法的解混丰度图的对比。
从表2中能够看出,在所有信噪比下SLRCSU都能够获得最好的解混性能。相比经典的SUnSAL-TV算法,其解混精度提高了40%左右,并且SLRCSU所用的时间仅为SUnSAL-TV的一半。从图2中能够看出,SUnSAL-TV和SLRCSU都能够获得清晰纯净的背景,但在端元2的解混丰度图中SLRCSU所得方块数量明显多于SUnSAL-TV。因此,模拟数据实验能够证明所提算法的有效性。

Fig.1 Fractional abundances of the endmembers for simulated data

Table 2 RSRE, time and parameter values of each algorithm for simulated data
2.2 真实数据实验
真实数据使用机载可见/红外成像光谱仪于1997年收集的Cuprite数据集。它被广泛应用于解混算法对比。为了简化计算,使用大小为250×191的数据子集。该子集共包含224个波段,去除低信噪比以及水吸收较高的波段(1~2,105~115,150~170,223~224)后仅保留188个波段。图3为Cuprite数据集各物质的分布图。它被制作于1995年,因此只能用来定性评价解混性能。各个算法的参量均调整到合适大小。表3为各个算法的参量值及所用时间。图4为从数据集中选取的2种典型代表物质(buddingtonite,chalcedony)的解混丰度图。

Table 3 Parameters and times corresponding to each algorithm for real data
从图4中能够看出,SUnSAL-TV算法所得到的解混丰度图存在明显的边缘模糊现象,并且其背景存在较多杂质。其它算法的背景均较为清晰纯净。从矿物Chalcedony的解混丰度图中能够看出,SLRCSU算法的解混结果在相对应的区域丰度更高,更符合真实地物的分布情况。因此,真实数据实验同样能证明所提算法的有效性。

Fig.2 Abundance maps obtained by each algorithm with SNR 30dB

Fig.3 Distribution map of different substances in the Cuprite dataset

Fig.4 Abundance maps obtained by each algorithm for Cuprite
3 结 论
针对传统协同稀疏解混算法的不足以及全变差正则项易引起边缘模糊和过平滑的问题,提出了一种基于超像素和低秩的协同稀疏解混算法。对高光谱图像进行超像素分割,把分割后的超像素作为协同单元,同时通过低秩约束来挖掘高光谱图像中的空间信息。所提出的算法不仅克服了以上不足,同时增强了稀疏性约束以及对空间信息的利用。实验结果表明,与其它算法相比,该算法获得了更好的解混结果。

