基于改进麻雀算法的最大2维熵分割方法

柳长安，冯雪菱，孙长浩，赵丽娟

(华北电力大学 控制与计算机工程学院，北京 102206)

引 言

图像分割是图像处理的关键步骤[1]，分割依据主要包括阈值[2-3]、区域[4-5]、边缘[6-7]。阈值分割原理是根据某种规则求出最优阈值，根据最优阈值进行分割，因其性能相对稳定且实现简单而得到广泛使用。1979年提出的Otsu法只考虑了灰度信息。后来提出的最大Kapur熵分割法优于Ostu算法，但抗噪性较差[8]。除了Kapur熵，一些学者引入交叉熵[9]、Renyi熵[10]等进行图像分割,虽然提升了图像分割质量，但是1维分割方法性能提升有限。LIU等人[11]针对1维分割精度较低的情况提出2维Otsu算法，考虑像素邻域信息，改善了1维Otsu算法性能。ABUTALEB[12]提出2维最大熵方法，在分割性能上优于1维最大熵分割方法，但是大大增加运算时间。

群体智能优化算法以其独特的生物群体行为生存方式，提供了更多优化问题的新思路。自“群体智能”概念被首次提出，众多学者提取生物种群特征，凝练出新的群智能优化算法。随着近些年群体智能优化算法的蓬勃发展，群体智能算法广泛应用于解决参量最优化问题上，其中包括蚁群算法(ant colony optimization,ACO)[13]与粒子群算法(particle swarm algorithm,PSO)[14]两大经典优化算法，以及萤火虫算法(firefly algorithm，FA)[15]、灰狼算法(grey wolf optimization，GWO)[16]、蚁狮算法(ant lion optimizer,ALO)[17]、鲸鱼算法(whale optimization algorithm，WOA)[18]、正弦余弦算法(sine cosine algorithm,SCA)[19]等新型优化算法。

受麻雀在自然中觅食策略的启发，2020年,XUE等人提出麻雀搜索算法(sparrow search algorithm，SSA)[20]。SSA算法相比其它算法具有稳定性较高、收敛精度较好和一定程度上避免陷入局部最优等优点，但是SSA算法收敛速度较快容易导致陷入局部最优解的情况，依然有概率得到不可行解。因此,本文中提出了基于精英反向的改进型t分布麻雀算法(improvedt-distribution SSA,ITSSA)，加强麻雀粒子之间的交流，加快算法收敛速度，同时使用精英反向学习策略保证麻雀种群均匀性并且增强全局搜索的能力，引入t分布算法前期增加全局搜索能力，后期增加局部寻优能力，采用萤火虫算法，进一步增加种群多样性。将ITSSA算法应用于最大2维熵分割中，实验表明，此方法可提高图像分割实时性，在峰值信噪比和特征相似度上得到极大提升。

1 麻雀搜索算法

SSA是一种新型的群体智能优化算法，每只麻雀位置对应一个解，更新方式可分为向当前最优位置靠近和向原点靠近。作为群居鸟类的麻雀，与其它鸟类相比，具有聪明且记忆力强的特点。麻雀搜索算法通过麻雀搜索食物和反捕食操作进行参量优化，初始位置用以下矩阵表示：

式中，n是麻雀的个数，d是待优化变量的维度。第i只麻雀位置为Xi=[xi,1,…,xi,j…,xi,d]。麻雀的适应度表示如下：

式中，f(Xi)表示麻雀个体的适应度。

麻雀群体分为3种角色：发现者、追随者、警戒者。发现者通常负责整个麻雀群体食物来源的寻找并且为加入的追随者提供觅食方向。当报警值大于安全值，发现者将追随者带到安全区域。在每次迭代中，发现者的位置更新如下：

式中，R是当前迭代次数，Rmax是最大迭代次数，α1是(0,1]范围的随机数，Q是服从正态分布的随机数，L是各元素都为1的1行多维矩阵。Ra∈[0,1]和Rs∈[0.5,1.0]分别代表预警值和安全阈值。

在每次迭代中，追随者位置更新如下：

式中，Xb和Xw分别表示最优位置和最劣位置，A是元素为1或-1的1行多维矩阵。

随机产生麻雀群体的警戒者，占整个麻雀群体的10%～20%，其位置更新如下：

Xi(R+1)=

式中，β1是步长控制参量，服从(0,1)的正态分布；α2是[-1,1]范围的随机数；β2是最小常数，避免当fn=fb时，分母为0的情况发生。fn,fb和fw分别代表当前适应度、最佳适应值和最劣适应度。

2 融合自适应t分布的多策略麻雀搜索算法

2.1 自适应t分布

t分布[21]又称为学生分布，其曲线形态和自由度参量k有关，概率密度函数如下：

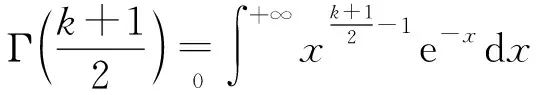
当k=1时，t分布为柯西分布；当k→∞时，t分布为高斯分布。t分布融合柯西分布和高斯分布的特点，在算法运行过程中通过改变k的值可以获得不同的变异幅度。在算法运行的初始阶段，t分布因为k值较小近似于柯西分布变异，t分布具有较强的全局探索能力；在算法运行的中间阶段，t分布从柯西分布变异向高斯分布变异逐渐过渡，结合两者优势；在算法运行后期，t分布因为k值较大近似于高斯分布，t分布具有较强的局部搜索能力，有利于算法高效找到全局极值点。

本文中采用自适应t分布变异，第i个体原位置Xi变异公式如下：

XiT=Xi+ζ·t(R)

(7)

式中，XiT代表t变异后个体位置，ζ代表自适应因子，t(R)为以当前迭代次数R为参量的t分布。

2.2 精英反向学习策略

反向学习策略(opposition-based learning,OBL)[22]已被证实可以有效提高智能优化算法搜索能力，提高近50%找到全局最优解的概率，其主要思想是求问题可行解的反向解，对原可行解和反向解进行评估，选出更优解作为下一代个体。精英反向学习(elite opposition-based learning,EOBL)利用精英个体包含更多信息的特点，构造当前种群的反向种群，选取当前种群和反向种群中更优质的个体作为初始解。设当前群体的精英个体位置为:

Xi′=[xi,1′,…,xi,j′,…,xi,d′]

(8)

则精英个体的反向解为:

Xi′*=α3[min(xi,j′)+max(xi,j′)]-Xi′

(9)

式中，α3是(0,1)范围的随机数。利用随机生成的α3值可以生成多个精英反向解，如果生成的反向解超出上下边界值，则重置反向解。

2.3 萤火虫算法

萤火虫算法[15]模拟萤火虫发光行为，亮度弱的萤火虫受亮度强的萤火虫吸引，进行移动从而更新位置得到新的位置，亮度强的萤火虫进行扰动操作。萤火虫亮度L和吸引力r如下式所示：

式中，f(Xi)代表第i只萤火虫适应度值,也是其亮度，γmax代表萤火虫间的最大吸引度,μ是光强系数，lA,B表示两个萤火虫之间的距离。

当萤火虫A被萤火虫B吸引时，萤火虫A的位置如下式：

XA=XA+γ×(XA-XB)+λ(α4-0.5)

(11)

式中，XA和XB分别表示萤火虫A和萤火虫B的位置。λ∈[0,1]为步长因子，α4为(0,1)服从均匀分布的随机数。

最亮萤火虫S的位置更新公式如下：

XS=XS+λ(α4-0.5)

(12)

式中，XS表示最亮萤火虫的位置，(12)式让萤火虫一定程度上避免过早陷入局部最优。

2.4 融合自适应t分布的多策略麻雀搜索算法

针对麻雀算法的不足，首先利用反向学习策略生成反向解加入种群，扩大算法搜索范围。将迭代次数作为t分布的自由度参量，增加种群多样性，提高算法的全局探索能力和局部开发能力。与此同时，选择多个最优个体，利用精英反向学习策略选择发现者，提高种群质量，提高算法收敛速度。追随者位置更新易受发现者位置更新情况影响，为进一步提高收敛精度和寻优效果，利用萤火虫机制扰动追随者，改善争夺觅食过程中易陷入全局优化能力。在保留麻雀算法3种角色和竞争机制的前提下，采取动态策略，设置转换概率p，将精英反向策略与萤火虫算法和自适应t分布变异在一定概率下交替执行，动态更新位置，改善基础麻雀算法容易陷入局部最优的缺陷，达到增强全局寻优能力的目的，得到更优质的解。具体实现步骤如下。

(1)初始化参量：种群数量、最大迭代次数Rmax、转换概率p、发现者比例Dp、警戒者比例Ds、警戒者预警值Rs等;(2)应用第2.2节中的反向学习策略生成反向解加入麻雀初始种群，选取最优个体作为最终的初始种群;(3)计算每只麻雀适应度并排序;(4)应用第2.2节中的反向学习选择策略选择发现者，其余作为追随者，获取精英麻雀动态边界，更新发现者和追随者的位置,随机选择侦察警戒者，更新其位置;(5)计算并更新每只麻雀适应度值;(6)判断变异条件:若随机数r∈[0,1]小于转换概率p，则利用第2.1节中的自适应t变异公式更新每只麻雀适应度值；若r≥p,则应用第2.2节中的精英反向策略更新发现者，应用第2.3节中的萤火虫算法扰动追随者，应用原式更新警戒者的适应度值;(7)对步骤(6)的越界个体做越界处理,比较新适应度值和原值，若新适应度值优于原值，则更新位置和适应度值，反之，则保留;(8)判断当前迭代次数R是否达到最大迭代次数，若是，则循环结束，输出结果，反之，返回步骤(6)。

3 基于ITSSA的2维最大熵图像分割

图像分割的最佳阈值即为彻底分离目标和背景的像素边界。基于最大熵的阈值分割方法就是将熵值作为目标函数，让图像分割后的目标区域和背景区域熵的和达到最大值。1维最大熵虽然处理速度较快，但是仅考虑自身像素的灰度信息，而忽略区域相关性，当噪声严重时，因此表现出较差的分割效果以及抗噪性能。2维最大熵应运而生，结合像素点和区域灰度特征，提取图像有用信息。

2维最大熵[23-24]原理如下：假设输入图像大小为M×N，待分割图像为I(x,y)，像素点8×8邻域灰度均值为g(x,y),且1≤x≤M，1≤y≤N。设I(x,y)=u，g(x,y)=v，且1≤u,v≤L-1(灰度范围L=256)。

式中，quv表示图像值为u且区域灰度均值为v的像素点数频率,puv是其对应的概率[20]。

输入图像2维直方图如图1所示。

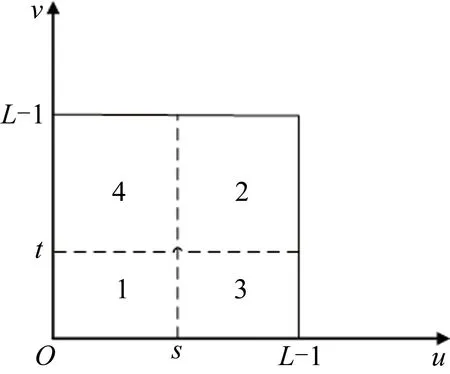
Fig.1 2-D histogram

区域1和区域2代表目标和背景，区域3和区域4代表噪声和边界。假设分割的阈值为(s,t)，则区域1目标区域和区域2背景区域概率分别为：

区域1和区域2的2维熵分别为：

定义分割图像的2维熵函数为：

H=H1+H2

(16)

当2维熵函数取最大值时，对应的最优分割阈值(s*,t*)应满足:

H(s*,t*)=max{H}

(17)

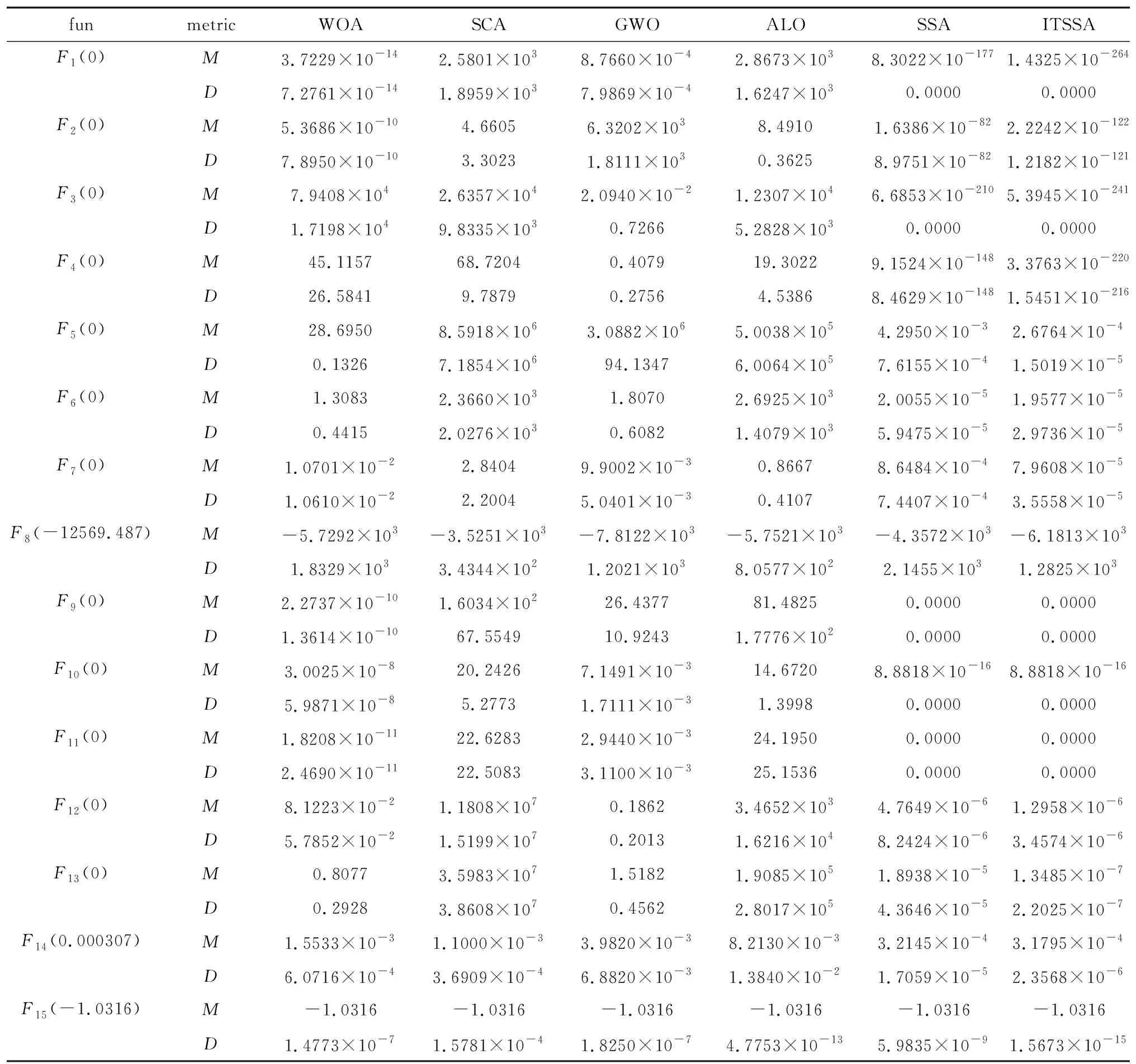
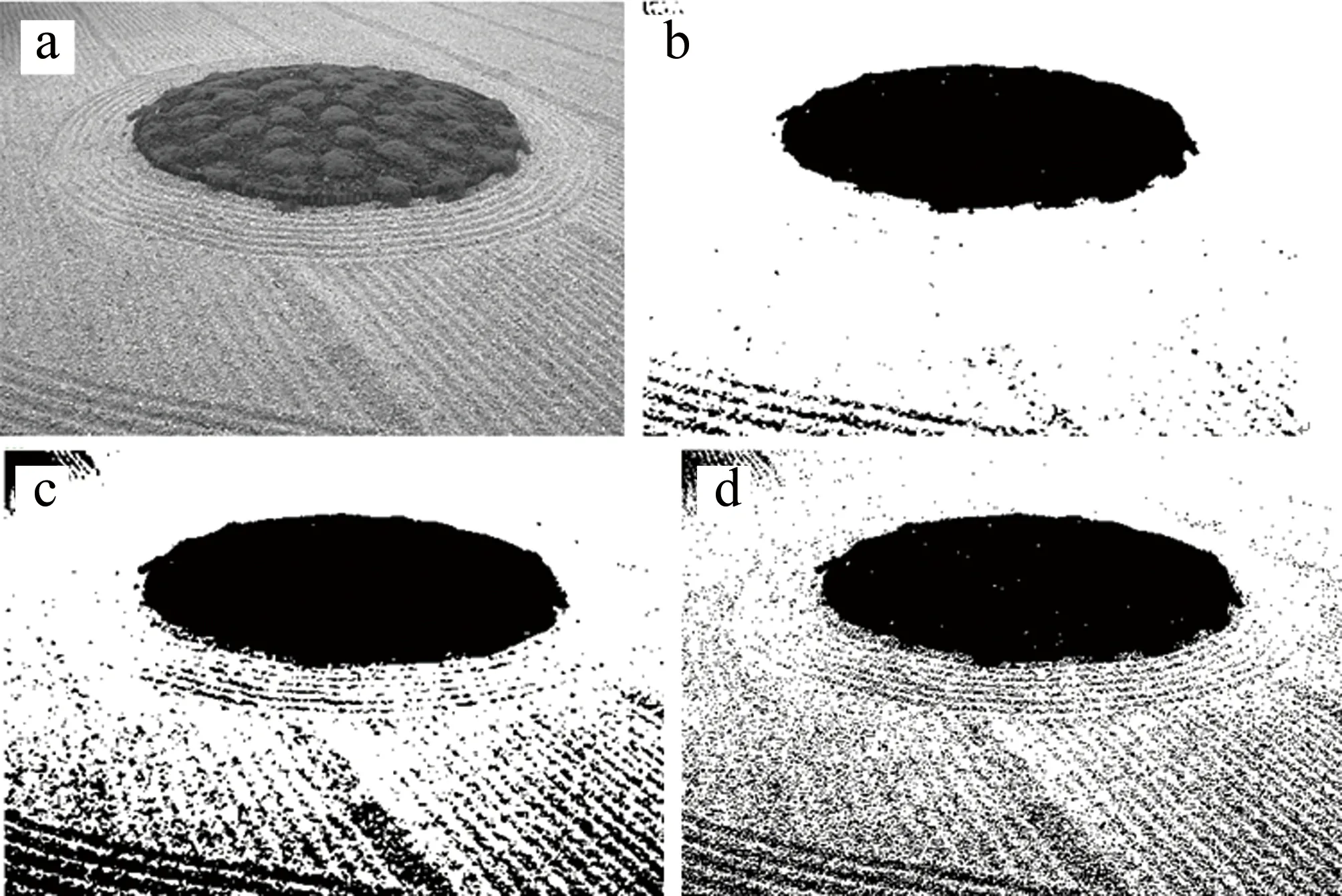
式中，0

为了解决2维阈值分割计算时间长及传统智能优化算法常陷入局部最优、收敛速度慢的问题，提出一种基于精英反向的自适应t分布麻雀算法的2维最大熵图像分割方法。

令ITSSA的适应度函数为:

fITSSA=H

(18)

通过融合自适应t分布的多策略麻雀搜索算法让适应度函数取最大值，此时的s值和t值为最优解，即为图像最优分割阈值(s*,t*)。具体步骤如图2所示。

Fig.2 Flow chart of maximum 2-D entropy based on ITSSA

4 实验仿真和结果分析

4.1 基准函数测试

为了验证本文中算法的正确性和有效性，使用SCA,ALO,WOA,GWO,SSA和ITSSA分别测试15个基准函数进行比较，充分考察ITSSA算法的寻优能力。各算法参量取值见表1，测试函数名称及参量设置见表2。表1中，b是对数螺旋形状常数，as是自适应调整常数，ag是收敛因子。表2中，F1～F7为单峰函数；F8～F12为不定维多峰函数；F13～F15为固定维度多峰函数。其中，α5和α6为u函数的参量;φi和φi为φ数组和φ数组中i位置的数值;e为常数。单峰函数仅有一个极大值或极小值，用于检验算法的收敛速度和精度，多峰函数具有多个局部或全局最优解，用于检验算法全局探索能力和开发能力。本文中仿真实验的运行环境为Core i7 CPU、Windows 10操作系统，内存为8GB，处理器速度为3.2GHz。算法在MATLAB R2020a软件上运行。在对比测试实验中，为保证实验结果的客观，设置各算法种群数量均为50，最大迭代次数为100。

Table 1 Algorithm parameter value

Table 2 Benchmark functions

选取各算法在基准函数独立运行20次的均值M和标准差D作为实验结果，其中均值反映算法寻优能力和精度，标准差反映算法的鲁棒性。

本文中的算法ITSSA与其它智能算法实验结果对比见表3，测试函数收敛情况见图3。括号中为函数最优值。对于单峰函数F2,F4,F5和F7，ITSSA寻优均值和标准差比其它算法高出多个数量级，说明ITSSA具有较高的求解精度、求解速度和鲁棒性。对于F1和F3，ITSSA和SSA具有相同的标准差，但是ITSSA比SSA的均值高出多个数量级。求解F6时，SCA和ALO求解能力很差，与理论最优值存在较大误差。而ITSSA在SSA的基础上，相比WOA和GWO求解表现更好，且寻优精度变化不大。

对于不定维多峰函数F8，各算法求解能力均不理想，ITSSA寻优能力仅次于GWO。对于F9～F11，ITSSA在迭代次数20以内可以找到最优解，不易陷入局部最优，优于其它算法。对于F12～F14，ITSSA求解能力最优。对于固定维多峰函数F15，各算法都收敛到-1.3016，ITSSA标准差最小，具有最好的稳定性。

综上所述，ITSSA算法在单峰和多峰函数上的寻优性能均优于SCA,ALO,WOA,GWO和基础的SSA算法。这主要得益于精英反向策略、自适应t分布以及萤火虫机制，通过这些方法让ITSSA算法能有效平衡全局和局部寻优能力，一定程度上避免了算法后期陷入局部最优，让ITSSA算法在求解速度、求解精度和稳定性方面均表现出较好的性能，具有较好的寻优能力。

Table 3 Comparison of test results of six algorithms

4.2 基于ITSSA的2维最大熵分割方法

为验证ITSSA2维最大熵分割的有效性，选取经典的rice图(见图4)、pepper(见图5)、伯克利数据集中图86016(见图6)和113016(见图7)进行对比分析。采用峰值信噪比(peak signal-to-noise ratio，PSNR)、特征相似性(feature similarity index，FSI)[25]、各算法运行时间对图像分割质量和算法性能进行评价。其中，峰值信噪比是基于像素均方差的图像相似性的评价指标，PSNR越大，代表图像失真越少；特征相似性是一种基于图像低级特征理解图像这一事实的相似性评价指标，FSI越接近1，代表图像相似度越强。PSNR和FSI定义如下：

式中，I(x,y)和I*(x,y)分别代表原图像和分割后的图像。

Fig.3 Convergence graph of the benchmark functions

Fig.4 Segmentation results of image rice

Fig.5 Segmentation results of image pepper

Fig.6 Segmentation results of image 86016

Fig.7 Segmentation results of image 113016

式中，Ψ表示整幅图像的空间域，C(x)代表最大相位，S(x)代表原图像和分割后图像的相似性值。

式中，C1(x)和C2(x)代表原图像和分割后图像的相位；F(x)代表图像特征相似性；G(x)代表图像梯度相似性；G1(x)和G2(x)代表原图像和分割后图像的梯度幅值；ε,δ,K1和K2均为常数。

在rice图的分割实验中，ITSSA优化的2维最大熵在2维最大熵基础上提高了峰值信噪比且在结构相似性指标上提升31.2%。由图4可以看出，本文中算法误判的像素比其它算法少且米粒轮廓最清晰。在pepper图的分割实验中，本文中分割出更清晰的辣椒，且3种指标优于其它算法，峰值信噪比增加20%。对于伯克利数据集中的86016和113016，虽然2维Otsu比基础的2维Kapur在峰值信噪比指标和特征相似度表现更好，但是保留的图片细节大大减少，耗时过久。本文中提出的算法不仅在3种评价指标上表现更好，改善了113016图错分马匹的现象，也保留了86016图和113016图更多草地和马匹细节，分割轮廓上有更好的表现。与此同时，大大缩短了2维最大熵分割耗时时间，对于256×256的图像，将分割图像总时间达到耗时最少的效果(见表4)。

Table 4 Comparison of values obtained by different segmentation algorithms

5 结 论

针对麻雀种群角色少、寻优精度不足的现象，提出了一种基于自适应t分布的多策略改进麻雀算法。首先利用反向机制引导算法跳出局部最优，然后将自适应t分布变异引入位置更新，发挥其扰动能力。与此同时，采用精英反向策略提高发现者质量，扩大搜索区域，引入萤火虫机制扰动麻雀位置，提高全局优化能力并且增加种群多样性。融合ITSSA和最大2维熵分割方法，缩短了原最大2维熵分割方法分割时间，并将峰值信噪比、特征相似性作为评估标准，与2维Otsu法、2维Kapur熵相比，分割性能更好，分割出更清晰目标轮廓的同时保留更多细节。实验表明，基于ITSSA的最大2维熵图像分割方法在一定程度上解决了麻雀算法后期易陷入局部最优的情况和最大2维熵耗时长的缺点，具有较好的应用价值，为群体智能优化算法应用图像分割领域提供参考。在未来研究中，将尝试寻找并改进出性能更优的群体智能优化算法，应用图像分割领域提高分割性能效果。