基于神经网络的光纤温度和应变快速解调方法
王成亮,杨庆胜,李 军,钟巍峰,陈志明
(江苏方天电力技术有限公司,南京 211103)
引 言
传感器能感知外界物理量的变化,是实现设备智能化的基础,也是实现设备的监测系统[1-2]和物联网[3]的基础。传感器类型众多,其中光纤传感器[4-5]由于具有抗电磁干扰、耐高压、电绝缘、尺寸小等优势而广泛应用于科学、工程、技术和生产生活中的多个领域。在光纤传感器中分布式光纤传感器[6-8]基于单根光纤一次测量即可获得光纤沿线的物理场信息,可以有效减小对传感器数量的要求,在针对大型设备和结构体监测时具有较大的优势。
本文中以基于布里渊散射的分布式光纤传感[9-11]为研究对象。虽然布里渊频移、线宽和布里渊散射功率均与光纤的温度和应变有关,但线宽和布里渊散射功率受其他因素干扰较大,只有布里渊频移稳定性较高。通常来说基于布里渊散射的分布式光纤传感均基于布里渊频移解调温度和应变[12]。由于当光纤长度较长,测得布里渊谱较多时如何准确、快速估算布里渊频移成为了关键问题。现有的方法多基于一定的谱模型[13]去拟合布里渊谱,然后估算布里渊频移,其优势是准确性较高、抗干扰能力较强,同时也能估算布里渊线宽和增益峰值,但要涉及到大量的迭代过程,计算速度较慢,不利于提高传感系统的实时性。虽然现有文献中也通过优化初值获得方法、最小二乘的优化算法来提高布里渊频移估算的实时性,但仍然不能避免拟合方法需要多次迭代才能得到优化结果的问题,计算实时性仍不能满足某些情况下的要求。随着人工智能技术的发展,人们逐渐将人工神经网络方法应用于解决科学与工程中遇到的模式识别、预测等各种问题。为了解决光纤布喇格光栅应用中温度与应变都影响中心波长导致的交叉敏感问题,参考文献[14]中实测了不同温度和应变下两支光纤布喇格光栅的中心波长,将训练后的3层人工神经网络用于温度和应变的估算,结果表明,该方法能实现温度和应变的同时测量。参考文献[15]和参考文献[16]中将径向基函数神经网络用于基于布里渊散射的分布式光纤传感中温度的估算,不同扫频间隔下布里渊频移的计算结果验证了该方法的有效性。但是,现有文献中并未对神经网络方法提取布里渊频移时的计算耗时进行研究。
为了解决该问题,本文中将多层前馈人工神经网络(artificial neural network,ANN)[17]引入到布里渊频移的估算中来,反复尝试后确定了合理的神经网络结构、输入及输出量、激活函数和优化算法,采用不同信噪比(signal-to-noise ratio,SNR)、布里渊频移的仿真布里渊谱训练该网络,针对温度和应变沿线波动的布里渊谱分别采用训练完成的神经网络、基于洛伦兹模型的谱拟合法和基于伪Voigt模型的谱拟合法解调获得光纤沿线的温度和应变,系统比较了3种方法的准确性和计算耗时,结果验证了所提方法的有效性。
1 基于布里渊散射的分布式光纤传感技术
光在光纤中传播会发生布里渊散射,通过在入射端检测背向散射的布里渊信号,得到频移与散射光功率的关系,即得到了布里渊谱。在基于布里渊散射的分布式光纤传感中常使用脉冲光,得到的布里渊谱近似满足如下的伪Voigt模型[18]:
g2exp[-(4ln2)(ν-νB)2/(ΔνB)2]
(1)
式中,gB为布里渊增益,ν为频率,νB为布里渊频移,ΔνB为线宽g1和g2分别为洛伦兹和高斯模型布里渊增益峰值。如果入射光脉宽明显大于50ns,则布里渊谱近似满足如下的洛伦兹模型[19]:
式中,g0为布里渊增益峰值。
光纤温度及应变与布里渊频移成线性关系,如下式所示:
δνB=Cν,TΔT+Cν,εΔε
(3)
式中,Cν,T和Cν,ε分别为针对布里渊频移的温度和应变敏感系数,T和ε分别表示温度和应变;ΔT和Δε分别为温度和应变的变化量;δνB为布里渊频移的变化量。如果布里渊频移的变化仅由温度或应变导致,则温度和应变计算方法如下式所示:
设光纤入射端x=0,测点处x=l,则光从入射到背向散射光返回入射端的时间差为Δt,则l可由下式算得:
l=Δtc/(2n)
(5)
式中,c为真空中光速;n为光纤的折射率。
基于(4)式、(5)式以及脉冲光入射到光纤至背向散射光到达对应的时间差,就可以实现分布式测量。
2 基于神经网络的温度、应变快速解调方法
2.1 基于拟合的温度、应变解调方法
布里渊频移估算最为常规的算法是拟合法,它通常分为目标函数的建立和优化两个步骤。通常来说,基于最小二乘拟合算法建立的目标函数如下式所示:
式中,E为误差的平方和;νn,gB,n和en分别为第n个频率值及对应的布里渊增益及误差;N为扫频点数。
基于洛伦兹模型、伪Voigt模型的谱拟合法对应的目标函数属于非线性最小二乘拟合,常采用Levenberg-Marquardt算法[20]进行优化。该算法对应可调变量的调整公式在第2.2节中会有介绍。如果(6)式中的gB分别用(2)式和(1)式表示,则对应的算法分别为基于洛伦兹模型的谱拟合法和基于伪Voigt模型的谱拟合法。算得布里渊频移后根据(4)式即可解调出温度或应变。
2.2 神经网络法
根据原理的不同,神经网络有多个类型,其中最为经典的是多层前馈神经网络,单隐层的多层前馈神经网络结构如图1所示。

Fig.1 Structure of a multi-layer feedforward ANN for Brillouin frequency shift estimation
多层前馈神经网络可以认为由复合函数实现的由网络输入到输出的映射,而布里渊谱到布里渊频移就可以认为是一个映射,另外,单隐层的多层前馈神经网络理论上可以实现任意复杂的映射。因此,本文中尝试采用单隐层的多层前馈神经网络根据布里渊谱上所有增益估算布里渊频移。
如图1所示,输出层仅有单一神经元的神经网络对应的映射可表示如下:
式中,o为输出层神经元的输出;xm为神经网络第m个样本的输入,xm=[xm,1,xm,2,…,xm,N],即xm=[gB,1,gB,2,…,gB,N];N和H分别为输入层和隐层神经元数量(由于输出仅为布里渊频移,故输出层只有一个神经元),注意,输入层神经元数量即为扫频点数;ω1,n,h分别为输入层第n个神经元到隐层第h个神经元的权值;ω2,h分别为隐层第h个神经元到输出层神经元的权值;φ1和φ2分别为隐层和输出层神经元的激活函数,注意所有隐层神经元用同一个激活函数,输出层神经元也是如此;Hh为隐层第h个神经元的阈值。
神经网络的训练就是使如下的目标函数趋于最小化。
式中,M为训练样本数量;tm为针对第m个样本时神经网络输出层神经元输出的目标值。针对以上非线性最小二乘问题,Levenberg-Marquardt算法[20]具有优异的性能,采用它训练时网络变量的调整公式为:
W(k+1)=
W(k)-(JTJ+λI)-1JTe(W(k))
(9)
式中,W为变量构成的列向量,包括权值和阈值;k为迭代次数;e为针对所有训练样本神经网络输出误差列向量,其元素数量为M,则e=[e1,e2,…,eM]T;λ为可调系数,它用于防止Hessian矩阵的近似出现较大误差;I为K阶单位矩阵,K为神经网络中所有变量的数量;J为Jacobian矩阵。
具体实现时,如果变量调整导致E增加,则λ=λ×10并舍弃本次可调变量的调整;否则令λ=λ/10并保留本次可调变量的调整。
一旦神经网络训练完成,则布里渊频移估算时无需继续训练神经网络,仅仅需要计算(8)式所示的复合函数即可,这可以大大减小布里渊频移估算的耗时。类似地,计算得到布里渊频移后根据(4)式即可解调出温度或应变。因此,光纤沿线温度和应变的快速、准确解调取决于布里渊频移的快速、准确估算。
3 方法验证
3.1 神经网络的训练
仿真布里渊谱采用(1)式产生,其中参量的设置如下:线宽为50MHz,扫频间隔为1MHz,g1=g2=0.5,信噪比在5dB~40dB范围内变化(每隔5dB产生一个仿真点),扫频范围为10.62GHz~10.82GHz。在10.7GHz~10.74GHz范围内等间隔产生41个布里渊频移点。神经网络的输入为一个谱上的所有布里渊增益,输出为布里渊频移,因此网络的输入层和输出层神经元数量分别为201和1。网络的训练目标为布里渊频移均方差为1MHz2,隐层和输出层神经元的激活函数均为线性函数。经过反复尝试输出层神经元的数量选择为40。不同信噪比下用于训练的布里渊谱样本如图2所示。图中纵坐标无单位。
训练误差和训练时间与迭代次数的关系见图3。采用训练得到的神经网络,针对不同信噪比下训练样

Fig.2 Brillouin spectra used for ANN training

Fig.3 ANN training error and training time as a function of training epochs
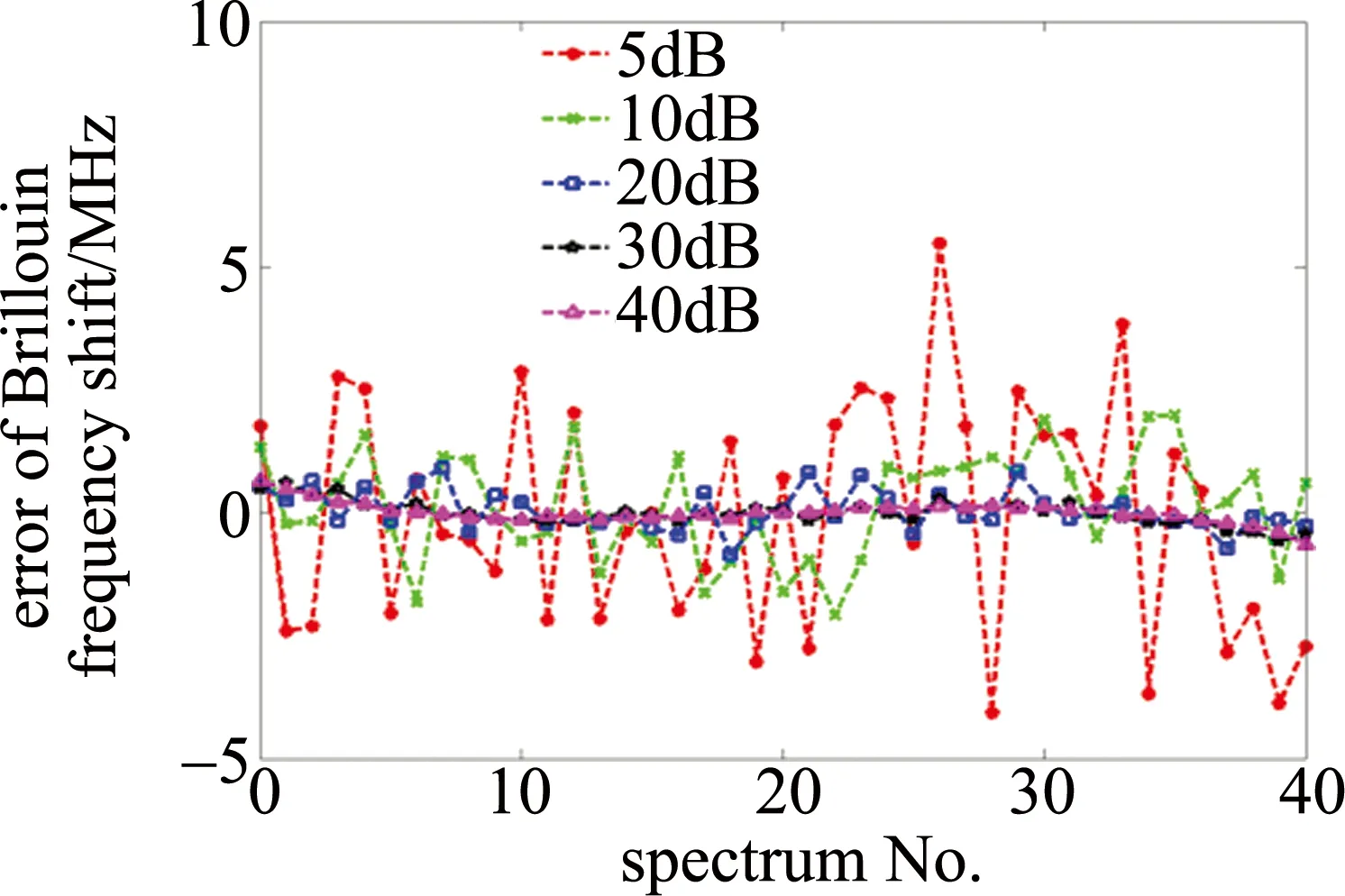
Fig.4 Errors of the trained ANN for Brillouin spectra with different SNRs
本的布里渊频移估算结果如图4所示。
由图2可知,神经网络的训练样本包括了实际中可能遇到的低信噪比到高信噪比的所有情况,这为训练完成后的神经网络能准确估算布里渊频移奠定了基础。由图3可知,随着训练次数的增加网络误差快速下降,最终布里渊频移的均方误差接近于1MHz2。考虑到布里渊频移的温度和应变敏感系数典型值分别为1.12MHz/℃和4.82×10-2MHz/με,对应的温度和应变测量误差分别为略小于1℃和略大于20με,而随着训练次数的增加,训练时间几乎正比增大。由图4可知,随着信噪比的增加神经网络估算得到布里渊频移的误差下降,到信噪比为20dB时布里渊频移的最大误差仅为1MHz左右,已能满足实际要求。以上结果定性上与经典基于谱模型的拟合法相似,从而初步验证了本文中提出的多层前馈神经网络方法用于布里渊频移估算的可行性。
3.2 神经网络的应用
信噪比在7dB~32dB范围内变化(每隔5dB产生一个仿真点),光纤沿线的布里渊频移变化规律如下式所示:
式中,x为光纤位置,单位为m;νB的单位为GHz。其它参量与第3.1节中的一致。
除了采用第3.1节中训练得到的神经网络,也同时采用了基于洛伦兹模型的拟合法和基于伪Voigt模型的拟合法。此外,也实现了径向基函数神经网络方法用于布里渊频移的提取,该网络网络的输入层和输出层神经元数量、训练样本和训练目标与多层前馈神经网络一致,训练后网络成功收敛于训练目标。4种方法算得光纤沿线的布里渊频移如图5所示,布里渊频移误差的统计值如表1所示,不同方法计算时间的统计结果如表2所示。注意,MLF表示多层前馈(multilayer feedforward)神经网络,RBF表示径向基函数(radial basis function)神经网络。如果认为光纤沿线的布里渊频移变化仅由温度或应变导致,则基于估算得到的布里渊频移可以获得不同方法对应光纤沿线温度和应变如图6所示。
由图5结合表1可知,本文中提出的基于多层前馈神经网络的布里渊频移估算方法的准确性与经典的基于洛伦兹和伪Voigt模型的拟合法非常接近,而略高于径向基函数神经网络方法。由表2可知,本文中提出的基于多层前馈神经网络方法的布里渊频移估算耗时远小于经典的基于洛伦兹和伪Voigt模型的拟合法,前者的平均耗时仅分别为后两者的1/689.84和1/757.91;同时也明显小于径向基函数神经网络方法。大量谱的计算结果表明,布里渊频移提取速度受信噪比和扫频点数的影响,故将扫频间隔分别设置为1MHz、2MHz、5MHz和10 MHz,其它参量与本节中的一致,产生不同信噪比(7dB~32dB)和扫频点数(21~201)下的布里渊谱并采用以上4种方法提取布里渊频移。根据计算结果发现,基于多层前馈神经网络方法的布里渊频移估算耗时分别为基于洛伦兹和伪Voigt模型拟合法的1/947.16~1/470.95和1/784.56~1/532.88。即本文中提出的多层前馈神经网络可以快速实现布里渊频移的准确估算。
本文中的研究结果对实现基于温度和应变的大型设备监测系统,甚至配电物联网都有一定的参考价值。

Fig.5 Calculated Brillouin frequency shift of different methods for test samples with different SNRs

Table 1 Statistics results of the error evaluated by different methods for the test sample/MHz

Table 2 Mean computation time of different methods for the test samples/ms

Fig.6 Temperature and strain along the optical fiber obtained by different methods when the SNR is 12dB
4 结 论
对基于布里渊散射的分布式光纤传感中布里渊频移的估算问题进行了研究,提出一种基于多层前馈神经网络的布里渊频移估算方法,采用不同布里渊频移和信噪比下布里渊谱进行训练和验证。对不同信噪比且光纤沿线布里渊频移波动的布里渊谱采用训练完成的多层前馈神经网络、径向基函数神经网络和经典的谱拟合法估算布里渊频移,发现多层前馈神经网络方法的误差与基于洛伦兹模型的拟合法和基于伪Voigt模型的拟合法相近而略小于径向基函数神经网络方法,但计算时间仅分别为前二者的1/947.16~1/470.95和1/784.56~1/532.88。本文中的研究为基于布里渊散射的光纤沿线温度和应变快速测量提供了支持。

