基于最优尺度Logit模型的交通事故形态致因分析*
李泽文,张萌萌,李虹燕
(山东交通学院 交通与物流工程学院,山东 济南 250357)
0 引言
近年来,我国道路事故多发,据中国统计年鉴[1]显示,2019年全国交通事故发生数量为247 646起,比2018年增长了2 709起,同比增长1.11%,造成 67 759人死亡、275 125受伤,道路交通安全问题迫在眉睫。交通事故形态可清晰地描述交通事故参与者之间是以什么样的状态导致事故的发生,故研究其致因对于预防交通事故从而降低事故率具有重要作用。
近年来,许多学者开展了对交通事故形态及其致因方面的研究。高建刚等[2]通过收集交通事故统计数据对道路交通事故形态归纳分析,总结了道路交通事故形态的特点和规律,为我国的道路交通安全研究奠定了基础,该方法得出了照明是影响事故形态的主要因素,此后也被Raynham等[3]采用确定昼夜分界点的方法验证;因为直接观察法需要大量的时间和精力,所以不适用于大样本研究,会影响到结果的代表性,为了更好描述交通事故形态的影响因素,邓瑶望等[4]、王义婷等[5]、陆欢等[6]通过建立二元Logit模型探究事故形态与各因素之间的相关关系,这种方法可以很好地分析分类变量之间的因果联系,但需逐一对各种交通事故形态致因进行分析,步骤繁琐;在二元Logit模型基础上,陶刚等[7]使用粗糙集理论的简约算法求解各因素相对于事故形态的重要度,对各因素对事故形态的影响程度做出判断,但是只针对了简单的算例进行实验,有待检验;而后,随着数据量日渐充实,统计技术手段日新月异[8],王长君等[9]以泊松模型和负二项模型为工具,王羽尘等[10]采用零膨胀泊松和零膨胀负二项模型,Mohammad[11]应用结构方程模型等,对大量的数据进行拟合,分析不同因素对道路交通事故形态的影响程度,取得了很好的效果,应用广泛。但上述研究方法多为直接建立模型,并未对影响因素之间的共线性进行诊断,容易影响模型的精确度。
本文基于最优尺度分析方法判断各因素之间是否存在共线性的问题以及是否具有统计学意义,将具有统计学意义的影响因素与事故形态纳入无序多分类Logit模型,详细分析各因素指标对事故形态的贡献水平,确定不同事故形态的影响因素,以期为交通安全部门提供建议,实现对交通事故的主动预防和预测。
1 交通事故形态影响因素分析
交通事故涉及到人、车、路、环境4大因素系统,各系统又分为不同的子系统和影响因素。基于前人研究成果,并综合考虑交通安全部门的管理和实施方案,本文从道路交通设施和交通环境2个方面入手,拟选取以下因素作为事故模型自变量,如图1所示。
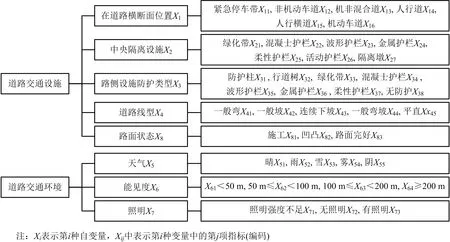
图1 影响因素系统框架Fig.1 System framework of influencing factors
本文抽取某市2017年1月到2019年12月的1 077起交通事故作为基本建模数据,以交通事故形态作为研究对象,选取追尾碰撞、正面碰撞、侧面碰撞以及刮擦碰撞等4类事故形态作为因变量(记为Yr,r=1,2,3,4)进行分析。
针对交通事故形态变量无序、多元的属性,采用无序多分类Logit模型对事故形态影响因素进行分析,且模型在计算过程中会设置虚拟变量,便于检验分类变量(自变量)对因变量的作用,不仅提高模型的精度,也可避免自行设置变量的复杂性。
2 基于最优尺度分析的变量诊断及筛选
2.1 最优尺度分析
最优尺度分析法最早由荷兰Leiden大学DTSS课题组研制[12]。最优尺度分析模型的数学表达如式(1):
(1)
式中:Yr是因变量,表示事故形态种类,r=1,2,3,4,分别代表追尾碰撞、正面碰撞、侧面碰撞以及刮擦碰撞;Xi是自变量,表示交通事故形态的影响因素,i=1,2,…,8,分别代表在道路横断面位置、中央隔离设施、路侧设施防护类型、道路线型、天气、能见度、照明、路面状态;ε为随机误差,在建模的时候引入,用来解释由于数据本身具有测量误差而导致的由模型确定性因素得到的最终结果与实际有所偏差的原因;β0~β8为回归系数,其绝对值越大表明自变量对因变量的影响越大。
最优尺度分析擅长将分类变量不同取值量化处理,从而对变量之间做共线性诊断及显著性分析,简化分类问题。
2.2 自变量共线性诊断以及显著性检验
运用spss软件对数据进行最优尺度分析,结果见表1~2。

表1 模型分析结果Table 1 Analysis results of model
表1中模型的多元相关系数R为0.802,判定系数R2为0.643,表示模型中的自变量可以有效地解释因变量,且在模型的方差分析中P<0.05,说明模型具有统计学意义。
表2给出了各自变量的回归系数、显著性值以及容忍度,其中回归系数表示自变量对因变量影响大小的参数,回归系数越大表明影响越大,不同因素对事故形态的影响程度排序为:
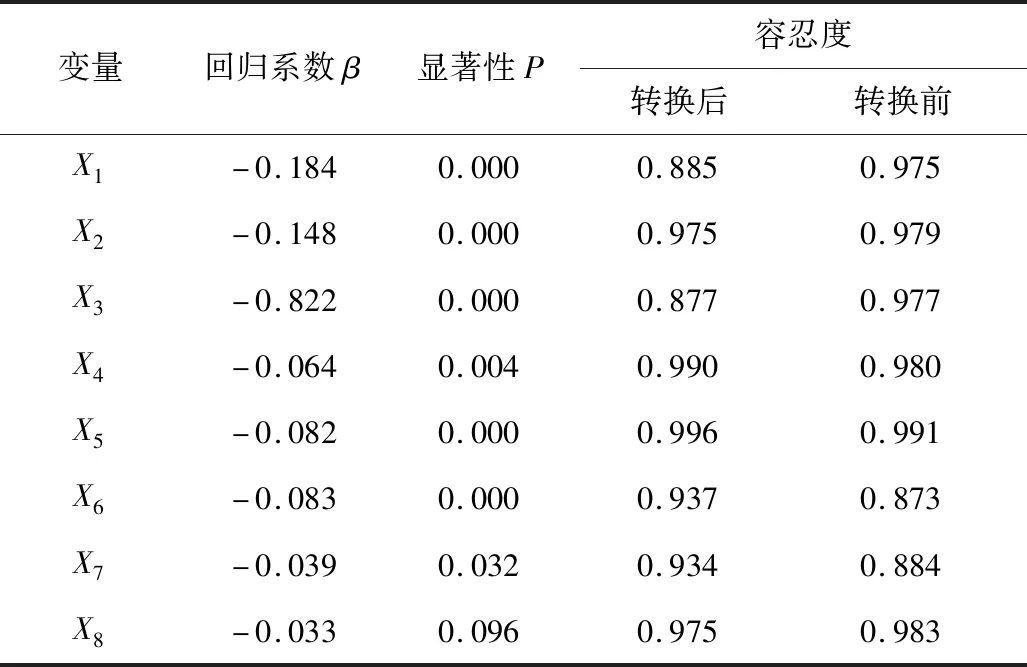
表2 回归分析Table 2 Regression analysis
X3>X1>X2>X6>X5>X4>X7>X8
自变量的显著性可以判断其是否具有统计学意义,当显著性值小于0.05时,则认为在95%的显著性水平下显著,具有统计学意义,反之则没有,路面状态的显著性值为0.096,不具有统计学意义,因此,选择剔除。容忍度反映了自变量的共线性情况,数值越大越好,转换后容忍度均大于0.5,表示各自变量之间不存在多重共线性问题。
上述变量在进入模型之后被量化评分,以此来表示各个类别之间的差距,量化评分近似,则表示影响程度相近,反之影响程度差异大,如能见度量化评分对应如图2所示,可见X61>50 m、50 m≤X62<100 m被给予了相同的量化评分,100 m≤X63<200 m量化评分稍有不同,与X64≥200 m评分差距非常大。
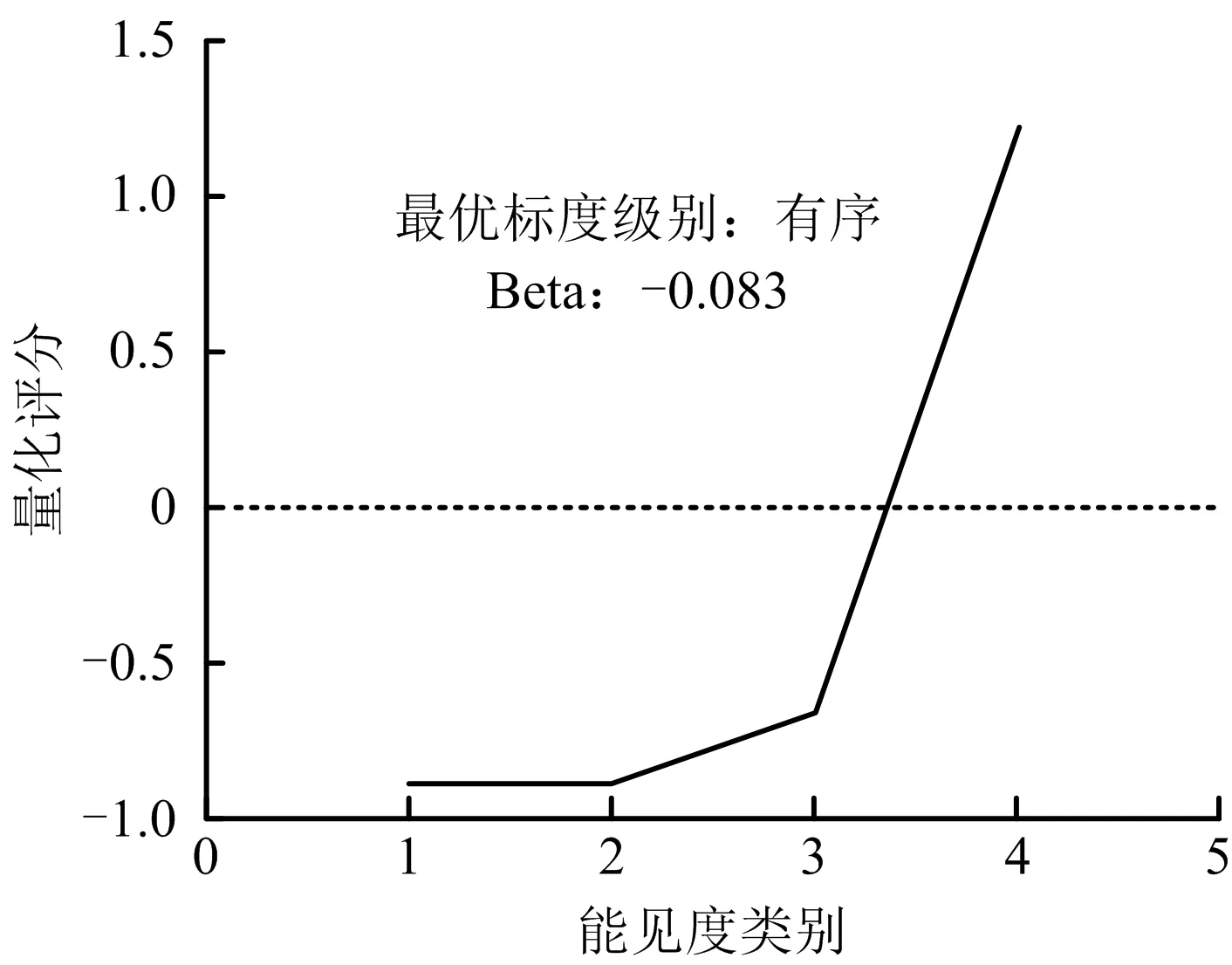
图2 能见度量化评分Fig.2 Quantitative scoring of visibility
综上,在道路横断面位置、中央隔离设施、路侧设施防护类型等8个变量之间不存在共线性问题,但路面状态这一变量未通过显著性检验,选择剔除,把剩余变量的标准化数据(即量化评分)代入回归方程,最终可得到发生某种事故形态的偏向情况,方程如式(2):
(2)
3 无序多分类Logit模型
3.1 模型构建
Logit模型主要研究的是因变量与自变量的依存关系,其要求因变量取值为分类变量(二分类或多分类),自变量可为连续变量、等级变量、分类变量。在实际问题中,有很多变量并非为连续性变量、等级变量,如事故形态种类为无序性分类变量,故选用无序多分类Logit回归模型。该模型首先定义因变量的某1个水平为参照水平(SPSS默认取值水平大的为参照水平),本文以刮擦碰撞(Y4)的事故形态为对照组,分析追尾碰撞(Y1)、正面碰撞(Y2)、侧面碰撞(Y4)3类事故形态的相对发生概率,构建3个广义Logit模型,如式(3)~(5):
(3)
(4)
(5)
式中:Pr表示第r种事故形态的发生概率,其中r=1,2,3,4;α1~α3为回归截距,为了避免模型误设;βij为模型的回归系数,其代表了自变量对新变量的影响程度,绝对值越大,表示影响程度越大,反之则越小;Xij为第i种自变量的第j种指标取值,其中i∈[1,7],j∈[1,9]且均为正整数。
如图1所示。以第4个因变量为参照水平,如果需要比较正面碰撞和侧面碰撞(2和3),则直接将式(4)和式(5)相减即可得到相应函数[13-14]。无序多分类Logit模型中参数标定方法可以采用极大似然法估计参数[15]。给定样本的数据量越大,通过这种方法估计参数的误差越小,其估计结果方差也越小。基本步骤为:
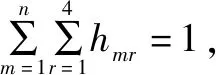

(6)
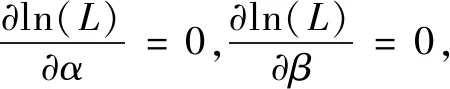
3.2 模型拟合度检验
利用拟合优度检验和似然比检验,对Logit模型的拟合效果进行评价。拟合优度检验法主要是为验证模型的正确率和有效性,其基本思路是依据总体分布状况,计算分类变量中各类别的期望频数,与分布的观测频数进行对比,判断期望频数与观察频数是否有显著差异,从而达到对分类变量分析的目的。似然比检验用来评估模型是否具有统计学意义,对仅包含常数项(截距)模型和包含路侧设施防护类型、中央隔离设施等7个自变量的模型拟合效果进行评估。
根据模型拟合度检验原理及方法,得出具体拟合度检验值见表3。皮尔逊卡方sig.值为1.000>0.050,说明模型对原始数据的拟合良好,模型有效。似然比检验中sig.值小于0.001,说明至少有1个自变量的偏回归系数不为0,即包含7个自变量的模型的拟合优度好于仅截距的无效模型。

表3 拟合检验结果Table 3 Fitting test results
3.3 模型结果分析
3.3.1 追尾碰撞致因分析
追尾碰撞事故形态致因分析模型见表4,表中β为回归系数,Exp(β)作为效应指标分析自变量的各个分类对因变量影响程度的大小,当β>0,Exp(β)>1说明了变量为危险因素;当β<0,Exp(β)<1说明了变量为保护性因素;当β=0,即Exp(β)=1说明该因素与因变量无关[16]。P值用来判定假设检验结果,当P大于一般规定的临界值0.05,在统计学上没有意义,模型在运算迭代过程中,直接将它们剔除;当P<0.05时,在统计学上有意义。
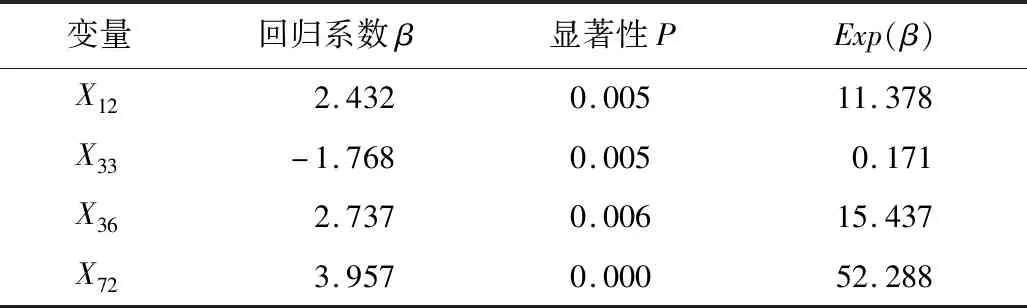
表4 追尾碰撞事故模型参数汇总Table 4 Summary on model parameters of rear end collision accident
由表4可得追尾碰撞事故拟合模型如式(7):
(7)
式中:Xij取值为0或1,i∈[1,7],j∈[1,9]且均为正整数。
分析表明,路侧设置绿化带回归系数小于0,对追尾碰撞事故有负向影响,为事故发生的保护性因素,相对于路侧无防护时发生追尾碰撞事故概率的0.171倍;而路侧设置金属护栏时回归系数大于0,是事故发生的危险因子,增大了车辆发生追尾碰撞的概率。同样在道路横断面位置为非机动车道回归系数大于0,是机动车道发生事故概率的11.378倍。夜间行车时,无照明是事故发生的危险因子,车辆发生追尾碰撞事故概率是有照明的52.288倍。
3.3.2 正面碰撞致因分析
正面碰撞事故形态致因分析模型见表5,模型构建方法同3.3.1节。
由表5可得正面碰撞事故拟合模型如式(8):
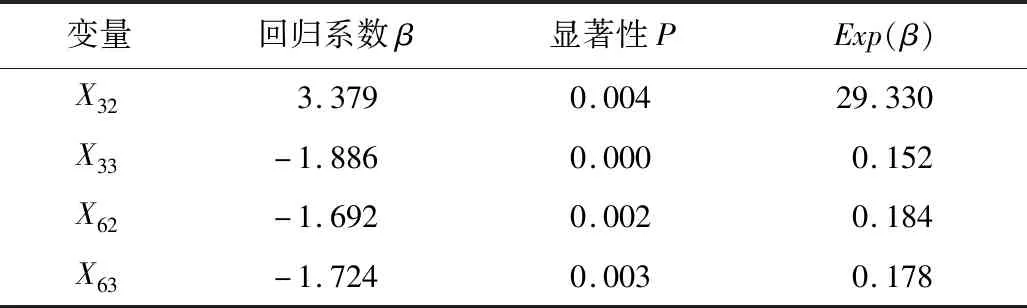
表5 正面碰撞事故模型参数汇总Table 5 Summary on model parameters of frontal collision accident
(8)
分析表明,路侧设置行道树时回归系数大于0,是事故发生的危险因子,增大了车辆发生正面碰撞的可能性,发生事故概率是路侧无防护时的29.330倍;路侧设置绿化带回归系数小于0,对正面碰撞事故有负向影响,为事故发生的保护性因素,相对于路侧无防护时发生追尾碰撞事故概率的0.152倍。
模型中能见度为50 m≤X62<100 m和100 m≤X63<200 m的回归系数均小于0,是正面碰撞事故的保护性因素,是能见度X64≥200 m时发生事故的0.184倍和0.178倍。
3.3.3 侧面碰撞致因分析
侧面碰撞事故形态致因分析模型见表6,模型构建方法同3.3.1节。
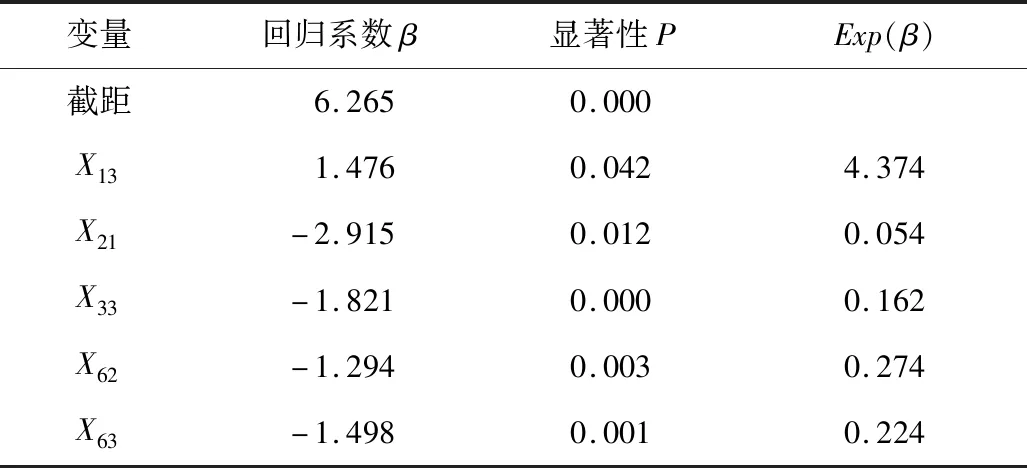
表6 侧面碰撞事故模型参数汇总Table 6 Summary on model parameters of side collision accident
由表6可得侧面碰撞事故拟合模型如式(9):
(9)
分析表明,在机非混合道同样容易发生侧面碰撞,且是机动车道的4.374倍。中央隔离设置绿化带小于0,是事故发生的保护性因素,以隔离墩为参照,影响程度是设置隔离墩设施的0.054倍。且具有路侧设施绿化带的道路发生侧面碰撞事故概率是不具有此类型设施的0.162倍。
模型表明侧面碰撞也与能见度有显著的相关关系,相对于能见度X64≥200 m,在能见度为50 m≤X62<100 m和100 m≤X63<200 m范围内车辆发生侧面碰撞事故的概率降低了约70%。
综上,路侧设置绿化带是碰撞事故中的重要影响因子,事故率约是无防护的15%,另外中央隔离设施使用绿化带也可有效降低侧面碰撞事故率,故在道路环境允许的情况下可以尽量多设置绿化带;路侧行道树设置不合理或未及时修剪,使车辆不能有效识别道路信息,是正面碰撞的重要影响因素,事故概率不具备此类设施的29.330倍,故应对绿化设施位置进行修正;夜间在没有路灯的路段行车会增加危险性,发生追尾碰撞事故的概率是有照明的52.288倍,因此,在道路上要合理的为夜间车辆和行人出行提供必要的照明设施;目前城市各道路宽度较窄,无法达到机非分开,该市车流量较大,故在机非混合道上行驶的车辆容易发生碰撞事故,且事故率是机动车道的4.374倍,对于碰撞事故多发性道路若条件允许应该尽量减少对机非混合道的设置;能见度为50 m≤X62<100 m和100 m≤X63<200 m时事故率较低,这也从侧面反映了驾驶员在能见度降低时对车速的调控以及自我意识的提高。
3.3.4 模型验证
上述模型由某市的交通事故数据构建而成,尽管通过了统计学相关检验,模型拟合度较好,但其是否能表征该市的事故特征机理,仍需对模型进行验证。抽取该市2017年1月到2019年12月另外100起交通事故数据形成验证样本集合,按照上述建模方法,将相关影响指标代入式(7)~(9)。计算结果见表7。
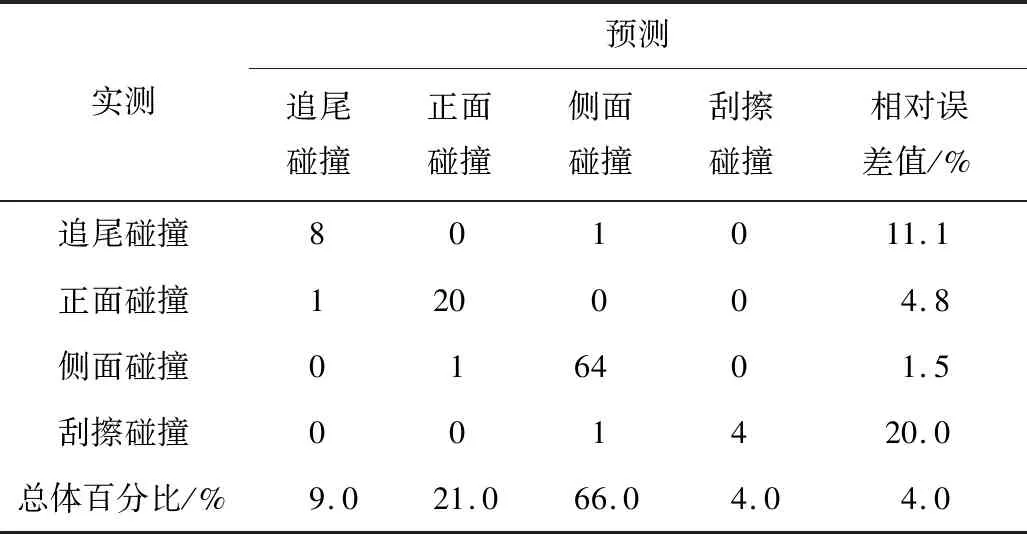
表7 模型精度Table 7 Model accuracy
由表7可知,模型整体相对误差仅为4.0%,各事故形态的相对误差分别为11.1%,4.8%,1.5%,20.0%,平均相对误差为9.4%,这说明模型适用性较好。
4 结论
1)基于最优尺度分析方法判断各因素之间是否存在共线性的问题以及是否具有统计学意义,将具有统计学意义的影响因素与事故形态纳入无序多分类Logit模型,有效识别影响事故形态的各项因素,并通过模型中回归系数与优势比值得到各因素对事故形态贡献水平,便于分析事故形态致因。该方法用于某特定道路或地区交通事故研究,有助于揭示道路建设的潜在危险因子,同时由于数据是按照事故形态分组,模型结果可以辅助事故黑点筛查和预测,并作为道路安全管理部门改善的参考,具有一定的现实意义。
2)模型表明,路侧、中央隔离设施设置绿化带,增加必要的照明设施,有望降低事故发生率,这一点对于城市道路改造具有实际意义;路侧行道树设置不合理或未及时修剪,使车辆不能有效识别道路信息,是正面碰撞的重要影响因素,故该市应对绿化设施位置进行修正;机非混合道是事故的危险因子,增大了侧面碰撞事故发生概率,道路条件允许的情况下可以尽量实行机非分行。
3)文中研究尚存在不足之处,首先,在交通事故形态对照组设置方面,本文仅以刮擦碰撞作为对照组进行分析,后续可调整因变量的分类形式,获得对比较为明显的因变量分类作为对照组;其次,自变量对照组的选择,虽然能得到一些有意义的结果,但应该在后续研究中设置对比较为明显的分类作为对照类;在自变量选择方面,未来也会将交通量、事故车型等信息考虑在内。

