基于多因素的LSTM瓦斯浓度预测模型*
刘 莹,杨超宇
(安徽理工大学 经济与管理学院,安徽 淮南 232001)
0 引言
煤矿井下开采地质条件复杂。采矿过程中,在煤体地应力和煤层瓦斯压力的作用下,煤矿可能会出现煤层瓦斯向矿井采掘空间喷出的现象[1-4],某些征兆现象的难以察觉易使井下丧失事故最佳防范期[5]。
在煤矿瓦斯涌出量预测方面,学者们提出了许多算法模型,如随机森林[6]、回归树[7]、支持向量机(SVM)算法[8]、神经网络算法[9]、多元线性回归[10]等。郭瑞等[11]提出利用信息融合技术和遗传支持向量机(GA-SVM)相结合的算法,该算法使用遗传算法(GA)的全局优化能力对支持向量机(SVM)进行参数和特征向量的最佳组合查找,以达到对SVM优化的目的;李超群等[12]基于集成学习的思想,采用将SVM与模型树(Model Tree)相结合的方法,并利用交叉验证法对模型进行训练和验证,获得更具泛化能力和预测准确性的瓦斯浓度预测模型。为解决经典CART回归算法泛化性能差、易过拟合的缺陷,刘鹏等[13]利用SVM在回归树的叶节点部分进行建模的方式,建立瓦斯涌出量的预测量化模型,该方法不但防止过拟合的发生,同时提高模型稳定性、预测精度;刘晓悦等[14]在云计算的基础上运用Elman神经网络算法构建瓦斯浓度预测模型,通过遗传算法优化Elman神经网络,并以该模型对海量数据进行训练,该模型能够在短期预测煤矿瓦斯浓度方面保证高效性,同时也确保了预测精度;张震等[15]在瓦斯历史数据的基础上,将LSTM算法应用到矿井瓦斯浓度预测,该方法的瓦斯浓度预测曲线能够高度吻合监测数据曲线,但是,模型只考虑了瓦斯历史数据,忽略了其他井下环境因素对瓦斯浓度变化的影响。
由此可见,在瓦斯预测领域,瓦斯浓度预测方法多为单因素分析,并没有考虑在当前时间和空间中的其他环境影响因素。LSTM模型的应用只根据单因素预测,且大都应用在小样本范围。本文提出基于多因素的LSTM瓦斯浓度预测模型,在融合井下多源监测大数据的基础上,通过巷道风速、井下温度、井下CO浓度、历史瓦斯浓度数据分析出影响瓦斯浓度变化和未来趋势的特征,挖掘出多源监测数据中的时间特征和空间因素特征,多步预测未来瓦斯浓度趋势。
1 LSTM网络模型
长短期记忆(Long short-term memory,LSTM)网络在处理序列数据时,能够避免RNN的梯度爆炸和梯度消失问题。LSTM的关键在于神经单元的信息状态,神经单元的信息流传通过3个逻辑门(遗忘门、输入门、输出门)控制,LSTM的网络结构如图1所示。

图1 LSTM网络结构Fig.1 LSTM network structure
LSTM网络的信息处理过程可用式(1)~(6)表达:
ft=σ(Wf·[ht-1,xt]+bf)
(1)
it=σ(Wi·[ht-1,xt]+bi)
(2)
(3)
(4)
ot=σ(Wo·[ht-1,xt]+bo)
(5)
ht=ot·tanh(Ct)
(6)

2 基于多因素的LSTM瓦斯浓度预测模型构建
基于多因素的LSTM瓦斯浓度预测模型的构建主要包括6个模块:获取数据、多源数据预处理、特征工程、模型的构建、模型的训练和优化、模型的预测。
模型首先从数据库中获取井下CO浓度、温度、风速、瓦斯浓度的井下传感器数据,将数据按照数据产生时刻进行数据融合,构成完整的样本数据。其次,将数据中的异常值、缺失值、调校值等进行数据预处理。然后,将样本数据经过特征工程处理,如:特征衍生、时间序列数据监督化、无量纲化,使得样本特征维度增加,同时将时间序列数据集转化为机器学习的有监督学习任务的数据集。接着,通过经验法和逐步试错法确定LSTM网络的隐藏层神经元的数目以及其他各个参数。最后,模型进行训练、验证和测试,并且预测瓦斯浓度。基于多因素的LSTM瓦斯浓度预测模型的主要构建流程如图2所示。
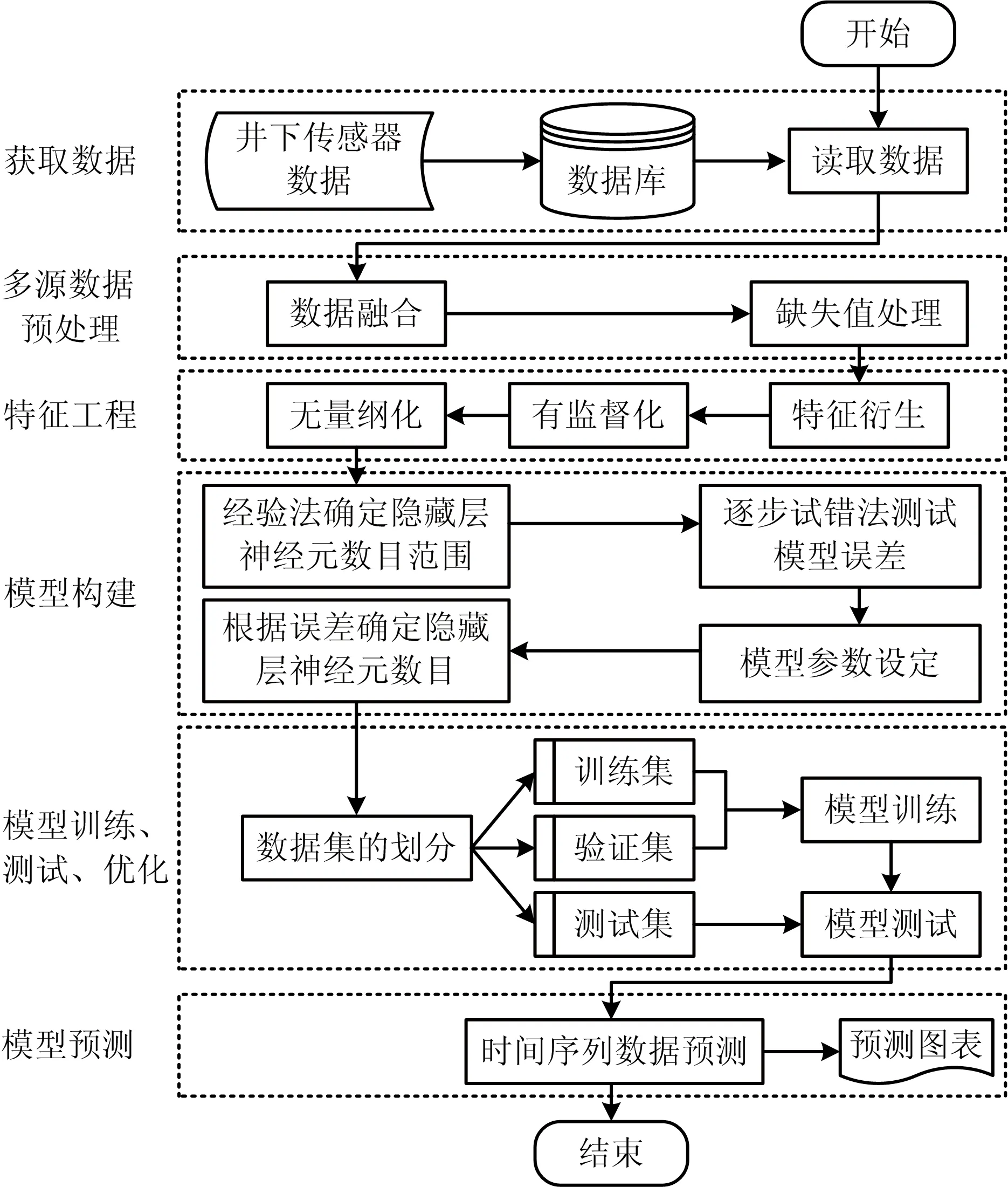
图2 模型流程Fig.2 Model flow chart
2.1 多源监测数据预处理
1)数据融合:煤矿井下传感器类型多、数量大,每个传感器每天产生大量的数据。因此,对井下监测数据进行分类、整理、选择,以及多源数据的融合是使井下监测数据产生价值的前提。本文选择井下CO浓度、温度、风速、瓦斯浓度的传感器数据,对其整理、融合,构成完整的数据样本。
2)缺失值处理:瓦斯监测数据中存在大量的缺失数据,倘若将存在缺失值的样本删除,将会破坏时间序列数据的序列性、数据平稳性,还会由于数据样本过小而导致模型训练不足,最终导致预测效果差的现象。本模型采用缺失数据向前补齐的方法,用前1个非缺失值去填充该缺失值。
2.2 模型数据特征分析
1)特征衍生:由于原始的瓦斯监控数据中,样本数据特征数量较少,且多为低效特征。为了最大限度提取瓦斯监控数据中的特征信息以供LSTM算法训练模型,采用特征多项式融合法衍生新特征。特征多项式融合法不但可以得到交叉项特征,还可以得到高次项特征。多项式特征的衍生将低维特征进行组合,得到高维特征,使得LSTM模型更大程度地捕捉数据的基本关系,“学习”更多的数据信息。特征衍生表达式如式(7)~(8)。
(7)
(8)
式中:Poly()n为n阶特征衍生;a,b,c为数据集的3个特征;Numnew为新衍生的特征数量。
本文中,原始数据特征数量为3,经过三阶多项式增项后,得到的特征数量为19,其中新特征数目为16。
2)有监督化:由于瓦斯浓度受多个环境因素影响,且通过历史数据的变化趋势预测未来的发展,因此,为了充分考虑影响瓦斯浓度的时空特性,将一定滞后期的瓦斯浓度数据作为新的特征信息,使模型将数据的时间性特征和空间因素特征充分学习。同时,将样本的时间序列数据组合成成对的输入输出格式,将时间序列预测问题转化为监督学习问题。
本文将滞后期为20的瓦斯浓度作为t时刻的时间性特征,与3个环境因素特征经特征衍生后得到的19个特征共同构成模型的特征,处理后的样本数据,见表1。表1中的3个样本数据均由39个特征数据和1个对应的实测瓦斯浓度(jw)数据组成。

表1 处理后的样本数据示例Table 1 Examples of sample data after processing
3)无量纲化:由于数据中涉及多个可能影响瓦斯浓度的指标,每个指标的数值范围不同。为了统一指标数值对模型产生的影响,本文使用数据归一化的方法对样本数据无量纲化,归一化数学表达如式(9):
(9)
式中:x为某个指标特征无量纲化前的数据值;max,min分别为该指标在所有样本中的最大值、最小值;x′为该指标无量纲化后的数据值。
2.3 样本数据集划分
样本数据在输入模型之前,需要将数据分割为训练数据集、验证数据集、测试数据集。为了保持时间序列数据的时间相关性,数据分割时不能采用随机分割的方式。本文将2个数据分割点插入瓦斯浓度时间序列数据,第1个分割点前的序列样本数据作为训练集,第1个分割点和第2分割点间的样本数据作为验证集,第2分割点后的数据作为测试集。
2.4 LSTM模型构建
本文基于多因素的LSTM瓦斯浓度预测模型的实现基于python语言的keras库完成。LSTM模型的结构主要分为3部分:数据输入层、隐藏层、结果输出层。LSTM模型的隐藏层数目为1,隐藏层神经元个数通过逐步试错法进行确定,输出层神经元个数为1。模型输入数据结构为(1,39),其循环层间断开神经元的比例设置为0.6,模型优化器选用Adam,完成模型的自适应学习率的参数更新过程。模型损失函数选用平均绝对误差MAE(Mean Absolute Error),计算瓦斯浓度预测值距离真实值的偏差。模型训练的epochs为200轮,batch_size为72,其余参数采用默认参数。
本文借鉴文献[15]中的经验法计算出隐藏层神经元的数量,在经验法确定神经元数量范围的基础上,采用逐步试错法选择模型的最小均方根误差,从而确定预测模型的隐藏层神经元数量。确定隐藏层神经元数目范围的经验计算公式如式(10):
(10)
式中:a,b为神经网络模型数据输入层、结果输出层的神经元数量;c为整数,取值范围为1~10;q为根据公式计算确定的隐藏层神经元数量。
基于多因素的LSTM瓦斯浓度预测模型的预测性能指标选用均方根误差RMSE(Root Mean Squard Error)和MAE,RMSE和MAE的公式如式(11)和(12):
(11)
(12)

3 实验与分析
实验数据来自贵州省某煤矿的10901工作面的2021年1月14日10时49分至2021年4月9日19时26分的井下CO浓度、风速、温度、瓦斯浓度监测数据,样本数据量为103 779条。井下监测数据经过数据融合、数据预处理和特征工程后,得到样本条数为102 759条,其中训练集样本大小为99 650条,验证集样本大小为2 034条,测试集样本为1 075条。
LSTM模型设计的重要步骤是隐藏层节点数目的确定,本文根据公式(10)计算LSTM模型的隐藏层神经元数量。当前数据输入层神经元数目为39,结果输出层神经元数目为1,则LSTM隐藏层神经元的数量可取范围为7~17。使用逐步试错法确定LSTM隐藏层神经元数量。基于多因素的LSTM瓦斯浓度预测模型在不同隐藏层神经元数目下的模型测试误差如图3所示。

图3 不同神经元数量下的模型误差Fig.3 Diagram of model errors under different numbers of neuron
由图3可得:当隐藏层神经元数目为15时,RMSE为0.021,MAE为0.01,模型综合误差最小。因此,基于多因素的LSTM瓦斯浓度预测模型的隐藏层神经元数目确定为15。
3.1 模型预测性能
为了对比LSTM单变量预测模型、RNN预测模型与基于多因素的LSTM瓦斯浓度预测模型的瓦斯浓度预测性能,使用相同的数据集,对这3个模型进行瓦斯浓度预测实验。实验采取控制变量法,模型取滞后期为20的瓦斯浓度数据作为时间特征。使用测试样本集进行预测效果的对比,图4为利用相同井下传感器监控数据进行RNN模型、LSTM单变量模型、基于多因素的LSTM瓦斯浓度预测模型进行预测的效果图。其中,LSTM单变量模型、基于多因素的LSTM瓦斯浓度预测模型的隐藏层神经元数目均为15。由于测试集样本数量较大,将前200条样本数据进行对比。

图4 不同模型的瓦斯预测效果Fig.4 Gas prediction effect of different models
表2为模型预测的误差和模型训练及预测所耗时。
由图4和表2可知:在不同模型预测过程中,RNN模型耗时最短,其次是LSTM单变量模型,最后是LSTM多因素模型;但是在模型预测的RMSE,MAE误差上,LSTM多因素模型预测误差最小,其次是LSTM单变量模型,最后是RNN模型。虽然LSTM多因素模型在模型训练时耗时更长,但是模型的预测准确性更高。

表2 模型预测性能对比Table 2 Comparison of model prediction performance
3.2 长期、短期瓦斯浓度预测
长期瓦斯浓度预测中,取间隔期为20个序列点前的滞后期数据;短期预测取最近的滞后期数据,长期和短期瓦斯预测滞后期均为10,20,30,40,50,60。长期和短期的瓦斯浓度预测RMSE,MAE如图5所示。从总体上看,短期预测中,LSTM多因素模型的瓦斯浓度预测误差在RMSE和MAE的误差均为最小。在短期预测时,滞后期为10和60时,LSTM单变量和多因素预测结果不相上下,但是在长期预测过程中,LSTM多因素预测误差均远小于LSTM单变量和RNN,说明LSTM多因素预测模型在长期预测中更有优势。

图5 不同时间间隔预测Fig.5 Prediction under different time intervals
4 结论
1)通过融合多源监测数据,为模型提供了多个影响瓦斯浓度变化的环境因素,结合LSTM网络模型,高效地预测未来瓦斯浓度的变化趋势。
2)利用特征多项式衍生新特征,将环境因素特征和历史瓦斯浓度时间性特征相结合,产生交叉项特征和高次项特征,使得模型充分挖掘监控数据中的信息。
3)将瓦斯浓度时间序列预测问题转化为监督学习,既避免了人工标注成本,又通过机器学习找到特征和标签之间的更多隐藏联系,使模型充分挖掘数据中的信息,提高模型的预测性能。
4)与LSTM单变量模型、RNN模型相比,基于多因素的LSTM瓦斯浓度预测模型在瓦斯浓度长期预测中更具优势。

