考虑人员伤亡的高校宿舍火灾风险评估方法研究*

于洪霞，张英华，秦挺鑫，王晶晶，张 益，高玉坤

(1.北京科技大学 金属矿山高效开采与安全教育部重点实验室，北京 100083；2.北京科技大学 矿山避险技术研究中心，北京 100083；3.中国标准化研究院，北京 100191；4.北京城市系统工程研究中心，北京 100044)

0 引言

随着社会经济发展，建筑物数量和人口密度不断增长，往往随之而来的是火灾风险不断增大，给人民生命和财产造成一定威胁。高校宿舍楼作为高校不可或缺的建筑，建立时间普遍较早，存在电气线路老化、部分消防设施缺失和消防通道狭窄等火灾安全隐患。同时，宿舍楼是学生学习生活的最主要场所，一旦发生火灾，火势增长速度较快，又因宿舍楼内学生数量较多，在进行火灾疏散时易发生拥挤，不仅影响疏散速度，还可能造成踩踏等二次事故。宿舍楼火灾发生可能性较高，且火灾发生后可能造成大量人员伤亡。因此，高校应该建立科学的宿舍楼火灾风险评价机制，以遏制火灾事故的发生，降低火灾事故损失。

部分学者针对火灾风险评估开展研究：范维澄[1]采用火灾双重性理论构建火灾评估体系；易立新[2]采用事故树分析法，结合随机过程的马尔克夫模型，建立火灾风险评价动态模型；杜红兵等[3]采用模糊数学原理，借助系统工程的模糊综合评价法，对高层建筑的火灾风险进行评估。

综上，我国火灾风险仍集中在定性和半定量分析。据文献统计，我国近年来核心期刊综述和定性分析占37.8%，半定量占61%，定量分析只占1.2%[4]，但定性和半定量分析结论存在较大主观性，缺乏定量化数据支撑，导致结论不具有说服力。因此，本文通过构建建筑火灾伤亡人数函数模型，得到不同火灾场景下的伤亡人数，对火灾风险评估方法的进一步完善具有参考借鉴意义。

1 ASET概率密度函数模型构建

1.1 ASET的不确定性分析

ASET的大小不仅由火灾位置、火灾增长模型和热释放速度等火灾因素决定，还受建筑内消防系统的影响。例如由于可燃物的不确定性，建筑内火灾增长系数是1个随对数正态分布的随机变量[5]。此外，还有许多其他不确定因素，如烟雾报警器的报警时间、机械排烟风扇的启动时间和喷淋系统的启动时间等，这些因素都可能影响建筑火灾临界时间。因此，可以通过概率分布描述ASET以表示其不确定性。

1.2 ASET概率密度函数简化

从文献[6]得出ASET的概率密度函数呈正态分布，但正态分布的函数需要确定多种参数，要想通过拟合函数曲线得到函数表达式需经过大量计算或模拟。将ASET的概率密度函数简化为三角分布模型，可通过确定概率密度函数的最小值、最大值和最可能值建立ASET概率密度函模型。ASET三角分布的概率密度函数如式(1)所示：

(1)

式中：t为火灾发生时间，s；a为达到火灾临界状态的最短时间，即达到ASET的最短时间，s；b为达到ASET的最长时间，s；c为达到ASET时，可能性最大的时间，s。

根据式(1)可得，ASET概率密度函数的确定应获得在对应火灾场景下ASET的最小值a、最大值b及最可能值c。

2 宿舍楼火灾仿真模拟

2.1 宿舍楼描述及模型建立

某高校宿舍楼平面呈L型，东西长72 m，南北长92 m，走廊宽度2.8 m。该宿舍楼共有12层，每层有41间宿舍，宿舍长宽高为6 m×3.5 m×3.2 m，宿舍门的尺寸为1 m×2.1 m，宿舍楼平面示意如图1所示。R是宿舍楼每层的排烟前室；D表示宿舍楼的防火门；S1、S2和S3分别代表宿舍楼内的3个防烟楼梯间；V1和V2分别代表了宿舍楼每层的2个排烟口。宿舍楼每层布局基本相同，每层均为1个独立的防火分区，宿舍楼的防烟楼梯间内无可燃物，所以只对宿舍楼的某1层展开研究。

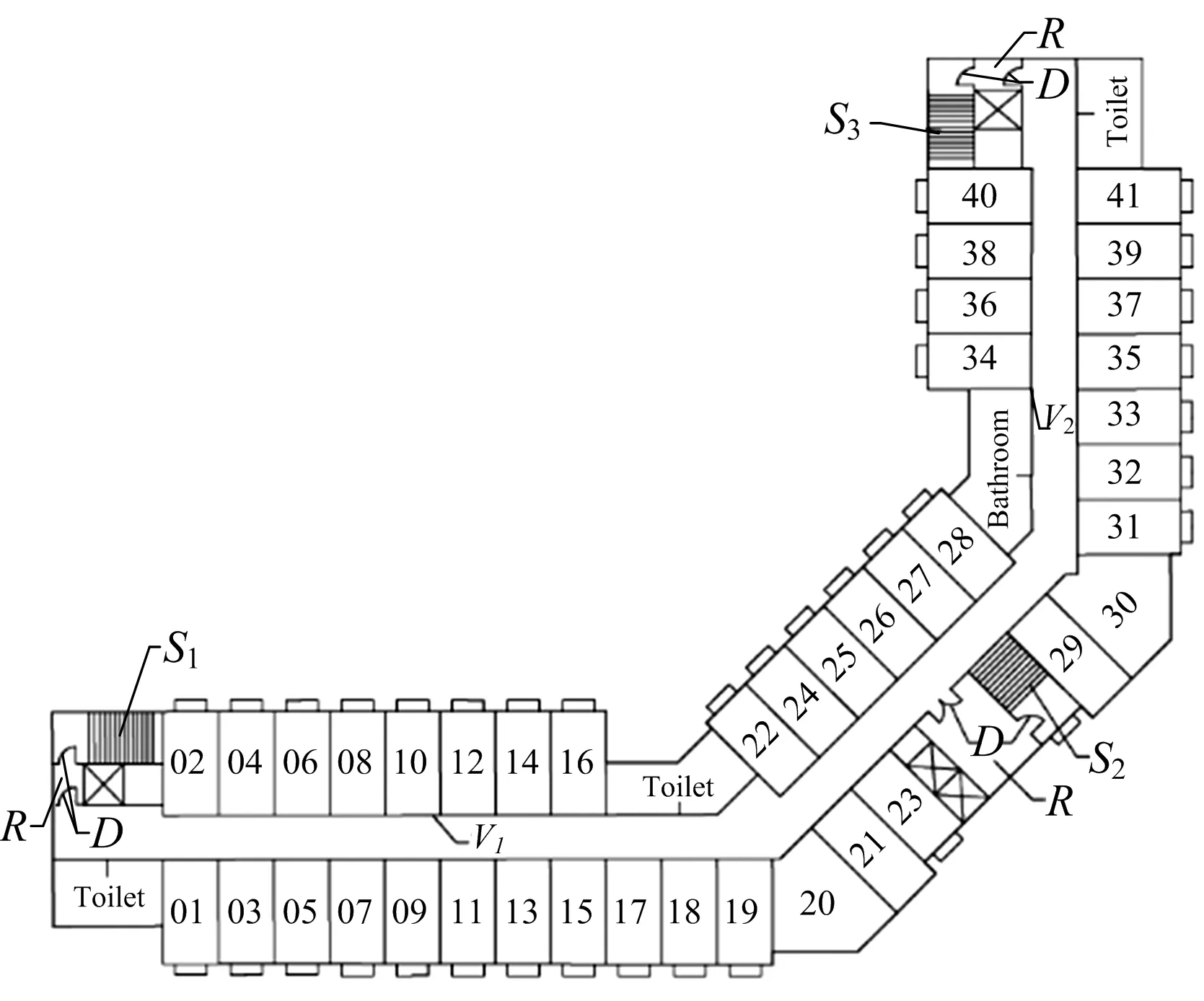
图1 宿舍楼平面示意Fig.1 Schematic diagram of dormitory building plan

利用FDS前处理软件PyroSim 2016软件对宿舍楼楼层平面进行3D物理建模，进行网络和区域划分。计算空间均匀划分为0.5 m×0.5 m×0.5 m的网格，共127 680个，宿舍楼层平面PyroSim模型如图2所示。

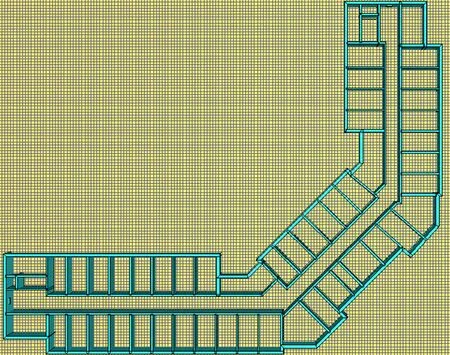
图2 宿舍楼层平面PyroSim模型Fig.2 PyroSim model of dormitory building floor plan

2.2 参数设定

1)火灾模型和火灾规模。火灾的发展是1个不断加速的过程，选择t2火灾模型[7]；火灾增长系数的最小值、最大值和最可能值分别为0.027，0.101，0.046 89 kW/s2[8-9]；根据建筑火灾热释放速率标准[10]，模拟的最大热释放速率取6 MW。

2)模拟时间。根据疏散模拟分析，宿舍楼内人员在600 s内一定能够完成每层的疏散，因此将火灾模拟时间设定为600 s。

2.3 火灾场景设置

火源设定为位于西侧的01号房间和位于中部的26号房间，宿舍火灾原因设定为由于学生吸烟点燃床铺，点火源大小设定为直径为10 mm的粒子，温度为350 ℃，点燃速度为立即点燃，床铺材料设定为布和聚氨酯。机械排烟系统分为正常和故障2种状态，分别设置火灾场景1、2、3、4，见表1。每种火灾场景需要在3种不同的火灾增长系数下进行模拟，一共需要12次火灾模拟。

表1 宿舍楼火灾场景设定Table 1 Setting of fire scenes in dormitory building

此外，模型中加入温度、CO体积分数和能见度的切片，监测点设置在起火房间、走廊及楼梯间处，每个监测点布置高度为1.7 m。走廊中心线水平方向共布置9个监测点，第1个监测点位置正对起火房间的门，由此沿着走廊方向每隔2个房间布置1个监测点。

2.4 火灾模拟结果分析

1)当火灾增长系数取最大值0.101 kW/s2时，火灾场景1能见度临界时间为283 s，温度临界时间为352 s，CO浓度在模拟600 s内未能达到临界值，ASET取3个临界时间中的最小值，为283 s。火灾增长系数取最小值、最可能值及火灾场景2、3、4模拟结果均显示能见度临界时间相对最短，其次为温度，CO浓度未达到临界值。由此可见，能见度对可用疏散时间的影响相对最大，温度影响次之，CO浓度影响相对最小。

2)当火灾增长系数取最大值0.101 kW/s2时，火灾场景1的能见度和温度的临界时间分别为283，352 s，火灾场景2的值为211，307 s，火灾场景2对应临界时间值均小于场景1。且火灾发生后相同时间内，场景2的CO浓度要明显大于场景1。同样，火灾场景4的能见度和温度的临界时间均小于场景3，均说明宿舍楼机械排烟的开启，能有效增加影响疏散参数的临界时间，使ASET变大，有利于人员进行安全疏散。

3)当火灾增长系数取最大值0.101 kW/s2时，火灾场景3的能见度和温度的临界时间分别为201，253 s，火灾场景3的对应临界时间值均小于场景1。同样，火灾场景4的能见度和温度的临界时间均小于场景2，均说明当宿舍楼层中部发生火灾时，火灾烟气蔓延速度比宿舍楼层两侧发生火灾时更快，所以可用疏散时间更短，不利于人员的安全疏散。

4)当火灾增长系数取最小值0.027 kW/s2和最可能值0.046 89 kW/s2时，上述结论均适用。

2.5 ASET概率密度函数的确定

根据不同火灾场景下的ASET数值得到ASET概率密度分布函数参数，见表2。

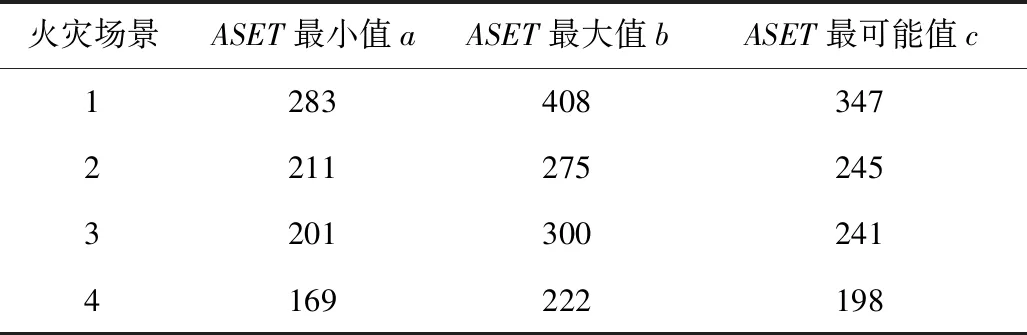
表2 ASET概率密度分布函数参数Table 2 Parameters of ASET probability density distribution function s

将ASET概率密度分布函数参数带入式(1)，得到各个火灾场景ASET三角分布的概率密度函数。

3 宿舍楼人员疏散仿真模拟

3.1 疏散参数设置

1)火灾必须安全疏散时间RSET。人员的必须疏散时间[11]由火灾探测时间、报警时间、人员预运动时间和人员运动时间4部分组成。

参考相关文献，火灾探测报警系统正常时，火灾报警时间设置为60 s；当火灾探测报警系统故障时，将人员发现火灾时间设置为90 s；将人员发现火灾失败的火灾探测报警时间设置为120 s[12]。

根据文献[13]可知，当宿舍楼内人员处于清醒状态时，预运动平均时间设定为60 s；人员处于睡眠状态时，预运动的平均时间设定为120 s。

2)疏散人数。对于不同时间，宿舍内的人员数量不同。根据实际调查，将上课时间段每个宿舍设定2人，午晚休及深夜睡觉时间每个宿舍设定为全员5人，每层共41间宿舍，分别为82，205人。

3)疏散路线。由于该宿舍楼每年都会进行多次火灾疏散演练，外加宿舍内学生对宿舍建筑构造较为熟悉，设定火灾发生后，房间内学生会按最近疏散出口进行疏散，人员疏散至防烟楼梯间时，认为人员已疏散至安全区域，完成疏散。

4)疏散速度。根据最大疏散速度实验测定，疏散模拟中男生的最大疏散速度设定为在1.55～1.75 m/s均匀分布，女生最大疏散速度设定为在1.45～1.60 m/s均匀分布。

5)身高和最大肩宽设定。参考国家体育总局发布的《2014年国民体质监测公报》的数据，疏散中18～25岁的男生和女生的平均身高设定为171.9，159.9 cm。疏散模拟的最大肩宽参考文献[14]中对于男女青年的测量结果，男性最大肩宽取(47.66±5)cm，女性最大肩宽取(42.356±5)cm。

3.2 疏散场景设置

根据火灾发生时间段和火灾探测方式的区别，宿舍楼火灾疏散可分为6个疏散场景，见表3。由于男生和女生身高和最大肩宽等参数不同，所以还需要针对不同性别进行疏散，共需要进行12次疏散模拟。

表3 宿舍楼疏散场景Table 3 Evacuation scenes of dormitory building

3.3 Pathfinder疏散模型的建立

根据宿舍楼平面模型建立的宿舍楼Pathfinder疏散模型如图3所示。人员随机分布于宿舍房间中的各个位置中，结合实际情况选择Steering模式[15]进行人员疏散模拟。

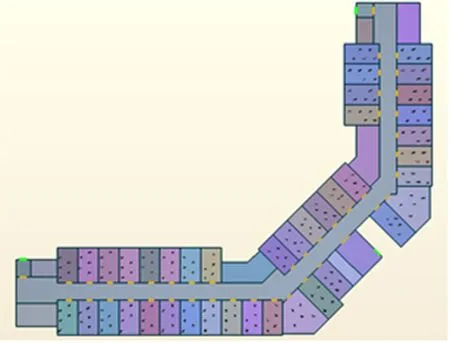
图3 宿舍楼Pathfinder疏散模型Fig.3 Pathfinder evacuation model of dormitory building

3.4 疏散模拟结果与分析

由模拟可得各个疏散场景下男生和女生所用疏散时间及由未疏散人数与时间曲线的线性拟合函数，见表4。

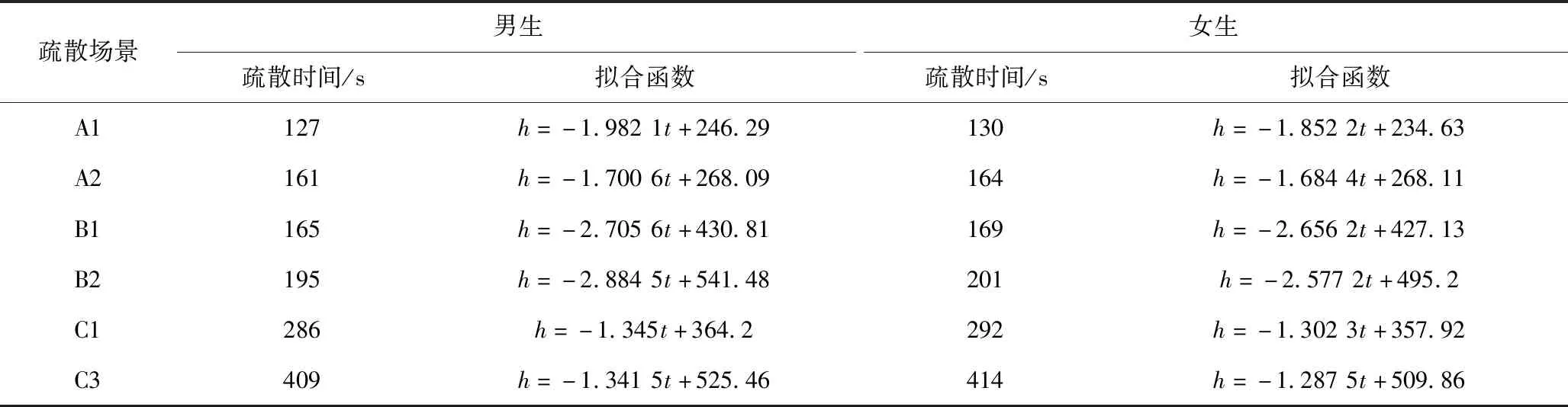
表4 宿舍楼疏散时间及拟合函数Table 4 Evacuation time of dormitory building and fitting functions

1)结果显示，在A1场景下，男生在127 s内完成全部82人的疏散，女生需要130 s完成所有人的疏散，且男生的未疏散人数与时间曲线的线性拟合函数的斜率为-1.982 1，女生的线性拟合函数的斜率为-1.852 2，男生的拟合函数斜率略大于女生。同样，其他5个场景均符合上述规律，说明男生的疏散时间稍短于女生，疏散效率要略高于女生。

2)在A2场景下，宿舍楼内82名男生全部疏散用时为161 s，82名女生全部疏散用时164 s，对比A1和A2场景下对应人员疏散时间和线性拟合函数斜率可知，A1场景下人员疏散时间更短且疏散效率更高，对比B1和B2场景的数据均符合上述规律。因此，在相同条件下，火灾探测报警成功比人员发现火灾成功的必需安全疏散时间更短，疏散效率更高。

3)通过将疏散场景A1和B1，以及场景A2和B2进行对比，场景B1和B2男生、女生的疏散时间均大于场景A1和A2，但场景B1和B2男生、女生未疏散人数与时间曲线的线性拟合函数的斜率均大于场景A1和A2。

说明当火灾探测方式相同时，宿舍楼内人员越多，所有人员的必须安全疏散时间越长；上课期间由于宿舍楼内人员较少，对疏散路径和门的利用效率低于休息期间。

4)将疏散场景B1、B2、C1和C3进行对比，在疏散人数相同的情况下，由于疏散发生时间段不同，人员预运动时间区别较大。对比疏散场景B1和C1，2个疏散场景除人员预运动时间外其余条件基本相同，由于人员清醒时预运动时间较少，所以能较快进行疏散，因此疏散场景B1的疏散时间短小于C1，疏散效率明显大于C1。同样，对比疏散人数相同的疏散场景B1、B2、C1和C3，场景B1和B2的疏散效率均大于场景C1和C3，说明人员清醒时的疏散效率大于睡眠时的疏散效率。

4 宿舍楼人员预期火灾风险评估

4.1 建筑火灾伤亡人数函数模型构建

假定火灾发生前，建筑内总人数为n，对于火灾发生后的任意时间t，未疏散的人数如式(2)所示：

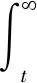
(2)

式中：h(t)为火灾发生后时间为t时未进行疏散的人数，人；t为火灾发生时间，s；n为建筑内的总人数，人；fE(t)为建筑内个体疏散时间的概率密度函数。

ASET的大小取决于火灾发展的速度和烟气的流动速度，火灾发生后仍然留在建筑物中的人数可能受火灾发展状况的影响，然而ASET在某时间t的发生概率几乎不依赖于在同一时间仍然留在建筑物中的人数。因此，假设上述因素对于简单计算是相互独立的，对于任意时间t，火灾伤亡人数如式(3)所示：

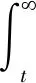
(3)

式中：c(t)为火灾发生后时间为t时，火灾中的人员伤亡数量，人；fA(t)为ASET的概率密度函数。

所以当火灾发生后，火灾造成的伤亡总人数如式(4)所示：

(4)

式中：C为火灾发生后火灾中人员伤亡总数，人。

由式(4)可知，通过对可用疏散时间概率密度函数fA(t)和火灾未疏散人数与时间函数h(t)的乘积进行积分，即可获得不同火灾场景下的伤亡人数。

4.2 宿舍楼人员预期火灾风险评估

将人员疏散模拟结果和火灾模拟结果相联系，将模拟结果的参数代入式(4)，可得宿舍楼火灾不同场景下的伤亡人数，见表5。

对于不同火灾场景的伤亡人数，火灾场景4的伤亡人数相对最多，男女生伤亡人数分别为305，310人；其次为火灾场景2，男女生伤亡人数分别为220，224人；再者为火灾场景3，男女生伤亡人数分别为23，27人；火灾场景1的伤亡人数相对最少，男女生伤亡人数小于0.01，所以未纳入统计。从火灾伤亡人数来看，火灾场景2和4的伤亡人数高达200人以上，因此，当前宿舍楼无法满足火灾安全的需求。

5 结论

1)火灾模拟得出，发生火灾后，影响ASET的主要因素是火灾烟气能见度，次要影响因素是烟气层温度，CO浓度对ASET的影响相对最小。对于平面呈L型的宿舍楼，当宿舍楼中部发生火灾后，烟气蔓延速度要快于宿舍楼两侧，可用疏散时间更短。

2)使用Pathfinder模拟软件对宿舍楼火灾疏散进行模拟，得到宿舍楼火灾发生后未疏散人数与时间的函数，将该函数与ASET的概率密度函数相乘，并对时间进行积分，可获得不同火灾场景下的伤亡人数，从而对宿舍人员火灾风险进行定量化评估，该方法可用于高校宿舍火灾的风险评估。

3)对于不同火灾场景的伤亡人数，火灾场景2和4的伤亡人数高达200人以上，主要是由于机械排烟系统故障导致。经上述方法评估，该宿舍楼无法满足火灾安全性需求，消防安全管理水平有待提高。