海上风机桩筒复合基础的水平承载性能分析

周恩全， 许 想， 陆建飞

(江苏大学 土木工程与力学学院， 江苏 镇江 212013)

风能作为一种绿色可再生能源，已成为全球能源开发的焦点.我国的海域辽阔，海岸线全长约有1.8万公里，拥有丰富的风能资源，发展海上风电，充分利用近海风能资源，将有效减少西电东送的运输成本，缓解我国沿海人口分布稠密区域的电力紧张状态.发展海上风电与陆地风电不同，海上风机所处海洋环境恶劣，承受的荷载种类较多，且十分复杂，基础结构的安全稳定是保证海上风电稳定运行的关键要素之一.海上风电基础依据外形、材料属性和施工方式的不同，可以划分为单桩基础、导管架基础、重力式基础、筒型基础以及浮式基础[1].

筒型基础的建设由于工程量少、投资少、施工简易以及可重复使用的特点，成为近年来应用前景较好的一种基础形式.闫澍旺等[2]对风电筒型基础的承载特性进行了三维有限元数值分析，得到单向加载下地基土体的破坏区域及破坏模式.M. ACHMUS等[3]采用数值模拟方法，研究了筒型基础在单调荷载作用下的承载性能，建立了荷载-弯矩相互作用曲线的量纲一化方程.王爱霞等[4]开展模型试验，对筒型基础在荷载作用下的变形和受力特性进行分析，结果表明在水平荷载作用下，筒型基础绕基础内某一深度的点转动，基础受压侧压入土体内部，受拉侧与土体逐渐脱离.FAN Q. L.等[5]通过三维有限元数值分析，研究了饱和黏土中筒型基础在循环荷载作用下的动力响应，结果表明在循环载荷下，弯矩-转角曲线近似为线弹性，且受到了土体侧壁界面条件的影响.LIU M. M.等[6]通过试验和有限元方法研究了筒型基础的承载力，发现转动是筒型基础的主要破坏形式，且转动中心位置随筒型基础高径比的变化而变化.SUN L. Q.等[7]通过有限元方法分析了黏土中筒型基础的抗拉能力，提出一种可预测不同长宽比和不同排水条件下筒型基础的抗拉能力分析方法.H.HIRAI[8]通过数值模拟法，对圆柱型基础和矩型基础在竖向、水平方向以及弯矩荷载作用下的变形和破坏进行了研究，从荷载与位移的关系、弯矩与转角的关系角度探讨了筒型基础周边砂土破坏前的单调特性.

筒型基础的研究和应用日趋成熟，然而随着海上风电技术不断发展、发电效率的进一步提升，海上风电机组向深远海和大型化发展已成为必然趋势，风电发展需要承载力越来越大的基础.为了提高传统筒型基础的承载力，笔者提出一种钢管桩与筒型基础组合形成的桩筒复合基础，理论推导适用于桩筒复合基础水平承载力的计算公式，并建立有限元分析模型，考虑用钢量不变的条件下，研究不同桩数条件下桩筒复合基础的水平承载力、应力响应及地基土破坏特性.

1 水平极限承载力理论分析

考虑到基础与地基土之间的相互作用效应是影响风电基础水平承载力的核心因素之一，因此在传统筒型基础的内部增加钢管桩，形成桩筒复合基础，增加基础的整体刚度，扩大基础与地基土的接触面积，提升基础与地基土的协同度.作用在桩筒复合基础上的水平荷载由外筒、钢管桩及地基土共同承担.笔者结合筒型基础及桩基础水平承载力的相关研究成果[9-11]，依据筒型基础受荷变位机制，在水平荷载p的作用下，假定桩筒复合基础的转动中心为中轴线上筒底中心O1，此时基础主要受到筒壁被动区侧向土体抗力pBp、筒壁主动区侧向土体抗力pBa、桩壁被动区侧向土体抗力pPp、桩壁主动区侧向土体抗力pPa、基底竖向抗力pz、基底总剪切力T以及筒土间摩擦力F1和F2的共同作用.其分布形式如图1所示.

图1 水平荷载下桩筒复合基础受力示意图

1) 假定筒壁被动区及桩壁被动区侧向土压力强度σp均为二次抛物线形分布，则有

σp=ωkz(L-z)cos2θ，

(1)

式中：ω为基础在水平荷载作用下的转动角度，rad；L为基础埋深，m;k为土的水平抗力系数，MPa·m-2；θ为筒壁或桩壁被动区上任意一点与原点O的连线在xOy平面上的投影与x轴正向夹角，(°)；z为筒壁或桩壁被动区某点深度，m.

筒壁被动区侧向土体抗力pBp及桩壁被动区侧向土体抗力pPp分别为

(2)

(3)

式中：R为筒体半径，m；Ri为桩半径，m；i为筒内桩的数量，个.

2) 假定筒壁主动区及桩壁主动区侧向土压力强度σa均呈三角形分布，则有

σa=Kaγz，

(4)

式中:Ka为朗肯主动土压力系数；γ为土体天然重度,kN·m-3.筒壁主动区侧向土体抗力pBa及桩壁被动区侧向土体抗力pPa分别为

(5)

(6)

3) 假定竖向基底压力强度σz服从Winkler假定，则有

σz=xωK0，

(7)

式中：x为竖向抗力作用点到基础中轴线水平距离，m；K0为深度h处竖向地基系数.基底竖向抗力为

(8)

4) 基底总剪切力T由筒底与土之间的摩擦力提供[12]，即

T=2πR2fkL(L-z0)，

(9)

式中：z0为转动中心深度，m；f为筒土间的摩擦系数.

5) 作用于筒壁外侧的单位摩擦力Fz与筒壁径向水平土压力成正比：

Fz=fωkz(L-z)cosθ.

(10)

则筒壁与土之间摩擦力F1和F2为

(11)

根据静力平衡和力矩平衡条件，可推导出桩筒复合基础水平承载力公式为

(12)

式中：D为外筒直径，m；Di为桩的直径，m.

从式(12)可以看出，相比单独筒型基础，桩筒复合基础的水平承载力显著提高，该水平承载力与外筒直径、桩数、桩径以及地基土条件有关.

2 有限元计算模型

利用ABAQUS有限元软件，对桩筒复合基础的水平承载特性进行分析.以江苏灌云5 MW风机为研究对象，在保持用钢量不变的条件下，研究单筒基础(B0P)、单筒加1桩基础(B1P)、单筒加3桩基础(B3P)及单筒加4桩基础(B4P)等4种基础形式的水平承载力特性.图2为4种基础形式有限元模型.4种基础形式相关参数见表1.

图2 4种基础有限元模型

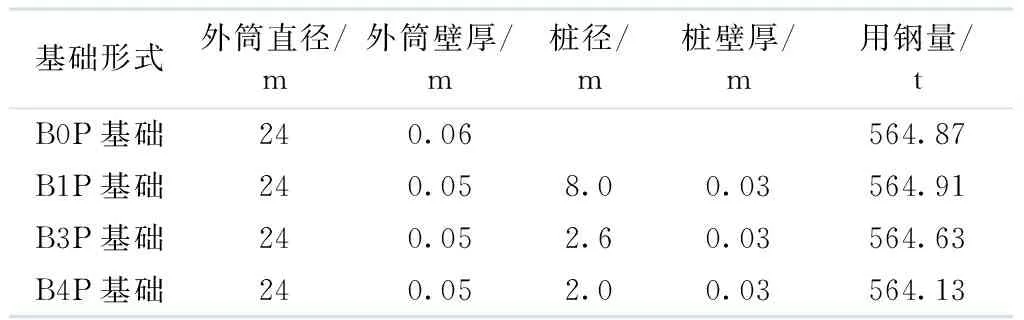
表1 4种基础形式相关参数

基础整体为钢结构，钢的密度为7 850 kg·m-3，杨氏模量为2.1×105MPa，泊松比为0.30，屈服强度为345 MPa.地基土采用Mohr-Coulomb本构模型，土的密度为1 930 kg·m-3，弹性模量为12.1 MPa，泊松比为0.33，摩擦角为25.7°.

基础和土体均采用六面体八节点线性减缩积分实体单元(C3D8R)，建立直径为80 m、高度为60 m的圆柱形土体模型，可有效消除土体有限边界对计算结果的影响[13]，提高计算的准确度.土体底部边界采取固定约束，四周采取径向约束.基础与土的接触面均采用“surface-to-surface”接触，切向行为采用“Penalty”接触，摩擦系数设置为0.25，法向行为采用“Hard”接触，允许接触后分离.

图3为桩筒复合基础模型加载点分布及加载方向示意图.采用位移加载法对桩筒复合基础模型施加水平位移l，分析其承载性能.加载点设计在桩筒复合基础上部过渡段的端部，距离筒顶8 m，加载点与过渡段端部采用耦合连接，使荷载均匀分布到过渡段端部平面上，以符合实际情况.

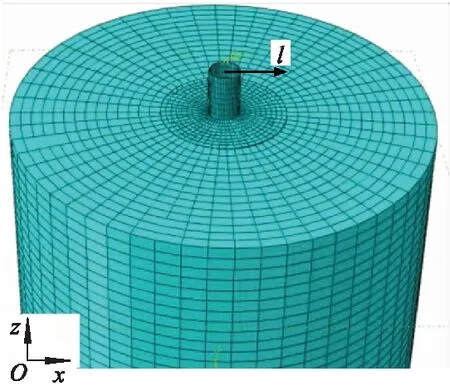
图3 桩筒复合基础模型加载点分布及加载方向示意图

3 基础承载力分析结果

3.1 基础极限承载力分析

图4为水平位移加载条件下加载点的荷载-位移曲线.由图4可知：B0P基础曲线表现出典型的准弹性—弹塑性—破坏的三阶段特性，而B1P、B3P和B4P基础的曲线表现出准弹性—弹塑性的二阶段特性，并未达到明显的破坏阶段；在加载前期，B0P基础的水平承载力明显最优，因为该阶段的水平荷载主要由外筒负担，B0P基础的筒壁最厚，刚度最大，承载力显然更优；随着持续加载，B0P基础逐渐失效，无法继续承担荷载，而桩筒复合基础中的桩基开始工作，显著提升了桩筒复合基础的水平承载力.

图4 水平位移加载条件下加载点的荷载-位移曲线

根据图4，取B0P基础荷载-位移曲线接近水平变化时所对应的荷载为该基础的极限承载力，取B1P、B3P和B4P基础达到最大位移4 m时所对应的荷载为相应基础的极限承载力，则B0P、B1P、B3P和B4P基础的水平极限承载力分别为36.16、52.17、49.09和48.72 MN.可见，在基础用钢量相等的条件下，桩筒复合基础的水平极限承载力明显高于单筒基础.但桩筒复合基础的极限承载力与筒内桩数无明显正相关关系，具体表现如下：B1P基础的水平极限承载力得到了最大程度的发挥，相比于B0P基础提高了约44.27%；B3P基础比B0P基础提高了约35.76%；B4P基础比B0P基础提高了约34.73%.也即在同样用钢量条件下，桩的数量越多，基础的承载力反而越低.

根据理论分析公式(12)计算得到B0P、B1P、B3P和B4P基础的水平极限承载力分别为40.64、54.20、51.80和50.21 MN，与根据图4数值模拟的水平极限承载力数值非常接近.

桩筒复合基础由外筒和桩组合而成，相比筒型基础而言，一方面桩筒复合基础与土体拥有更多的接触面积，有更高的协同度，在水平荷载作用下，地基土对桩筒复合基础会产生更大的土体抗力，使其承载性能得到显著提高.另一方面，在保持用钢量一致的情况下，B1P、B3P和B4P基础中桩与地基土的接触面积一致，基础的等效刚度同样一致，但B1P基础相比B3P、B4P整体性更好，承载力相对更高.

3.2 地基土等效塑性应变分析

图5为位移为4 m时，4种基础地基土的等效塑性应变分布云图.从图5中可以发现：基础形式不同，地基土的整体破坏模式相同，地基土的等效塑性应变区主要分布在被动区一侧；伴随施加位移的不断增大，基础挤压被动区土体，土压力逐渐增大，导致被动区地基土发生楔形等效塑性破坏；在主动区一侧，基础与地基土缓慢分离，不发生明显的塑性破坏.由此可见，在位移加载条件下，4种基础形式的地基土都产生楔形破坏，这是风机基础周围土体受外力作用的主要破坏模式.

图5 4种基础地基土的等效塑性应变分布云图

由图5还可知，当位移达到4 m时，等效塑性应变由大至小依次为B1P、B3P、B4P和B0P，其中B1P和B3P基础筒内地基土均有明显塑性应变，B4P和B0P基础无明显塑性应变.这与图4所展示出来的极限承载力呈正相关关系，即极限承载力越高，塑性应变越明显.原因是桩筒复合基础承载力提高是因为桩基的介入，强化了基础与地基土的协同作用，因此承载力越高，地基土分担的荷载比例越高，则地基土塑性应变越显著.

3.3 桩筒复合基础受力特性分析

图6为以B1P基础为例，沿深度方向的桩侧土压力变化曲线.由图6可知：基础的筒壁以及钢管桩桩壁被动区土压力数值呈先增大后减小的趋势，分布形式近似为二次抛物线(见图6a)，与图1所假设的σp分布形态一致；筒型基础的筒壁以及钢管桩桩壁主动区土压力沿深度不断增加，分布形式近似线性增长(见图6b)，与图1所假设的σa分布形态一致.

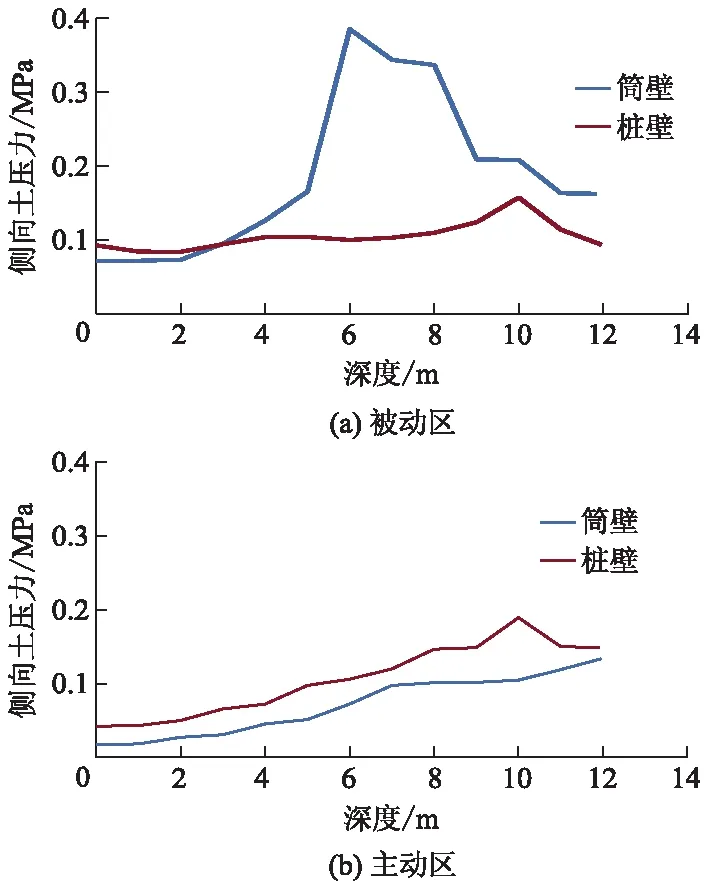
图6 B1P基础侧向土压力与深度关系曲线

图7为桩筒复合基础沿竖向的应力分布云图.由图7可知：不同结构的最危险位置均集中于基础的顶盖位置及上部结构与顶盖的连结段，表明主要由基础顶盖区域承担荷载；单就筒壁而言，被动侧的应力明显高于主动侧应力，显然这是因为被动侧地基土分担了更多的荷载，被动侧筒与土之间有更明显的相互作用，而主动侧筒与土之间相互作用不明显，甚至出现脱开；筒壁顶部及筒壁底部的应力分布大于筒壁中部.

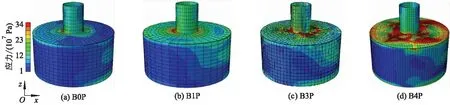
图7 4种基础沿竖向的应力分布云图

图8为位移达到4 m时，B0P、B1P、B3P和B4P等4种基础被动区筒壁应力沿深度方向的变化曲线.由图8可知：B0P、B1P、B3P和B4P等4种基础的筒壁应力沿深度向下呈现出减小—增大—减小—增大的发展模式；B0P基础的筒壁应力最小，这是因为在此状态下B0P基础已经失效，无法继续承担荷载；B3P与B4P基础的应力发展基本一致；总体上B1P基础的应力要小于B3P基础和B4P基础.

图8 筒壁不同深度处的压力与深度关系曲线

图9为B0P、B1P、B3P和B4P基础顶盖处的应力分布云图.由图9可知：B1P基础顶盖的峰值应力最小；B0P基础的高应力分布区域最窄，这是因为此状态下，B0P基础已经失效，无法继续承担荷载；B4P基础的高应力分布区域最广，其次是B3P、B1P基础，显然是因为B4P基础被动侧地基土分担的荷载最小，而B1P基础被动侧地基土分担的荷载最大；高应力分布区域主要集中在桩筒连结区域以及上部结构与顶盖的连结段，也就是说桩筒的连结以及上部结构与顶盖连结形成了应力集中区.

图9 4种基础顶盖处应力分布云图

图10为B1P、B3P和B4P基础的桩身应力分布云图.由图10可知：B1P、B3P和B4P基础的桩身可以有效将上部荷载传递给地基，所有桩身的高应力区均集中在桩顶部，且沿桩身向下逐渐减小；B1P基础桩身的应力峰值最小，其次是B4P和B3P基础.

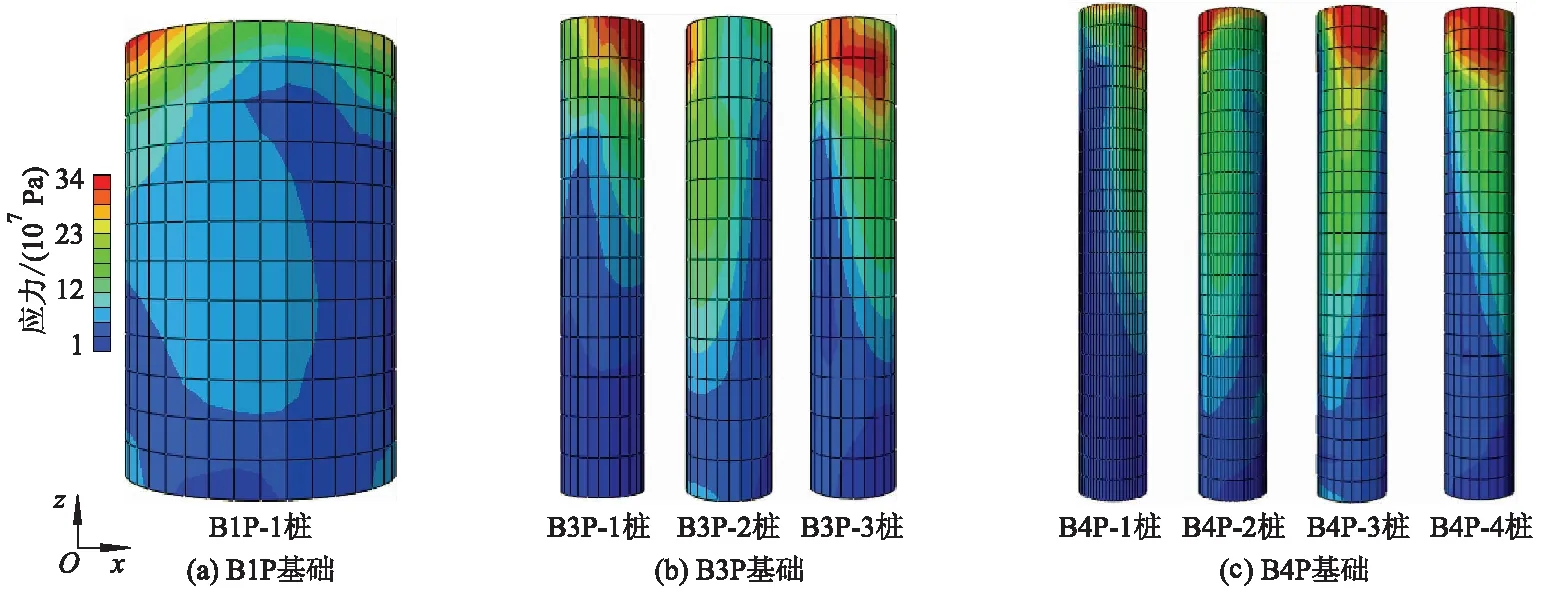
图10 桩筒复合基础桩身应力分布云图

4 结 论

1) 针对该钢管桩与筒型基础组合而成的桩筒复合基础形式，基于基础与地基土相互作用的极限平衡状态，提出了考虑不同桩数的桩筒复合基础水平承载力理论计算公式.

2) 在保持用钢量不变的前提下，桩筒复合基础相比筒型基础具有更高的承载能力，但桩筒复合基础的极限承载力与筒内桩数无明显正相关关系，提高承载能力需要综合考虑筒内钢管桩的直径、数量、布置方式等因素的影响.

3) 基础形式不同，地基土的整体破坏模式相同，地基土的塑性应变区主要分布在被动区一侧，表现出楔形破坏；地基土塑性应变越明显，表明其承担的荷载比例越高，基础的承载力越高.

4) 桩筒复合基础的高应力区域集中在基础顶盖，且顶盖高应力区分布越广，基础承载力越低.