海上风机导管架基础灌浆连接偏心受压承载性能研究

游先辉

（福建永福电力设计股份有限公司 福建福州 350001）

0 引言

为实现“碳中和”的目标，我国正大力优化能源结构，发展可再生能源，不断削减传统能源的比重。风能是优质可再生能源，是全球迎合“碳达峰、碳中和”的重要手段。相比陆上，海上风能不仅稳定、发电效率高、储量丰富，而且无噪音干扰、环境污染等问题，因而适合大规模开发和建设，近年来在我国沿海各省份迅速发展。随着海上风电建设技术的逐步成熟，目前已基本建立起完整的海上风电制造及施工体系。现有海上风电导管架基础结构大多数采用先桩法：先通过定位架将多根桩在一定精度条件下打入海床，再通过大型浮吊将导管架与桩整体对位，将多根支撑腿同时插入多根桩内，再灌注连接段灌浆料。由于海上风电建造环境比较苛刻，受风浪的影响，结构在对位时无法做到绝对静止，灌浆连接段的对位偏差必然形成，造成灌浆体厚度一侧薄一侧厚，连接结构受偏心力，进而影响灌浆连接段的性能。

目前少数学者开展了灌浆连接段尺寸偏心的研究，但多数针对的是弯矩作用下的结构性能。Lamport 等［1］对尺寸偏心的灌浆连接进行轴向静力试验，试验结果显示尺寸偏心对灌浆连接极限承载力存在一定影响，试验构件承载力相差最大可达15%左右。Lamport 的研究虽然具有一定的意义，但其试验采用的灌浆材料强度远小于目前海上风电导管架结构采用的灌浆材料强度。李筑轩等［2］对2 个尺寸偏心影响的灌浆连接进行了弯曲静力试验，试验发现灌浆连接破坏形式主要为钢管大幅度屈曲以及灌浆料端部局部脱离；试验发现尺寸偏心对于灌浆连接受弯承载力及其刚度影响较小。Chen 等［3］人对尺寸偏心灌浆连接进行弯曲静力试验，试验发现尺寸偏心的加入使得灌浆连接径向裂纹出现严重的扩展，尺寸偏心对灌浆连接受弯承载力、延性及刚度影响较小，但灌浆料较薄侧应变相较于无尺寸偏心灌浆连接应变更大，且灌浆较薄侧出现更为明显密集的裂纹。

由于国内外灌浆连接段偏心受压性能研究较少，现有规范的计算方法均未明确评估偏心受压对灌浆连接段承载性能的影响。因此本文结合试验和数值分析，针对灌浆连接段偏心受压性能进行了深入的研究和分析。

1 试验研究

1.1 试件设计

本试验采用实际工程中6.7 MW 海上风机导管架基础灌浆连接作为设计原型，以1∶4 的比例进行等比例缩小，在满足DNVGL 规范构造要求前提下，设计了无尺寸偏心的灌浆连接试件S1 及有尺寸偏心的灌浆连接试件S2。

灌浆连接试件是由钢套管、钢管桩、剪力键以及钢管之间灌浆料组成。试件外形及尺寸如图1 所示，计得偏心率Re=0.005（Re=e/Ds）。具体尺寸参数如表1 所示。

表1 试件尺寸表

图1 灌浆连接段参数示意图

1.2 试件制作

灌浆连接中钢构件采用Q345 高强钢作为钢管母材，剪力键采用φ6 光圆钢筋进行制作。灌浆材料使用国产高强灌浆材料UHPG120。灌浆连接试件制作包括：钢结构加工制作、灌浆前准备工作、灌浆工作以及灌浆后养护工作。

钢构件加工制作于加工厂内完成。钢构件加工完成后，将试件运至预制场进行灌浆准备工作及后续灌浆工作。

灌浆前准备工作包括：①采用EPC 高密度泡沫板填充钢套管底部，起到替代灌浆封隔器进行灌浆封堵作用；②钢管桩及钢套管对中后焊接支撑钢管起到支撑作用，并可以防止灌浆产生钢管桩及钢套管相对偏移问题。灌浆连接封浆前准备工作见图2 所示。

图2 试验准备工作

灌浆连接灌浆前准备工作完成后，进行灌浆工作。灌浆材料水料比按照灌浆材料使用说明多次试配，并采用卧式混凝土搅拌机进行搅拌，搅拌时间大于5 min，搅拌完成后对灌浆流动性进行检测，测得初始流动性满足控制于290 mm 左右且无泌水现象时进行灌浆。

1.3 材性测试

试件使用的钢管根据《金属材料 拉伸实验：第1 部分：室温试验方法》（GB/T228.1—2010）［4］进行钢片材拉伸实验。实测平均屈服强度398 MPa，平均抗拉强度571 MPa，平均弹性模量210×104 MPa，泊松比为0.304。

试件灌浆材料根据 《Support structures for wind turbines》（DNVGL-ST-0126）［5］要求，每根试件浇筑所用灌浆料制作3个75 mm×75 mm 立方体试块进行抗压强度测试，灌浆料的材性试验结果如表2 所示。

表2 灌浆材料性能

1.4 试验装置及加载方式

本试验采用10 000 kN 液压伺服长柱试验机，对试件进行试验加载，数据采集采用东华DH3816 静态应变测试采集系统和试液压伺服长柱试验机控制反馈系统。

试验加载采用预加载及正式加载方式。预加载用以消除灌浆连接虚位移、来检查各仪器设备运行是否正常。预加载荷载取为预计极限承载力的30%，采用力控制分级加载方式，每完成一级加载，持载2 min，用以检测设备及试件是否正常。

正式加载采用力-位移共同控制的加载方式。在达到预计计算极限承载力70%之前，采用力控制加载，并采用分级加载制度进行加载。每级加载完成后持载2 min，确保各采集数据无明显问题后继续加载。当加载至预计极限承载力70%后改用位移控制方式进行加载，加载速率采用0.2 mm/min，加载直至试件破坏。

1.5 测试方案

试验采用位移计测量试件整体位移及钢套管与钢管桩之间相对位移，使用应变片测量钢套管外壁及钢管桩内壁测点应变变化情况。

试验布置3 个50 mm 行程的位移计。应变片均匀布置于灌浆连接0°、90°、180°、270°侧，分别布置于每侧剪力键附近以及加劲肋内侧无灌浆料处钢管之上，测点示意见图3。

图3 应变计和位移计布置士意图

1.6 试验现象

试件S1 加载初期，试件处于弹性阶段，无明显试验现象。随荷载持续稳定增加，当荷载增加至2 071 kN 时，首次出现响声，响声较小，此时灌浆与钢管间应出现粘结滑移；当荷载增至3 270 kN 时，试件S1 出现明显的清脆响声，使荷载继续增加，响声出现更加频繁，结合试验结果，此时剪力键附近灌浆应出现较大程度压碎，剪力键附近灌浆裂纹开始发展；荷载加至4 691 kN 时，试件出现连续巨大响声，此时响声较为沉闷，结合试验结果，试件灌浆裂纹出现明显发展，甚至出现贯穿灌浆的裂缝，在几次巨响出现后，试件破坏，试验机停止加载。

试件S2 试验现象与试件S1 试验现象基本相同。加载初期，试件处于弹性阶段，期间无明显试验现象。当荷载增加至1 738 kN 时，出现较小的响声，此时灌浆与钢管间应出现粘结滑移，灌浆与剪力键开始挤压；当荷载继续增至3 022 kN 时，试件出现明显清脆响声，此时剪力键附近灌浆应出现压碎现象；荷载继续增加至4 038 kN 时，试件出现巨大沉闷响声，此时剪力键附近灌浆裂纹出现较大程度的发展，灌浆可能出现贯穿开裂；试验机继续加载，在出现几次巨大响声后，试件发生破坏。

1.7 试验结果分析

试验获得试件荷载位移曲线如图4 所示。从图4 可以发现：无尺寸偏心的试件S1 极限承载力为4 948 kN，试件位移为2.1 mm。试件S1 荷载位移曲线前期呈线性稳定增加，当荷载增加至3 270 kN 时，此时荷载位移曲线出现小幅下降；荷载继续增加至4 691 kN 时，承载力突然降低，随后承载力继续上升，但刚度明显下降；荷载增加至4 948 kN，试件达到极限承载力，随后试件承载力急速下降，试验机停止加载。有尺寸偏心的试件S2 与试件S1 的荷载位移曲线前期变化基本一致，试件S2 荷载位移曲线前期呈线性增加，当荷载加至3 022 kN时，试件承载力出现较明显的降低情况，此时剪力键附近灌浆应被挤压破碎；荷载继续增加至4 038 kN 时，试件S2 极达到极限承载力，随后结构经过几次内力重分布，位移不断增加，但承载力不再上升。

图4 荷载位移曲线

对比荷载位移曲线可以发现，试验中尺寸偏心试件S1 与无偏心试件S2 前期刚度基本一致，因此尺寸偏心对灌浆连接前期刚度影响较小。从试验结果可以发现尺寸偏心的降低了灌浆连接承载力，当偏心距e=30 mm（Re=0.05）时，尺寸偏心试件极限承载力为无偏心试件极限承载力的81.6%。

图5 给出了试件S1 与S2 试验所得荷载—应变曲线，S1应变取不同角度平均值进行分析，S2 应变从不同角度进行分析。当试件S1 荷载增加至3 500 kN 时，试件S2 荷载增加至3 000 kN 时，剪力键附近纵向应变，出现反向增长的趋势，纵向应变由受压状态变为受拉状态，越靠近加载端，纵向应变反向增加越明显。出现这种情况主要原因为剪力键附近灌浆压碎后体积膨胀导致，灌浆体积膨胀使钢管纵向应变由受压状态变为受拉状态。

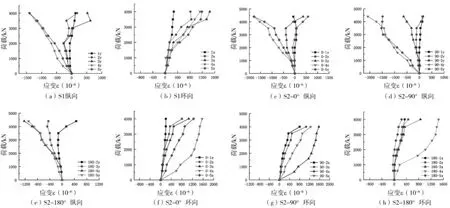
图5 荷载应变曲线

试件S1 与S2 环向应变始终处于受拉状态，应变呈线性增长趋势，试件S1 荷载增加至3 500 kN 左右时，试件S1 荷载加至3 000 kN 时，试件环向应变增加，主要原因为灌浆压碎产生体的灌浆体积膨胀使得环向应变增大。试件的尺寸偏心使得灌浆料提前出现破坏征兆。

对比发现加劲肋内侧环向应变及纵向应变均大于剪力键附近应变，灌浆约束了钢管应变的发展；越靠近加载端剪力键附近钢管应变越大。

1.8 灌浆连接破坏模式

图6 试件破坏形式示意

灌浆内部破坏主要为相邻剪力键之间灌浆斜向贯穿开裂。贯穿开裂主要出现在钢套管底部剪力键与钢管桩中部剪力键之间，钢套管中部剪力键与钢管桩顶部剪力键之间；不同于试件S1 破坏模式，试件S2 较薄侧灌浆裂缝开裂角度较大，裂缝沿剪力键横向发展，随灌浆厚度的增加，开裂角度逐渐变小，裂缝沿剪力键横向发展逐渐变为沿剪力键之间斜向发展，且较薄处破坏更严重。

2 有限元分析

2.1 模型建立

有限元模型中包含钢材及灌浆2 种材料。钢材采用随动强化理论，灌浆材料使用混凝土损伤塑性模型（CDP）［6-7］，混凝土损伤定义则按照张劲等［8］进行参考设置。模型接触包括钢套管与灌浆料之间接触、钢管桩与灌浆料之间接触。接触设置由法线方向和切线方向的接触组成，法线方向采用硬接触，切线方向采用库伦摩擦［9］。网格采用实体单元进行建模分析。模型边界条件设置为钢管桩顶部进行固端约束约束。网格划分对计算结果精度有较大影响，研究发现钢管壁厚应设置不少于3层网格，剪力键附近网格进行加密处理［10-11］。

2.2 模型验证

为验证有限元模型正确性与合理性，通过有限元软件ABAQUS 对试件S1、S2 进行建模分析，结果如图7（a）（b）所示，可以发现试验极限承载力有限元模拟极限承载力基本一致，荷载位移曲线吻合度较好。将S1 试件破坏模式与有限元模拟进行对比发现，试验与有限元结果破坏模式基本一致。因此可以判断有限元有较高的准确性。

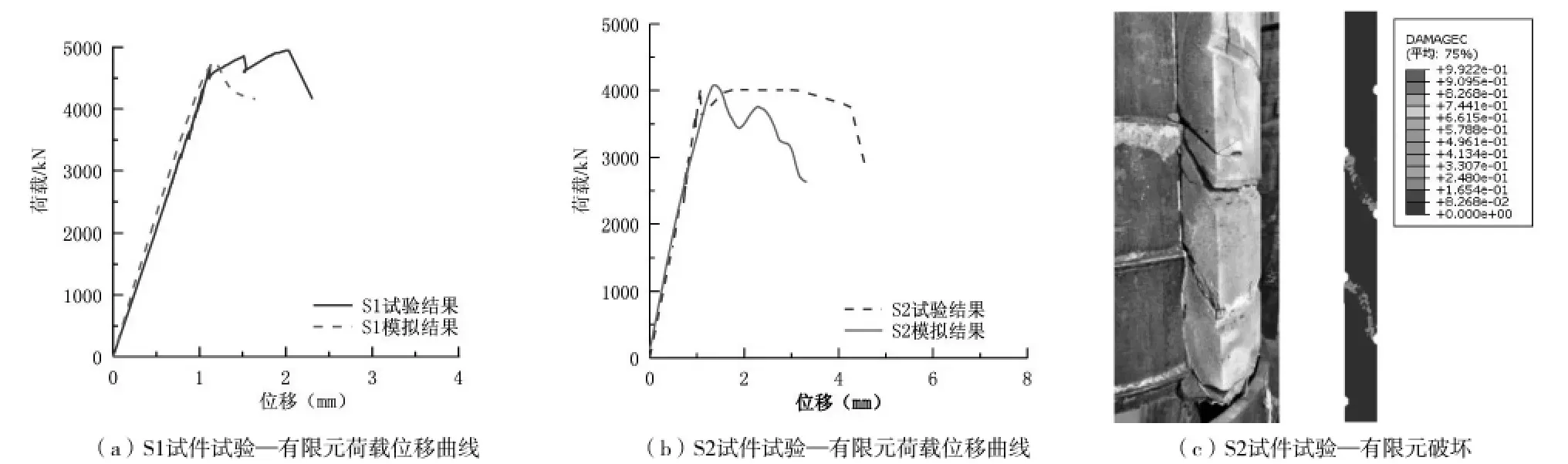
图7 有限元模型验证

2.3 参数分析

（1）不同偏心率计算分析。以灌浆连接试件尺寸为原型，建立不同偏心率灌浆连接模型进行分析对比。偏心率Re=0、0.008、0.017、0.025、0.033、0.042、0.050、0.058。

有限元计算获得不同偏心率的极限承载力，结果如图8所示。图中可以发现极限承载力随偏心距的增加而降低。当偏心距Re=0.058 时，尺寸偏心对灌浆连接极限承载力影响为22%。不同偏心率灌浆连接段前期刚度基本相同，随荷载继续增加，偏心率较大灌浆连接首先出现刚度退化，并率先达到极限承载力。

图8 不同偏心率模型荷载位移曲线

提取不同偏心距灌浆连接段剪力键附近灌浆料Tresca 应力进行对比分析，结果如图9 所示。图中可以发现，随着偏心距的增加，0°侧（灌浆料较薄侧）Tresca 应力逐渐变大，180°侧（灌浆料较厚侧）Tresca 应力变化较小。

图9 不同偏心距剪力键附近灌浆料最大Tresca 应力

（2）不同剪力键个数计算分析。建立有效剪力键个数n=2、4、6 的有限元模型，每种剪力键个数模型偏心率Re=0、0.016、0.032、0.050，对其极限承载力进行模拟分析，结果如图10（a），图中可以发现随有效剪力键个数增加，灌浆连接承载能力大幅提升；模拟发现尺寸偏心对不同剪力键个数灌浆连接极限承载力降低趋势及降低幅度基本相同。

（3）不同剪力键高距比计算分析。增加剪力键间距，建立不同剪力键高距比灌浆连接有限元模型，剪力键高距比h/s 分别为0.02、0.04、0.06、0.08，每种剪力键高距比模型建立偏心率Re=0、0.016、0.032、0.050 的尺寸偏心模型。对其极限承载力进行模拟分析，结果如图10（b），图中可以发现增大剪力键间距，减小剪力键高距比，能够明显提高灌浆连接承载力；尺寸偏心对不同剪力键高距比灌浆连接极限承载力降低趋势及降低幅度基本相同。

（4）不同钢管壁厚计算分析。建立钢套管壁厚ts=8 mm、12 mm、16 mm、20 mm，钢管桩壁厚tp=8 mm、12 mm、16 mm、20 mm 的尺寸偏心灌浆连接模型，偏心率Re=0、0.016、0.032、0.050，结果如图10（c）（d）所示。图中可以发现，灌浆连接极限承载力随钢管壁厚增加变化幅度较小；尺寸偏心对不同剪力键高距比灌浆连接极限承载力降低趋势及降低幅度基本相同。

沙沟一旦发生大规模泥石流灾害，其威胁对象主要为沟口南川区金山镇金狮村四社集中居民点，威胁金狮村小学、昆达农业有限公司和居民住户共161户604人的生命及财产安全。为此，研究沙沟泥石流的形成因素、物理力学特征参数和可能发生的危险性，针对该泥石流的特征，提出工程治理措施对保障人民群众生命财产安全，意义重大。

（5）不同灌浆厚度计算分析。建立灌浆料厚度tg=44 mm、48 mm、52 mm、55 mm 尺寸偏心模型，分别改变钢套管外径及钢管桩外径来改变灌浆厚度，模拟结果如图10（e）（f）所示。图中可以发现增加灌浆厚度对灌浆连接极限承载力小幅提高承载力；尺寸偏心对不同剪力键高距比灌浆连接极限承载力降低趋势基本相同。

（6）不同灌浆长度计算分析。建立灌浆长度lg=650 mm、1 000 mm、1 500 mm、2 000 mm 的尺寸偏心模型，模拟如图10（f）所示，图中发现增加灌浆长度，对灌浆连接极承载力提高较小；尺寸偏心对不同剪力键高距比灌浆连接极限承载力降低趋势基本相同。

图10 偏心条件下不同参数灌浆连接模拟结果

通过上述分析可见，参数的变化几乎不影响偏心率变化对灌浆连接段承载力带来的影响。

2.4 尺寸偏心灌浆连接承载力计算方法

DNVGL 规范［5］中导管架基础灌浆连接承载力公式中未考虑尺寸偏心对灌浆连接承载力影响，本文根据有限元参数分析结果，提出偏心折减系数，以便更好的计算实际工程中尺寸偏心对灌浆连接承载力影响。

根据已完成的尺寸偏心条件下灌浆连接参数分析结果，提出偏心折减系数φe，记为尺寸偏心的灌浆连极限接承载力Fe与无偏心灌浆连接极限承载力Fu的比值，计算方式如式（1）。

针对已完成的尺寸偏心条件下不同参数灌浆连接的有限元模拟结果，发现不同参数灌浆连接在尺寸偏心条件下承载力变化趋势基本一致，因此建立偏心折减系数与偏心率之间的关系。对比尺寸偏心条件下不同参数灌浆连接偏心率与偏心折减系数可以发现，偏心率与偏心折减系数大致呈二次关系，因此偏心折减系数与偏心率拟合公式形式如式（2）所示，其中φe为偏心折减系数，x 为偏心率。

考虑到不同参数灌浆连接有限元结果为较为理想状态下的计算结果，实际工程中常因各种外界因素存在一定的误差。基于安全考虑，采取尺寸偏心对不同参数灌浆连接影响最大值进行数据拟合，拟合结果如图11 所示，选取不同参数中尺寸偏心对灌浆连接影响最大拟合曲线作为偏心折减系数与偏心率之间关系，结果式（3）所示，尺寸偏心灌浆连接设计承载力计算公式可由式（1）～（4）进行计算：

图11 不同参数拟合曲线

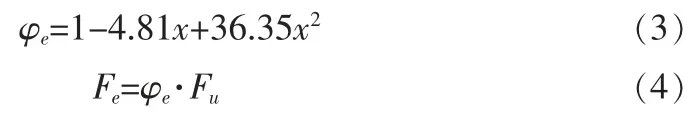
3 结论

通过对尺寸偏心及无偏心灌浆连接进行轴向静力试验，并结合有限元软件ABAQUS 进行相关参数分析，得到结论如下：

（1）尺寸偏心的灌浆连接段的承载能力有较明显的影响。灌浆连接破坏主要为灌浆的破坏，灌浆内部破坏表现为剪力键之间出现斜向贯穿开裂，灌浆较薄一侧更早发生剪切破坏。

（2）尺寸偏心对关键连接段轴向承载力存在一定影响。随偏心尺寸的增加，灌浆连接极限承载力随之降低。在满足规范构造要求条件下，偏心率Re=0.050 时，极限承载力降低幅度为14%；Re=0.058 时，灌浆连接不满足规范构造要求时，极限承载力降低幅度为22%。

（3）随偏心率的增加，灌浆连接段较薄侧灌浆裂纹发展角度逐渐变大，最大可达90°即裂纹沿剪力键横向发展；较厚侧灌浆仍沿剪力键斜向发展，裂纹发展角度随偏心率增加而减小。

（4）不同参数灌浆连接在相同偏心率条件下承载力降低幅度相差较小。根据参数分析结果，提出了考虑偏心影响的灌浆连接极限承载力计算方法，为尺寸偏心灌浆连接承载力计算提供理论基础。