不同滩形对卷波破碎引起的紊动能量与能损分析

刘文帅 ，郑建国* ，张翀岳，金智涛，许国辉

(1.中国海洋大学 海洋环境与生态教育部重点实验室，山东 青岛266100；2.中国海洋大学 山东省海洋环境地质工程重点实验室，山东 青岛266100；3.中国海洋大学 环境科学与工程学院，山东 青岛266100)

引 言

波浪由外海传至近岸，随水深变浅波高逐渐增大，无法维持较大的波陡时波浪就会发生破碎。波浪破碎引起强烈的水体紊动，能量损耗大。波浪破碎后会以新的波高继续向前传播，甚至可能发生多次破碎，直至能量消耗殆尽。波浪破碎涉及到剧烈的能量和动量交换，波浪能量的衰减及近岸水体运输都与这种交换作用有关。波浪的破碎易造成破碎区结构物的破坏，航道和港区的淤积等问题[1]，因此针对波浪破碎相关问题进行研究，能够更好地指导实际工程，也可以为岸线侵蚀的评估等实际问题提供一定参照。

目前许多国内外学者针对波浪破碎相关的能量问题作了大量理论模拟和试验探索，得到一些宝贵的实测资料和经验公式,为求解破后波、近岸区增减水等一系列问题提供了依据。邹志利[2]总结前人提出的破碎波能量损失波能方程，指出波能损耗率是计算关键，通过将计算波高与实测波高吻合，试图找到符合实际的波能损耗率。许多研究都在此基础上寻找更好的波能损耗率表达式，主要包括涌模型和水滚模型两种。

涌模型可描述波浪破碎过程及其能量的变化情况，破碎过程可分波浪变形剧烈的外区和滚动旋涡消耗能量为主的内区[3-4]，利用涌模型进行能量损失计算对波浪崩破及破碎内区有一定的模拟效果[5]，但涌模型无法解释破碎机理；而水滚模型是将波峰附近表层形成的混乱水体称为水滚，水滚的水平速度和波浪的相速度相同[6]，水滚和下面波浪之间的剪力摩擦是破碎能量损失的主要因素，单位面积的能量损失率与水滚的剖面面积有关[7]，不同的剖面面积可有不同的算法[4,8]，但众多参数之间的相互关系仍有争议。除上述两模型外，也有学者通过其他模型研究波浪破碎过程中的能量问题，主要包括Boussinesq方程[9-11]和缓坡方程[12-14]。

波浪破碎后，水体状态与紊流相似，因此可利用紊流模型来研究波浪破碎造成的能量损失问题。HORIKAWA等[15]根据各项同性紊流及孤立波理论，计算了破波能量损失问题，SAWARAGI等[16]指出波浪破碎形成的紊乱状态不是各向同性的，且Horikawa的计算中未能考虑到增水的影响，Mizuchi[17]进一步优化了破碎带内的能量方程。

尽管许多学者对于波浪能量等问题提出了很多见解，但大都未考虑过波浪浅化、破碎过程中滩面形态的影响。波浪破碎造成水体紊动和能量损失，并伴随着滩形变化，平直滩形最终发展形成沙纹滩形，不同滩形在同样波况下的紊动能量分布和破波能损可能是不同的。本文基于FLOW-3D软件，建立并验证了数值波浪水槽内的沙滩冲刷模型，通过固定欧拉网格求解Navier-Stokes方程，得到了平直滩形和沙纹滩形在多种工况卷破波作用下的紊动能量分布，并对比了多种工况下的波浪破碎能耗。

1 室内水槽试验

试验所用波浪水槽长宽高尺寸分别为14、0.5、0.6 m，水槽右端配有推板造波系统，靠近左端铺设试验用平直沙滩模型(试验用砂为取自青岛周边海滩筛分得到的中砂，D50=0.375 mm，各组分质量分数：0～0.25 mm占2.8%，0.25～0.5 mm占81.9%，0.5～1 mm占15.3%)，水槽两端均配备消浪设施以保证波浪稳定性。在沙滩坡脚设置1个波高仪，记录波高变化，具体试验设置见图1。试验主要内容为，观察特定波浪向左传播并在砂质岸滩上破碎过程中，破波点附近的波浪形态以及破碎对于岸滩造成的影响。在试验开始前和结束后，通过地形仪分别测得平直滩形和沙纹滩形(图2)。试验工况见表1，所有工况波浪破碎类型均为卷破波。

图1 试验设置示意图

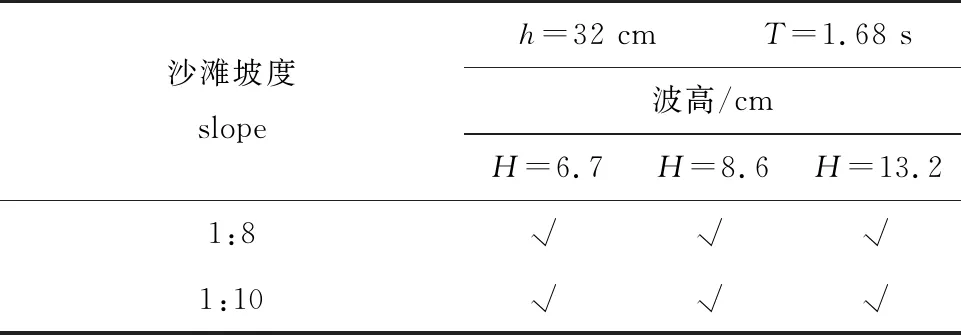
表1 工况设置表

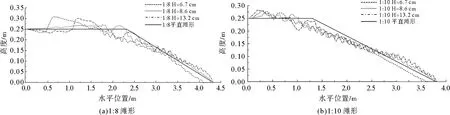
图2 各工况滩形

2 模型建立与验证

2.1 理论模型

FLOW-3D计算性能高，可以自定义多种物理场，广泛应用于不同领域，能够精准预测自由液面流动。FLOW-3D通过其独特的FAVORTM技术，将其各理论模型表达为体积和面积、孔隙度的函数，在模拟复杂几何区域时具有一定优势。本文所用计算模型主要包括连续方程、动量方程、流体自由面方程(VOF方法)及泥沙冲刷模型，紊流模型选取RNGk-ε紊流模型(求解速度快,精度高[18])。

2.1.1 连续性方程

(1)

2.1.2 动量方程

(2)

(3)

(4)

式中，p是压力；VF是流体所占体积分数，由FLOW-3D建模时确定；ρ为流体密度；u、v、w为在t时刻对应坐标上流速分量；Ax、Ay、Az为FLOW-3D在t时刻3个方向FAVORTM面积函数；Gx、Gy、Gz为加速度分量；fx、fy、fz为3个方向的粘性力。

2.1.3 流体自由面方程

流体自由面捕获采用流体体积法(VOF)，其方程如下：

(5)

(6)

式中,VF为扩散系数。

2.1.4 泥沙冲刷模型

FLOW-3D中的泥沙模型可用于计算泥沙的输运、冲刷和沉降，采用VOF方法模拟流体和泥沙的分界面[19]，泥沙以底沙(堆积在河床上的泥沙)和悬沙(流体中的泥沙)两种状态存在，悬沙浓度通过对流扩散方程控制。泥沙模型通过追踪底沙和悬沙的含沙浓度(Cp，Cs)，计算泥沙体积分数。总泥沙体积分数αs是网格中悬沙和底沙的总体积分数，表达式为：

(7)

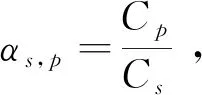
ρ=αfρf+(1-αf)ρs

(8)

式中，ρf为流体密度；ρs为泥沙密度；αf为网格中流体的体积分数。用当地密度替换Navier-Stokes方程中的流体密度，根据总含沙量在每个网格中计算出一对一的当地密度，粘性增量或者阻力增量引起的泥沙体积分数取决于αc0。

2.2 模型建立

采用FLOW-3D软件建立三维冲刷模型(宽度方向为单一网格)，FLOW-3D可以通过在固定欧拉网格中采用有限体积差分法求解三维瞬态Navier-Stokes方程。使用嵌套网格对滩形附近和自由水面波动范围内进行局部加密。数值波浪水槽一端(Xmin)为造波边界，为了消除回波反射的影响，在数值水槽的另一端(Xmax)设置多孔介质消波装置配合出流边界消除反射，具体设置及参数主要参考张婷[20]的相关设置，其他边界条件为Ymin,Ymax，Zmax：对称边界；Zmin：墙边界。计算时长为30 s，步长为0.05 s，网格总数为50万个，Z方向和X方向网格最小尺寸分别为0.002 75、0.004 m。

图3 网格划分图(局部)

2.3 模型验证

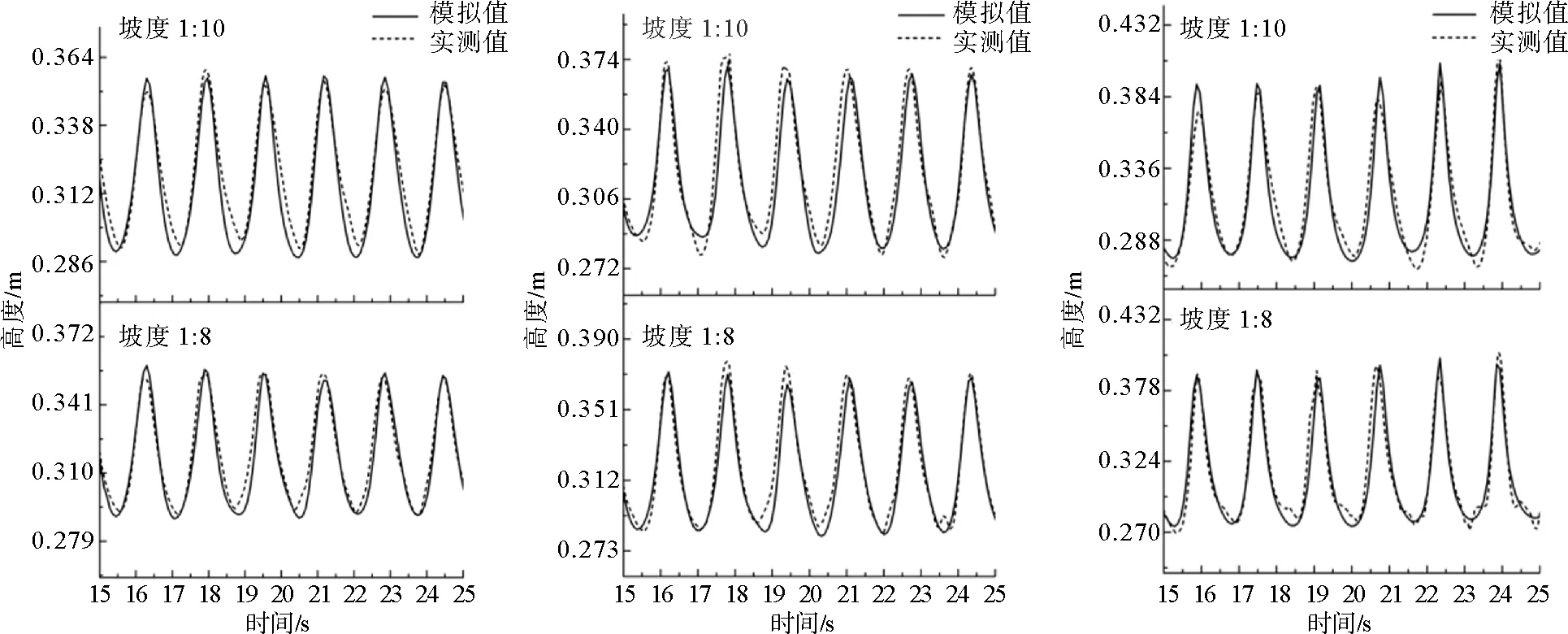
为验证数值波浪水槽的可靠性，在波形稳定阶段(15～25 s)从平直滩形坡脚自由水面时序曲线(图4)、波浪破碎形态(图5，平直滩形与沙纹滩形各选一例用于简要说明)两个方面进行验证。

(a) H=6.7 cm (b) H=8.6 cm (c) H=13.2 cm

图5 波浪破碎形态验证图(部分)

验证结果表明，稳定后自由水面时序曲线基本吻合(波峰、波谷最大误差分别不超过3.8%和4.2%)，波浪破碎形态模拟与实验对应关系良好,软件对于波浪在岸滩上的变形与运动具有良好的描述能力，能够较为准确地捕捉岸滩附近的水体，可用于进一步研究岸滩上的波浪破碎相关问题。

3 模拟结果

使用FLOW-3D提取了模拟结果中波形稳定时段(15～25 s)平直滩形与沙纹滩形波浪破碎前后水体自由水面时序曲线(图6)。

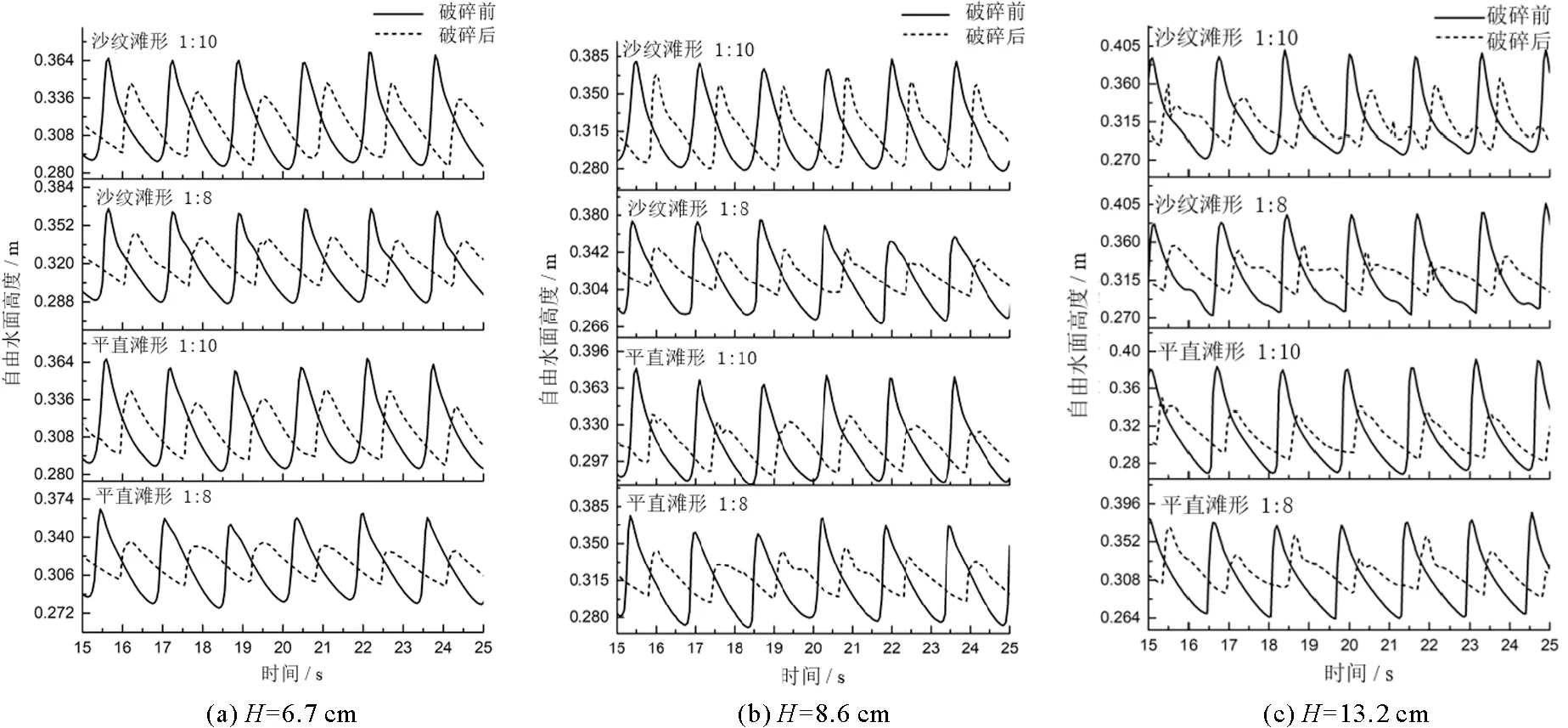
图6 破碎前后自由水面时序曲线图

计算结果表明，波浪破碎前，由于水深不断变浅，波浪表现出一定的非线性特征，随水深进一步变浅，波浪发生破碎，破碎后波浪非线性明显增强，且波高变化明显，波形与波高的变化表明了破碎造成波浪能量的变化，关于能量变化的具体分析详见下节。

4 分析与讨论

4.1 紊动能量

卷破波造成水体紊乱的基本模式为：波浪卷破前形成水舌，在水舌形成后至水舌溅落至水体前过程中，除底层水体因与表层沙滩相互作用造成较弱的水体紊动能量外，水舌表层也存在较弱的紊动能量(图7a,7b)。水舌形成后，由于重力、惯性的作用，向前方溅落，水舌头部溅落后迅速提升水体紊动程度(图7c,7d)，在波浪破碎的全过程中此时水体的紊动能量达到最大值，以溅落点为中心，紊动能量向附近扩散，周围水体也逐渐受到紊动影响。当波高较大时，波浪往往会发生多次破碎，其模式基本与前述大致相同，都在水舌头部溅落时达到紊动能量高值，并以溅落点为中心向周围水体扩散，直到水体只能形成微弱起伏，无法形成水舌，也无法再次破碎，因此后方水体基本不产生较大紊动能量。

图7 水舌形成、溅落图

本文统计了所有工况中的最大紊动能量值(图8)，发现最大紊动能量值与波高呈明显的正向相关性，这是因为波高增大时，破碎形成的水舌也随之变大，水舌溅落后在水体表面造成的紊动更强。而相同波况作用下，沙纹滩形水面最大紊动强度要小于平直滩形，在波高较大时，这一现象更加明显，这表明沙纹滩形会影响卷破波的破碎过程，尤其是水舌的形成和溅落过程，从而影响卷破波的紊动能量的大小与分布。所以，在分析讨论实际海滩对于卷破波紊动能量的大小和分布的影响时，不应当将实际滩形简化为表面平直具有一定坡度的斜坡，而是要充分考虑到凹凸不平的滩面形态对于水体流场的影响和作用。

图8 最大紊动能量统计图

4.2 破波能损

将破波前后水体的自由水面时序曲线通过快速傅里叶变换将数据从时域转换为频域，分离出各个子波，通过白志刚等[21]提出的波能计算方法分别求解各子波的波能后在一定时间内(取1个周期，即1.68 s)叠加，得到波浪破碎前后的波能，并计算得到波浪的能量破损率(图9)。

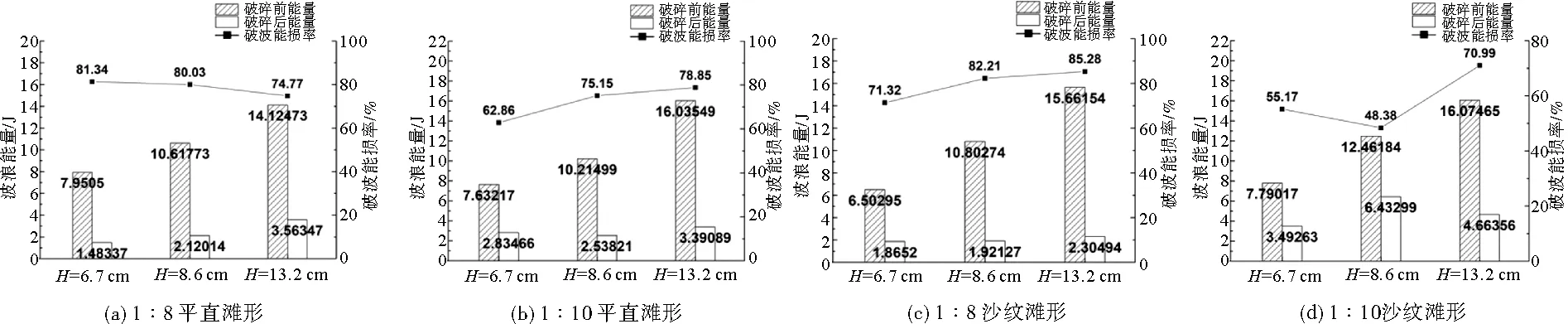
图9 各工况波浪能量破损率图

平直滩形，1:8坡度随着波高的增加,破波能损率逐渐降低；而1:10坡度的破波能损率呈相反趋势，随波高增加而逐渐提高。且在波高较小(H=6.7,8.6 cm)时，1:8坡度破波能损率要高于1:10坡度；而波高较大(H=13.2 cm)时，1:8坡度破波能损率低于1:10坡度。

沙纹滩形破波能损率变化较为复杂，伴随着波高的提高，破波能损率会出现陡增。其原因应与沙坝在破波区域中是否存在具有一定的关联性。1:8沙纹滩形在波高较小(H=6.7 cm)时，破波能损率较低，而波高增大至H=8.6,13.2 cm后，破波能损率分别提升12.29%和15.99%，而对于相同坡度波高较大的工况(H=8.6,13.2 cm)波高增大后破波能损率变化不大(3.7%);1:10滩形情况相似，在H=6.7,8.6 cm工况，破波能损率较低，分别为55.17%和48.38%，当波高增至H=13.2 cm时，破波能损率均有大幅提升，分别提升15.82%和22.61%。在所有破波能损率明显增大的工况中(1:8 H=8.6,13.2 cm；1:10 H=13.2 cm)，均在破波区域内出现明显沙坝，而破波能损率较小的工况(1:8 H=6.7 cm；1:10 H=6.7,8.6 cm) 则未出现明显沙坝。沙坝的存在，主要是由于波浪在沙滩上破碎后造成大量泥沙起动，在回落水流等的作用下沉积而最终形成。波浪传播至破波线附近时，由于水深变浅，波浪开始发生破碎，水舌初步形成，水舌向前传播过程中体积不断增大，当遭遇水下沙坝，水舌会越过沙坝向前运动，在水舌跨越沙坝过程中，由于水深急剧变浅，波浪难以维持水舌并进一步向前传播，在沙坝后方破碎，沙坝对于波浪破碎的作用与水下潜堤的效果相似。

此外，1:10坡度H=13.2 cm波况破波能损率除了受到沙坝的较大影响外，造成这一波况下破波能损率远高于同一坡度沙纹滩形其他两种波况的另外一个重要原因在于，水舌坠落后，由于沙滩地形的原因二次弹起的水舌分为两个部分，一部分水舌与其他工况相同，向前继续传播，而另一部分则是向反方向传播，造成了向前传播的水舌体积小于正常情况，较小体积的水舌在溅落时无法引起前方水体的较大幅度波动，因此前方水体波浪能量较小(图10)。

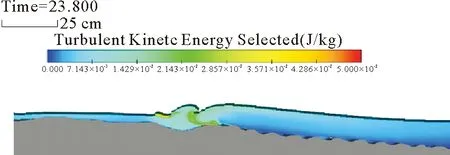
图10 波浪破碎模拟图 (1:10 H=13.2 cm)

5 结论

本文基于FLOW-3D软件，采用VOF方法描述水体的自由表面，建立并验证了三维岸滩波浪冲刷模型，探讨了卷破波在平直滩形和沙纹滩形上破碎的紊动能量分布与波浪破碎能耗，得到以下结论：

(1)波浪时序曲线、波浪破碎形态与实验结果基本吻合，表明本模型的合理性与可靠性。

(2)波浪卷破后，水体紊动能量在水面附近达到最大值，在深度方向上逐渐减小，沙纹滩形的紊动能量最大值小于同波况下的平直滩形，沙滩坡度与滩形会影响紊动能量在水体中的分布。在研究波浪破碎造成的紊动能量分布相关问题时，不能将滩形简化为表面平直具有一定坡度的斜面。

(3)平直滩形卷破波的破波能损与波高的关系受坡度影响，1:8平直滩形破波能损随波高增大而逐渐减小，1:10平直滩形破波能损随波高增大而逐渐增大；沙纹滩形卷破波的破波能损与滩形在破波区域内是否发育出现沙坝有较大关系，沙坝的出现提高了卷破波的能量耗损率。滩形的起伏通过阻碍水舌弹起后的向前传播或改变部分水舌的传播方向，一定程度上改变了破波能损率。