改进型RRT*算法的水下机器人三维全局路径规划

师颖慧，张 冰，赵 强

（江苏科技大学电子信息学院，江苏镇江 212003）

0 引言

自主水下航行器（Autonomous Underwater Vehicle，AUV）能够按照需求探测水下环境并自主完成作业任务。路径规划技术是自主水下机器人关键技术之一，指为到达某个目标或完成某个任务对所规划设备的航行方向、航行路线等进行预先计算、设定、优化的过程。路径规划技术在一定程度上标志着水下机器人智能化程度的高低。

水下航行器路径规划需要在三维空间中寻找可行路径，是一项非常困难和具有挑战性的任务。目前全局路径规划算法有Dijkstra算法、A*算法、RRT算法、粒子群优化算法（PSO）、蚁群优化算法（ACO）等。Dijkstra算法是典型的单源最短路径算法，用于计算一个节点到其他所有节点的最短路径，虽然其获得最短路径的成功率高、鲁棒性好，但在大规模复杂路径拓扑网络中，节点遍历和效率低下是其致命缺陷，所以不适合三维的空间环境；A*算法是求解静态路网中最短路径最有效的直接搜索解，也是求解其他问题的一种常见的启发式算法，优点是低成本、启发式最优解路径且在规划过程中可以及时中断和恢复，但A*算法是通过比较当前路径邻近网格的启发式函数值逐步确定下一个路径网格，当存在多个最小值时A*算法不能保证搜索到最优路径，即A*算法容易陷入极小值点，不适合解决三维空间中的路径规划问题；粒子群优化算法（PSO）是一种基于鸟类种群捕食和回归的启发式算法，在搜索的初始阶段收敛速度较快，但在搜索的后期收敛速度较慢；蚁群算法优点是可应用于水下三维路径搜索问题，其参数相对较少，不需要人工调整，但是收敛速度慢，容易陷入局部最优。几种全局路径规划算法各有优缺点，都能实现对全局避障路径的搜寻，但基本前提是要对环境空间进行路径建模，之后在已有路径基础上运用算法搜寻最优路径，Canny已经证明随着维数的增长这些算法速度会大大下降。针对这些问题，本文引入基于采样的随机搜索，如快速搜索树算法（Rapid-exploring random tree，RRT），在复杂的水面环境下，由于不需要提前对环境空间进行路径建模，更方便搜寻全局避障路径。RRT算法是基于采样的单一查询路径规划算法，其不需要对状态空间进行预处理，且搜索树能快速朝着未知的状态空间部分搜索。文献［9-13］指出，所有基于RRT 的方法几乎都是次优的，即使用RRT算法规划出的路径不是最优的，因此引入RRT*。RRT*扩展了RRT 求渐近最优解，即当样本个数趋于无穷时，它保证收敛于最优解。然而，水下环境的特点是障碍物很分散，包括地形障碍物和漂浮障碍物，这与地面上的障碍物不同。RRT*中全局均匀随机搜索导致搜索效率低、收敛速度慢、存储要求高，特别是在水下环境和高维空间中。

本文针对RRT*中出现的问题对其进行改进，提出NT-RRT*算法（正态采样、三角裁剪的快速扩展随机树的改进算法），利用正态分布的空间采样策略代替RRT*中的全局均匀随机采样，使算法具有目标偏置性，加快了算法的收敛速度。针对规划出的路径过于曲折、转角过多，不适合AUV 的实际运动情况，又引入基于三角不等式的几何修剪算法，在算法中用邻近节点的父节点代替临近点，然后与新加入的节点相连，使距离代价更小，规划出的路径更加平滑。仿真结果表明，改进的RRT*方法通过改变采样策略和减少节点数，提高了水下路径规划中的路径搜索效率和收敛速度，降低了路径代价，减少了路径的弯曲程度。

1 改进的RRT*算法

1.1 环境建模

本文利用栅格法将环境地图分为725×648格，每个格子不仅表示自身的像素信息，还用8 位二进制数表示其颜色信息，分别用不同颜色来标注障碍物区域和非障碍物区域。因为不同的颜色代表不同的RGB 值，这样在算法中很容易识别障碍物，对地图进行预处理，避免了算法执行过程中对路径进行避障距离检测，减少了算法的计算时间。

1.2 正态分布空间采样策略

假设环境空间为D，Dfree为环境空间中的无障碍区域，D为环境空间的障碍区域，q∈D为起始点，q∈D为目标点。

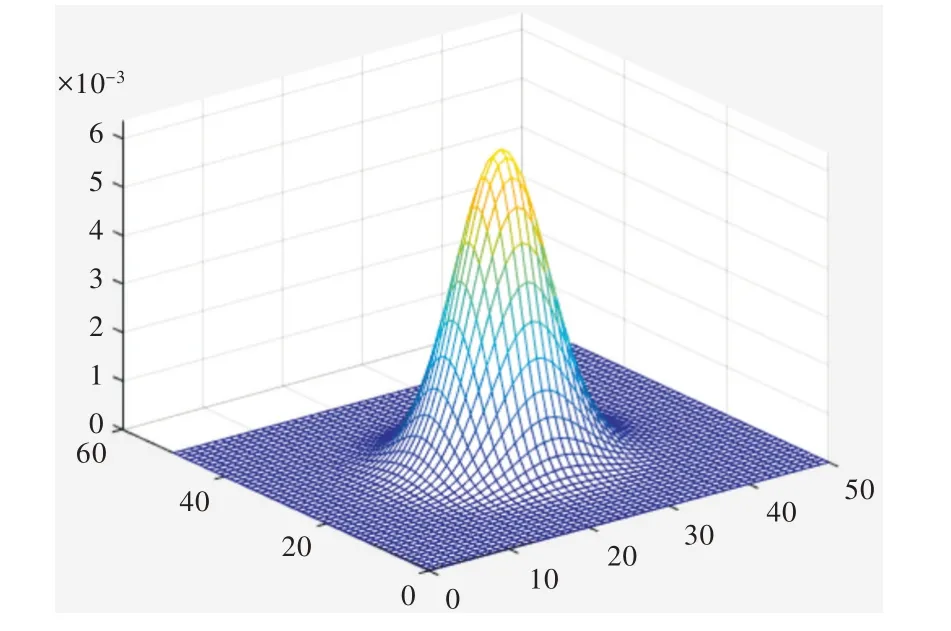
Fig.1 Two-dimensional normal distribution image with mean 25，25 and variance 25 and 25图1 均值25、25，方差为25、25 的二维正态分布图像

图1 中，空间中的点以均值25、25 为中心呈现正态分布，且数据的分布区间由标准差25、25 决定，说明通过设置正态分布函数的均值，标准差可以决定数据的分布情况。所以本文在算法中利用MATLAB 中的二维正态概率密度的离散函数对空间的点进行采样，使离散点符合以目标点为均值、目标点与起始点的大致范围设为标准差的正态分布，这样算法在空间中采的点就不是服从均匀分布而是以目标点为正态分布的最高点。从起始点到目标点均服从正态分布，从而使算法具有目标偏置性，加快了算法的收敛速度。改进后的N-RRT*（正态采样RRT*算法）详细内容见下面的N-RRT*算法步骤Algorithm 1，改进的RRT*方法描述如下：

函数Samplenodes 是二维正态采样点函数，其返回以采样点为均值，以起始点和目标的大致范围为方差，协方差为0 的离散点；函数FeasiblePoint 用来判断点是否在地图中或者是否与障碍物相碰撞；函数linepath 用来连接拓展的顶点和分支。

N-RRT*算法步骤如下：

1.3 基于三角不等式的几何修剪算法

RRT*算法在RRT算法基础上引入代价函数来优化规划出的路径，经过逐次迭代改善之前的路径，从而得到一条最优或准优路径。与RRT 不同的是，RRT*在扩展新节点时要分别计算最近邻点集合中的所有点到新顶点的距离，加上新顶点到起始点的距离作为路径代价，选择出一条最短路径，而RRT 是直接由起始点到最邻近点再到新顶点进行扩展，不考虑路径代价。

三角不等式的几何修剪算法（T-RRT*）在RRT*的基础上进行路径代价的改进，其不仅考虑邻近点集合中的点，还把临近点的父节点放入集合中，使其有共享父节点的趋势。图2、图3 分别是RRT、RRT*、T-RRT*三种算法的路径扩展方式，其基于q为算法的起始点，q为新加入的顶点，q为以q为球心、以r 为半径的球内的点，q为随机树中离q最近的点。

图4 中实线表示随机数原来的扩展路径，虚线表示重新选择父节点后的路径。由三角形中任意两边之和大于第三边定理可知，q到q的距离加上q到其父节点的距离（即图中黑色虚线所示）大于q到q父节点的距离（即图中黑色虚线所示），所以NT-RRT*算法计算路径代价时把q的父节点（图中黑色实心点）也考虑在内，在每一次迭代后计算出最小路径代价，并进行路径重连（即由红色实线代替黑色虚线的路径）。这种基于三角形不等式的定理，理论上会使更多的节点共享同一个父节点，重新连线的结果如图5 中红色实线所示。

Fig.2 Path extension mode of the RRT algorithm图2 RRT算法路径扩展方式

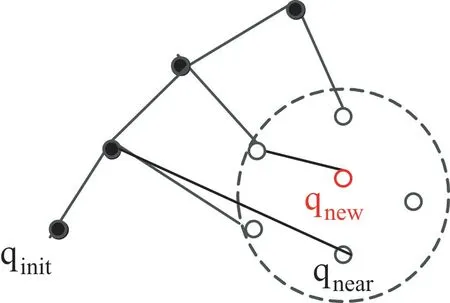
Fig.3 RRT* algorithm path extension图3 RRT*算法路径扩展

Fig.4 T-RRT* reselecting the parent node图4 T-RRT*重新选择父节点

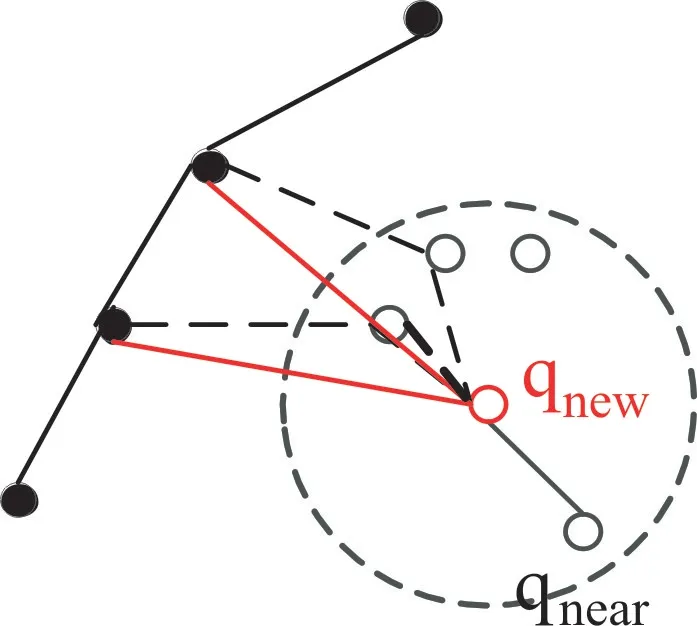
Fig.5 T-RRT* path reconnecting after selecting the parent node图5 T-RRT*选择父节点后路径重连

2 改进的NT-RRT*算法在海底环境下的仿真

水下环境有浮动及不平衡的地形两个障碍。本文对改进的RRT *在有浮动障碍和地形障碍的环境中进行仿真。仿真中利用MATLAB 建模，模型中将环境地图分为725×648 格，起始点格数设置为（193，305），目标点格数设置为（206，82）。仿真中，4个案例的采样节点都以红色圆点表示，扩展树的分支由红色直线表示，初始路径由黑色线表示。NT-RRT*算法如下：

使用MATLAB 形成的算法仿真图形如图6—图11 所示，坐标单位：m。

由图8 可知，在使用了正态分布的偏置采样策略后，随机树在扩展过程中只朝着目标点进行扩展，而不是像图6中均匀朝着四周扩展。由图9 与图7 对比可知，N-RRT*算法在进行路径规划时选择了一条障碍物更少的路径，且规划出的路径离障碍物更远，更有利于水下机器人在实际航行中安全前进。

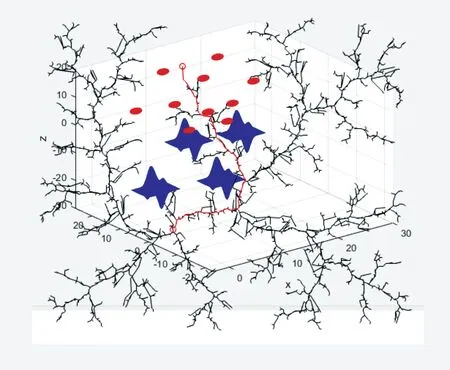
Fig.6 RRT* algorithm simulation图6 RRT*算法仿真

Fig.7 Specific route formed by RRT*algorithm simulation图7 RRT*算法仿真形成的具体路线

Fig.8 N-RRT* algorithm simulation图8 N-RRT*算法仿真

Fig.9 Specific route formed by N-RRT* algorithm simulation图9 N-RRT*算法仿真形成的具体路线

由图10 可知，NT-RRT*算法规划出的路径很平滑，唯一的一处拐角也离障碍物很远，水下机器人在实际操作中会更加简单。由图11 与图9 对比可知，NT-RRT*算法规划出了一条更加安全的路径，在此路径中水下机器人离障碍物很远，且规划出的路径几乎都是直线，不像图8 所示的弯曲较多。

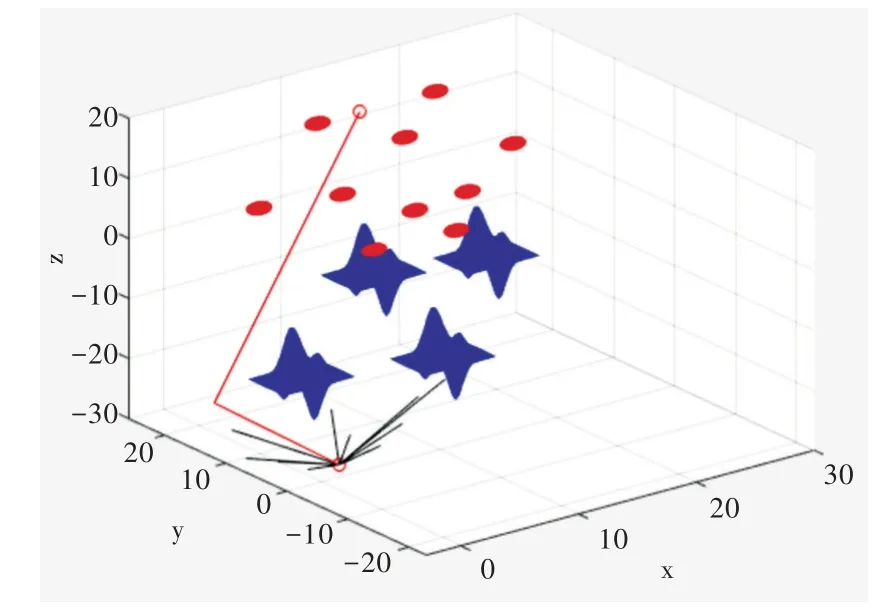
Fig.10 NT-RRT* algorithm simulation图10 NT-RRT*算法仿真

Fig.11 Final route formed by NT-RRT* algorithm simulation图11 NT-RRT*算法仿真形成的最终路线

由表1 可知，在相同步长下，N-RRT*算法所用时间是RRT*算法所用的时间的1∕10，NT-RRT*算法所用时间是RRT*算法所用的时间的1∕20，说明加入了正态分布的采样策略后提高了算法的收敛速度。N-RRT*算法路径长度相比于RRT*算法、N-RRT*算法减少了一倍，节点数减少为原来算法的约1∕7，说明加入基于三角不等式的几何修剪算法后减少了算法规划的路径长度和节点数。图11 说明NT-RRT*算法在3 种算法中路径光滑度最好，只有一个转折点，更能满足水下机器人在实际航行中的运动约束要求。

Table 1 Comparison of time and path length generated by the three algorithms under phase synchronization length表1 相同步长下3 种算法所用时间和形成的路径长度比较

3 结语

本文从空间采样策略和几何修剪算法角度改进RRT*算法，解决RRT*算法在路径规划时收敛速度慢、占用内存大、规划出的路径曲折性较大等问题。首先介绍了在RRT*算法基础上加入正态分布采样策略的N-RRT*算法，解决RRT*收敛速度慢、内存占用大的问题；然后在NRRT*算法基础上加入基于三角不等式的几何修剪算法——NT-RRT*算法，减少随机树在扩展过程形成的节点数，从而加快算法收敛速度，降低路径的弯曲度；最后在地形起伏、漂浮障碍物分散的水下环境中进行仿真。仿真结果表明，N-RRT*算法、NT-RRT*算法在收敛速度和路径长度方面优于RRT*算法，并且NT-RRT*算法收敛速度最快，路径规划所用时间最短。其规划出的路径离障碍物较远，安全性较高，路径非常平滑。

但是此算法还有不足，如没有加入AUV 在实际情况中所受的运动约束和动力约束影响因素，并且此算法的改进是基于先验环境信息。后续将利用传感器得到的信息构造动态环境模型，并将改进后的算法应用其中。