基于Copula函数方法的风险相关性实证研究

李伯华，赵宝福，贾凯威，吴津津

（辽宁工程技术大学 工商管理学院，辽宁 葫芦岛 125105）

0 引言

中国股市已进入高速发展时期，股票价格对于外部的信息冲击更为敏感，经常会出现这样的现象，一个板块的涨跌会影响到其他板块，或者说有些板块的涨跌会跟随敏感板块的变化而变动.中国证券公司较多，券商板块与整体股市的市场表现呈现出联动性.券商板块在某种程度上反映了市场的活跃程度，纪汉霖等[1]研究发现券商指数对上证指数走势的贡献最大.证券公司的专业优势和特殊社会职能使得投资者对券商板块的关注度更高，因此券商的投资动向和市场表现也被赋予更高的参考权重，并对于个人投资者投资决策产生影响.投资者采用跨板块投资的方式存在非理性行为和投机行为，板块间的联动效应引导市场的走向，也导致市场风险跨板块的流动.券商板块的波动对股票市场的波动存在很强的溢出效应与风险溢出性，导致风险跨板块流动以及市场中出现的一些跟风投资现象.券商板块的实际表现会有很强的投资暗示，那么券商板块能否引领整体股市的波动趋势呢？这个问题值得深入研究.

对金融市场内部的联动效应和波动溢出效应的研究是现代金融学研究的热点.对于金融波动与外溢问题的研究，BOLLERSLEV T等[2]首先应用了GARCH模型来研究金融资产价格波动的集聚性，之后很多学者也采用此方法来实证市场间的溢出效应.孙德山等[3]通过GARCH模型对深证综合指数收益率的波动进行了实证分析，发现深证综合指数收益率存在波动的集聚性和波动的非对称效应，进而验证了风险溢出理论.目前关于股票市场与板块之间互动关系研究的文献较少，大部分学者均以板块间或沪深市场间的关系研究为主.张良贵等[4]通过构建溢出指数来衡量中国股市行业间的波动溢出效应，研究结果表明中国股市板块间的收益与波动溢出存在影响关系.CHEUNG W等[5]利用线性回归模型研究了国内主板市场对创业板市场的溢出效应.金春雨等[6]通过研究发现不同行业板块之间的流动性溢出效应存在较大差异，但金融板块流动性变化对其他板块流动性具有显著正向溢出效应.戚逸康等[7]认为房地产板块与股票市场间存在显著的溢出效应与风险相关性.何红霞等[8]通过构建VECH-GARCH模型验证了雄安新区板块与主板市场间也存在显著的波动溢出效应和风险相关性.周亮[9]研究发现各行业间存在系统性风险关联.另外，李建勇等[10]、LI Y N等[11]、BONG H K等[12]、廖士光等[13]、周云龙等[14]均从各个角度对股票市场的内部板块的关系与风险相关性进行了探讨.其中，李成等[15]采用VAR-BEKK-GARCH模型对货币政策与股票市场间的溢出效应进行了实证分析.MACDONALD R等[16]也采用了类似方法对欧元区风险的溢出性进行了研究.

常用的风险相关性分析方法是VaR（Value at Risk），但存在一定的局限性，黄金波等[17]用非参数估计的方法对其做出了改进.继 ROCKAFELLER R T[18]等提出ES模型（预期亏损模型）和ARTZNER P等[19]构建了条件风险价值模型后，风险相关性的分析又有了新发展.宫晓莉等[20]以条件风险价值的方法测度金融机构间的风险溢出效应.李红权等[21]则采用Copula函数对金融系统做出风险相关性的评估.候叶子等[22]利用Copula-GARCH模型发现在股价上涨或下跌中，上海股市与深圳股市的收益与风险相关性有增强趋势.马梅等[23]也利用Copula函数得出了类似的结论.

经济发展离不开股票市场的支持，股票也是企业融资的重要方式.股票市场的非正常波动必然会引起实体企业的市值变化，进而影响到企业的发展，甚至会影响经济的走向.股市内部之间特别是板块间的影响更值得探究，特别是在全球经济受到疫情冲击时，券商的特殊作用也凸显出来，券商板块的非理性波动势必会给股市带来负面的影响和冲击.因此，探讨两者之间的波动性和风险性关联也具有很重要的现实意义.GARCH-Copula-CoVaR模型正逐渐应用在股票市场与板块间互动关系的研究中.因此，笔者通过构建GARCH模型刻画出2个时间序列的边缘分布，计算CoVaR值，再利用Copula连续函数进行相关性的实证分析，并进行回测检验，以揭示券商板块作用于整体股市的机理.

1 研究设计

1.1 VAR-BEKK-GARCH模型

研究券商板块对A股市场的影响情况，主要考察券商板块对整体股市间的溢出效应.溢出效应主要从两方面进行考察，一阶矩溢出（均值溢出）和波动溢出.

选取VAR-BEKK-GARCH模型来研究溢出效应.BEKK模型通过改进GARCH(1,1)模型，拓展了该模型的应用范围，可以用于多个市场之间的研究，同时模型的设定也解决了协方差矩阵非正定的问题，以及正负冲击的非对称性问题.采用的VAR-BEKK-GARCH模型表达式为

式中，yt为时间序列；a为常数向量；εt为假设服从条件正态分布的向量.yt、a、εt均为2×1维向量.vi(i=1,2,…,p)为估计系数，ξt-1为t-1期的信息集，Ht为条件方差-协方差矩阵.

式（1）可选用VAR模型来计算系数矩阵中元素的显著性，从而可以判断出券商板块与整体股市之间是否存在一阶矩溢出，券商板块的前期收益率是否能对整体股市起到一定的预测作用.

BEKK-GARCH模型通过矩阵相乘的方式解决了协方差矩阵非正定性的问题.BEKK-GARCH模型中的多元方差模型为

式（2）的展开式为

式（3）～式（5）中，h11,t、h11,t-1为主板市场的条件方差；h22,t、h22,t-1为券商板块的条件方差；h12,t、h12,t-1和h21,t、h21,t-1为券商板块和主板市场的条件协方差，可知h12,t与h21,t相等，h12,t-1与h21,t-1相等；ε1,t-1、ε2,t-2为券商板块和主板市场的均值方程的残差.

通过Wald检验来检验参数矩阵中各元素的显著性，用以验证波动溢出效应的存在性.Wald检验的原假设可假定为：b12=0，a12=0.当券商板块对主板市场的波动溢出效应不存在时，此原假设成立.反之，当主板市场对券商板块的波动溢出效应不存在时，原假设：b21=0，a21=0也成立.

1.2 基于Copula方法的条件风险价值

传统的风险溢出方法VaR，即风险价值，是基于自身风险的度量，而条件风险价值（CoVaR）由ADRIAN T[24]提出，实质上是基于某一金融市场的极端风险水平下对另一个市场的风险度量，风险溢出效应也是基于CoVaR方法而进行的研究，可以更准确地度量实际风险.Sklar提出的Copula 函数可作为联合两个边缘分布的连接函数，能够更方便地得出2个变量的联合分布函数.利用TGARCH模型可提取金融时间序列标准残差分布，再利用Copula函数考察2个变量的相关性和非对称性，并在此基础上进行后续的研究.

风险价值V1定义为

式中，α为置信水平.

条件风险价值V2可定义为

式中，ri，rj均为金融时间序列.

式（7）等价于

可得

可通过TGARCH模型拟合出标准残差分布.将标准残差经概率密度函数转化可得出

式中，Hj、Hi为时间序列rj、ri的标准残差的概率密度函数.

由Sklar定理，式（11）可推出

式中，C为Copula函数；

Copula函数由TGARCH模型拟合后提取标准残差，利用Copula函数进行联合分布检验进而求得.根据前人的研究，Copula函数可表达为

同时假设F(y1)和F(y2)可微且连续，C可确定唯一，同时令α1=F(y1)，α2=F(y2)，则可得到

一般根据时间序列特征选择Copula函数，由于金融时间序列的特殊性，金融风险的上下尾相关性等，选用阿基米德Copula函数中的Gumbel-Copula、BB7-Copula，以及t-Copula的拟合结果进行评价与比较，选取适合的Copula连接函数.

1.3 研究对象和数据选取

以2000年1月1日至2020年1月1日的上证综合指数以及券商指数为研究对象，见图1.

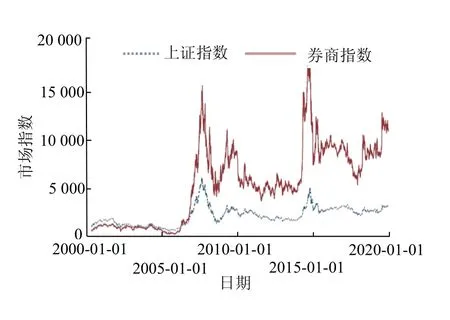
图1 上证综合指数与券商指数Fig.1 Shanghai composite index and brokerage index

采用Stata、Eviews和Winrats统计软件，数据来源于Wind数据库.选取上证综合指数为整体股市的代理指标.因其构成的公司已完成股改，能准确反映市场情况，券商指数的成分构成是由经营证券、基金、期货等业务的43家上市公司组成，能够精准反映券商板块的波动情况.

由图1可见，上证综指和券商指数的变动趋势基本一致，但是券商板块的波动更为剧烈一些.从时间节点上看，在上涨趋势中，券商指数先于上证指数开始上扬，而在下跌趋势中，券商指数的下降趋势晚于上证指数.在上涨与下跌阶段都存在变化时点不对应的关系，券商板块与整体股市间趋势间存在着不对称的引领关系.

因金融数据的特殊性，本文将这2个指数的原始数据进行取对数收益率的预处理，采用的公式为

式中，Pi,t、Pi,t-1分别为t时刻和t-1时刻的价格指数.

计算后，对数据进行统计分析，其基本特征见表1.

表1 指数对数收益率统计特征Tab.1 statistical characteristic of exponential logarithmic rate of return

因正态分布的数据偏度为0，峰度为3，本文将对比各样本区间中的数据与正态分布的偏差，所以进行J-B检验，结果见表1.可见，上证综合指数和与券商指数都呈现出尖峰厚尾的特征，并且拒绝了服从正态分布的原假设.以极值理论对此特征进行研究，并对二者进行ADF检验，显示2个数列均在1%的显著性水平上为平稳序列，结果见表2.

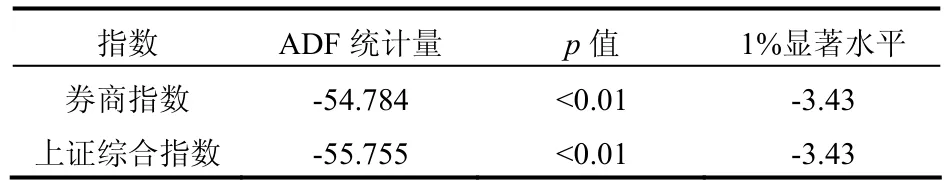
表2 指数对数收益率的平稳性检验结果Tab.2 result of stationary test of exponential logarithmic rate of return

2 实证分析

2.1 券商板块与整体股市之间均值溢出效应分析

通过建立以上证综合指数收益率和券商板块收益率2个序列的向量自回归模型来分析整体股市和券商板块之间的一阶矩溢出效应.依据AIC信息准则、SBIC信息准则、HQIC信息准则、LR检验统计量和最终预测误差（FPR）等标准，通过4阶滞后的VAR模型得出结果，见表3、表4.

表3 VAR模型阶数判断结果Tab.3 lags of VAR model

表4 格兰杰因果检验结果Tab.4 result of Granger test

由表4可见，券商板块与整体股市在95%显著水平上互为格兰杰因果关系，也就是说两个市场相互影响，券商板块的变动会引起主板市场的波动，而整体股市的波动也会带动券商板块的变动.在脉冲响应和方差分解上也得到相应的结果，所以二者间存在均值溢出效应.

2.2 券商板块与整体股市间波动溢出效应实证分析

建立BEKK-GARCH模型来验证波动溢出效应.y1和y2分别为上证综合指数和券商指数，对数据进行取对数的收益率处理后，进行LM检验，结果表明，2个序列在1%显著性水平上具有ARCH效应，可建立GARCH模型，估计结果见表5～表7.

表5 BEKK模型估计的均值方程结果Tab.5 mean equation results estimated by BEKK model

表6 BEKK模型估计的方差方程结果Tab.6 variance equation results estimated by BEKK model

表7 Wald联合检验结果Tab.7 result of Wald test

原假设1为H01：b21=0，α21=0，即上证综指与券商指数间不存在波动溢出效应.估计结果表明：上证综指与券商指数间存在显著的溢出效应.

原假设2为H02：b21=0，α12=0，即券商指数与上证综指不存在波动溢出效应.估计结果表明：券商指数和上证综指间存在波动溢出效应.

原假设3为H03：b12=0，α12=0，b21=0，α21=0，即券商板块与上证综指二者之间不存在波动溢出效应. 估计结果表明：上证综指与券商指数间均存在显著的波动溢出效应，且通过了Wald检验，在99%的置信区间内显著.

以上估计结果可以看出：①BEKK-GARCH模型的系数α11、b11、α22、b22在99%的置信区间水平上显著，说明上证综指与券商指数均具有明显的波动聚集性特征.②BEKK-GARCH模型中，系数b12在5%的显著性水平上显著，是由于大盘指数的走向仍然是投资者观测的风向标，上证综指对于券商指数波动溢出效应显著.③α21、b21在1%显著性水平上显著，券商指数对上证综合指数存在显著的波动溢出效应，因此α12显著表明券商板块的前一期的价格冲击会影响到整个股票市场，进而造成整体股市的波动；b12显著说明券商板块的当期产生波动对下一期的波动产生影响；从正负效应来看，券商板块的信息冲击削弱整体股市的波动性，券商板块的前期波动率能够增强整体股市的波动，但是新的冲击对整体股市的影响则更大，整体股市对于券商板块的冲击没有券商板块对整体股市的影响程度大.

券商板块的波动和变化能够显著地影响主板市场，券商板块一旦启动会带动整体股市的上涨，券商板块的剧烈波动也会显著影响到整体股市.因此券商板块对于整体股市来说具有非常显著的波动溢出效应，也具有引致股票市场波动的能力.这也说明国内股市在每一波行情中，均可以券商板块的发动程度作为参考指标，且事实上众多投资者都是以券商板块的投资动向作为投资决策的重要参考.

在2008年及2015年的股市动荡之后，股市的异常波动成为关注的焦点.关于股市的稳定以及对股市系统性风险的防范成为研究热点，而股市内部之间的风险联动也成为不可忽略的部分.

2.3 券商板块与整体股市的风险相关性实证检验

米先华等[25]研究发现风险补偿在不同行业间存在差异性，券商板块市值占到A股总市值的10%以上，由于券商的特殊地位和与上市公司的关联性，特别是2015年7月“股灾”后以汇金公司和中金公司为代表的“国家队”进入股票市场，并成为部分上市证券公司的股东，因此券商板块的投资方向和股价波动趋势受到更多投资者的关注.券商板块也成为了股市的风向标，券商板块的活跃程度与整体股市密切相关，在基本面信息一致的情况下，券商板块与整体股市间存在共同变动和相互作用，因而应当将券商板块与整体股市的风险相关性进行研究和分析，以深入揭示两者之间的内在关联.

2个时间序列通过了平稳性检验，通过GARCH模型拟合后，经Ljung-Box检验p值均大于0.10，存在ARCH效应，符合金融数据的波动集聚性特点. 整体股市和券商序列残差密度函数见图2.

图2 整体股市和券商序列残差密度函数Fig.2 residual density function of the whole stock Marketand rokerage block

由图2可看出标准残差属于t分布，存在尾部不对称现象，残差分布具有尖峰厚尾的特征.券商板块与整体股市间的信息杠杆现象见图3.

图3 两变量信息冲击Fig.3 informatin impact

图3 中，横轴正值代表好消息冲击，负值代表坏消息冲击，在市场消息利好时上涨的速度要小于股市处于利空时下跌的速度，这与中国现实情况相符.根据2个时间序列标准残差的边缘分布，对其进行概率积分转换，再用K-S检验变换后的序列是否服从(0,1)分布.经检验，K-S值均大于0.05，表明符合假设，(0,1)分布可以较好地拟合2个序列的条件边缘分布.利用R软件对3类Copula函数进行估计，t-Copula函数具有尾部相关性，Gumbel-Copula函数也能描述金融市场间的尾部相关，BB7-Copula函数也可以刻画变量间的上下尾相关性，因此经过模型计算后可得到结果，在实际结果中整体股市与券商板块的时间序列变量更倾向于t-Copula函数，表8为不同模型评价结果.

表8 3类阿基米德Copula函数估计结果Tab.8 estimate result of the three Copula functions

根据信息准则AIC、信息准则BIC可见，采用t-Copula函数的估计结果更贴合实际.计算条件风险价值见图4.

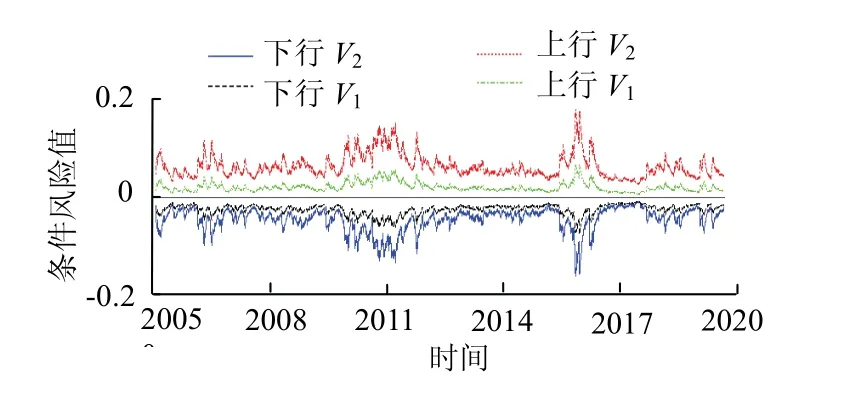
图4 t-Copula-V2波动Fig.4 volatile of t-Copula-V2

由图4可见，券商板块对整体股市存在很强的风险相关性.上行风险相关性高于下行风险相关性，券商板块与整体股市间的风险依存性很高，且存在非对称性.也正如市场表现，券商板块整体上涨时能带动整体股市趋势上扬，而在下跌中并不如上涨时期的引领作用显著.券商板块在整体股市的走势中存在不对称的引领作用，与平时观察到的现象一致，券商板块整体上涨会认为是“牛市”起点，而券商板块整体下跌则不认为整体股市下跌的开始.

对t-Copula分布下的条件风险价值CoVaR进行了回测，通过Kupiec检验来验证其准确性，结果见图5、图6.

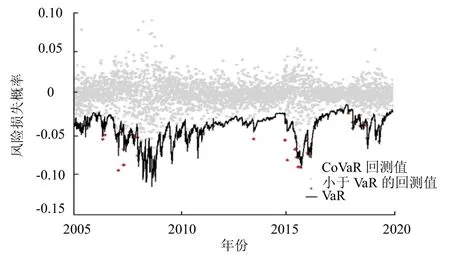
图5 整体股市对券商板块的CoVaR回测Fig.5 CoVaR back to test for the whole stock maket to securities dealerssector

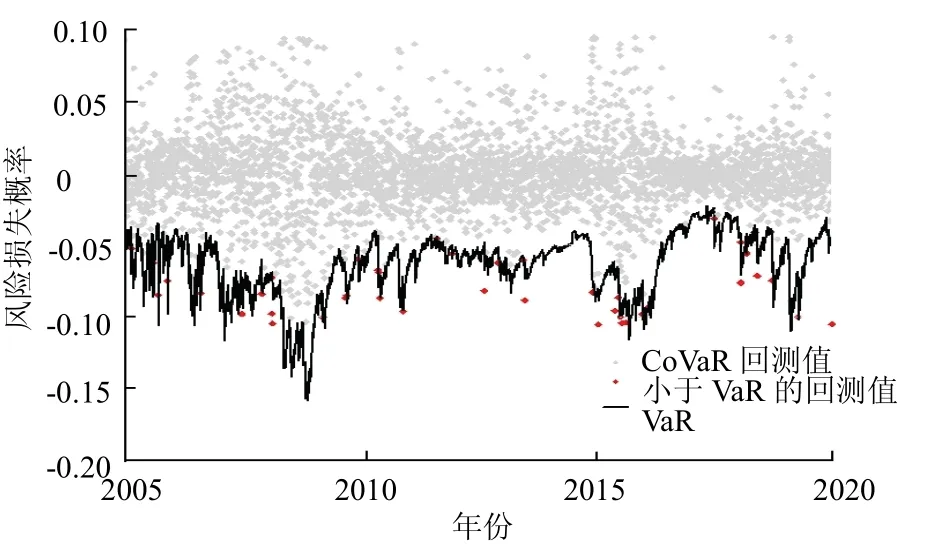
图6 券商板块对整体股市的CoVaR回测Fig.6 CoVaR back to test for securities dealerssector to the whole stock maket

由图5、图6可见，整体股市与券商板块间存在着风险性关联性，券商板块的波动与股市的稳定有很大相关性.

CoVaR回测检验分析结果见表9.

表9 CoVaR回测检验分析结果Tab.9 result of back to test

由表9可见，t分布在5%的显著水平上，统计量均小于3.481，说明样本的风险价值与条件风险值的测度效果很好，能够反映出两者的风险特征.在受到信息冲击时，券商板块与股市存在着风险关联性，同时也表明中国股市存在信息反应的不对称性，也就是信息杠杆，利好消息与利空消息对股价波动的影响程度不同，利好消息对股价波动的影响程度不如利空消息的影响程度大，呈现出不同的斜率变化.另外由图5、图6可见，券商板块对于整体股市的风险溢出波动更为剧烈，整体股市的波动对于券商板块的风险溢出性明显小于券商板块对整体股市的影响程度，因此也证实了在近几年的股市交易中投资者对券商板块的关注度较高.券商板块的风险波动能够影响到整体股市的波动，一方面是因为券商在股市系统中所处的特殊地位和信息优势，能优先获取到一些信息和动向，另一方面也是由于券商的股东结构，一些券商具备国有的背景，汇金公司与中金公司的持有背景往往也起到了一定的示范效应.

3 结论

（1）本文从理论和实证的角度分析了券商板块对于A股市场的溢出效应，通过建立VAR-BEKK-GARCH模型实证了券商板块对A股市场的溢出影响，揭示了两者之间的传导机制.券商板块对整体股市存在波动溢出效应，解释了中国股市在上涨行情和下跌行情中，常常出现由券商板块引领趋势的现象.证实了投资者将券商板块视为股市风向标的原因，整体股市的波动也对券商板块存在显著的溢出影响.

（2）金融市场间存在风险传递的现象，股市内部更是如此，风险跨板块流动.在考察券商板块与整体股市间的风险相关性时，通过对券商板块与整体股市日收益率标准残差的边缘分布构建联接函数Copula，搭建了Copula-GARCH-CoVaR风险溢出模型，分析了券商板块与整体股市的风险相关性.券商板块与整体股市间存在着风险流动性，且券商板块的风险溢出要大于整体股市对券商板块的风险溢出，也说明国内投资者对券商板块的关注度较高，赋予券商板块的参考权重较大.股市系统内部风险相关性显著.引领作用存在非对称性，说明券商板块在股市的上涨中起到引领作用，但在下跌过程中的引领作用没有上涨过程中显著.投资者特别是个人投资者如果以券商板块的动向来研判股市的大势，从而作为投资决策的重要参考时，会存在一定的判断误差.

综上所述，应当关注券商板块的波动情况，券商占有市场份额较大，而目前证监会的监管重点在上市公司上，应加强对券商的监管，规范券商的投资行为，重视券商板块的正向引领作用，注重风险的管理以减少系统性风险的发生.