考虑同类订单合并和应急订单干扰的生产调度优化

刘天昊，唐 亮，靳志宏

（大连海事大学 交通运输工程学院，辽宁 大连 116026）

0 引言

20世纪的主流生产模式为少品种、大批量模式，然而进入21世纪以来，企业生产已经逐渐转变为多品种、小批量的模式，若生产时计划安排不合理，会导致产品交货期延长，很大程度上影响制造商的经济效益.此外，同类产品订单的合并往往具有合并效益，能够减少调整时间和成本. 因此，研究考虑合并效益的生产调度有利于提高制造商应对不同类型订单的能力，从而提高盈利水平.与此同时，制造商往往面对突发应急订单的干扰，如何针对这种干扰提出有效合理的应对策略，构建重调度模型变得尤为重要.

生产调度是供应链调度的内部环节，是经典的组合优化问题.组合优化问题的研究起源于20世纪50年代，自JOHNSON S M[1]解决了两台机床的流水线生产调度问题之后，研究者们综合应用数学、运筹学等来处理生产调度问题，并且取得了丰硕的成果.其中CONWAY R W等[2]关于生产调度的研究开创了调度研究的理论基础. 20世纪90年代，随着智能算法在生产调度方面的推广应用，国内开始广泛研究调度问题，主要采用扰动分析和极大代数方法对制造系统的性能指标进行参数变化的敏感性分析，并以此为基础对系统的运行进行优化.刘瑞华等[3]针对柔性制造系统中特殊的BEDS排队网络，采用极大代数方法建立模型，同时分析了系统的稳定性.姜思杰[4]在对基于GA和TS的最小平衡算法及其在FMS的应用研究中，通过运用数学规划的方法把排队网络用于FMS. 但是，排队网络只能分析生产率、平均时间等，无法考虑企业的其他资源. 廖强等[5]针对一个大的半导体车间提出了一种基于交货期及缓存优先级的分布式调度算法.孙靖等[6]针对生产信息不完全共享的情况，为解决大规模的供应链的动态调度问题，提出了基于蚁群算法的多企业交互调度模型，通过企业代理之间的反复、自动交互，对订单任务分配及合作时序进行协调. 王凤等[7]放宽了对于生产调度问题的一些假设，利用图论理论建立了基于设备组合的数学模型，并基于蚁群算法的思想给出了求解方法，最后通过实例进行了验证.

在应急订单干扰下的重调度方面，方剑等[8]针对Job Shop调度问题提出基于工件的滚动调度方法，主要探讨滚动窗口的确定方法，以及怎样进行再调度以保证生产的连续性. YAMAMOTO M等[9]提出三阶段的重调度策略，首先根据车间当前信息在新调度开始之前生成预调度方案，每当有新工序开始加工或者工序加工完毕时，对比实际调度与预调度方案之间的偏差，最后根据系统与预调度方案的偏差对原方案进行修订，对未加工工件进行重调度. ABUMAIZAR R J等[10]提出一种重调度算法，当扰动发生时仅仅重新调度那些直接或间接受扰动影响的工件，减少了由于扰动引起的生产周期增加以及与初始调度的偏差, 效率和稳定性都较好. 李琳等[11]提出一种基于事件驱动的自适应动态调度方法，采用改进的启发式受影响操作重调度算法来确定调度中的受影响操作并对其做出相应的局部调整，从而以一种自适应的方式快速而平稳地完成虚拟生产系统的动态调度. 张国辉等[12]结合滚动窗口机制，采用基于周期和事件的混合驱动策略，运用Memetic算法对每个滚动窗口工件集进行重调度，改进后的基准实例验证了该策略的有效性. 上官春霞等[13]对分级模型提出改进的修复约束满足算法（修复法），并以90个作业车间标准算例为基础，设计了重调度算例，与第二代非支配排序遗传算法优化结果进行了对比，结果表明在相同运行时间下，所提算法更具优越性.

综上，现有研究内容主要采用生产周期最小化等指标来评价调度方案的优劣，但是较少有文献同时考虑具有合并效益的生产费用、工序调整费用、延期成本等，以及进一步考虑应急订单干扰下具有多目标的重调度模型、最小化生产扰动等。

因此，本文考虑同类产品订单合并，分析生产成本、半成品库存成本、设备调整成本，以及延期交货惩罚成本等四类成本，建立生产调度优化模型. 根据生产中的实际情况，建立应急订单干扰下的生产重调度模型，对两种应急订单干扰下的重调度进行分析.

1 考虑同类订单合并的生产调度模型

1.1 问题描述

生产调度中最普遍的问题可以描述为：设N个产品在M台设备上加工，每种产品均可以按照任何一种可能的顺序进行加工，因此可行调度方案很多，需要从中选择最优的方案. 本文建立的考虑合并效益的生产调度模型见图1，主要包括以下因素：①生产过程产生的基本生产费用，考虑到同类产品不同订单，以及是否进行组合生产，确定最优组合生产成本函数；②不同产品在不同订单情况下会出现半成品等待过程，产生一定的半成品库存费用；③不同类型的产品在同一设备上先后生产加工时，由于所使用的机器设备工序不同，会产生机器调整费用和调整时间；④若产品滞后于交货期完成，影响到企业的客户服务水平和销售业绩等，则会产生相对较高的延期惩罚费用.

图1 生产线费用描述Fig.1 production line cost description

调度的目的是确定每个订单的加工顺序、每台设备上产品的加工顺序和产品在每台设备上的开工时间，以保证产品生产在最晚交货期前完成，从而使产品的综合成本值最优或近似最优.

1.2 模型假设

在加工过程中，为了尽可能地满足实际情况，现做出如下假设和约束.

（1）同类产品不同订单可以考虑选择组合生产，一旦选择组合生产将一直保持到加工完成.

（2）一台设备一次只能加工一件产品，一件产品只能在一台设备上加工一次.

（3）任何一件产品只有在前一道工序加工完成后才能进入下一道工序，且一旦开始就不能中断，不考虑工序之间的运输时间.

（4）若订单到达某一工序时，该工序机器设备正在处理其他订单，则产生半成品库存费用，按订单批次计算，且与存储时长成正比.

（5）设备在加工不同产品之间进行切换会产生不同的设备调整费用.

（6）只有当产品到达某一工序后，才开始进行工序切换的设备调整，订单产品在不同工序之间切换时间纳入半成品库存时间.

（7）制造商完成产品时不考虑成品库存费用，但是晚于最晚交货期限会产生延期惩罚费用，按订单批次计算，且与延迟时长成正比.

1.3 模型建立

根据以上假设，构建考虑合并效益的生产调度模型. 在车间作业生产模式下，每类产品有不同的加工顺序，每道工序有多台不同的设备可供选择，一个订单在一道工序上只能选择其中一台设备加工. 如果产品交付客户的时间超过最晚交货期，则会影响企业的服务水平和订货商收益，因此需要对延期交货进行费用惩罚.

（1）模型参数及变量

k,k'=1 ,2,…,N（o或No,c） ：订单号.

l,j= 1,2,… ,：工序号（j是l的紧前工序号）.

m= 1,2,… ,：设备号.

i= 1,2,… ,Nl,m：每个订单在每台设备上的加工顺序.

No：订单数量.

Nk：第k个订单的产品总量.

Nl,m：第l道工序上第m台设备上加工的订单数量.

tk,l,m（ 或tk,j,m）：第k个订单每件产品在第l（或j）道工序的第m台设备上加工的时间.

Wl,m：第l道工序的第m台设备的单位运行费用.

ck,l,m,i：若第k个订单在第l道工序的第m台设备上第i个加工为1，其他情况为0.

Nc：需要合并生产的总订单数.

No,c：同类产品合并生产之后的订单数.

zk,l,m：第k个订单在第l道工序的第m台设备上加工时需要调整设备为1，无需调整为0.

（2）调度模型

①生产费用目标函数

根据以上模型假设研究和符号约定，调度模型的生产成本费用为

式中，第一部分表示没有合并生产的订单(No-Nc)的生产费用，第二部分表示合并生产的订单的生产费用，与合并生产系数相关.

②调整费用目标函数

若工序需要调整，设备产生调整费用，调度模型的机器调整费用为

式中，第一部分为没有合并生产的订单(No-Nc)的设备调整费用，第二部分为合并生产订单的设备调整费用.

③半成品库存费用目标函数

工序调整的时间包含于产品的半成品库存时间中，调度模型的半成品库存费用为

式中，第一部分表示没有合并生产的订单(No-Nc)的半成品库存费用，第二部分表示合并生产的订单的半成品库存费用.

④延期惩罚费用目标函数

产品加工完成时间若晚于最晚交货期则产生延期惩罚费用，调度模型的延期惩罚费用为

综合上述4种费用函数可以得出调度模型为

约束条件为

式（5）为目标函数，即调度模型成本最优；式（6）表示每件产品的加工工序先后顺序约束；式（7）表示在l工序上的第m台设备的第i个加工的产品只能有一个；式（8）表示订单k在l工序上第m台设备上加工的次序只有一个；式（7）和式（8）共同表示出每一道工序上选择某一设备上加工的所有产品顺序约束；式（9）表示各工序每台设备上加工不同订单产品的开始时间先后顺序约束；式（10）表示每件产品在某一台设备上开始加工时间与在该设备上加工时间之和等于该产品在该设备上的完成时间；式（11）为开始时间和结束时间约束.

1.4 算例实验

（1）制造商数据设计

假设制造商可以生产多种产品，产品可以在本厂6道工序中的某些设备上完成加工.制造商所拥有的设备见图2.

图2 制造商设备Fig.2 manufacturer's equipment

如图2所示，制造商设备4有两种不同的设备可供选择，加工成本与时间各有不同. 假设产品在加工过程中按照从M1到M6的顺序进行，但并不是全部工序都要经过. 考虑产品的生产成本函数和生产成本系数，由于本实例属于虚拟实例，此处假设设备运行的单位费用恒定，见表1.

表1 设备运行费用Tab.1 equipment operation cost

（2）客户订单数据设计

假设该制造商共接到客户1、客户2、客户3、客户4、客户5的订单，分别为订单A、订单B、订单C、订单D、订单E，其中订单A、订单B、订单C为同类产品，即共有5个订单，3种产品. 每个订单都有各自的最晚交货时间，考虑到制造商自己公司的资金和库存问题，设定加工完成即交货，推迟交货则制造商赔付相应的违约金（延期惩罚）.各个订单产品的数量、约定的最晚交货时间、半成品库存费用，以及延期惩罚费用见表2；3种产品的加工工序见图3、图4、图5. 由于生产的产品类型不同，假设机器设备在产品切换调整时，对应不同产品的调整时间不一致，3种产品在各自工序上的加工时间和对应设备的调整时间见表3～表5.

表3 订单A、B、C产品加工时间及设备调整时间、费用Tab.3 processing time, equipment adjustment time and cost of orders A, B and C

表5 订单E产品加工时间及设备调整时间、费用Tab.5 processing time, equipment adjustment time and cost of order E

图3 订单A、订单B、订单C产品工序Fig.3 product process of orders A, B and C

图4 订单D产品工序Fig.4 product process of order D

图5 订单E产品工序Fig.5 product process of order E

表2 产品相关信息Tab.2 equipment operation cost

（3）仿真结果

通过CPLEX软件进行求解，分别得出5个订单在：①订单A、订单B、订单C不合并时；②订单A、订单B合并时；③订单A、订单C合并时；④订单B、订单C合并时；⑤订单A、订单B、订单C合并时的调度甘特图，见图6～图10，调度结果见表6，各类情况费用对比见表7.

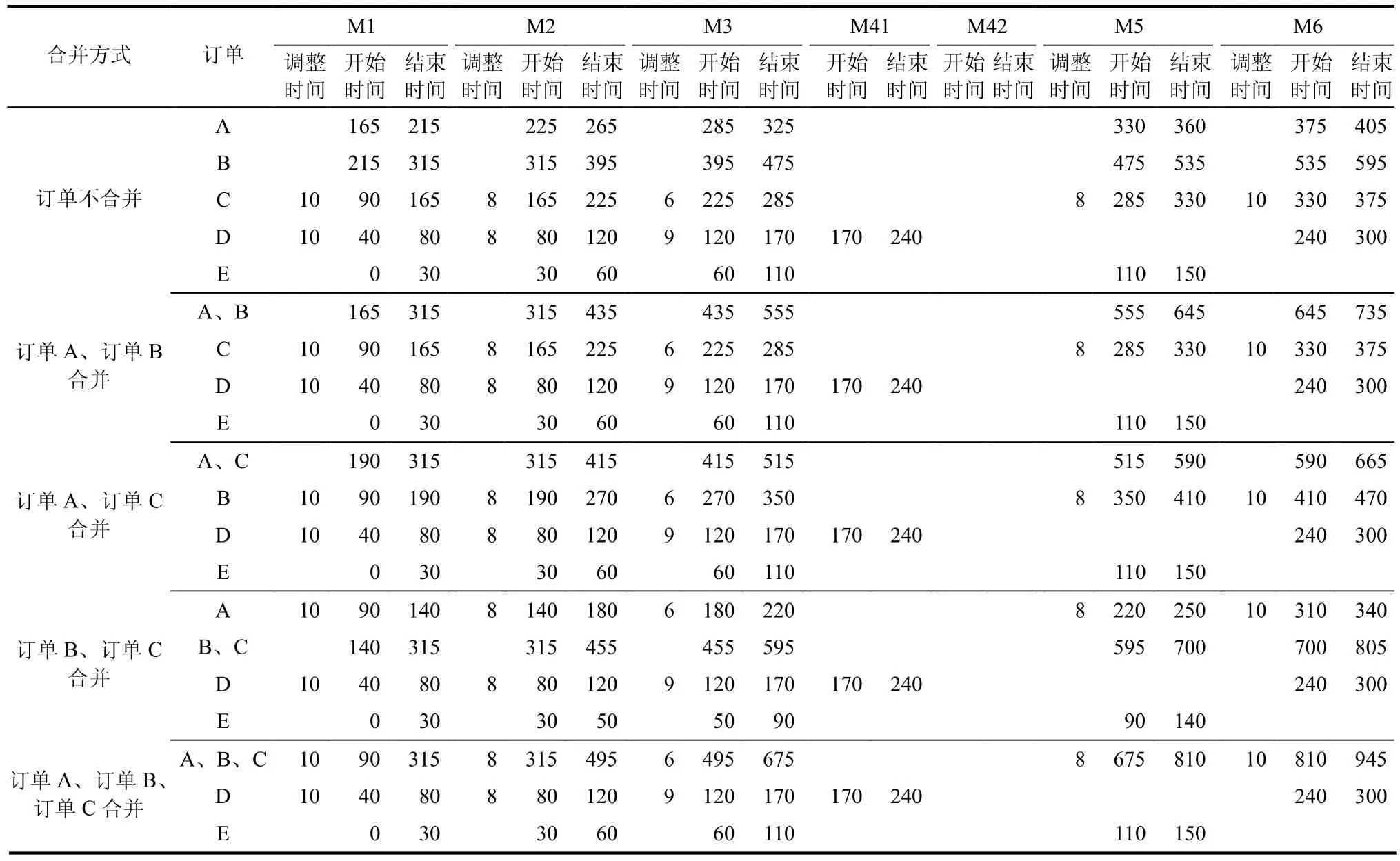
表6 开始时间、结束时间及调整时间运行结果Tab.6 results of starting time, ending time and adjustment schedule h

表7 各类情况费用对比Tab.7 comparison of costs in various situations 元

图6 订单A、订单B、订单C不合并生产Fig.6 production of orders A, B and C without merger

图7 订单A、订单B合并生产Fig.7 combined production of orders A and B

图8 订单A、订单C合并生产Fig.8 combined production of orders A and C

图9 订单B、订单C合并生产Fig.9 combined production of orders B and C

图10 订单A、订单B、订单C合并生产Fig.10 combined production of orders A, B and C

（4）结果分析

由表6和表7可知，订单A、订单B、订单C不合并时，总成本费用为3905元；订单A、B合并时，总成本费用为3708元；订单A、订单C合并时，总成本费用均为3732.5元；订单B、订单C合并时，总成本费用为3743.5元，以上这4种情况所有订单均未超期，能按期交货.而订单A、订单B、订单C合并生产时，总成本费用为9109.5元，此时订单A超期145 h，订单C超期45 h，导致总成本费用相比其他4种方案差距较大.

通过本次实例仿真可以证明考虑合并效益的生产调度模型的有效性与可行性.从上述5种调度甘特图可以看出，订单基本上按照一定的固定顺序生产，可以为企业考虑是否继续接受订单提供决策依据.

2 应急订单干扰下的生产重调度

2.1 问题描述

在实际生产中，应急订单到达、订单撤销、机器故障等突发干扰情况常常导致原生产调度执行效率低下，甚至不再可行. 应急订单的到达是一种常见的干扰，一旦发生便需要制造商重新安排调度方案，从而保证低成本、高效率地完成生产.重调度的原则是在尽量小地牺牲调度性能的同时保证调度的稳定性，有效地控制或缩小重调度与原调度之间的偏差程度.

本文将各调度目标进行合理简化，从任务完工时间、生产成本等方面建立重调度窗口内的优化模型.优化设计目标为：确定每一个任务的每一道工序在某一具体时间开始在设备上加工，使生产成本、扰动、完工时间权重和最小.

2.2 模型假设

在重调度过程中，为了尽可能地满足实际情况，现做出如下假设.

（1）每个订单在固定时刻只能在一台设备上加工，任何订单没有强占加工的特权.

（2）需要重调度时，正在加工的工序不受影响，继续加工直到该工序完成.

（3）应急订单到达干扰在初始调度生成后至多发生一次（即单一应急订单干扰）.

（4）一旦出现应急订单到达干扰，有且仅有一个应急订单亟待加工[14].

2.3 模型建立

（1）模型参数及变量

Ｗk：总成本.

Lk：重调度时预调度方案中任务k尚未完工的工序数.

tkl(tk′l)：预（重）调度方案中任务k的第l道工序的开工时间.

dk：每个任务的独立交货期.

Nkv：每个任务包含的相同类型零件数量.

（2）重调度模型

目标函数为

约束条件为

式（15）表示完工时间约束；式（16）表示动态扰动约束；式（17）表示加工时间约束.

2.4 实例仿真

根据上述模型和应急订单到达的情况，现假设应急订单F与订单E为同一类产品，应急订单G与订单D为同一类产品，它们的交货时间及延期惩罚费用如表8，其他各项数据分别和订单D和订单E相同，详见表4、表5.另外，这两种应急订单干扰下的重调度均是在订单A、订单B、订单C不合并的情况下进行分析的.

表4 订单D产品加工时间及设备调整时间、费用Tab.4 processing time, equipment adjustment time and cost of order D

表8 订单F、订单G产品相关费用信息Tab.8 product cost information of order F and order G

（1）应急订单F干扰下的重调度

假设应急订单F在200 h时到达，此时M1工序上的订单A、M2工序上的订单C、M41工序上的订单D均正在加工，因此要等现有工序加工完成之后才能进行重调度. 由于订单A、订单C、订单D的完工时为240 h，因此重调度只考虑在此以后的加工，除订单D继续按M6加工外，其余订单的加工工序流程见图11～图14.

图11 订单A产品工序Fig.11 product process of order A

图12 订单B产品工序Fig.12 product process of order B

图13 订单C产品工序Fig.13 product process of order C

图14 订单F产品工序Fig.14 product process of order F

在模型中可以看出，目标函数分为以下部分：①使最晚加工完的订单结束时间最短；②使加工的总成本最小，其中总成本又分为生产费用、设备调整费用、半成品库存费用和延期惩罚费用，考虑急件到达前的加工费用；③使重调度方案与原调度方案中各订单的开工时间差的绝对值最小.分别侧重于完工时间、总成本以及动态扰动三方面的运行结果见表9、表10.

表9 应急订单F干扰下开始时间、结束时间及调整时间对比Tab.9 comparison table of starting time, ending time and adjustment schedule under the interference of emergency order F h

表10 应急订单F干扰下整体完工时间、总成本费用及动态扰动对比Tab.10 comparison table of overall completion time, total cost and dynamic disturbance under the interference of emergency order F

由以上结果可以看出，当侧重于完工时间约束时，结果与侧重于动态扰动约束时一样，整体完工时间均为660 h，总成本费用均为6277元，动态扰动均为681 h，此时应急订单F均超期12 h，其他订单均未超期.而侧重于总成本时，整体完工时间也是660 h，但是总成本费用为4969元，动态扰动为1113 h，此时所有订单均未超期.

（2）应急订单G干扰下的重调度

假设应急订单G在200 h时到达，由于应急订单G与订单F的插入时间一样，因此订单A、订单B、订单C、订单D这四种订单的产品工序图与分析应急订单F插入时一样，因此这里只给出应急订单G的产品工序图（如图15），分别侧重于完工时间、总成本以及动态扰动三方面的运行结果见表11、表12.

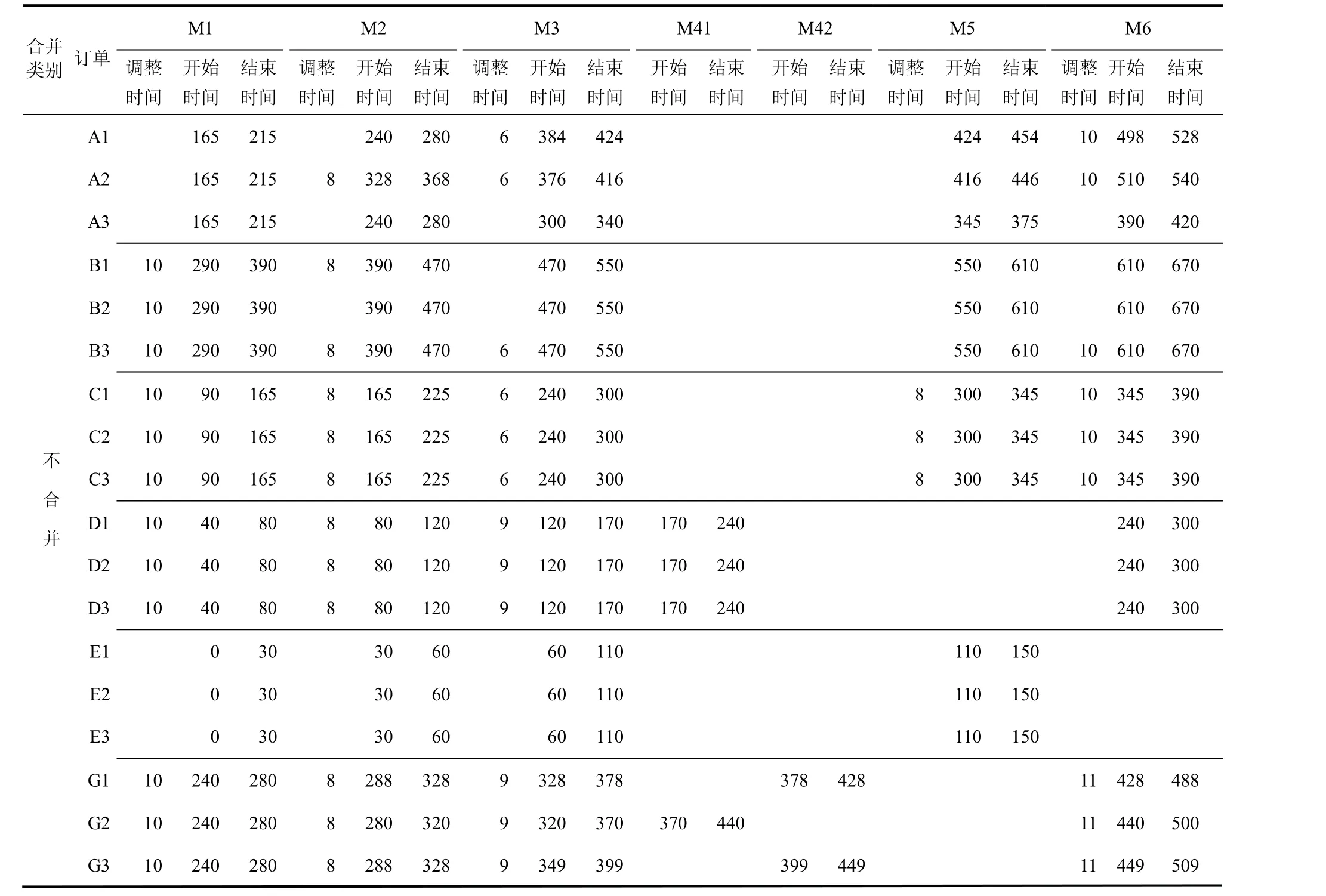
表11 应急订单G干扰下开始时间、结束时间及调整时间对比Tab.11 comparison table of starting time, ending time and adjustment schedule under the interference of emergency order G h

表12 应急订单G干扰下整体完工时间、总成本费用及动态扰动对比Tab.12 comparison table of overall completion time, total cost and dynamic disturbance under the interference of emergency order G

图15 订单G产品工序Fig.15 product process of order G

由以上结果可以看出，当侧重于完工时间约束时，应急订单G在工序M42上加工，整体完工时间是670 h，总成本费用是5389元，动态扰动是751 h，此时各订单均未超期；侧重于总成本时，应急订单G在工序M41上加工，整体完工时间是 670 h，总成本费用是5355元，动态扰动是835 h，此时各订单均未超期；侧重于动态扰动约束时，应急订单G在工序M42上加工，整体完工时间是 670 h，总成本费用是6223元，动态扰动是480 h，此时应急订单G超期9 h，其他订单均未超期.

综上所述，考虑生产中的实际情况，通过实例对应急订单的干扰进行了分析，并分别将完工时间、总成本、动态扰动作为侧重点进行对比研究，为调度策略的进一步优化提供了重要支撑.

3 结论

（1）在考虑订单合并的基础上，建立了考虑生产费用、设备调整费用、半成品库存费用及延期惩罚费用的生产调度优化模型.通过仿真算例得出订单合并前后的成本差异，验证了模型的有效性，为制造商企业提供了决策参考.

（2）建立了应急订单干扰下的重调度优化模型，从完工时间、总成本费用、动态扰动等方面进行了对比分析，为制造商提高抗击突发干扰的能力提供了依据.

（3）进一步的研究将聚焦于订单合并与应急订单的集成调度，同时针对应急订单的多重干扰、相继出现的情形进行深入研究.