基于多尺度分析的遥感变化检测

谢贵臣，何浩，邢栋

(新疆大学建筑工程学院，新疆 乌鲁木齐 830047)

1 引 言

遥感变化检测是遥感影像分析中重要的应用之一，在土地管理、环境监测、农业林业管理、灾害救援与治理等领域有广泛的应用[1]。尺度在遥感影像分析中具有重要意义，在同一景影像中同类地物由于自身大小不同，而无法采用单一分析尺度进行分析。因而最佳分割尺度的确定成为面向对象变化检测的关键问题之一。

针对变化检测中的尺度问题，蔡怤晟等[2]提出一种结合特征选择的CVA多尺度遥感影像变化检测方法，一定程度上提高了变化检测的准确性。刘红超等[3]提出一种面向类型特征的自适应阈值遥感影像变化检测方法，一定程度上减弱物候期对变化检测的影响，且具有更好的稳定性。徐俊峰等[4]提出一种利用慢特征分析的特征级多尺度融合变化检测方法，在检测精度和自动化程度方面更具优势。王超等[5]结合阴影补偿因子，设计了一种基于D-S证据理论的决策级多尺度融合策略，该方法较好地解决了阴影引起的错检问题。薛昱晟[6]在地理国情监测中采用了多尺度分割方法，检测结果优于单一尺度分割的结果。已有的多尺度分割变化检测方法常将各尺度单独分析再融合，忽略了尺度间隐含的上下文信息。针对此问题本文提出一种多尺度分析的变化检测方法。

2 方法

首先，对双时相影像进行多尺度分割，将前后时相的分割结果叠置，生成子对象；其次，以大、中、小尺度下的子对象为基本分析单元，计算影像光谱特征的结构相似性测度，得到某一尺度下子对象的变化强度图；最后，对各尺度下提取的变化强度信息，进行多尺度变化信息模糊融合，得到最终的变化检测结果。具体流程如图1所示。

图1 多尺度分析变化检测流程

2.1 影像分割与子对象生成

利用ESP2工具[7]我们可以获得目标地物提取的几个最佳分割尺度。再借助eCognition软件，按照最佳分割尺度，利用影像光谱特征，对前后两时相影像分别进行预分割。在双时相影像中同一未变化地物受到成像条件差异的影响，分割边界通常并不一致。而双时相影像中变化地物的边界本身也不一致。这些不一致的分割边界对后续的变化检测工作带来一定的困难。为此，本文将前后时相影像分割结果进行叠置进一步生成子对象，以此解决分割边界不一致问题。后续的分析处理中以子对象作为基本分析单元。

2.2 变化强度图构建

采用影像的光谱特征结构相似度来描述双时相影像间的差异性。结构相似度(Structural Similarity，SSIM)由Wang Zhou等[8]首次提出，主要用于图像质量评价。SSIM通过两向量的均值、方差、协方差来评定向量间的相似性程度，是一种基于结构信息的相似度评价方法，其定义为：

Vk=SSIM(T1，T2)

=[l(T1，T2)]α·[c(T1，T2)]β·[s(T1，T2)]γ

(1)

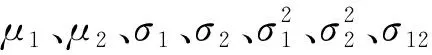
采用滑动窗口逐行计算双时相影像间的光谱特征结构相似度，能充分利用像元的邻域特征并减弱配准误差带来的影响。以子对象中所有像元的结构相似度均值作为该子对象的变化强度值构建变化强度图。

2.3 多尺度变化强度模糊融合

本文引入模糊集理论以解决各尺度下同一空间位置像元变化情况判别结果冲突问题。采用常见的S型隶属度函数[9]来计算隶属度值，该函数为偏大型函数，在影像模糊分割处理时有较好的稳定性。假设在分割尺度为k时某像元的变化强度值为Vk(i，j)，则该像元属于未变化类别的隶属度值为Mu(Vk(i，j))，同时属于变化类别的隶属度值为Mc(Vk(i，j))。隶属度值间的关系为：Mu(Vk(i，j))=1-Mc(Vk(i，j))，且0≤Mc(Vk(i，j))≤1，0≤Mu(Vk(i，j))≤1。显然，Mc(Vk(i，j))值越接近1，则变化强度值Vk(i，j)属于变化类别的可能性就越大；反之，Vk(i，j)属于未变化类别的可能性就越大[10]。公式(2)给出了变化强度值Vk(i，j)属于变化类别的隶属度值计算式。

(2)

上式中，将各分析尺度下的变化强度图通过Otsu法获得的分割阈值作为ck的取值，因大多数情况下影像中变化地物占比较小，因而令ak=0.8ck，bk=(ak+ck)/2且Mc(bk)=0.5。取3个分析尺度时，多尺度下的模糊隶属度关系矩阵为：

(3)

采用文献[11]的自适应融合策略，对3个尺度下的变化强度图进行融合。利用各尺度下变化强度图的灰度信息熵来计算某一尺度下的变化强度权值。基本原理为各灰度级的概率值p(j)相等时，灰度图像的熵值最大。而变化强度图上仅有变化和未变化两种类别，因此，在变化强度图上熵值越小越容易区分是否发生变化，因而熵值越小变化强度的权值越大。若3个尺度下对应的变化强度图的熵值分别为H1、H2、H3。则每个尺度变化强度图的自适应权值Wi可按下式计算：

(4)

式中Hi为各尺度下变化强度图的熵。设某一影像有N个灰度级，且灰度级n(0≤n≤N)出现的概率为p(n)，则该图像的信息熵Hi可按下式计算：

(5)

则多尺度变化检测模糊加权融合结果为：

M(i，j)=(Mc(i，j)，Mu(i，j))=WiR(i，j)

(6)

其中Mc(i，j)和Mu(i，j)为多尺度变化信息融合后，像元(i，j)属于变化像元和未变化像元的加权隶属度值。像元(i，j)是否为变化的多尺度融合结果，按如下规则判定：Mc(i，j)>Mu(i，j)，则像元(i，j)为变化像元，反之为未变化像元。

3 实验

3.1 数据预处理

选取了西安市城区某地的谷歌地图影像和天地图影像进行实验(如图2所示)。所选的影像数据为利用LSV(Loca Space Viewer)软件下载获得。两期影像分别拍摄于2016年和2017年，其中时相1为天地图影像，时相2为谷歌影像。前后两期影像均为RGB三波段彩色影像，拍摄季节都是夏季，无云覆盖且成像清晰，亮度基本一致，空间分辨率均为 0.6 m，可满足城市变化检测实验的要求。

图2 预处理后影像

3.2 最佳分割尺度分析

利用易康软件的多尺度分割工具对两时相影像进行分割，并结合ESP2插件对影像中主要变化地物植被的最佳分割尺度进行分析，获得各影像的最佳分割尺度。城市地物复杂多样，并不存在适合所有地物的最佳分割尺度。即使是单一类别地物也不存在唯一的最佳分割尺度(例如本文实验中的主要变化地物植被)，因此需要采用一系列最佳分割尺度组合，才能够达到对某类地物合理刻画。为了便于分析，本文将一系列最佳分割尺度进行简化，保留大、中、小3种尺度。

基于本文实验影像进行多次分割实验，结果显示最小分割尺度选择60，形状因子0.1，紧致度0.5时分割结果的形状与实际地物轮廓较为吻合，即最佳分割尺度。以此为基础进一步分析得到一系列的最佳分割尺度。

3.3 参数设置

双时相影像的结构相似度计算中相关参数设置如下：α=β=γ=1，C1=C2=C3=0.001。各时相的多尺度分割采用易康软件的分割结果，子对象生成及后续实验均采用Matlab2017进行仿真实验。

4 结果与讨论

4.1 多尺度分割与子对象生成结果

利用ESP2工具进行最佳分割尺度估算，获得各影像的一系列最佳分割尺度。对每一幅影像在多个最佳分割尺度中，保留大、中、小3个尺度进行进一步分析。保留的最佳分割尺度如表1所示。

各影像植被的最优分割尺度 表1

利用表1中所列最佳分割尺度，分别对两时相影像进行多尺度分割，各尺度分割结果及子对象生成结果如图3所示。

从分割结果来看，大、中、小3种尺度下，绿地与非绿地图斑边界都分割得较好，混合图斑情况较少。不同尺度下，仅在绿地内部出现亚类区分边界，比如将草地和林地划分为同一图斑或分为不同图斑。将时相1与时相2的分割结果进行叠加，生成子对象并以RGB彩图形式显示如图3(c)、(f)、(i)所示。图中蓝色图斑即为有明显变化的新生成子对象。

图3 多尺度分割及子对象生成结果

4.2 多尺度变化信息融合

在3个尺度下分别计算双时相影像的结构相似度，得到不同尺度下的变化强度图，再将变化强度进行模糊化处理，最后进行多尺度变化信息加权融合，得到最终结果。各尺度下经模糊化处理后的变化强度图如图4(a)～(c)所示。图4(d)为多尺度变化信息模糊加权融合结果。

从多尺度变化信息图(图4)及多尺度变化信息融合检测精度(表2)可以看到，分割尺度越小检测到的细碎图斑就越多，误检率也越高。随着尺度的增大噪点进一步减少，误检率也逐步降低。融合图像在权值的影响下向着检测目标的方向调整，总体精度、Kappa系数、虚警率等指标与未进行多尺度信息融合前相比都得到了一定程度的提高。

图4 多尺度变化信息融合

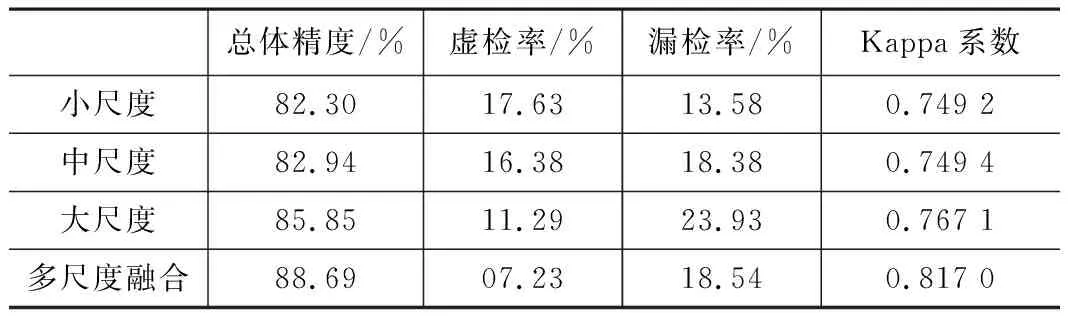
多尺度变化信息融合检测精度 表2

5 结 论

本文针对面向对象的变化检测中最优分割尺度难以确定问题，提出了多尺度分析的变化检测方法。该方法是对常规面向对象变化检测方法的一种改进，它在一定程度上弥补了单一分割尺度变化检测的不足，对面向对象的变化检测具有一定的普适性。

在西安市2016年天地图影像和2017年谷歌地图影像组成的影像对上进行变化检测实验。分别采用大、中、小3种分割尺度进行变化检测，并进行多尺度融合变化检测，对检测结果进行比较，实验结果表明多尺度融合变化检测比单一尺度变化检测精度有明显的提升。