基于均衡关系模型的因果方向推理
郭子诚
(福建师范大学计算机与网络空间安全学院 福建 福州 350117)
0 引言
因果推理正在成为机器学习中的热门主题[1],可以帮助人们捕捉到事物间所蕴含的规律,被广泛应用于金融[2]、医学[3]、气象[4]等领域。仅依据观测数据发现变量间的因果关系是因果发现方法所要解决的重点问题之一[5]。近年来研究者们从因果作用机制引发的数据分布特性等角度[6],提出了多种表示变量间因果关系的因果函数模型,其目的在于描述自变量的变化如何影响因变量的变化[7]。这类因果发现算法往往基于结构方程模型(SEM)[8],即将观察变量为节点的有向图表示成一组结构方程, 从而表示模型的因果结构。该类方法主要围绕有向无环图来建立因果模型,而分析双变量情况下变量间的因果关系是更加基础的研究。
Patrick等人[1]提出了一种基于回归误差比较的因果推理的分析方法(RECI),在如下假设下证明了因果方向上的拟合误差较小:假设关系模型、条件噪声分布、原因变量分布之间相互独立,假设两个变量的样本容量相等且变量间的因果关系接近确定性。其方法的主要思想是:首先,分别以关系模型Y=f(x)和X=g(y)在X→Y方向和Y→X方向上拟合数据集;然后,计算出两个方向上关系模型的均方误差MSEX→Y和MSEY→X;最后,比较均方误差MSEX→Y和MSEY→X的大小,推理均方误差较小值所在的方向为因果方向。
RECI方法使用了逻辑函数、单项函数、多项式函数、支持向量机、神经网络共5种关系模型进行多次实验,实验结果显示选择不同的关系模型会得到不同的结果。
总之,不同数据集具有不同的特点,如果关系模型选择不合适则匹配数据集的效果差,甚至可能推理出错误的因果关系。针对如何设计适合的关系模型来匹配两个变量间关系的问题,本文提出一种基于均衡关系模型的因果方向推理方法,设计基于非线性多项式函数的均衡关系模型和推理变量间因果关系的方法,解决了关系模型与数据集不匹配可能带来的推理错误问题。
1 背景知识
1.1 基于回归误差的因果推理方法
文献[1]基于误差不对称定理,提出一种基于回归误差比较的因果推理的分析方法,实现了仅依据观测数据推理变量间的因果关系。该误差不对称定理的条件和假设如下[1]:
设原因变量C、结果变量E,关系模型φ(C)=M[E|C],其中M[E|C]表示给定原因C时结果E的条件期望,N=E-φ(C)为噪声,α控制噪声的大小,Eα=φ(C)+αN为结果变量族。
假设1:C、E均在区间[0,1]内紧凑分布,二者间的因果关系接近确定性。
假设2:φ是二阶可微的可逆函数。
假设3:给定原因变量C,噪声变量N的条件方差的期望M[Var[N|C]]=1。
假设4:因果关系函数φ、条件噪声分布Var[N|C]、原因分布pC之间是独立的。
若上述假设成立,则以下极限始终成立
(1)
其中,只有当φ为线性函数时等号成立。
RECI算法的主要步骤为:首先,分别在两个可能的方向上用同种关系模型进行回归拟合Y=f(x)和X=g(y);然后,计算出两个可能的方向上回归模型的均方误差值MSEX→Y和MSEY→X;最后,比较两个均方误差值的大小,基于误差不对称定理推理均方误差值较小的方向为因果方向。
从上述可知,对于二变量的情况RECI算法在两个不同的方向上使用回归模型拟合数据,比较两个方向上的均方误差的大小,推理均方误差值较小的方向为因果方向;此方法设计简单,易于实现。
1.2 贝叶斯信息准则
如何从候选模型中选择出拟合样本数据集的模型,是经典的模型选择问题。训练样本的似然会随着模型参数(维数)的增加而增加,尤其在维数过大而训练样本相对较少的情况下,会造成“维度灾难”[9]。当我们以模型拟合数据的误差最小为目标时,倾向于选择具有更多参数的复杂模型,造成过拟合问题。
贝叶斯信息准则(BIC)能够从备选模型中寻找一个具有良好预测能力的精简模型[10],其主要思想是在模型的复杂程度与模型拟合数据集的精度之间找到最佳平衡。BIC定义为
BIC=m×ln(n)-2×ln(L)
(2)
其中,m表示模型中待求解参数的个数,n表示数据集的样本数量,L表示模型的似然函数,m×ln(n)是对模型复杂度的惩罚项[11]。
2 基于均衡关系模型的因果方向推理方法
RECI方法未设计何种关系模型用于因果推理,若关系模型选择不当可能不匹配数据集,可能推理出错误的因果关系,本节设计基于均衡关系模型的因果方向推理方法,在建立关系模型阶段,采用非线性多项式函数族作为备选关系模型,利用双向贝叶斯信息建立合适的关系模型来推理变量间的因果关系。
2.1 方法设计
由于多项式函数相对简单、较为灵活,且任何类型的函数都可以通过多项式逼近,因此多项式函数有着广泛的应用[12]。新方法采用非线性多项式函数族[13]作为原因变量C与结果变量E之间的备选关系模型,其性能受到模型阶数k的影响。在利用模型拟合数据集时,不同模型拟合数据集的效果是有差别的。因此,对于多项式函数族,阶数k如果选择过小,可能会导致模型欠拟合;但模型的阶数k如果选择过大,可能会致使模型过拟合,从而导致泛化能力的下降和模型复杂度的升高[14]。
为了提高模型对数据的拟合程度,同时也避免过拟合问题,可以采用贝叶斯信息准则使模型复杂度和模型性能达到最佳平衡。对于因果方向推理任务,借鉴贝叶斯信息准则设计均衡模型,并提出如下定理给出选用关系模型的规则,以解决现有的RECI方法没有关系模型选用规则的不足。
定义1(均衡模型):设使用多项式关系模型Model拟合数据集D的阶数在[ka,kb]范围,ka为显著欠拟合阶数,kb为显著过拟合阶数;利用贝叶斯信息准则选出的如下K*∈[ka,kb]的多项式为均衡模型,且均衡模型既不欠拟合数据,也不过拟合数据。
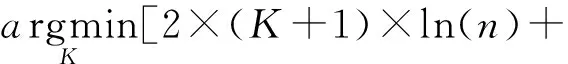
n×ln(SSE(K)X→Y+SSE(KY→X)]
(3)
其中,n表示数据集的大小,SSE(K)X→Y=∑(Y-f(x))2表示X→Y方向的误差平方和;SSE(K)Y→X=∑(X-f(y))2表示Y→X方向的误差平方和。
定理1(均衡模型推理因果方向):设使用多项式关系模型Model拟合数据集D={(xi,yi)}的阶数在[ka,kb]范围,2个不同数据集的因果方向不同。对于以回归误差小的方向判别为因果方向的RECI准则,若保证RECI准则的有效性,关系模型应选用相同阶数多项式且是均衡模型。
证明:
采用反证法,否定结论得到2个假设,即假设1:选用非相同阶数多项式;假设2:选用非均衡模型。
设数据集D={(xi,yi)}经过标准化处理后,X对应的数据和Y对应的数据的分布相差不大。设阶数从ka增长到kb,多项式关系模型拟合数据的能力逐步增强,其拟合残差逐步减小。
设正方向X→Y的关系模型为f(x),模型阶数为k1,残差为e1=Y-f(x),回归方程为
(4)
设反方向Y→X的关系模型为g(y),模型阶数为k2,残差为e2=X-g(y),回归方程为
(5)
按照假设1选用多项式时,正方向和反方向所采用的模型阶数有2种情况。
(1)当k1 (6) 对比公式(4)与公式(6)可知,相比于正方向,反方向的模型g(y)多出(k2-k1)项表达式,拟合数据的能力更强,拟合残差更小。 对于分布相差不大的X数据和Y数据,对模型f减小k1,对模型g增大k2,会出现e2一定程度小于e1,则当k1→ka,k2→kb时有如下关系式(其中C>0) e2+C (7) 这使得对于因果方向不同的2个不同数据集,e2 因此当k1 (2)当k1>k2时,式(4)可以表示为 (8) 对比公式(5)与公式(8)可知,相比于反方向,正方向的模型f(x)多出(k1-k2)项表达式,拟合数据的能力更强,拟合残差更小。 对于分布相差不大的X数据和Y数据,对模型f增大k1,对模型g减小k2,会出现e1一定程度小于e2,则当k1→kb,k2→ka时有如下关系式(其中C>0) e2>e1+C (9) 这使得对于因果方向不同的2个不同数据集,e2>e1总是成立,则依据回归误差小的方向判别为因果方向的准则,因果方向必为X→Y;这与已知条件(2个不同数据集的因果方向不同)矛盾。 因此当k1>k2时,不能保证RECI准则的有效性。 由以上推理结论可知,假设1不成立。 下面讨论假设2的情况。前文已证明非相同阶数多项式不可行,于是对于k1=k2=k时的非均衡模型,或者是欠拟合关系模型,或者是过拟合关系模型展开讨论。 当k1=k2=k时,式(4)、(5)可以表示为 (10) (11) 对比公式(10)与公式(11)可知,正反方向的模型f(x)与g(y)表达式结构相同,拟合数据的能力也相同。 假设kb为模型f和模型g完美过拟合数据时的模型阶数,此时模型拟合的回归误差为0;当k→kb,模型f和模型g都过拟合,倾向于非常好地拟合数据,导致e2近似等于e1;此时,或者RECI准则失效,或者可能的微小计算误差就带来变量间因果关系的改变。 假设ka为模型f和模型g严重欠拟合数据时的模型阶数,此时模型严重偏离数据,其拟合误差极大。当k→ka,模型f和模型g都严重欠拟合,模型倾向于严重偏离数据,导致出现异常的e2与e1非常大。此时,2个严重偏离数据的模型之间的对比,2个异常的大误差比大小,没有任何意义,RECI准则失效。 由以上推理结论可知,假设2不成立。 以上定理说明,对于RECI准则,关系模型选用任意阶数多项式时不能保证判别结果的正确性,而选用相同阶数多项式的均衡模型能保证判别结果的正确性。均衡模型推理因果方向定理给出的本文方法,综合考虑两个方向上关系模型的性能与复杂度,既能使得模型的性能与复杂度达到均衡,又能保证因果方向判别结果的正确性。 在关系模型建立阶段,本文设计无1次阶自变量的K*阶多项式(公式12)来建立关系模型。 (12) 这种设计只使用了自变量的2次阶及以上,相比于全阶次的经典多项式,其优势是更专注于变量间的非线性关系。考虑1次阶自变量的线性关系模型适合数据集的情况,依据误差不对称定理的条件,RECI方法在k=1时无法推理因果方向。故此,需要寻找替代方法。由于基于信息熵的IGCI方法[15]利用原因变量的分布和“因-果”函数机制的独立性来判断变量间的因果关系[6],避开了关系模型问题,可以作为替代方法。在本文方法选择1阶关系模型时选用IGCI方法判别因果方向。 基于均衡关系模型的因果方向推理方法(BM)的步骤如下。 假设数据集{X,Y}的样本规模为n,其中X={xi},Y={yi},i=1,2,…,n。X→Y表示X是Y的原因,其关系模型记为Y=f(x);Y→X表示Y是X的原因,其关系模型记为X=g(y)。假设关系模型f和g的形式采用相同的K阶多项式回归模型。 步骤1:数据预处理。对每个变量的数据进行预处理,规范化到[0,1]范围。 步骤2:建立关系模型。通过定理1寻求最佳阶数K*,当K*=1时利用IGCI方法进行因果方向判别;当K*>1时,则将无1次阶自变量的K*阶多项式作为关系模型。 步骤3:求解关系模型。针对X→Y方向,使用数据集{xi,yi}求解模型Y=f(x);针对Y→X方向,使用数据集{yi,xi}求解模型X=g(y)。 步骤5:因果方向判别。推理变量X、Y间均方误差较小的方向为因果方向。 本节对模拟数据和真实数据进行实验检验本文方法的性能,并与RECI等多种方法进行对比实验。 双变量(X与Y)模拟数据集来自文献[16],共有3种类型:无混杂因素的场景SIM,无混杂因素且X近似服从高斯分布的场景SIM-G,与SIM类似但带有混杂因素的场景SIM-c,其中,每种类型均由100个样本规模为1000的数据集组成,更多细节请见文献[16]的附录C。 在实验前,统一将数据规范化到[0,1]范围;备选模型阶数m的取值范围为1~12。由于文献[1]中未提供具体代码,所以此次实验中RECI方法的代码来自于文献[16]。实验中,IGCI模型的值用r表示,若r大于0则推理因果方向为X->Y;否则为Y->X。 数据集来自SIM:pair17。由文献[1]可知,当多项式阶数k=3时RECI方法在SIM数据集上表现最佳。因此,选择k=3的固定阶次多项式作为关系模型,利用RECI方法判别SIM数据集:pair17的因果方向;同时,再使用本文方法与之进行对比。实验结果如表1和图1所示。 表1 本文方法与RECI方法在模拟数据集上的实验结果 由图1可知,RECI固定阶次的模型未能匹配数据集的分布规律;而本文方法拟合线的走势接近于样本点的分布,样本点沿着拟合曲线的方差较小。 图1 本文方法与RECI方法在模拟数据集上的拟合图像 CEP数据集Fine Aggregate-Compressive Strength来自UCI Machine Learning Repository由Mooij等人收集[16],该数据集记录了混凝土中细骨料的含量(X)与混凝土的抗压强度(Y),混凝土中细骨料的含量是其抗压强度的原因。由文献[1]可知,当多项式阶数k=3时RECI方法在CEP数据集上表现最佳。因此,选择k=3的固定阶次多项式作为关系模型,利用RECI方法判别Fine Aggregate-Compressive Strength数据集的因果方向;同时,再使用本文方法与之进行对比。实验结果如图2、表2所示。 图2 RECI方法在Fine Aggregate-Compressive Strength数据集上的拟合图像 表2 本文方法与RECI方法在Fine Aggregate-Compressive Strength数据集上的实验结果 图2显示,Fine Aggregate-Compressive Strength数据集的两随机变量间具有非线性关系,其分布较为复杂。难以表示样本。而本文方法阶次K*=1,使用IGCI进行因果方向判别,有效避免了模型无法匹配样本的问题。 在本节实验中,本文方法将与RECI、ANM、IGCI、SLOPE、LiNGAM、CURE等方法进行对比,所有对比方法的实验结果抄录自文献[1]。 在对比分析时,我们使用准确率作为方法性能的评估指标: (13) 其中,P表示数据集个数,δj表示第j个数据集的实验结果,δj={0,1}。其中,δj=1表示因果方向推理正确,δj=0则表示推理错误。wj表示第j个数据集的权重。由于真实数据集中一些数据集较为相似而无法作为一个独立的例子,所以将获得较低的权重,详细参考文献[16]。 真实数据集CEP采用由Mooji等人提供的100个具有给定因果关系的数据集[16]。这些数据集包括各种不同的情况,例如依赖时间和独立的物理过程、社会学和人口研究或生物和医学观察的数据[1]。全部真实数据集的实验结果如表3所示。 由表3可知,RECI方法性能较低的原因是:模型不符合样本的规律,导致模型具有较差的拟合能力。实验结果显示,BM方法表现最佳。 表3 各方法在Benchmark数据集上的准确率 本文基于均衡关系模型的因果方向推理方法考虑了关系模型对因果方向推理的影响,设计基于非线性多项式的均衡关系模型,实现变量间的因果方向推理。新方法可以避免由不合适关系模型导致因果方向推理的错误。关系模型影响算法的性能,针对其他回归方法如何设计关系模型值得进一步研究。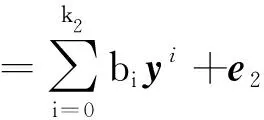
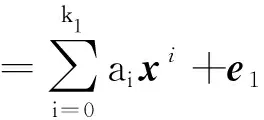
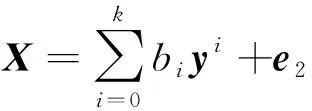
2.2 方法步骤
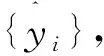
3 实验及结果分析
3.1 实例分析实验
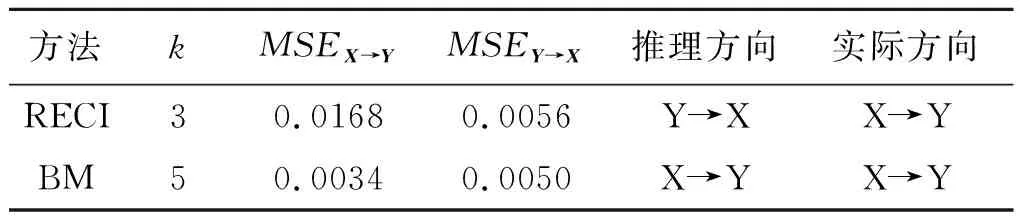



3.2 在Benchmark数据集上对比实验

4 结束语

