基于共生生物算法的装配式建筑塔吊布局优化研究
汪和平, 袁睿晗
(安徽工业大学管理科学与工程学院 安徽 马鞍山 243002)
0 引言
塔吊作为装配式建筑施工中核心施工机械直接影响施工效率和施工机械成本。在以往文献中对装配式建筑塔吊的布局优化研究较少,同时将传统建筑塔吊的布局方案使用在装配式建筑施工中,其所展现出的结果并不令人满意。首先传统塔吊布局只需要满足需求点最大吊装重量即可,忽视了需求点其吊装材料的重量,而装配式建筑中塔吊吊装的主要是预制构件,预制构件不仅比传统建筑的材料重量更大,不同种类预制构件之间的重量相差也较大,只考虑需求点最大吊装重量可能导致塔吊位置并非是最优的;其次就是在传统建筑中吊装材料到需求点后卸载时间较短,而在装配式建筑中塔吊除了参与预制构件运送时间还需要参与预制构件安装时间,增加了塔吊的使用时间和频率;最后相较于传统施工塔吊数量,在装配式建筑施工中塔吊的数量更多密集度更大,塔吊之间可能会存在多个任务重叠区域,在高效的前提下,对塔吊合理布局对施工安全具有重大影响。
一直以来国内外学者对塔吊的位置布局的研究层出不穷,大多数学者都是以塔吊施工的效率和成本做为主要的目标函数进行研究,但研究侧重的因素各不相同。针对塔吊的成本和效率,Olomolaiye[1]在1999年根据塔吊的运行提出了一组塔吊优化模型,在其中分为3个子模型分别对塔吊的效率、工作量、冲突可能性进行分析;塔吊位置布局优化中任务重叠区域碰撞问题是研究的热点之一,Younes[2]基于一种代理仿真模型,对塔吊运行成本和时间进行模拟仿真,巧妙解决了多塔吊之间相互冲撞的问题;Dirk[3]以塔吊成本为目标函数,侧重于对塔吊活动冲突的影响因素,开发了4种混合整数规划模型对塔吊的选型和位置布局进行优化;Monghasemi[4]基于博弈和优化论的方法,考虑减少重叠区域任务等待时间来提高塔吊布局中的效率;Wu[5]将塔吊本身的数量、类型、位置、使用期限和高度等级组成的相互作用的规划对象纳入数学模型,并且重点考虑重叠区域内的任务等待时间;供需点的供需关系也是塔吊研究热点之一,Zhang[6]考虑施工现场的动态交互约束开发了基于供需关系的数学模型,并基于粒子群优化对其进行求解; Riga[7]基于混合整数规划提出了一个数学模型,用于计算塔式起重机和供应区域的成本最优位置;高层项目及城市狭窄施工地带对塔吊布局的影响也是研究热点,Hasan[8]基于起重机效率、碳足迹影响,模拟了高层建筑施工项目的起重机选择方法;对于塔吊小车的运动,众多学者都是采用小车匀速运动的观点,但Allan[9]认为这种观点在塔吊运动中会对塔吊的布局产生影响,他提出了一个数学模型来生成工作时间优化的起重机操作,将吊车看作为从0开始的加速运动并对塔吊布局进行分析;施工现场的量化,刘猛[10]将塔吊施工现场进行网格化,并基于混合整数规划模型对塔吊的位置布局进行优化;李文杰[11]针对装配式建筑施工工序进行塔吊布局的优化,并使用遗传算法进行求解。
在塔吊布局优化模型中,精确和启发式方法都已经被用于解决塔吊布局问题。Prayogo[12]开发了一种本地算子混合共生生物搜索算法对施工现场和塔吊的优化布局进行求解;Alkriz[13]开发了一种基于遗传算法的优化系统和决策支持工具,以确定起重机和建筑工地设施的最佳位置;Wang[14]开发了一种结合建筑信息模型和萤火虫算法的集成方法,以自动生成最佳塔式起重机布局计划;Lien[15]将粒子蜜蜂算法应用于塔吊布局优化问题;Abdelmegid[16]开发一种优化模型来解决建筑工地塔式起重机定位问题,目标是最小化总运输时间,并且使用遗传算法来解决这个问题。
在以往的文献中针对传统建筑的塔吊布局优化研究较多,在传统建筑施工中由于运输材料重量、类型、次数的不确定性,使得众多学者对塔吊位置布局的研究都是以塔吊为中心,根据塔吊的运行、冲突等因素对塔吊位置布局进行分析。但是在装配式建筑中,预制构件的总数量、预制构件的分布、重量等在施工前都有明确的规定,并且对其他建筑材料、建筑垃圾等吊装较少。因此文章基于装配式建筑的特点即预制构件的明确化,以预制构件的分布为基础,并结合现有的研究理论和装配式建筑施工现场实际考察情况,建立塔吊的布局优化模型,综合考虑塔吊成本、吊装效率、塔吊覆盖率的多目标优化,列举多个如重叠区域任务分配、任务等待等重要约束,并基于改进的多目标共生生物算法(IM-MOSOS)对模型进行求解。
1 问题分析
1.1 问题描述
由于吊装材料的不同,装配式建筑塔吊的位置布局和传统塔吊位置布局会有较大的差异,因此对装配式建筑塔吊位置布局的优化需要以预制构件的种类、重量、分布为中心结合安全、供需、重叠区任务等其他约束综合研究在装配式建筑中塔吊的布局优化。装配式建筑塔吊位置的布局优化主要分为3个部分:(1)对塔吊型号进行选择。由于吊装预制构件装配式建筑所需的塔吊吊装能力更强,塔吊的型号选择是必不可少的;(2)对塔吊的运行进行分析。塔吊的运行主要分为3个部分:吊臂运动、小车沿吊臂运动、小车垂直运动。(3)对选择的塔吊进行布局优化。对确定型号的塔吊进行布局优化,此时要考虑到塔吊施工效率、成本、覆盖率、塔吊施工等待时间等多个限制条件,以保证能适应装配式建筑施工。
此外还需要对塔吊的运行轨迹进行分析,塔吊位置优化中包含多个约束条件及影响因素,如多塔吊重叠区域碰撞、重叠区域任务分配、等待时间划定、塔吊安全距离等,这些约束会影响塔吊的布局优化,需要对这些约束进行优化处理否则可能达不到预期的目的。
1.2 施工场地数据量化
文章将施工场地进行网格化并且建立坐标系,每个网格都赋予其内容含义例如需求点(5.15.12)其中包含3块预制柱、4块预制墙等内容,并将数据输入至Matlab中。文章选取10种装配式建筑中常用的塔吊型号进行塔吊吊重及成本分析,塔吊吊臂所能吊动的重量是随着吊臂的长度的增加而减少,并且其吊重趋势相同,同时调动成本随着吊臂长度而增加,图1显示塔吊吊臂所能吊重的重量和小车幅度的关系,图2显示了塔吊塔吊吊幅和成本关系。

图1 吊臂吊重与小车幅度关系

图2 塔吊吊辐和成本关系
1.3 塔吊运行分析
塔吊运行分为3方面:(1)塔吊吊臂的切向运行;(2)塔吊吊钩沿吊臂方向的径向运动;(3)吊钩的垂直运动。
首先根据公式(1)至(4)计算出塔吊、供应点、需求点三者两两之间的直线距离。
(1)
(2)
(3)
(4)
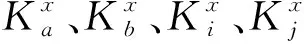
其次根据公式(5)计算吊钩垂直运行的时间,根据公式(6)计算出塔吊吊臂的径向切线运动时间,根据公式(7)计算出塔吊沿吊臂运行的时间。
Tvi=|zS-zD|/Vhi
(5)
Tai=|ρ(Dj,Ka)-ρ(Si,Ka)|/Vai
(6)
0≤arccos(·)≤π
(7)
式中,Tai表示吊臂切线运动的时间;Vai表示吊臂径向运动的速度;Tvi表示吊钩垂直运动的时间;Vhi表示垂直运行的速度;ZS、ZD表示供应点和需求点的高度;Tωi表示吊钩沿吊臂方向运动的时间;Vi表示吊钩沿吊臂方向运行的速度。
再次考虑塔吊司机因预制构件不同或者其他原因所导致的操作水平差异,而影响塔吊运行时间,引入系数α来衡量这种操作差异。α的取值在0~1之间,数值越大其操作水平就越差,切向与径向运动越离散,水平运动的时间更长。
Thi=max(Tai,Twi)+α×min(Tai,Twi)
(8)
式中,Thi表示塔吊水平运动的总时间,在塔吊吊钩运动时间和塔吊吊臂切向运动时间之间取最大值,再加上因预制构件不同或者其他原因所导致的操作水平差异而影响的时间。
最后将塔吊水平与竖直运动与水平运动加和,并总和装载时间与卸载时间,构成单台塔吊一次运输预制构件所需要的全部时间。为平衡竖直运动和垂直运动之间的连贯性,引入系数β,β取值在0~1之间,当数值越大时,其离散性越大,塔吊总的运行时间就会越长。
Ti=max(Thi,Tvi)+β×min(Thi,Tvi)
(9)
Tr=Tloading+Tunloading+Ti
(10)
1.4 条件假设
为方便计算,假设以下条件成立:(1)施工场地除供应点和需求点外,其他位置都可以安装塔吊;(2)施工现场的土壤质量允许安装塔吊;(3)施工时只计算预制构件吊装,忽略其他材料的吊装。
2 模型建立
2.1 目标函数
2.1.1 塔吊吊装成本最小
(11)
K表示塔吊数量;L表示塔吊型号;M表示预制构件种类;N表示预制构件单位时间运行成本;Qk,l表示l型号k塔吊单位时间租赁成本;Tg租赁总时间;Pm,n表示m构件成本为n;Tm表示塔吊吊m预制构件的运行时间。
塔吊成本受塔吊型号和吊装的预制构件所约束,选择的塔吊型号不同每个月的租金不同;预制构件共有M种,吊装成本随预制构件本身重量和所处塔吊吊臂的位置不同而改变。预制构件m在不同长度吊臂处的成本
Pm,n=ωm·Cdt
(12)
Cdt=b+r/5*Cx
(13)
Cdt表示塔吊在某处的单位小时吊装成本,b表示吊装基础成本,Cx表示不同吊臂处的成本增长系数。
2.1.2 塔吊吊装效率最大
MinT=Tr+Td
(14)
T为运输预制构件时间和塔吊任务等待时间总和;Td为塔吊任务等待时间。
2.2 约束条件
2.2.1 安全距离约束
影响塔吊布局的安全因素主要包含:(1)塔吊与塔吊之间的安全距离,从一台塔吊吊臂头到另一台塔吊吊尾至少2 m距离;(2)塔吊与建筑物、堆场之间的安全距离,塔吊到建筑或堆场之间要至少存在3 m的安全距离,这3 m不仅仅是安全距离也是塔吊吊臂最小使用距离,如果小于3 m塔吊可能无法对建筑物、堆场进行施工;(3)塔吊与塔吊重叠区域的碰撞,为提高施工效率在施工现场很可能出现多台塔吊对某一区域进行施工的情况,同时施工就可能发生碰撞问题,施工方对塔吊施工任务进行排序可以避免发生碰撞。
公式(15)、(16) 实现一台塔吊k吊臂与任意一台塔吊k’安全距离为Δ。公式(17)、(18)限制任意一台塔吊k距离建筑最小安全距离为θ。
2-αe,k,l-αe′,k′,l′≥1-φ(e,k,l),(e′,k′,l′),∀e,e′∈E,∀k,k′∈K,∀l,l′∈L
(15)
φ(e,k,l),(e′,k′,l)′(Dk,k′-max(Rl,Rl′)-Δ)≥0,
∀e,e′∈E,∀k,k′∈K,∀l,l′∈L
(16)
(17)
ηk,d≥αe,k,l,∀k∈K,∀d∈D,∀e∈E,∀l∈L
(18)
αe,k,l为0,1变量表示l型号k塔吊存在单元格e内;φ(e,k,l),(e’,k’,l’)表示n和n’两种型号塔吊k和k’分别位于单元格e和e’内;Rl和Rl’表示塔吊k和k’的吊臂长度;Dk,k’表示位于单元格e和e’之间的距离;Δ表示塔吊k的吊臂与塔吊k’最小安全距离(一般为2 m);ηk,d为0~1变量,表示塔吊k和需求点d是否满足最小安全距离约束;Dk,d表示需求点d到塔吊k的安全距离;θ表示最小安全距离(一般为3 m)。
2.2.2 预制构件供需约束
考虑预制构件供需约束时,首先要考虑的就是塔吊吊装能力问题。装配式建筑预制构件普遍较重,有时塔吊吊臂可以覆盖某位置,但由于塔吊吊装能力是随着吊臂增长而减少的,吊臂过长也会出现吊装能力不足而无法吊装的情况,因此要结合预制构件重量和塔吊吊臂的吊装能力综合判断塔吊能否对供应点需求点进行吊装。其次则是要考虑预制构件的供需要求,与以往固定堆场的情况不同,现在的装配式建筑施工时为避免出现二次搬运导致预制构件损坏情况,部分施工方要求预制构件运输到施工现场后直接进行吊装而不进行搬运,这就会使只要有预制构件运输那必定会满足塔吊的吊装需求而无需对预制构件种类等进行约束。最后则是要求一台塔吊一次性只能运输一块预制构件,保证任务独立性。
式(19)表示表示l型号塔吊k在需求点d处的吊装能力;式(20)表示l型号塔吊k能否在需求点d处满足其吊装需求;式(21)表示l型号塔吊k能否同时满足供应点s和需求点d的吊装能力需求。同时要保证每个需求点由一台塔吊来供应,一个供应点可以对应多个需求点,但一个需求点只由一个供应点供应。公式(22)和(23)表示每个预制构件吊装任务只能由一台塔吊运送完成。
(19)
φd,k,l={1,Cd,k,l≥Wd0,Cd,k,l
(20)
(21)

(22)
2-εs,d,k,l-γs,d,m≥1-δs,d,k,m,l
(23)
Cd,k,l表示l型号塔吊k在需求点d处的最大起吊重力;Wd表示塔吊在工作范围内各需求点处的最大起吊重力;φd,k,l为0,1变量,表示型号l的塔吊k在需求点d上是否满足该处的最大起吊重量;φs,k,l为0,1变量,表示l型号塔吊k能否满足供应点s的吊重重量;εs,d,k,l为0~1变量,表示l型号塔吊k能否满足供应点s到需求点d的运送需求。δs,d,k,m,l表示l型号塔吊k可以将预制构件m从供应点s运送到需求点d上。γs,d,m表示供应点s能为需求点d提供预制构件m。
2.2.3 重叠区域任务分配及任务时间等待
非重叠区域塔吊只需要按照吊装顺序进行吊装即可,判断第i天需求点d的塔吊数量,若塔吊数量等于1,则将第j次的吊装任务分配到l型号塔吊k上,计算塔吊k第j次的吊装时间及安装时间计入到塔吊k的累计施工时间之中,等到安装完所有任务后计算塔吊k的总时间。
而在重叠区域塔吊吊装可能会受到多种因素影响,首先建筑施工时必然存在施工顺序例如先安装预制柱、预制墙之后才能安装预制梁等,由于存在施工顺序导致重叠区域可能会有多台塔吊同时施工,一般情况下对重叠区域的施工任务取就近原则。判断第i天需求点d的塔吊数量,若塔吊数量大于1,则判断是否只存在一台空闲塔吊k,若存在空闲塔吊k则直接将任务分配给空闲塔吊k,将时间计入塔吊k的累计施工时间之中;若不存在唯一空闲塔吊或者不存在空闲塔吊,则判断塔吊累计工作时长,将任务j分配给累计工作时长最小的塔吊k’,将时间计入塔吊k’的累计施工时间之中,等到安装完所有任务后计算塔吊k’的总时间。
公式(24)判断塔吊是否有重叠区域;公式(25)表示将需求点任务d分配给总任务时间最小的塔吊
(24)
(25)
χk为0~1变量,表示塔吊k’是否在与塔吊k的重叠区域内进行任务,若为1则将等待时间Td计入到塔吊k的累计时间之中,否则塔吊直接进行工作;dk表示需求点d是否被塔吊k所吊装。
2.2.4 塔吊覆盖率.
在对塔吊进行布置时要考虑塔吊能否对施工建筑全覆盖,在建筑施工时如果对施工建筑全覆盖虽然会增加施工效率但可能会增加施工成本。在传统中低层建筑中即使塔吊不对建筑全覆盖也可以通过小距离运输达到材料需求的要求,但是在装配式建筑中,由于吊装的都是大重量预制构件,如果塔吊无法对施工建筑达到全覆盖就需要使用汽车起重机对其进行辅助施工,这会增加施工成本,而高层建筑则必须让塔吊对建筑进行全覆盖,否则无法全面施工。
公式(26)保证塔吊对需求点的全覆盖。
(26)
Cov为塔吊对建筑的覆盖率,因需要对需求点全覆盖在实际案例中保证Cov=1;ξe为0~1变量,表示单元e被塔吊覆盖;E表示需求点单元格的总数量。
3 算法设计:共生生物搜索算法
3.1 共生生物搜索算法简述
Cheng等[17]于2014年提出了一种新的元启发式算法:共生生物搜索算法。这种算法是模拟自然界共同生活在同一生态系统内的各生物之间相互作用关系,在自然界中,生物之间存在互惠共生、偏利共生和寄生这3种关系。算法步骤如下:(1)互惠共生:互惠共生是双方都受益的阶段,比如蜜蜂传递花粉,花粉得到传播,蜜蜂得到食物。(2)偏利共生:偏利共生是一方受益但对另一方无损的阶段,比如地衣附着在树皮上获取水分空气等,但这并不影响树木的生长。(3)寄生:寄生阶段是一方获益而另一方有害(被淘汰),比如真菌寄生在蚂蚁身体内获取蚂蚁的养分获益,最终导致蚂蚁死亡。
共生生物搜索算法的稳定性好、操作性高、控制参数少,当然该算法也存在启发式算法的通病,诸如早熟、收敛慢、后期迟缓等问题。后续众多学者对算法进行改进,包括算法的初始解、寻优过程、全局探索能力等方面,使算法更为完善[18-21]。
3.2 改进共生生物搜索算法
文章在基于共生生物搜索算法的基础之上,对算法的寻优过程等方面进行了修改完善,后续为增加算法的全局探索能力,增加了经营选择和变异机制。
3.2.1 互惠共生阶段的改进
将互惠共生阶段的Xbest改成随机的Xt,并且Xt不等于Xi不等于Xj,方程为
Xinew=Xi+rand(0,1)*(Xt-Mutual_Vector*BF1)
(27)
Xjnew=Xj+rand(0,1)*(Xt-Mutual_Vector*BF2)
(28)
Xbest本为当前阶段最优解,为扩大初始搜索范围将其改为随机解Xt。rand(0,1)为随机数向量,Xi和Xj为生态系统中随机选取的。Mutual_Vector=(Xi+Xj)/2代表生物体Xi和Xj之间的关系特征。BF原本取值为1或者2,为了提升计算能力,此处固定BF取值为1,即令两方均受益满足互惠共生的目的。
3.2.2 偏利共生阶段的改进
在偏利共生阶段rand(-1,1),范围过于宽,使得其收敛速度变慢,尝试修改其为(0.4,1),在保证计算准确性的情况下,减少计算的成本。方程为
Xinew=Xi+rand(0.4,1)*(Xbest-Xj)
(29)
3.2.3 精英选择机制和变异
精英选择机制是将Xi和Xinew相结合形成一个2N的生态系统,从中选择N个最好的生物,形成一个新的生物系统。变异机制则是在精英选择机制前增加一个变异阶段,以增加算法的全局探索能力。
3.3 步骤简述
第一步初始化:初始化生态系统中有机体的数量种群规模,设置一个由p个有机体组成的生态系统,设置密度区间网格大小M,并且评估每个有机体的适应度值。
第二步快速非支配排序:基于帕累托理论对种群进行快速非支配排序构造出包非支配解集,该解集包含不同等级的解F={F1,F2,F3...Fn},随机选择一个解并将其做为最优解。
第三步互利共生:进入循环迭代的互利共生阶段,根据公式(27)、(28)进行迭代。
第四步偏利共生:进入偏利共生阶段根据公式(29)进行迭代。
第五步寄生:进入寄生阶段。
第六步变异阶段:进入变异阶段,根据已经设立好的概率判断是否发生变异文章采取互换法进行变异处理,也就是随机选择两位点进行变异。
第七步精英选择机制:结束一次迭代之后,进入精英选择机制,合并档案集和第一序列的支配解,对拥挤度进行排序,删除拥挤度最小的值,直到剩下40个,并且更新档案集。
第八步迭代次数判断:记录前沿解,判断是否达到最大迭代次数。
第九步结束。
4 案例分析
4.1 案例背景
以某地的一个预制件建筑项目为例,该项目是一个装配式住宅房项目,共分为3期,第一期小区内共14栋楼,每栋楼为4层,东西长为350 m,南北长为70 m。共O=26个大需求点,M=7个预制构件场地,大致分为N=5种预制构件。首先对施工现场进行量化,建立坐标系并进行施工场地网格化,找出对应的供应点和需求点并列出坐标。每个需求点所需要的预制构件种类和数量如表1所示,表2展示了施工方提供的塔吊型号选择及其相关参数。

表1 单个需求点的需求量
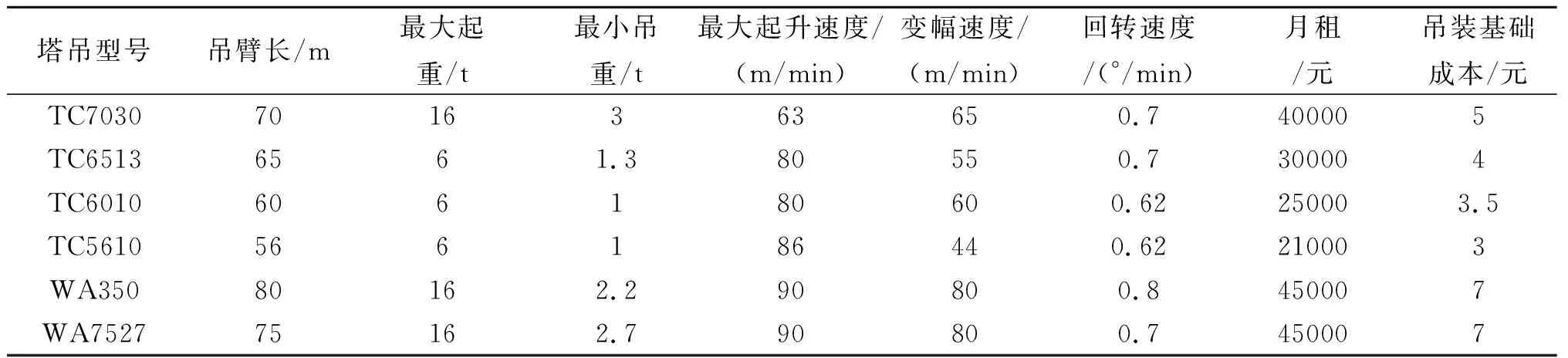
表2 塔吊型号及参数
4.2 计算结果与方案对比
使用Matlab2020a软件进行操作,分别使用IM-MOSOS算法、基础MOSOS算法和NSGA2算法对目标函数进行计算,种群大小取值为40,迭代次数为100。图3所示,IM-MOSOS算法收敛性更好所得解的范围更广质量更好更均匀,能为施工方提供更好的决策方案。

图3 3种算法最优解集对比
IM-MOSOS算法比其他算法所得的解更优(由于篇幅限制不再展示相应的解集),Pareto解集原则上并没有优劣之分,管理者可以根据实际情况进行取值,以作为最终方案。例如当需要尽快结束工期时可以选择第11个解,当需要尽可能减少成本时可以选择第1个解。在这里假设成本权重为0.4、时间权重为0.6,选取IM-MOSOS算法所得的第6个解进行展示如表3所示,并且与原方案进行对比如图4、图5所示。图中圆圈为塔吊吊臂所能覆盖范围,圆心为塔吊位置坐标。

表3 优化后方案

图4 塔吊原计划布局方案

图5 塔吊优化后布局方案
原计划中,塔吊总成本为200万元,总时间为500 h,最大吊装时间预计为150 h;经过优化后的塔吊总成本为189万元,总时间为462 h,最大吊装时间为73 h。经计算,虽然成本仅降低了3%,但总时间降低了6.24%,且最大吊装时间降低了50.06%。
由计算结果可以看出,优化后的方案增加了塔吊的固定成本,减少了塔吊吊装的变动成本,由此减少了塔吊的总成本提升了塔吊的吊装效率。因此,优化后的塔吊位置布局更有优势。无论对塔吊吊装速率还是塔吊成本控制,优化后的塔吊都有不同程度的降低,尤其是最大塔吊工作时间减少了50%。
5 结论
文章分析了装配式建筑塔吊的实际布局情况,提出了基于预制构件的种类、分布构建立塔吊位置优化模型并运用多目标共生生物搜索算法进行求解。文章首先考虑最小成本和单台塔吊最小时间模型并综合考虑多种因素影响,优化装配式建筑施工现场塔吊的位置布局,减少塔吊运行成本,提高塔吊施工效率;其次对共生生物算法改进,修改寻优公式、加入精英选择机制和寄生后的变异机制,增大算法搜索的范围。最后通过实例分析,验证了文章的模型与算法的在塔吊位置优化中可以起到明显的效果,有效提高塔吊效率,降低塔吊总成本,研究可以为装配式建筑施工中的塔吊优化提供一定的支撑。

