2021年高考数学上海卷第16题的多角度探究
安徽省肥东城关中学 (231600) 王东海
1 引言
2021 年高考数学上海卷第16题的题干简洁,没有繁冗的文字,和以往的选择题的最后一题比较,学生易想到使用构造函数和图像法,即它相对容易入题.但此题融入了众多数学思想与方法的考查,体现了对学生数学核心素养应用水平的较高要求,因而完成正确的求解并非易事.就笔者所进行的调查结果而言,本题的区分度好,不失为一道比较成功的选择压轴题.波利亚说:掌握数学就意味着解题,本文尝试从不同的切入点来分析解题思路,并给出几点启示.
2 问题呈现
已知x1、y1、x2、y2、x3、y3为六个不同的实数,满足①x1 A.2x2 分析1:由x1+y1=x2+y2=x3+y3知和为常数,设为k,再结合①、③两条件去推理. 评注:在代入③式后,使用基本不等式是解题的破冰之处. 分析2:不用基本不等式,也可通过作商比较大小的方法去处理. 分析3:考虑到x1+y1=x2+y2=x3+y3,也可换一个角度去假设. 评注:假设比较巧妙,解法简洁高效. 分析4:此题通过分析后,可根据其结构特点,通过构造函数去处理此题. 解法4:前同解法1,∵x1y1+x3y3=2x2y2,∴x1(k-x1)+x3(k-x3)=2x2(k-x2),构造函数f(x)=x(k-x),则上式 图1 评注:结合函数的图像去研究,显得直观易懂,体现了数形结合的解题思想. 分析5:此题如能同高数中函数凸凹性联系起来,则解题比较迅速. 评注:抓住函数的凸凹性去解题,简洁明了,比较节约时间. 分析6:选择题用特殊值法去解题,也可得到答案. 4.1高数背景 解法5用到了高数中的部分知识,是六种解法中较简单的.事实上近年来的高考题往往有高数的背景,如高数中的泰勒级数、等价无穷小、洛必达法则、拉格朗日中值定理等时有出现,掌握了这部分知识可以很快给出解答,比如下列这两道新课标高考题. A.a C.b 例2(2010新课标理解题)设f(x)=ex-1-x-ax2≥0对x∈[0,+∞)恒成立,求a的范围. 4.2追本溯源 本题求解对思维有较高要求,其命题背景也与教材有着紧密的联系,贯彻了高考命题源于教材高于教材的理念.一般地,本题的通法是构造函数,再结合函数的图像观察即可得.其来源于人教版数学选修2-2第32页B组第1题:证明下面不等式:(1)sinx 总之,加强“一题多解”的教学,既能培养学生的解题能力,又能使学生的核心素养的培养落地生根,且避免了学生陷入题海战术,从而收到良好的教学效果.正如罗增儒教授所言:“一个数学问题,如果我们只有一个解法,不管是自己想出来的还是翻答案看到的,都肯定会存在认识上的局限性,只有在得出二个或更多个解法之后,才会对问题的本质有真正的了解,通过解题而培养能力的目的也才有可能实现.”
3 解法赏析

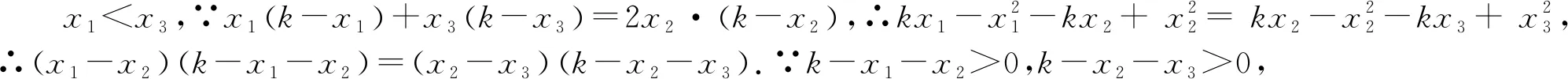
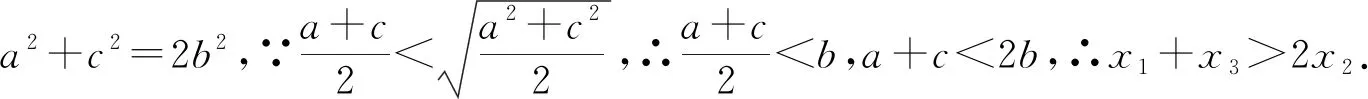
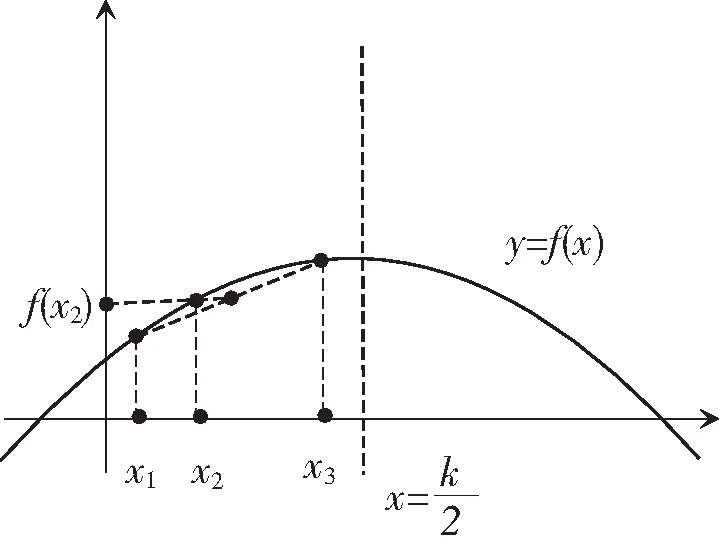

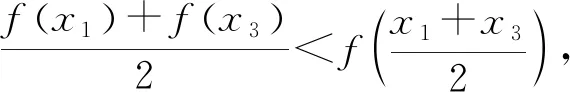
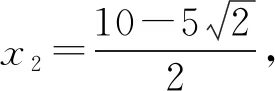
4 几点启示
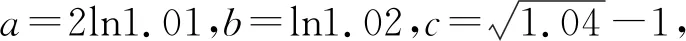
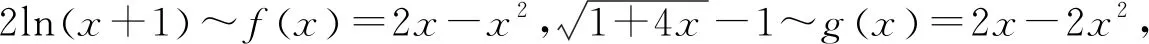
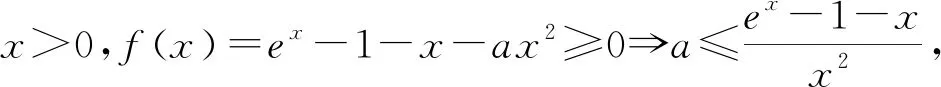
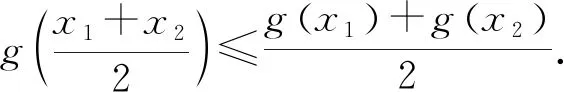
5 结语

