定日镜清洗过程中镜面振动的仿真分析

刘志娟，宓霄凌，李建华，王 伟

(1.浙江众晶软件开发有限公司，杭州 3100053；2.浙江中控太阳能技术有限公司，杭州 3100053)

0 引言

近年来，太阳能因具有清洁、安全、取之不尽、用之不竭等特点[1]，已成为各国力推的新能源形式。目前，太阳能发电主要有光伏发电和太阳能热发电这2种技术路径，其中，塔式太阳能热发电因具有发电效率高、电力品质好、可长时间蓄热、成本下降空间大等优势在近几年迅速崛起。

定日镜是塔式太阳能热发电系统中聚光系统的重要组成部分，是聚光系统进行能量收集和转化的基础性装备。由于定日镜镜面的清洁度会直接影响塔式太阳能热发电系统的发电效率[2]，因此，对定日镜进行周期性清洗是塔式太阳能热发电系统日常维护工作的主要内容之一。定日镜在清洗过程中势必会因受到清洗力的作用而发生一些位移和变形，由于其位移和变形难以通过直接测量的方式获得，因此长时间、定期清洗对定日镜的面型及精度造成的影响难以评估。基于此，本文提出了一套对定日镜清洗过程中镜面状态进行仿真的方案，以实际清洗过程中定日镜的受力状态为依据，利用有限元分析软件ANSYS Workbench中的模态分析法和瞬态动力学仿真模块对定日镜清洗过程中其镜面在受力状态下的变形量进行仿真计算。

1 定日镜清洗方案

随着塔式太阳能热发电技术的发展，作为塔式太阳能热发电系统的配套设施，定日镜清洗装置也在不断进步。然而由于塔式太阳能热发电系统中定日镜方案的多样性，当前尚未形成统一的定日镜清洗装置的方案和标准，通常是针对不同类型定日镜而定制的清洗装置方案。

定日镜的清洗作业通常采用冲洗、刷洗、刮洗等方式。浙江中控太阳能技术有限公司针对其定日镜产品的结构特点及其工作环境的气候特征，开发了一种集水洗和干洗功能于一体的清洗车[3-4]，如图1所示。该清洗车能实现对定日镜快速、高效地清洗。

图1 定日镜清洗车的实物图Fig.1 Photo of heliostat cleaning vehicle

从图1中可以看出，该清洗车的主要清洗部件为1个横向布置且能上下升降的刷辊，刷辊在清洗过程中除了可以上下升降外，还能进行自身的旋转运动。采用该清洗车时，1面定日镜的清洗过程为：定日镜转至清洗位姿(本文中的清洗位姿为定日镜镜面竖直放置)，清洗车行进至定日镜正前方，清洗车的刷辊升至镜面上部的边缘处，刷辊自身旋转，带动刷辊上的毛刷清洗镜面，同时刷辊在垂直方向由上向下运动，依次完成镜面上不同高度的清洗工作。

2 定日镜清洗过程中的仿真方案

利用ANSYS Workbench软件中的瞬态动力学仿真模块可以对定日镜的清洗过程进行仿真模拟，从而可以得到清洗过程中定日镜的变形数据，进而可对由清洗引起的镜面面型、光斑质量的变化等情况进行有效评估。

2.1 定日镜仿真模型

根据定日镜的实体结构，在SolidWorks三维设计软件中建立其3D模型。为消除非关键零部件对后续有限元仿真结果的影响，提升有限元分析结果的准确性，也为了控制有限元仿真模型的网格数量，因此对所建立的定日镜3D模型进行了适当修改与简化。为方便在仿真中模拟刷辊对镜面不同部位施加的压力，在3D模型中沿着刷辊运动方向将镜面横向划分为多个长条形的子镜面，并绑定在一起。修改与简化后的定日镜3D模型如图2所示。

图2 修改与简化后的定日镜3D模型Fig. 2 Modified and simplified 3D model of heliostat

2.2 定日镜清洗过程中的仿真

根据定日镜清洗过程的特性，选取有限元分析软件ANSYS Workbench中的瞬态动力学仿真模块对定日镜的清洗过程中的镜面状态进行仿真，建立定日镜的有限元仿真模型。建立完成后，可以得到单元集成总刚度矩阵[K]和总质量矩阵[M]，因此定日镜的动力学特性问题可转化为特征值的求解问题[5]，即：

式中：{Φi}为第i阶模态的振型向量(特征向量)；ωi为第i阶模态的固有频率；ωi2为固有频率的特征值。

有许多数值计算方法可用于求解式(1)，比如子空间迭代法和分块Lanczos法(即模态分析法)。子空间迭代法是利用广义的Jacobi迭代算法，并使用完整的质量和刚度矩阵，因此计算结果的精确度很高；但由于计算量大，计算速度会受到一定限制。分块Lanczos法以一组向量来实现Lanczos递归计算，计算结果的精确度高、计算速度更快。综合考虑后，本文中的动力学特性计算采用分块Lanczos法。

定日镜清洗过程中镜面状态的仿真流程图如图3所示。

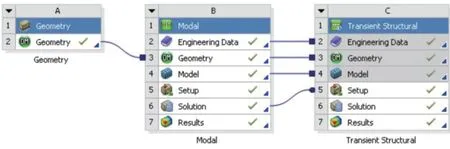
图3 定日镜清洗过程中镜面状态的仿真流程图Fig. 3 Simulation flow chart of mirror state during cleaning process of heliostat

定日镜清洗过程中镜面状态的仿真流程主要包括以下步骤：

1)在Engineer Data中编辑材料属性。由于定日镜镜面为玻璃材质，玻璃的弹性模量取7×1010N/m2，密度取2500 kg/m3，泊松比取0.215；其余结构的材质为结构钢，结构钢的弹性模量取2.1×1011N/m2，密度取7800 kg/m3，泊松比取0.3。

2)设置接触类型。本模型中使用默认的绑定接触即可。

3)网格的选取与划分。为获得较为精确的有限元分析结果，定日镜结构部件中尽量采用六面体网格进行划分，对关键部件进行局部细化，网格划分结果如图4所示。

图4 定日镜模型的网格划分结果Fig.4 Meshing result of heliostat model

4)设置约束及边界条件。根据定日镜安装使用的实际情况，对定日镜下半段立柱表面设置固定约束，如图5所示。

图 5 定日镜模型的约束设置Fig. 5 Constraint setting of heliostat model

5)施加荷载。清洗车在对定日镜进行清洗时，刷辊是自上而下依次刷遍整个镜面。清洗过程中，定日镜镜面承受的荷载可通过在镜面布置的贴片式压力传感器直接测得；然后根据清洗车上携带的刷辊在清洗过程中自身的旋转速度及刷辊自上而下的运动速度，可计算得到镜面各区域承受的刷辊施加的荷载的时间历程。

仿真中，根据清洗过程中定日镜镜面的受力情况，进行分区域、分时段的分步荷载施加。清洗刚开始时将清洗车刷辊的尺寸等面积对应到镜面自上边缘起的区域内，随着清洗过程中刷辊的自身旋转与向下移动，其与镜面的接触面积逐渐下移，直到刷辊与镜面的接触到达镜面下边缘区域时为最后一步。随后，刷辊会随清洗车的运动而离开被清洗镜面，并进入到下一面定日镜的清洗进程。清洗时第一步荷载的施加情况如图6所示，最后一步荷载的施加情况如图7所示。

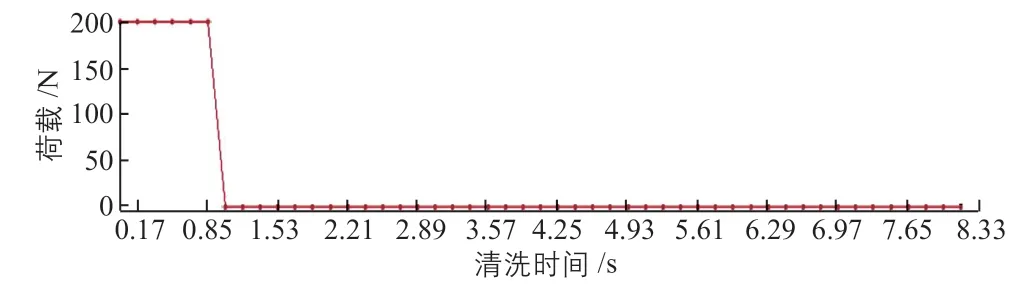
图6 第一步荷载的施加情况Fig. 6 First step of application of load

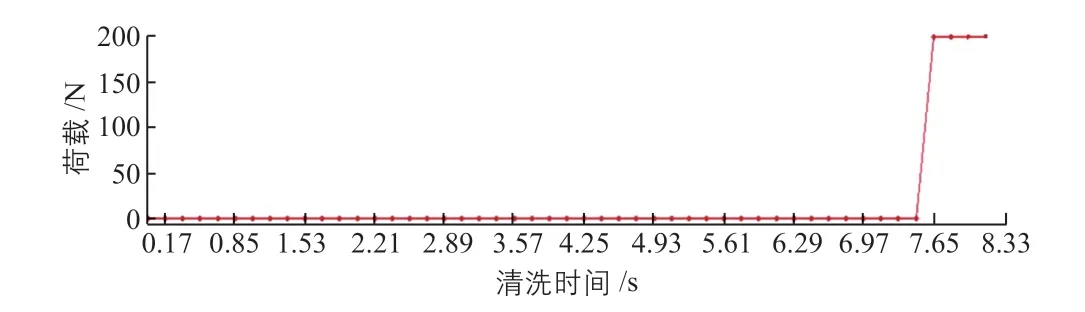
图7 最后一步荷载的施加情况Fig.7 Last step of application of load

3 定日镜清洗过程中的仿真结果与分析

3.1 模态分析结果

通过模态仿真计算，可得到定日镜前12阶模态的振动频率的仿真结果，如图8所示。

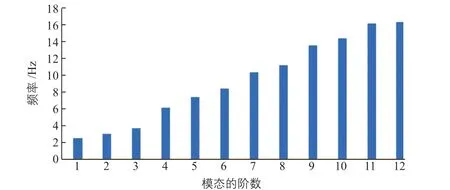
图8 定日镜前12阶模态的振动频率Fig.8 Vibration frequency of first 12-order modals of heliostat

从图8可以看出，前5阶模态的振动频率相对较低，在定日镜实际使用中应避免该段振动频率形成共振；此外，在基于模态分析法的瞬态动力学仿真中，前几阶模态的振型对最终瞬态动力学仿真结果产生的影响最大。因此下文对定日镜前5阶模态的振型进行分析。

定日镜前5阶模态的振型如图9～图13所示。

图9 定日镜第1阶模态的振型Fig. 9 Vibration shape of first-order modal of heliostat

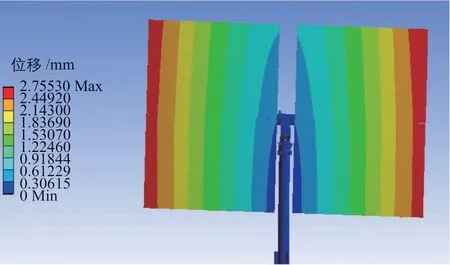
图10 定日镜第2阶模态的振型Fig. 10 Vibration shape of second-order modal of heliostat

图11 定日镜第3阶模态的振型Fig. 11 Vibration shape of third-order modal of heliostat

图12 定日镜第4阶模态的振型Fig. 12 Vibration shape of forth-order modal of heliostat

图13 定日镜第5阶模态的振型Fig.13 Vibration shape of fifth-order modal of heliostat

从图9～图13可以看出，定日镜前3阶模态的振型为定日镜整体变形，其中：第1阶模态的振型是以立柱为中心的一阶弯曲；第2阶模态的振型是镜体结构绕立柱(竖轴)的转动；第3阶模态的振型是镜体结构绕横轴的转动。而第4、5阶模态的振型是定日镜镜面外变形，其中：第4阶模态的振型是镜面下部变形量大于上部，第5阶模态的振型是镜面上下两端的变形量较大，中间的变形量较小。由于定日镜本身为对称结构，因此其各阶模态的振型也呈现一定的对称性。

3.2 振动与疲劳寿命的仿真结果

瞬态动力学仿真模块的仿真结果为定日镜清洗过程中的振动与变形量，定日镜清洗过程中第0.4 s时镜面的变形情况如图14所示。其中：图中的负号代表与刷辊作用力方向相反。

图 14 清洗过程中第0.4 s时镜面的变形情况Fig.14 Deformation of mirror at 0.4 s during cleaning process

从图14可以看出，在刷辊的冲击下，竖起的定日镜自上而下出现了不同幅值和不同方向的变形。其中：镜面上边沿的变形量接近9.5 mm；镜面下边沿的变形量约为-2.6 mm。

对1面定日镜整个清洗过程(0～8.16 s)中镜面在垂直方向上的变形量进行统计，变形量曲线如图15所示。其中，镜面变形量与刷辊作用力方向相同为正方向，反之则为反方向。

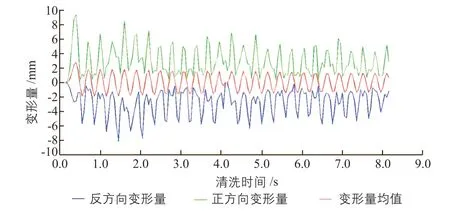
图15 定日镜清洗过程中镜面垂直方向上的变形量曲线Fig.15 Deformation curve in the vertical direction of mirror during cleaning process of heliostat

从图15中可以看出，在1面定日镜的完整清洗过程中，镜面在正方向上的最大变形量接近10 mm，在反方向上的最大变形量接近-8 mm，镜面的平均变形量基本在±2 mm范围内；镜面变形量随着刷辊自上而下的周期性冲击呈现出周期性的波动。由此可知，因清洗引起的定日镜镜体振动较为明显。

定日镜清洗过程中的总变形量曲线如图16所示。

图16 定日镜清洗过程中的总变形量曲线Fig.16 Total deformation curve of heliostat during cleaning process

4 实测验证

为进一步验证本文得到的因定日镜清洗引起的镜体振动的仿真结果的可靠性，利用某塔式太阳能热发电项目现场有限的实验条件，布置了1套测试系统，对定日镜清洗过程中镜面上某一位置的振动位移情况进行测试。测试系统的布置方法为：在定日镜背面靠近边缘位置选取1个测试点，在该测试点处粘贴1台激光发射器，在被测定日镜正后方远处固定1块白板用于呈现激光发射器发出的激光光斑，在白板前方设置1台固定摄像机，实时拍摄白板上激光光斑的位置影像。测试系统的构成示意图如图17所示。

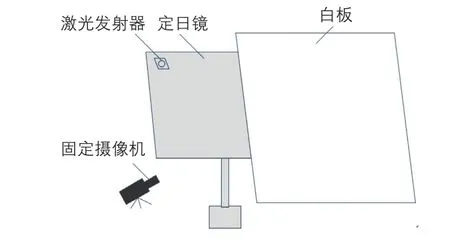
图17 测试系统的构成示意图Fig.17 Schematic diagram of composition of test system

在定日镜清洗过程中，通过固定摄像机连续实时拍摄安装于定日镜背面的激光发射器投射到白板上的光斑影像，清洗完成后利用图像处理技术对拍摄的激光光斑影像进行处理，可得到激光光斑在白板上的位置变化轨迹。具体实现过程为：在定日镜清洗前，将激光发射器投射到白板上的光斑位置设定为原点，被测定日镜镜面与白板平行，二者之间的直线距离可通过测量获得；在拍摄的激光光斑影像中，对每步荷载对应的该时刻下的光斑图像进行截取，然后通过光斑图像与原点位置的偏移方向和偏移距离，以及被测镜面与白板之间的直线距离，根据余弦定理可以计算出被测镜面的旋转角度，该角度与镜面清洗振动前后的扭转角度一致；再根据测试点与镜面旋转中心之间的距离，可以计算出测试点在每一步荷载施加时的变形量和变形方向(将与镜面垂直方向定义为正或定义为负)。将定日镜背面测试点在实际清洗过程中的位移数据与以该测试点作为仿真节点时得到的位移数据进行对比，对比结果如图18所示。

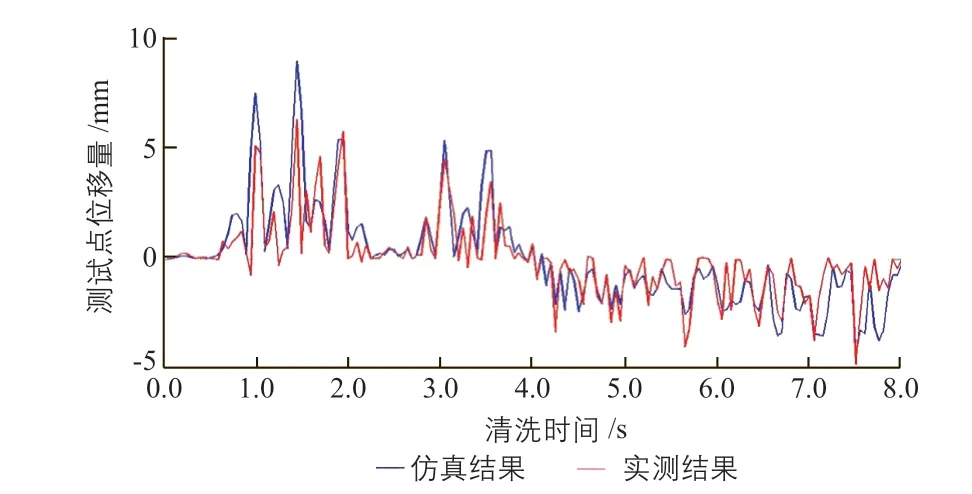
图18 定日镜清洗过程中测试点位移量的实测结果与仿真结果对比Fig. 18 Comparison between measured and simulated results of displacement of test point during cleaning process of heliostat

由图18可知，在清洗过程中，定日镜背面测试点位移量的实测结果曲线与仿真结果曲线的变化趋势一致，位移量接近，说明仿真结果与实测结果的匹配度较高，仅存在局部差异，该差异可能来源于测试过程中的拍摄延时、非线性误差、测量误差，以及测试方法本身的近似估算误差。

5 结论

在塔式太阳能热发电站中，定日镜清洗是维持定日镜镜面清洁度、保证镜场光热转换效率必不可少的工作。本文提出了一种基于ANSYS Workbench有限元分析软件的定日镜清洗过程中镜面状态的仿真方案，利用模态分析法和瞬态动力学仿真模块，模拟定日镜清洗过程中镜面的受力情况，获取因清洗引起的镜面变形情况，为定日镜结构优化、清洗方案优化等提供了数据依据。经实验测试，利用本文提出的仿真方案得出的定日镜背面测试点位移量的仿真结果曲线与实测结果曲线具有较高的匹配度。