基于旋转阀的钻井液连续波抗波形失真的信号调制优化研究
庞东晓,蔡文博,陈 倩,喻著成,徐建超
1中国石油集团川庆钻探工程有限公司钻采工程技术研究院 2西南石油大学机电工程学院 3中国石油集团川庆钻探工程有限公司
0 引言
随着油气勘探开发向数字化、智能化进军,各种井下新型测量仪器层出不穷,测量参数也从随钻井斜、方位等几何参数发展到钻压、振动等多个工程、地质参数,在水平井、大位移井的开采过程中,实时了解井下信息能够有效地提高石油天然气的开采效率[1]。现有的数据传输方式主要以负脉冲、正脉冲和连续波为主,其中连续波传输技术以脉冲发生器为载体,以正弦压力波为载波,以地面测得的立管压力波信号为调制信号,通过对波形幅度、频率或相位的调制恢复出井下数据。该技术具有传输速率高、可靠性好、综合性价比高等优点,成为随钻测量技术和钻井液井下数据传输系统发展的前沿方向[2]。国内研究的连续波脉冲发生器传输速率难以满足工程作业的需求,已成为随钻测量及测井领域持续向前发展的瓶颈[3- 4]。
常见调制方式有频移键控(FSK)[5]、最小频移键控(MSK)[6]、二进制相移键控(2PSK)[7]、差分相移键控(DPSK)[8]和正交相移键控(QPSK)[9]。上述调制方式都是无线通信中常见的数字调制方式,但应用到钻井液连续波脉冲系统时,由于连续波脉冲发生器的控制比较复杂,特别是对电机的动态性能要求较高,发射波形易出现一定程度的失真,从而影响接收机解调的误码率[10]。钻井液连续波脉冲发生器中压力波信号是由旋转阀转动后间歇性开关产生的,理想的压力波信号为正弦信号,为实现高传输速率,要求旋转阀按一定规律加减速旋转并达到一定的控制精度要求,进而产生理想的压力波信号,但机械装置受惯性影响,控制精度与旋转阀产生理想正弦波之间的关系是未知的,因此需要对转阀控制逻辑导致产生码元过渡时间,载频误差和相位漂移的原因进行研究[11- 13]。
针对不同失真模型各种调制方式的误码率,研究人员进行了很多研究。沈跃等[14- 15]人考虑的波形失真模型表示为一种幅度调制失真,即将失真效果表现为一种载频附近具有快慢变化随机振幅与随机相位的简谐振荡,并以此为基础探讨了这种波形失真对DPSK调制方式的误码率影响。路林林等[16]人考虑的波形失真模型为谐波失真,即调制过程中产生的高频谐波分量,对DPSK调制方式的误码率的影响。上述研究虽提出了几种调制方式对误码率的影响,但对于转阀控制研究来说,未提出明确的高传输速率下的控制精度要求[17- 18]。因此,本文针对不同调制方式的误码率性能,重新定义了波形失真,并对2FSK、2PSK和QPSK三种调制方式的误码率性能进行了比较分析,给出了三种调制方式对于波形失真的容忍程度,评估了码元过渡时间,载波误差和相位漂移对误码率的影响,为转阀控制提供依据。
1 压力信号解调数学模型
以二进制调制方案为例,无论是2FSK还是2PSK调制方式,都可以统一的将发射波形表示成如下形式:
(1)
根据最佳接收机理论[12]可知,在高斯白噪声干扰下要获得最低的误码率,可采用如下的接收机:
(2)
最后对R0和R1比较大小,来确定发射比特,即
(3)
在高斯白噪声干扰条件下,设信噪比为
(4)
式中:r—发射信号,V;t—时间,s;R—接收信号功率,V;Eb—每一个比特码元能量,J;n0—噪声功率谱密度,W/Hz。
根据上述原理,可得到2FSK、2PSK和QPSK的解调方案和误码率,如表1所示。

表1 不同调制下误码率计算表
2 钻进液压力波失真诱因与机理
2.1 钻井液压力波产生机理
旋转阀由定子和转子组成,如图1所示本文以四叶片旋转阀进行讨论 ,在位置A处转子完全挡住流道,实现全闭状态,出现压力波峰,在位置B处流道完全打开,实现全开状态,出现压力波谷。转阀从全闭(位置A)到全开(位置B)转过的角度为45°,由位置A到位置C转过90°产生一个完整的波形,地面通过检测压力波形,将压力波形进行转换即可进行数据传递[19]。
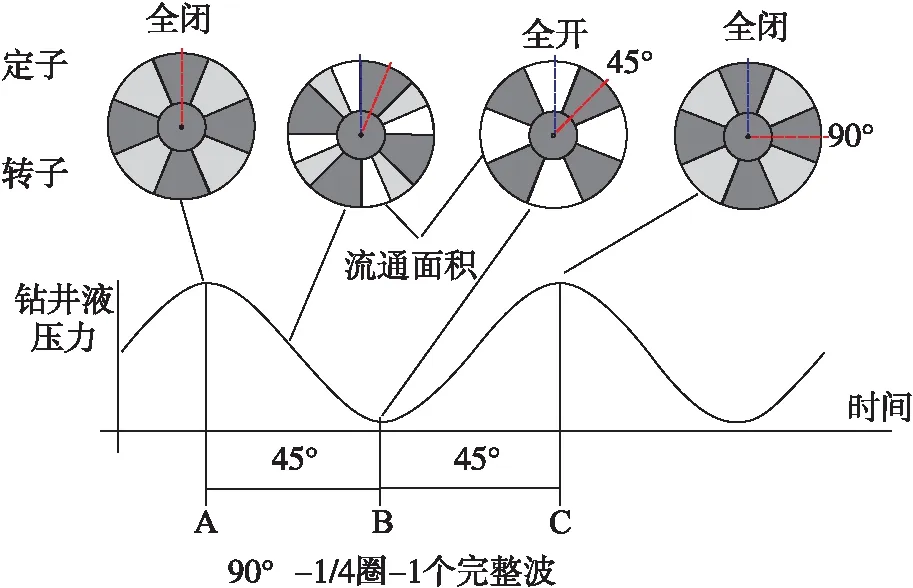
图1 压力波产生原理图
假设压力波为1Hz,由频率和周期关系式f=1/T可知,T=1 s,转阀旋转360°会产生四个完整的波形,即四个周期,则转阀圈数T1=4T=4 s,因此可知1 s转1/4圈,故1 Hz情况下所需旋转阀转速为0.25 r/s,即15 r/min;同理可得不同频率下的传输速率如表2所示。此外,为实现更好的信号传输,旋转阀产生的压力波需为理想正弦波,要想达到传输速率10 bit/s,需在一个压力波周期内(本文条件下即为0.025 s内),实现如正弦波一样的加减速度控制,难度极高。

表2 四个波形表示一个码元周期关系对比图
2.2 压力波码元过渡时间
假设正常码元波形表示为s(t),过渡波形表示为x(t),码元持续时间表示为T,过渡时间长度为τ,则码元过渡时间导致的失真波形d(t)可定义为:
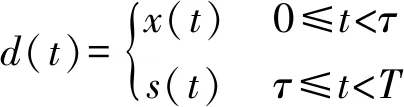
(5)
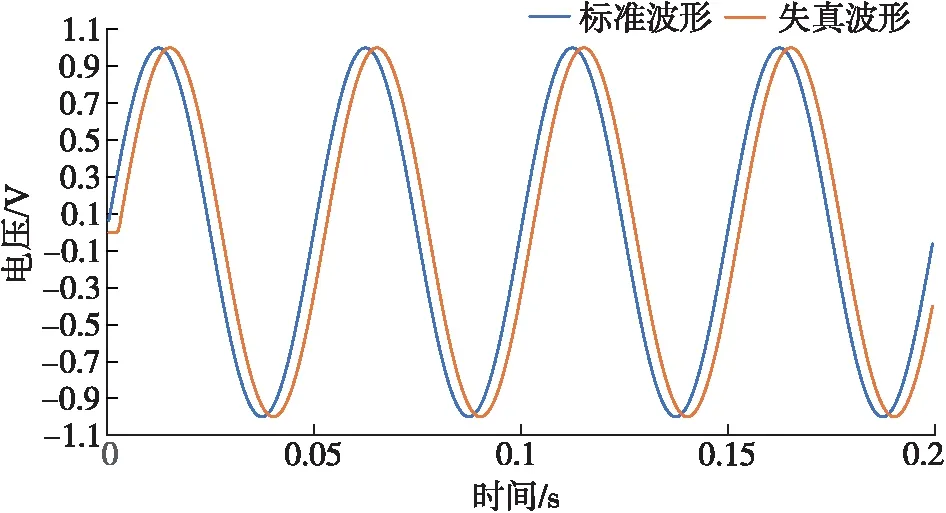
压力波的产生受机械装置控制,受惯性的影响,电机在启动时存在加速时间,实际调制波形过程会存在一定程度的失真。电机启动时的加速时间波形如图2所示,蓝色曲线是标准正弦波形,对应载波频率为20 Hz,码元速率为5 bit/s,持续时间为0.2 s;红色曲线是存在码元过渡时间的情况,码元过渡时间为0.05 s,用于模拟电机的加速时间。显然,在码元过渡时间中码元波形存在明显失真,码元切换时刻波形混乱,这部分波形能量无法用于接收匹配滤波中,从而导致系统误码率增加。
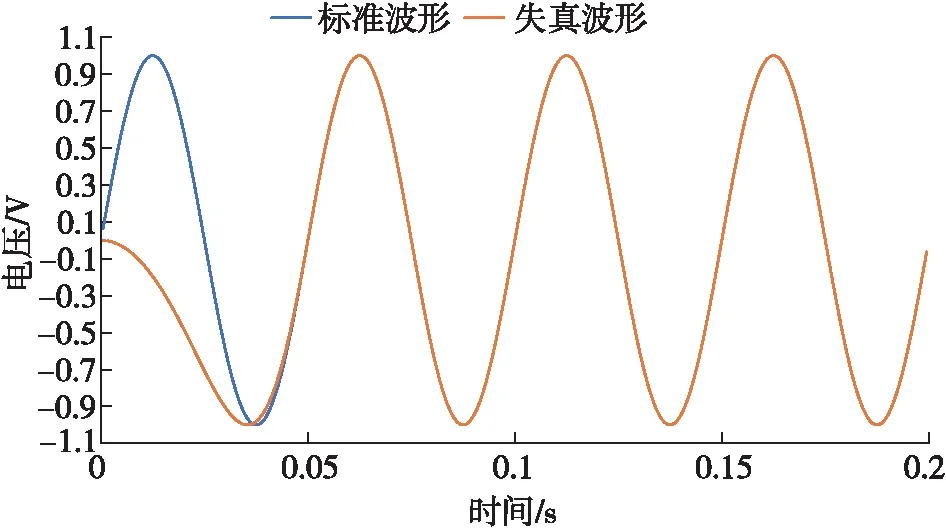
图2 码元过渡时间导致的失真波形的影响
2.3 压力波载频稳定度
假设正常码元波形表示为s(t)=sin(2πfct),频率抖动fd为一个随机变量,在范围-Fd~Fd之间均匀分布,则压力波载频稳定度导致的失真波形d(t)可定义为:
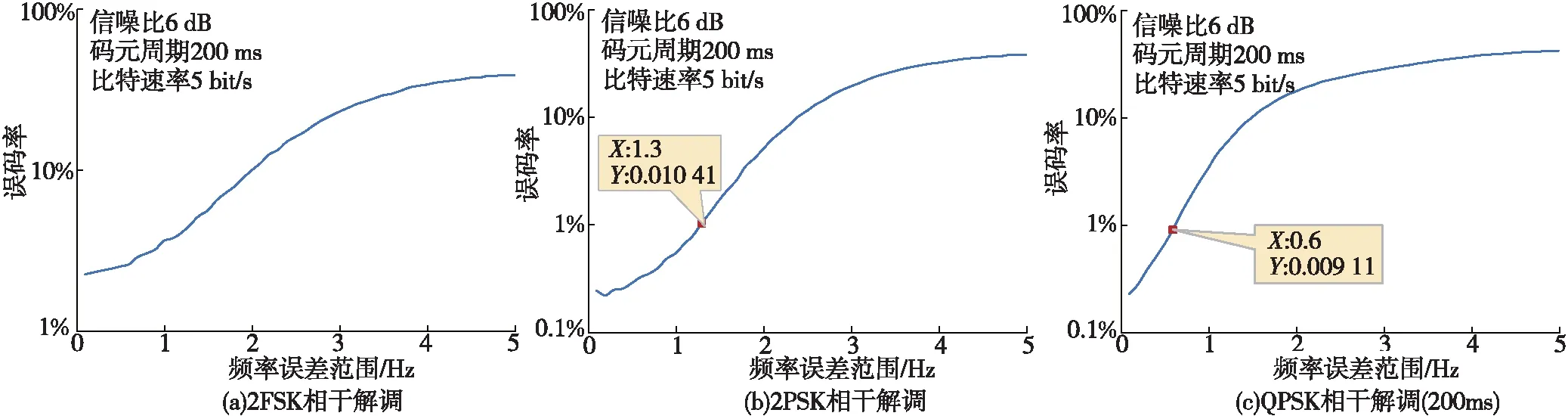
d(t)=sin2π(fc+fd)t0≤t (6) 在理想情况下,电机匀速旋转可产生理想的正弦波,但实际工况下,由于机械装置受到井筒内钻井液阻力及电机驱动等非理想因素影响,电机转速会存在一定的波动和偏差。图3为波动导致的正弦波频率失真图,其中蓝色曲线是标准正弦波形,对应载波频率为20 Hz,码元速率为5 bit/s,持续时间为0.2 s;红色曲线是存在载波频率抖动的情况,频率抖动的最大值为0.8 Hz,用于模拟电机转速波动。由于频率抖动会造成码元波形与理想波形之间形成明显的相位差,对于通信系统而言,这意味着在进行相干解调时无法完全对齐,导致部分波形能量损失,从而导致系统的误码率增加。显然,频率抖动范围越大,码元波形与理想波形之间的差距也会变大,导致通信系统性能下降。 图3 频率不稳定导致的失真波形的影响 假设正常码元波形表示为s(t)=sin(2πfct),相位漂移pd为一个随机变量,在范围-Pd~Pd之间均匀分布,则相位漂移导致的失真波形d(t)可定义为: d(t)=sin(2πfct+pd) 0≤t (7) 电机如果对启动时间控制得非常精确,产生的正弦波零相位会处于码元起始时刻。但实际情况是由于电机运动与压力变化之间存在一定延迟,电机对于正弦波的初始相位控制存在一定误差,尤其是对于相位调制信号,这种误差会对系统性能造成明显影响,如图4所示。 图4 相位偏移导致的失真波形的影响 图4中蓝色曲线是标准正弦波形,对应载波频率为20 Hz,码元速率为5 bit/s的一个码元波形,持续时间为0.2 s;红色曲线是存在相位漂移20°的情况,用于模拟电机运动与压力波变化的滞后效应。显然,由于相位漂移会造成码元波形与理想波形之间形成明显的相位差,对于通信系统而言,这意味着在进行相干解调时无法完全对齐,导致部分波形能量损失,从而导致系统的误码率增加。相位漂移范围越大,码元波形与理想波形之间的差距也会变大,导致通信系统性能下降。 针对码元过渡时间失真、载频稳定度失真和相位漂移失真三种不同的波形失真模型,采用蒙特卡洛仿真的方式分析它们对2FSK、2PSK和QPSK调制方式误码率的影响,研究误码率控制在1%以内时不同类型波形失真的容忍程度,参数设置如表3所示。 表3 仿真参数设置 压力波码元过渡时间对不同信号误码率的影响如图5所示。从图5可以看出,在6 dB的信噪比下,2FSK信号在理想情况下也无法达到控制在1%以内的误码率;2PSK信号要达到控制在1%以内的误码率需码元过渡时间控制在67 ms以下;QPSK信号要达到控制在1%以内的误码率,在码元周期为200 ms时码元过渡时间需控制在63 ms以下。 图5 不同码元过渡时间下的误码率仿真结果 压力波载频稳定度对于不同信号误码率的影响如图6所示。从图6可以看出,在6 dB的信噪比下,2FSK信号即使是理想情况下也无法达到控制在1%以内的误码率;2PSK信号要达到控制在1%以内的误码率需码载频误差范围控制在1.3 Hz以下;QPSK信号要达到控制在1%以内的误码率,在码元周期为200 ms时载频误差需控制在0.6 Hz以下。 压力波相位漂移对于不同信号误码率的影响如图7所示。从图7可以看出,在6 dB的信噪比下,2FSK信号即使是理想情况下也无法达到控制在1%以内的误码率;2PSK信号要达到控制在1%以内的误码率需相位漂移控制在52°以内;QPSK信号要达到控制在1%以内的误码率,码元周期为200 m时,相位漂移都需控制在22°以内。 图6 不同频率误差范围下的误码率仿真结果 图7 不同相位偏移下的误码率仿真结果 (1)脉冲发生器中高速转动的转阀要求高,特别是微秒级摆动时,惯性作用下的精确速度控制对控制逻辑、控制精度提出了更高的要求,控制逻辑、控制精度不满足要求,将导致码元过渡时间、载频误差,相位漂移出现偏差,编解码困难。 (2)在载波频率为20 Hz,信号传输速率为5 bit/s的调制参数下,在信噪比为6 dB的情况下,只有2PSK和QPSK才能达到控制在1%以内的误码率性能,但QPSK调制的传输速率要比2PSK快一倍,且 QPSK调制在10 bit/s的速率下也能达到够控制在1%以内的误码率性能,因此更适用于高速率传输的应用场合。 (3)在6 dB的信噪比下,要达到控制在1%以内的误码率,2PSK信号中码元过渡时间需控制在67 ms以下,载频误差范围需控制在1.3 Hz以下,相位漂移控制在52°以内。QPSK信号中码元周期为200 ms时,码元过渡时间需控制在63 ms以下,载频误差需控制在0.6 Hz以下。若不能达到上述条件则无法解调。 (4)在6 dB的信噪比下,要达到1%的误码率,QPSK信号中码元周期为200 ms时,相位漂移都需控制在22°以内,否则将无法解调。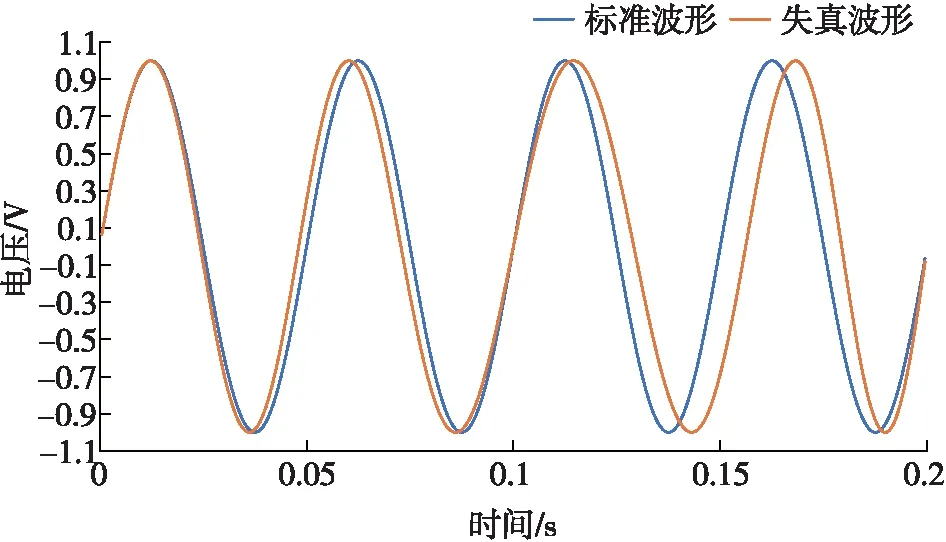
2.4 压力波相位漂移
3 压力波失真仿真分析

3.1 压力波码元过渡时间

3.2 压力波载频稳定度
3.3 压力波相位漂移

4 结论

