INFLUENCE OF DAMPING MODELS ON DYNAMIC ANALYSES OF A BASE-ISOLATED COMPOSITE STRUCTURE UNDER EARTHQUAKES AND ENVIRONMENTAL VIBRATIONS
FEI Yi-fan , TIAN Yuan , HUANG Yu-li , LU Xin-zheng
(Key Laboratory of Civil Engineering Safety and Durability of China Education Ministry,Department of Civil Engineering, Tsinghua University, Beijing 100084, China)
Abstract: Structural design simultaneously governed by earthquakes and environmental vibrations has received a lot of attention in recent years. Base-isolated composite structures are typically used in the above-mentioned structural design. The corresponding analysis involves validating structural safety under earthquakes and human comfort under environmental vibrations through a time-history analysis. Thus, a reasonable damping model is essential. In this work, the representatives of viscous damping model and rate-independent damping model,namely the Rayleigh damping model and uniform damping model, were adopted to investigate the influence of damping models on the time-history analysis of such structural designs. The energy dissipation characteristics of the above-mentioned damping models were illustrated via a dynamic test of recycled aggregate concrete specimens. A case study was performed on a base-isolated steelconcrete composite structure. The dynamic responses under the excitation of earthquakes and environmental vibrations were compared using different damping models. The uniform damping model was found to be more flexible than the Rayleigh damping model in dealing with excitations with different frequency components. The uniform damping model is both theoretically advantageous and easy to use, demonstrating its potential in dynamic analysis of structures designed simultaneously governed by earthquakes and environmental vibrations.
Key words: seismic and environmental vibration analysis; Rayleigh damping model; uniform damping model;seismic isolation; composite structure
1 Introduction
In recent years, China has witnessed rapid developments in civil engineering. New building structures located next to high-speed railways or subways should be constructed in line with the requirements for both seismic safety and environmental vibration control[1-3]. Considering both earthquakes and environmental vibrations during the structural design is particularly important for some buildings, such as laboratories that have precision equipment, as well as office buildings, hotels, and hospitals with high comfort requirements.
Structural design simultaneously governed by earthquakes and environmental vibrations not only ensures seismic safety but also supports environmental vibration control. Thus, a corresponding dynamic analysis is necessary to validate the design results. Time-history analysis has become an important method for evaluating seismic safety and simulating environmental vibrations[4-6].The results of the analysis are significantly influenced by the characteristics of the selected damping model.In the existing literature, the Rayleigh damping model[7-9]and the Wilson–Penzien damping model(the superposition of modal damping)[10-11]are most commonly utilized for dynamic analysis. Many new damping models[12-14]have also been proposed to address the weaknesses of existing damping models in dynamic analysis.
A base-isolated composite structure is a common structural type. The dynamic analysis of this structure under earthquakes and environmental vibrations has the following characteristics: 1) Earthquakes and environmental vibrations have different frequency components that can excite different vibration modes of the structure. Accordingly, the damping model should reasonably consider the contributions of all excited modes. 2) The damping model should avoid introducing “spurious” damping forces to rigidbody motions, which are significant in the horizontal response of base-isolated structures. 3) The composite structure is composed of various materials with different damping characteristics. Therefore, the damping model should reasonably reflect the damping characteristics of different materials. However, owing to the lack of relevant analysis, the effect of damping models on the dynamic analyses remains unclear.
This work first introduces a typical viscous damping model (i.e., Rayleigh damping model) and a novel rate-independent damping model (i.e., uniform damping model). The energy dissipation of different damping models under various loading frequencies is then illustrated based on the dynamic test of recycled aggregate concrete specimens. Next, a case study is conducted on a base-isolated steel–concrete composite structure to explore the effects of different damping models on the structural dynamic analyses under earthquakes and environmental vibrations. Finally, the critical issues are summarized regarding the use of the above-mentioned damping models in dynamic analysis considering earthquakes and environmental vibrations.
2 Damping models
2.1 Rayleigh damping model
Owing to its simplicity, the Rayleigh damping model has been widely used in seismic and environmental vibration analyses[15-18]. For the equation of motion shown in Equation (1), the viscous damping force is formulated as Equation (2):

wherefIrepresents the inertial force;fDrepresents the damping force;f0denotes the restoring force;pdenotes the external force;Cis the viscous damping matrix; anduis the displacement vector. The Rayleigh damping model can be expressed as a linear combination of the mass and stiffness matrices, as shown in Equation (3)[19]:

whereMandKare the mass and stiffness matrices,respectively; the coefficientsa0anda1can be determined using Equation (4):
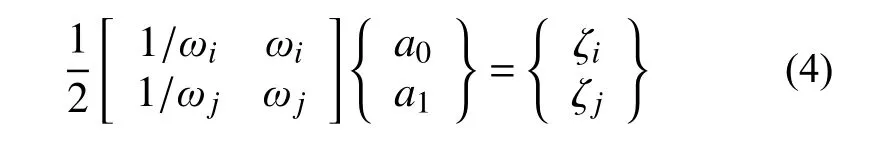
whereωi(ωj) and ζi(ζj) are the natural frequency and damping ratio of thei-th (j-th) mode, respectively.
Note that the Rayleigh damping model is defined according to the damping energy dissipation of each mode at the natural frequency. In the application, the viscous damping ratio of each mode is defined. The overall damping behavior of a structure is mainly determined by the proportion of each mode in the actual vibration and the corresponding predefined viscous damping ratio. However, because the Rayleigh damping model is based on the viscous damping theory, the energy dissipation caused by the viscous damping ratio of each mode is proportional to the actual vibration frequency of the corresponding mode.
In Figure 1(a) for example, given thei-th andj-th natural frequencies and viscous damping ratios, the viscous damping ratio of each mode of the Rayleigh damping model is fully determined. The Rayleigh damping model underestimates the viscous damping ratios of the modes between thei-th andj-th modes and significantly overestimates the viscous damping ratios of the other modes. Moreover, owing to its inherent theoretical deficiency of the viscous damping model, the energy dissipation of each mode is proportional to its actual vibration frequency, as shown in Figure 1(b), which is inconsistent with the phenomena typically observed in the dynamic tests of solid structures.

Fig. 1 Schematics of Rayleigh and uniform damping models
2.2 Uniform damping model
Huang et al.[20]proposed a novel uniform damping model that ensures frequency-independent energy dissipation over a specified vibration frequency range. Specifically, the damping forcefDis formulated using Equation (5):
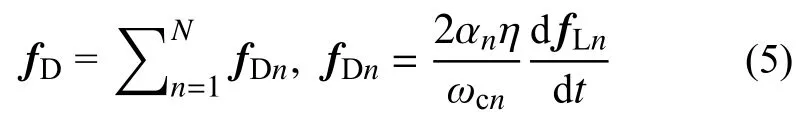
where αnis then-th item of the adjustment factors α=[α1, ··· ,αN]T; η is the target loss factor that represents the energy dissipation capacity (ratio between damping energy dissipation and strain energy);ωcnis then-th cutoff frequency, and a totalNnumber of cutoff frequencies are logarithmically spaced in the specified frequency range (including endpoints). Additionally,fLnis the time history of the restoring force through a low-pass filter with the cutoff frequencyωcn; it follows Equations (6) and (7):

When Equation (8) is satisfied, rate-independent damping models and viscous damping models dissipate the same amount of energy at the vibration frequencyω, where ζ is the viscous damping ratio,andωnis the natural frequency of the vibration mode.

Figure 1(b) shows the relationship between the energy dissipation induced by the uniform damping model and the vibration frequency. Compared with the Rayleigh damping model, the energy dissipation of the uniform damping model remains largely unchanged in the specified frequency range, which is close to the experimental phenomena. Note that uniform damping is defined according to the damping energy dissipation corresponding to each vibration frequency in the frequency range. Therefore, the energy dissipation of each mode at the actual vibration frequency can be ensured as long as the main vibration frequencies of the structure are covered by the defined frequency range.
3 Comparison of energy dissipation of different damping models
3.1 Case information
To further demonstrate the energy dissipation characteristics of the Rayleigh damping model and uniform damping model, the dynamic test for recycled aggregate concrete by Liang et al.[21]was selected. The loss factors of the R0 specimen at different loading frequencies were analyzed. The recycled aggregate concrete specimen had a diameter of 100 mm and height of 200 mm. Cyclic compressive loading was applied to the specimen in the axial direction with a minimum force of 2 kN and a maximum force of 60 kN. The specimen remained elastic during the entire loading process. The loading frequency was adjusted to 1.0 Hz, 0.5 Hz, 0.2 Hz and 0.05 Hz,respectively. Among them, a compressive loading of 1.0 Hz was applied for 30 cycles, and those of the other frequencies were applied for five cycles. For details, please refer to Liang et al.[21].
Liang et al.[21]found that the R0 specimen exhibited an approximate energy dissipation capacity at different loading frequencies. The loss factors at different loading frequencies are listed in Table 1.

Table 1 Test results of loss factors of R0 specimen
3.2 Model establishment
According to Liang et al.[21], the specimen remained elastic during the entire loading process.Therefore, the elastic beam element was used for simulation in the Open System for Earthquake Engineering Simulation (OpenSees)[22], which is an open-source software framework for finite element analysis.
1) Uniform damping model
According to the experimental data in Table 1, a constant loss factor was set within the specified frequency range. To ensure that the damping energy dissipation in the entire loading frequency range was as close as possible to the test, the experimental loss factor corresponding to the 0.2 Hz loading frequency(Table 1) was selected for the entire loading process.
2) Rayleigh damping model
Two natural frequencies and the corresponding viscous damping ratios must be defined for the Rayleigh damping model. Considering the deformation characteristics of the specimen, the given damping ratio was defined as being satisfied in the 1st and the 3rd modes. Specifically, the deformation was dominated by the 1st mode, and only the damping ratio in the 1st mode needed to be satisfied. Owing to the small specimen size, the natural frequency of the 1st axial mode was very large (above 3500 Hz), which was far from the actual vibration frequency.Therefore, Equation (8) was adopted to calculate the equivalent viscous damping ratio corresponding to each mode.
Only one set of Rayleigh damping parameters can be defined during the entire loading process. To ensure that the damping energy dissipation in the loading frequency range (0.05~1.0 Hz) was as close as possible to the test,ωwas taken as 0.2 Hz in Equation(8), and η was taken as the corresponding experimental loss factor.
3.3 Simulation results
Figure 2 compares the loss factors simulated by different damping models to the experimental results.

Fig. 2 Comparison between the simulated and experimental loss factors
When the uniform damping model was used, the distribution of the loss factors in the frequency domain could be accurately simulated (relative error between -4.0% and 7.2%). When using the Rayleigh damping model, because the model was defined according to the damping characteristics at 0.2 Hz, the loss factor under 0.2 Hz excitation was largely consistent with that in the experiment. However,owing to the inherent deficiency of viscous damping models, the damping energy dissipation is proportional to the vibration frequency. Therefore, the loss factor under 1.0 Hz excitation was approximately five times that under 0.2 Hz excitation. The relative errors between the simulation results and the test results were between -76.0% and 455.5%.
Therefore, the uniform damping model has significant advantages over the Rayleigh damping model in analysis tasks with a large vibration frequency range. In structural design simultaneously governed by earthquakes and environmental vibrations, external excitations, especially in environmental vibration analysis, cover a wide frequency domain. Hence, the adoption of a uniform damping model in these analyses is reasonable.
4 Dynamic analysis of a baseisolated composite structure
4.1 Case information

Fig. 3 Basic information of the steel–concrete composite structure
This study adopted a five-story steel–concrete composite structure[23]to investigate the influence of damping models on the dynamic analyses of baseisolated composite structures under earthquakes and environmental vibrations. Basic information on the structure is presented in Figure 3. The specific dimensions of the steel sections are listed in Tables 2 and 3. The building has four bays in both theXandYdirections, each with a size of 6 m. The height of the first floor is 4 m, and that of the remaining floors is 3 m. Both beams and columns adopt H-shaped steels.Hollow structural steels are used as braces (placed only at axes ① and ⑤). The floor system consists of steel–concrete composite slabs. Lead rubber bearings(LRBs) are applied at the bottom of all the columns of the building, and their properties are listed in Table 4.The properties of the concrete and steel materials are listed in Table 5. For other properties, readers may refer to Providakis[23].
Table 2 Dimensions of the H-shaped steels /mm

Table 3 Dimensions of the hollow structural steels /mm
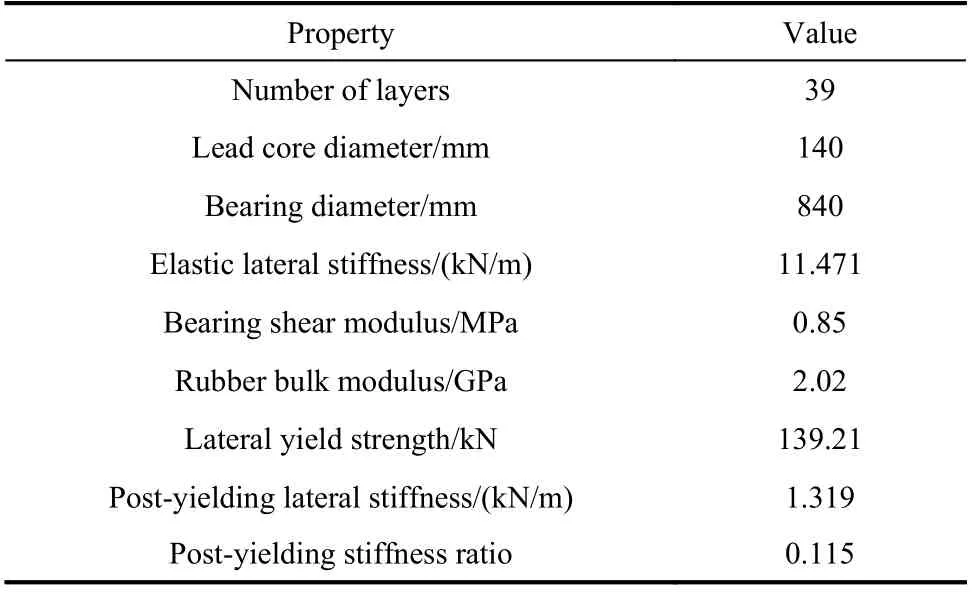
Table 4 Properties of the lead rubber bearing

Table 5 Material properties[23]
4.2 Model establishment
The finite element model of the structure was built using OpenSees.Fibersections were used for beams, columns, and braces. The upper and lower parts of the composite slabs were separately modeled[24]. The upper part (with uniform thickness)was modeled with theLayeredShellsection (i.e., the multilayered shell)[25], whereas the concrete ribs and corrugated steel sheets in the lower part were modeled with theFibersections, as shown in Figure 4.Interactions between the upper and lower parts of the floors and steel beams were considered by sharing the nodes. Their vertical spatial positions were defined by joint offsets (“jntOffset”). The LRBs were modeled by theLeadRubberXelement[26], which uses six springs to consider the mechanical behavior in the directions of six degrees of freedom. Among them, the constitutive model in the axial direction can simulate buckling in compression, coupling of horizontal and vertical motion, cavitation and post-cavitation behavior in tension, and strength degradation in cyclic tensile loading[26]; the constitutive model in the shear direction adopts the extended Bouc–Wen model and considers the strength degradation behavior[27-28].This element can reflect the strength degradation in cyclic shear loading owing to the heating of the lead core[26]. The element and section commands used are listed in Table 6. Concrete01 and Steel02 were selected as the material classes for concrete and steel,respectively.

Fig. 4 Modeling of the composite slab
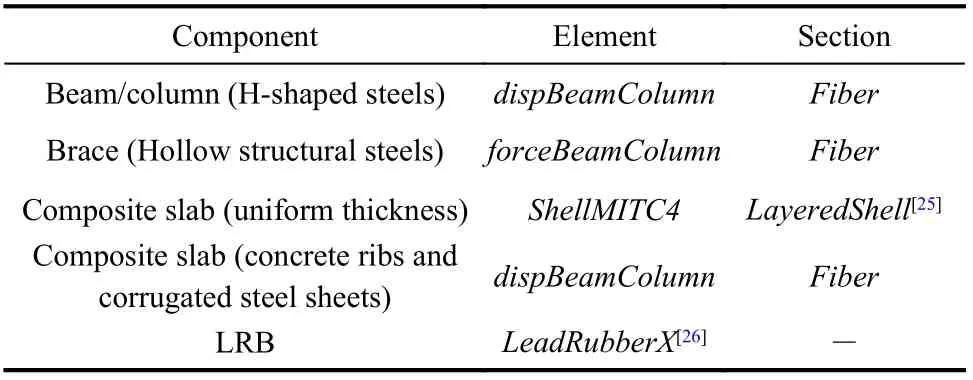
Table 6 Element and section commands for components
Figure 5 shows the established finite element models. Figure 5 shows the full model for seismic analysis with a maximum shell element size of 1.2 m.Figure 5(b) shows the 1/4 symmetrical model for the environmental vibration analysis with a maximum shell element size of 0.3 m. The latter model can consider vibrations of up to 100 Hz[29-30]. According to the modal analysis results, the natural periods of the structure before and after base-isolation along theXaxis were 0.46 s and 0.96 s, respectively. The natural period after base isolation was obtained after the application of gravity. The corresponding average vertical displacement of the LRBs was 7.5 mm.

Fig. 5 Finite element models
4.3 Seismic analysis
The El Centro ground motion was input into the structure along theXaxis, and the peak ground acceleration was amplified to 0.7 m/s2. The basic information of the investigated cases is presented in Table 7. The Rayleigh damping model was defined using the 1st and the 3rd translational mode of the structure along theXdirection[7,31]. The frequency range of the uniform damping model covered the main translational modes of the structure along theXdirection. To speed up the simulation, theExpressNewtonalgorithm[32]was used, which is highly efficient. The time step was taken as 0.01 s.

Table 7 Seismic analysis cases
The inter-story drift ratios (IDRs) and peak floor accelerations (PFAs) before and after seismic isolation are shown in Figure 6. The IDRs and PFAs are significantly reduced with the application of LRBs.The selection of the damping model has a larger influence on the response of the superstructure before seismic isolation.

Fig. 6 Seismic responses before and after base-isolation
Figure 7 shows the responses of the base-isolated structure using different damping schemes. The results suggest:
1) Owing to the existence of LRBs, the superstructure hardly deforms (the maximum IDR is less than 0.1%). The deformation mainly occurs in the LRBs, and the influence of damping models can be reflected in the deformation of the LRBs. It can be seen from Table 8 that the deformation is the smallest when the Rayleigh damping model is used.
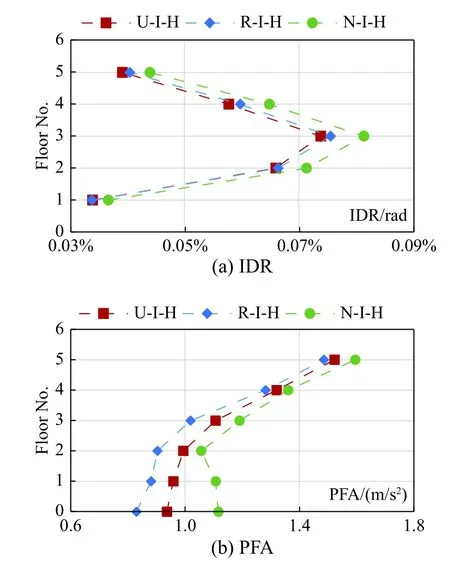
Fig. 7 Seismic responses of the base-isolated structure

Table 8 Peak seismic deformation of the LRBs /mm
2) The simulation results of the Rayleigh damping model are compared with those of the uniform damping model. Although their IDRs are relatively close (the maximum relative error is 3.45%), their PFAs are quite different (the maximum relative error is 11.38%).
During earthquakes, significant rigid-body motions occur in the superstructure of base-isolated structures. It is generally believed that rigid-body motion does not occur in a manner that results in damping behaviors, such as friction. However, in the Rayleigh damping model, the mass-proportional matrix introduces “spurious” damping forces[31]to the rigid-body motion, resulting in smaller LRB deformations and PFAs.
4.4 Environmental vibration analysis
With rapid urbanization and the popularity of rail transport, increased attention is being focused on subway-induced vibrations. Many studies have shown that subway-induced vibrations may severely affect buildings near the subway[33-35]. Therefore, the subway-induced vibration is used as an example of environmental vibration analysis in this study.
An accelerometer was used to collect the vertical acceleration induced by the subway. A flat and hard ground approximately 10 m away from the vibration source was selected as the collection location, and the sampling frequency was 256 Hz[36]. The collected data for the subway-induced vibrations are shown in Figure 8.The vibration has a peak acceleration of 0.177 m/s2,covers a wide frequency range, and provides large amplitudes from 50 Hz to 90 Hz. It was input along theZaxis of the structure.
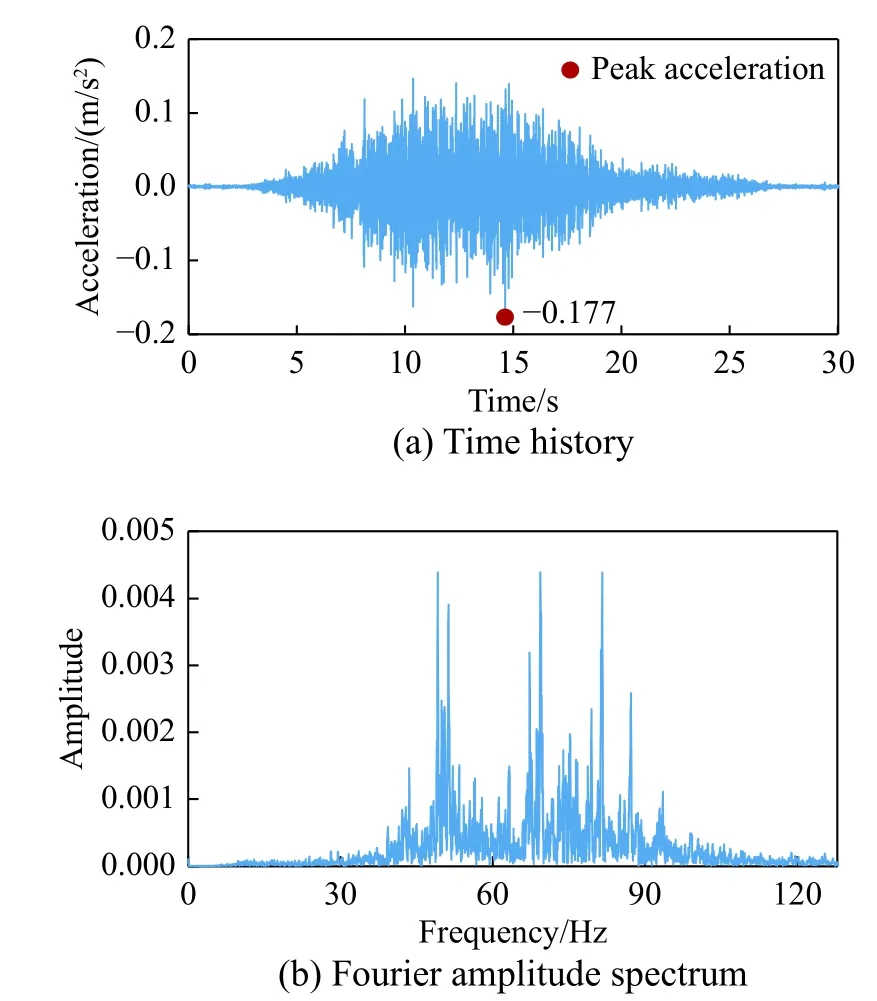
Fig. 8 Subway-induced environmental vibration[36]
The basic information of the investigated cases is presented in Table 9. As mentioned in the previous section, theExpressNewtonalgorithm[32]was used.The time step was 0.001 s, and the sampling frequency was 1000 Hz. The sampling frequency was more than 10 times the highest frequency of interest;hence, it could meet the requirements according to the Nyquist –Shannon sampling theorem. Before base isolation, the 1st and the 3rd vertical frequency were 6.18 Hz and 6.88 Hz, respectively. After base isolation, the 1st and the 3rd vertical frequency were 5.84 Hz and 6.71 Hz, respectively. From these modal analysis results, the lower bound of the frequency range for the uniform damping model and the reference frequencies for the Rayleigh damping model were determined.

Table 9 Environmental vibration analysis cases
The peak vertical accelerations (PVAs) of the top floor before and after base isolation are listed in Table 10. For all cases with different damping models,the PVA of the top floor after base isolation is lower than that before base isolation. Note that the effect of vertical vibration control is related to the specific structure and its base-isolation design. This study focuses on the influence of the damping models.Hence, the effect of the vertical stiffness of the LRBs on the vertical vibration control is not discussed in detail. For the structure in this case study, using LRBs can reduce both the horizontal seismic response and the vertical environmental vibration response.
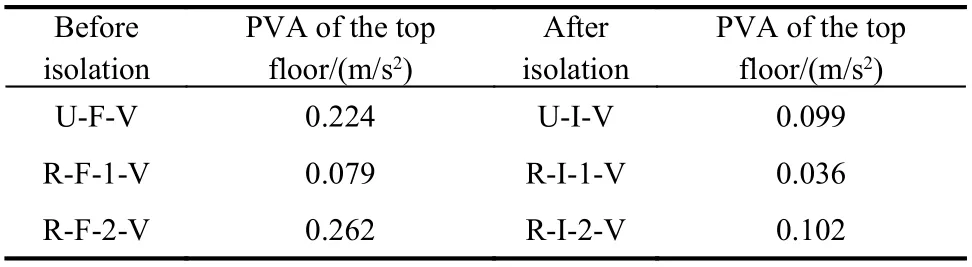
Table 10 Environmental vibration induced responses
Figure 9 shows the time history of the vertical acceleration response of the top floor after seismic isolation. The results are as follows.
1) The PVAs of U-I-V (Figure 9(a)) and R-I-2-V(Figure 9(c)) with a large frequency range are 0.099 m/s2and 0.102 m/s2, respectively. The relative error between R-I-2-V and U-I-V is 3.0%; the former is slightly larger.
2) The PVA of R-I-1-V (Figure 9(b)) is only 0.036 m/s2(relative error from U-I-V is -63.6%),which is significantly smaller.

Fig. 9 Vertical acceleration responses to subway-induced vibration
The Rayleigh damping model can only satisfy the target damping ratio at two specified frequencies(Figure 10). When the 1st and the 3rd natural frequencies were used as the reference frequencies,the Rayleigh damping model significantly overestimated the damping ratios of high-order modes(relative error 322%-653%) in the main input frequency band (50 Hz-90 Hz) and excessively suppressed the high-order modes excited by highfrequency environmental vibration. When the 1st natural frequency and 100 Hz were used as the reference frequencies, although the damping ratio between the reference frequencies was underestimated, the underestimation of the damping ratio in the main input frequency band (50 Hz-90 Hz)was small (relative error between -42.4% and -8.9%).Hence, the dynamic response was relatively reasonable.
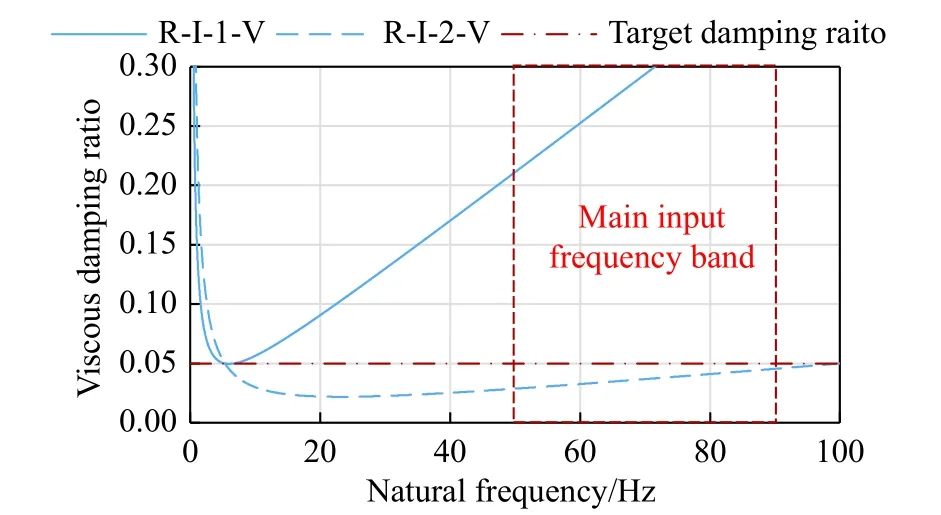
Fig. 10 Variation in Rayleigh damping with natural frequency
In addition to the above analysis, the vertical acceleration responses of the top floor after seismic isolation using different damping models were compared in the frequency domain. The one-third octave band spectrum for each case is presented in Figure 11. It can be observed that the responses of UI-V and R-I-2-V have relatively similar energy distributions. The response of R-I-1-V is significantly lower than those of the others. These results are consistent with the results obtained in the time domain.

Fig. 11 One-third octave band spectrum
5 Conclusion
This work presents a dynamic analysis of a baseisolated steel –concrete composite structure under earthquakes and environmental vibrations. The influence of the damping model selection (including the Rayleigh damping model and uniform damping model) on the analysis results is discussed. Based on the results, the following conclusions are drawn.
(1) For dynamic analyses under earthquakes and environmental vibrations, different frequency ranges are of concern under different excitations. Therefore,it is important to reasonably select and define a damping model according to specific excitations.
(2) For the Rayleigh damping model, different reference frequencies must be defined for seismic analysis and environmental vibration analysis. In addition, “ spurious” damping forces may be introduced owing to the rigid-body motion of the superstructure of the base-isolated structure, resulting in the underestimation of the deformation of LRBs and the PFAs of the superstructure.
(3) The uniform damping model is easier to use because only the upper and lower frequency bounds need to be considered. As a type of rate-independent damping model, its damping energy dissipation is essentially independent of the vibration frequency and it overcomes the theoretical defects of viscous damping models. Therefore, it has theoretical advantages in the dynamic analysis of structural design simultaneously governed by earthquakes and environmental vibrations.

