多孔介质梁的精细积分模型及有限元仿真

陈正轩， 陆 静，2， 潘 坤

（1.广西科技大学， 广西柳州 545006； 2.广西汽车零部件与整车技术重点实验室， 广西柳州 545006）

0 引言

多孔材料具有很多良好的特性， 在各领域内得到了广泛的应用。对多孔介质结构的振动特性进行研究分析，具有一定的理论和工程意义。在多孔介质材料的研究中，Biot 首先建立了分析多孔材料的经典理论[1]，在此基础上，学者对经典Biot 理论进行了简化，提出了更易理解应用的修正Biot 理论[2]。 结合Biot 理论，向宇等[3]建立了多孔介质矩形薄板的精细积分模型， 分析了多孔介质矩形薄板的的振动特性。 陆静等[4]将Boit 理论与经典弹性薄壳理论相结合， 建立了一种分析流体饱和多孔旋转薄壳振动的新模型。对于结构模型的求解，常用的有解析法[5]，解析求解方法仅能求解简单的模型， 随着有限元软件的发展，数值解法在结构模型的研究分析中多有出现，数值方法对于中低频段的问题求解较为精确， 对高频段问题的求解则具有一定的局限性。

本文以多孔介质梁为研究对象， 考虑多孔介质梁内部骨架和流体之间的耦合作用， 导出多孔介质梁的一阶常微分动力学控制方程， 利用精细积分方法对模型动力学控制方程进行求解， 与多孔介质梁的有限元仿真模型进行对比，验证了多孔介质梁精细积分模型的有效性。

1 多孔介质梁控制方程的建立

如图1 所示，梁的长、宽、高分别为a、l、h。 结构模型由多孔材料组成。

图1 多孔介质梁示意图

1.1 多孔介质梁的本构关系

基于 Biot 理论，不考虑y 方向的变形、内力和应力，得到多孔介质梁的本构关系[3]：

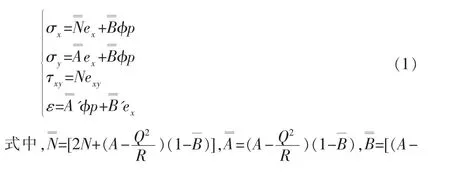
1.2 多孔介质梁固体骨架的几何方程

1.3 多孔介质梁骨架的运动方程

式中，ρ11—固体相对密度；ρ12—固体和流体的耦合密度。

1.4 多孔介质梁内部流体的运动方程和本构方程

记u^f， w^f为内部流体沿x，z 向的位移变量，uf，wf为内部流体形心沿x，z 向的位移变量。对于多孔介质梁内部流体，其运动方程：

2 多孔介质梁的控制方程

2.1 多孔介质梁一阶常微分控制方程

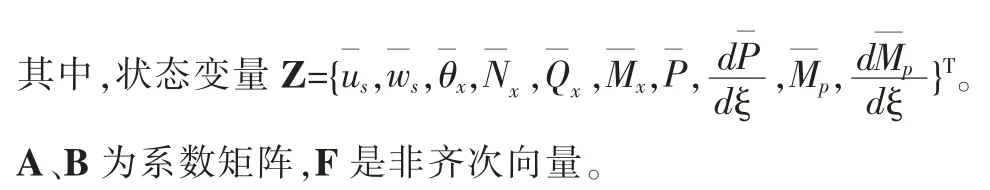
2.2 一阶常微分控制方程求解

图2 插值示意图

式中，方程个数为10M，但未知状态向量个数是为10（M+1），引入多孔介质梁模型的边界条件，代入式（35），即可解出全部的未知状态向量。

3 有限元仿真验证

为了验证本文建模和计算的正确性， 采用如表1 的主要参数，边界条件为两端简支，在Abaqus 中对多孔介质梁进行仿真， 与采用齐次扩容精细积分方法在同样参数条件下得到的多孔介质梁固有频率进行比较， 如表2所示，由表中数据可知，采用精细积分法所得到的多孔介质梁的前五阶固有频率和Abaqus 中仿真得到的结果较为接近，误差均小于10%，验证了本文方法的正确性。

表1 多孔介质梁的材料参数

表2 多孔介质梁固有频率的比较

4 结论

本文基于Biot 理论， 考虑了多孔介质梁的固体骨架和流体的耦合作用， 推导出了多孔介质梁的一阶常微分控制方程，用精细积分法对控制方程进行了求解，得到多孔介质梁的固有频率，与有限元仿真得到的结果比较，验证了此建模方法的正确性，并且，此建模方法对模型边界条件和频段范围有着较好的适用性。