LiCl-阴离子的光谱性质和跃迁性质*

郭芮 谭涵 袁沁玥 张庆 万明杰

(宜宾学院理学部，宜宾 644007)

采用多参考组态相互作用方法结合全电子基组计算了LiCl- 阴离子5 个电子态 (X2Σ+，A2∏，B2Σ+，32Σ+，22∏) 的电子结构.为了得到精确的光谱常数，计算中考虑了Davidson 修正、芯-价电子关联效应和自旋-轨道耦合效应.拟合得到各电子态的光谱常数、分子常数、自发辐射速率和自发辐射寿命.基态的光谱常数与实验值和其他理论值符合较好，同时报道了LiCl— 阴离子激发态的光谱常数以及其到基态的跃迁性质.计算结果表明A2∏ ↔ X2Σ+跃迁具有高对角分布的弗兰克-康登因子f00，第一激发态A2∏有较短的自发辐射寿命.构造A2∏ (ν′)↔ X2Σ+ (ν ′′)准循环跃迁进行激光冷却LiCl— 阴离子需要一束主激光和两束抽运激光.以上结果预测了激光冷却LiCl—阴离子是可行的.

1 引言

超冷分子在量子计算[1]、化学动力学[2]和控制化学[3]等领域有着广泛的应用.由于分子内部能级结构复杂，激光冷却分子存在巨大的挑战.Shuman等[4]于2010 年首次在实验上实现了分子的激光冷却.随后Zhelyazkova 等[5]于2014 年实现了YO分子的激光冷却，他们构造了一个闭合的三电子能级系统.至今为止，有很多关于激光冷却氯化物和锂化物的理论研究，如LiBe[6]，BeCl[7]，MgCl[8，9]，CaCl[10]，AlCl[11]和TlCl[12]分子.

2015 年，Yzombard 等[13]首次从理论上预测了双原子分子阴离子是适合激光冷却的候选体系.杨传路等[14，15]也分别讨论了激光冷却NH—和BH—阴离子的可能性.对两种阴离子而言，他们分别构造了11∏↔X1Σ+和12Σ+↔12∏准闭合的能级系统.近几年来，我们讨论了激光冷却OH—[16]，SH—[17]，KCl—[18]和SeH—[19]阴离子的可能性.LiCl—与KCl—阴离子的结构相似.以往的文献中很少有LiCl—阴离子和LiCl 分子关于势能性质方面的研究[20-23].1976 年，实验上第一次报道LiCl—阴离子的光谱[20]，并得到了其基态的平衡核间距.1986 年，Miller 等[21]报道了LiCl—的光电子谱，分辨率为80 cm—1(0.01 eV).实验得到了其基态的平衡核间距，离解能等光谱常数，同时得到了LiCl 分子电子亲合能为(0.593 ± 0.01) eV.1976 年，Jordan 和Luken[22]采用Hartree-Fock (HF)方法计算得到了LiCl—阴离子基态X2Σ+的势能曲线，他们得到基态的平衡核间距略大于2.12 Å.近年来，李松等[23]采用耦合簇方法计算了其基态的光谱常数和分子常数.2004 年，Weck 等[24]采用多参考单双激发组态相互作用 (MRSDCI) 方法计算得到了LiCl 分子X1Σ+和B1Σ+的势能曲线.两个电子态的势能曲线在8 Å左右发生避免交叉现象.2012 年，Kurosaki 和Yokoyama[25]采用MRSDCI 方法计算得到了LiCl 分子7 个Λ-S 态和13 个Ω 态的势能曲线，并拟合得到其基态的光谱常数.

从以往的研究中可以发现，只有极少数文献研究了LiCl—阴离子基态的光谱性质.本文将采用高精度的从头算方法计算LiCl—阴离子5 个较低的Λ-S 态和7 个Ω 态的电子结构，得到每个束缚态的光谱常数和分子常数.同时预测A2∏↔X2Σ+跃迁的弗兰克-康登因子，爱因斯坦系数和自发辐射寿命.最后讨论通过构造A2∏↔X2Σ+准循环跃迁能级进行激光冷却LiCl—阴离子的可能性.

2 计算细节

基于MOLPRO 2010 程序包[26]计算了LiCl—阴离子最低的3 个离解通道所对应的5 个电子态(X2Σ+，A2∏，B2Σ+，32Σ+，22∏) 的势能曲线.首先采用限制性的Hartree-Fock (HF) 方法得到LiCl—阴离子的初始能量;然后通过完全活动空间自洽场方法 (CASSCF)[27，28]产生多参考波函数;最后采用多参考组态相互作用方法 (MRCI)[29，30]得到所计算Λ-S 态的能量，考虑Davidson 修正 (+Q) 减小计算误差.在MRCI+Q 水平下通过Breit-Pauli哈密顿量[31]来考虑自旋-轨道耦合效应 (SOC).

由于程序的限制，必须把C∞V点群约化为C2V子群来计算LiCl—阴离子的电子结构.C2V群有4 个不可约表示 (a1，b1，b2，a2).在CASSCF 计算中，选择了8 个分子轨道 (4，2，2，0) 作为活动空间，包含了Li 2s2p 和Cl 的3s3p 壳层，可以写为CAS(9，8).Li 1s 和Cl 2s2p 选作闭壳层，保持双占据.其他的电子被冻结，不参与能量的计算.在MRCI+Q 计算中，Li 1s 和Cl 2s2p 用于考虑芯-价电子 (CV)关联效应，有17 个电子参与了相关能的计算.和K原子一样[32]，Li 原子采用了def2-AQZVPP-JKFI全电子基组[33]，Cl 原子采用了AWCVQZ-DK 全电子基组[34].

采用LEVVEL8.0 程序[35]求解径向薛定谔方程得到每个束缚态的平衡核间距 (Re)，离解能(De)，谐振频率 (ωe)，非谐振频率 (ωeχe)，转动常数(Be)和垂直跃迁能 (Te).同时计算出弗兰克-康登因子，爱因斯坦系数Aν′ν″(s—1) 和自发辐射寿命.爱因斯坦系数可以表示为

Λ′和Λ″分别表示高态和低态的电子角动量投影量子数，(2 —δ0，Λ′Λ″)/(2 —δ0，Λ′)表示简并因子，ΔEν′ν″表示振动能级之间的能量差，D(r)表示跃迁偶极矩，ψν′和ψν″分别表示高态和低态的振动波函数.

3 结果与讨论

3.1 Λ-S 态的势能曲线和光谱常数

在MRCI+Q 水平下计算得到了LiCl—阴离子X2Σ+，A2∏，B2Σ+，32Σ+和22∏态的势能曲线.图1描绘了5 个电子态的势能曲线.可以看到5 个电子态都是束缚态.Li 和Cl 原子的电子亲合能的实验值分别4984.86 cm—1[36]和29138.35 cm—1[37].可以得到基态X2Σ+对应最低的离解极限Li(2Sg)+Cl—(1Sg)，A2∏和B2Σ+电子态对应第二离解极限Li(2Pu) +Cl—(1Sg)，而32Σ+和22∏电子态对应第三离解极限Li—(1Sg)+Cl(2Pu).Λ-S 态之间的离解关系以及离解极限之间的能量差列于表1 中.从表1 可以看出，本文的计算的结果和已有实验值符合较好.同时本文计算了LiCl 分子的电子亲合能为0.4392 eV，比Miller 等[21]的实验值小0.153 eV.

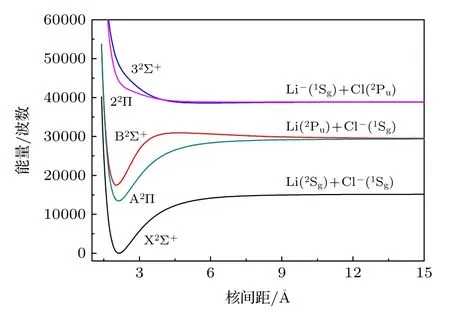
图1 X2Σ+，A2∏，B2Σ+，32Σ+和22∏电子态的势能曲线Fig.1.Potential energy curves of the X2Σ+，A2∏，B2Σ+，32Σ+ and 22∏ states.

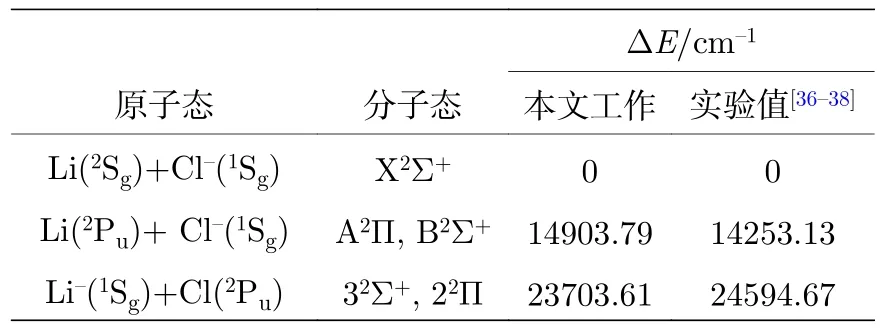
表1 LiCl—阴离子Λ-S 态的离解关系Table 1.Calculated dissociation relationships of the Λ-S states of LiCl— anion.

LiCl—阴离子5 个束缚态的光谱常数列在表2中.基态X2Σ+的平衡核间距为2.1352 Å，比最新实验值[21]大0.0112 Å，误差仅为0.5%，与最新理论值[23]相差仅0.0002 Å.相比与同主簇的KCl—阴离子，其基态的平衡核间距比KCl—阴离子约小25%[18].本文计算的谐振频率也仅比最新理论值小2.37 cm—1.基态在平衡核间距处的主要电子组态为1σ22σ23σ24σ21π45σ26σ22π47σ18σ03π0，权重为74.9%，其另外一个重要电子组态为1σ22σ23σ24σ21π45σ26σ22π47σ08σ13π0，权重为17.2%.基态有一个很深的势阱，其势阱深度达到了1.8556 eV.从表1 可以看出，本文计算的基态的光谱常数与已有实验值和理论值符合很好.第一激发态A2∏到基态的垂直跃迁能为13431.93 cm—1.其平衡核间距为2.1198 Å，比基态的平衡核间距小0.0154 Å.其在平衡核间距处的主要电子组态为1σ22σ23σ24σ21π45σ26σ22π47σ08σ03π1，权重为92.03%，A2∏↔X2Σ+跃迁源自7σ↔3π 跃迁.B2Σ+，32Σ+和22∏态在平衡核间距处的主要电子组态分别为1σ22σ23σ24σ21π45σ26σ22π47σ08σ13π0，1σ22σ23σ24σ21π45σ26σ12π47σ28σ03π0和 1σ22σ23σ24σ21π45σ26σ22π37σ28σ03π0，权重分别为74.5%，80.16%和80.16%，可以看出B2Σ+→X2Σ+，32Σ+→ X2Σ+和22∏ → X2Σ+跃迁分别来源于 7σ → 8σ，6σ → 7σ 和 3π → 7σ 跃迁.32Σ+和22∏态为弱束缚态，其谐振频率分别为30.19 cm—1和39.08 cm—1.其离解能仅为0.00353 eV 和0.0112 eV.从图1 中可以，看出两个态的势能曲线在约3.94 Å出现交叉.

表2 LiCl—阴离子Λ-S 态的光谱常数Table 2.Spectroscopic parameters of the Λ-S states of LiCl— anion.

3.2 振动能级和分子常数

基于精确的势能曲线，得到了J=0 时5 个Λ-S态 (X2Σ+，A2∏，B2Σ+，32Σ+和22∏) 的振动态，5 个态分别有65，90，31，30 和31 个振动态，限于篇幅，表3 中分别只列出了每个态前10 个振动态的振动能级Gν和转动常数Bν.2015 年，李松等[23]计算得到了6Li35Cl—阴离子基态的分子常数[23].本文中G0(X2Σ+)的计算结果和已有理论值的误差为1%，基态的其他结果与理论值[23]的误差均小于0.4%.可见本文的计算结果是可靠的.

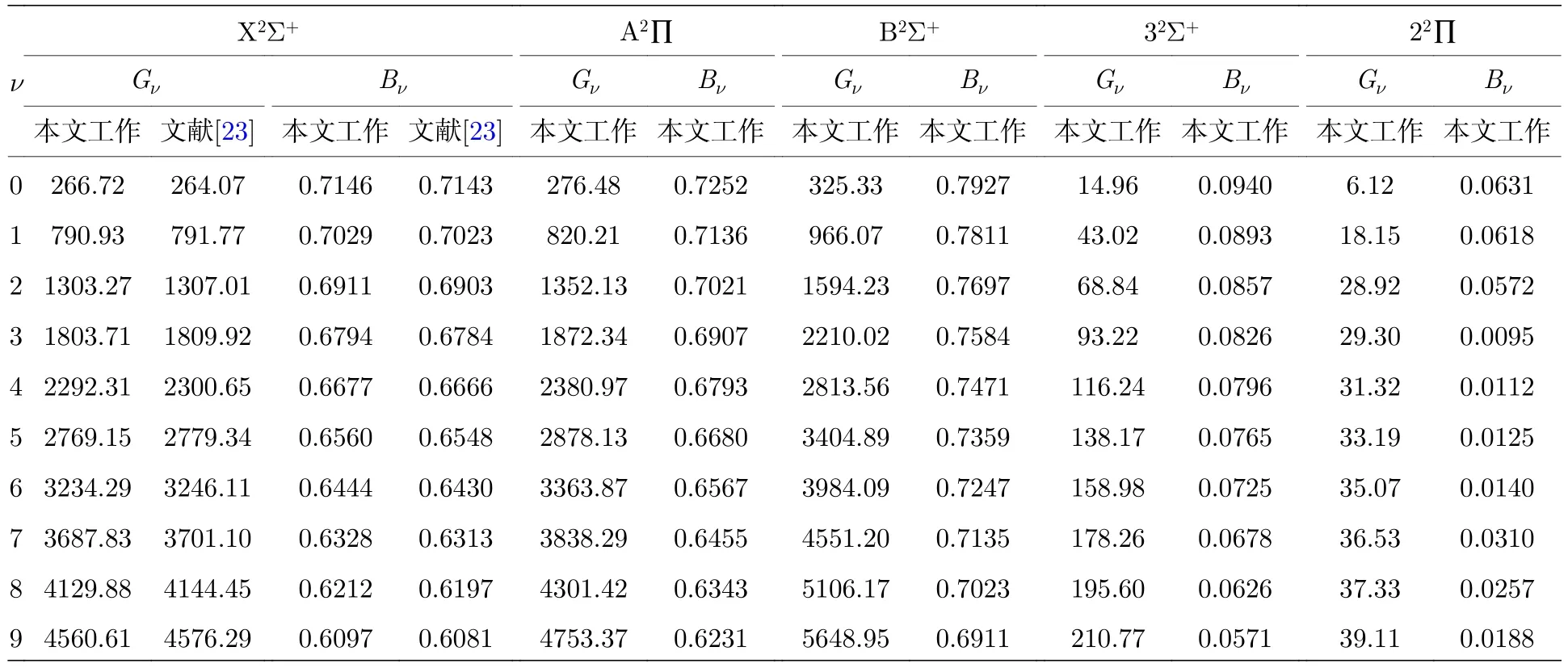
表3 X2Σ+，A2∏，B2Σ+，32Σ+和22∏态的振动能级和转动常数Table 3.Vibrational energy levels，rotational constants of the X2Σ+，A2∏，B2Σ+，32Σ+ and 22∏ states.

3.3 Ω 态的势能曲线和光谱常数

考虑SOC 效应后，Li 和Cl 原子的2P 原子态分裂为2P1/2和2P3/2.5 个Λ-S 态分裂为7 个Ω 态，包含了5 个1/2 和2 和3/2 态，分别对应5 个最低的离解极限，Ω 态之间的离解关系以及离解极限之间的能量差列于表4 中.Li (2P1/2)+Cl—(1S0)，Li(2P3/2)+Cl—(1S0)，Li—(1S0)+Cl (2P3/2)和Li—(1S0)+Cl(2P1/2)与最低离解极限Li—(1S0)+Cl(2P1/2) 之间的能量差分别为14252.77 cm—1，14253.50 cm—1，23415.41 cm—1和24288.48 cm—1，与实验值符合[36-38]的误差分别为4.37%，4.36%，3.06%和2.99%.计算得到Li (2P)和Cl (2P)的分裂值分别为0.26 cm—1和873.07 cm—1，仅比实验值[38]小0.075 cm—1和9.28 cm—1.从表4 可以看出本文的计算结果与实验值符合较好.

表4 LiCl—阴离子Ω 态的离解关系Table 4.Calculated dissociation relationships of the Ω states of LiCl— anion.

图2 Ω 态的势能曲线Fig.2.Potential energy curves of the Ω states.

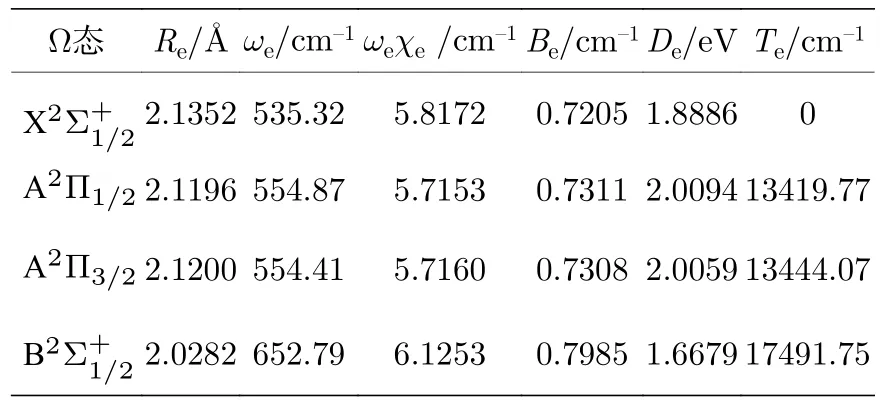
表5 LiCl—阴离子Ω 态的光谱常数Table 5.Spectroscopic parameters of the Ω states of LiCl— anion at icMRCI+Q level.

本文计算了电子态之间的SO 矩阵元，通过其大小来判断SOC 相互作用的强弱，表6 中列出了所计算电子态之间可能的16 个SO 矩阵元，其中表示A 和B 态之间的SO 矩阵元.SO矩阵元随核间距变化的曲线绘制在图3 中.SO1和SO2表示X2Σ+和A2∏的两个分量之间的SO矩阵元，故两者大小相等，同样SO3=SO4，SO5=SO6，SO7=SO8，SO9=SO10，SO11=SO12，SO14=SO15.图3 中可以看到，22∏的两个分量之间以及22∏与32Σ+之间的矩阵元达到了近300 cm—1，SOC效应对22∏态的影响较大，而其他的SO 矩阵元非常小，说明SOC 效应对X2Σ+，A2∏，B2Σ+电子态的影响很小，基本可以忽略.因此本文在自旋无关水平下研究了LiCl—阴离子的跃迁性质及激光冷却的可能性.

表6 LiCl—阴离子的自旋-轨道矩阵元Table 6.Notation of spin-orbit matrix element.

图3 LiCl—阴离子的自旋-轨道矩阵元.SOi 的表示见表5Fig.3.Spin-orbit matrix elements of the of the LiCl— anion.The explanations of the SOi symbols are presented in Table 6.

3.4 偶极矩，跃迁偶极矩，弗朗克-康登因子，爱因斯坦系数

X2Σ+，A2∏，B2Σ+，32Σ+和22∏态的电偶极矩以及激发态到基态跃迁的跃迁偶极矩随核间距变化的曲线分别描绘于图4(a)和图4(b)中.基态X2Σ+平衡核间距处的电偶极矩达到了2.268 a.u，比SrF 分子 (1.378 a.u) 和KCl—阴离子 (1.212 a.u)要大很多，所以其极性很强.也说明激光冷却LiCl—阴离子能满足电偶极矩较大的条件.由于其是一个强极性的分子离子，故其电子态的电偶极矩在无穷远处不为零，从图4(a)中可以看出，当核间距大于4 Å时，电偶极矩随核间距的增加基本成线性增大的关系.由于X2Σ+，A2∏和B2Σ+态来源于Li+Cl—，故三个态的电偶极矩有同样的变化趋势，32Σ+和22∏态来源于Li—+Cl，故这两个态的电偶极矩趋近于另一极限.

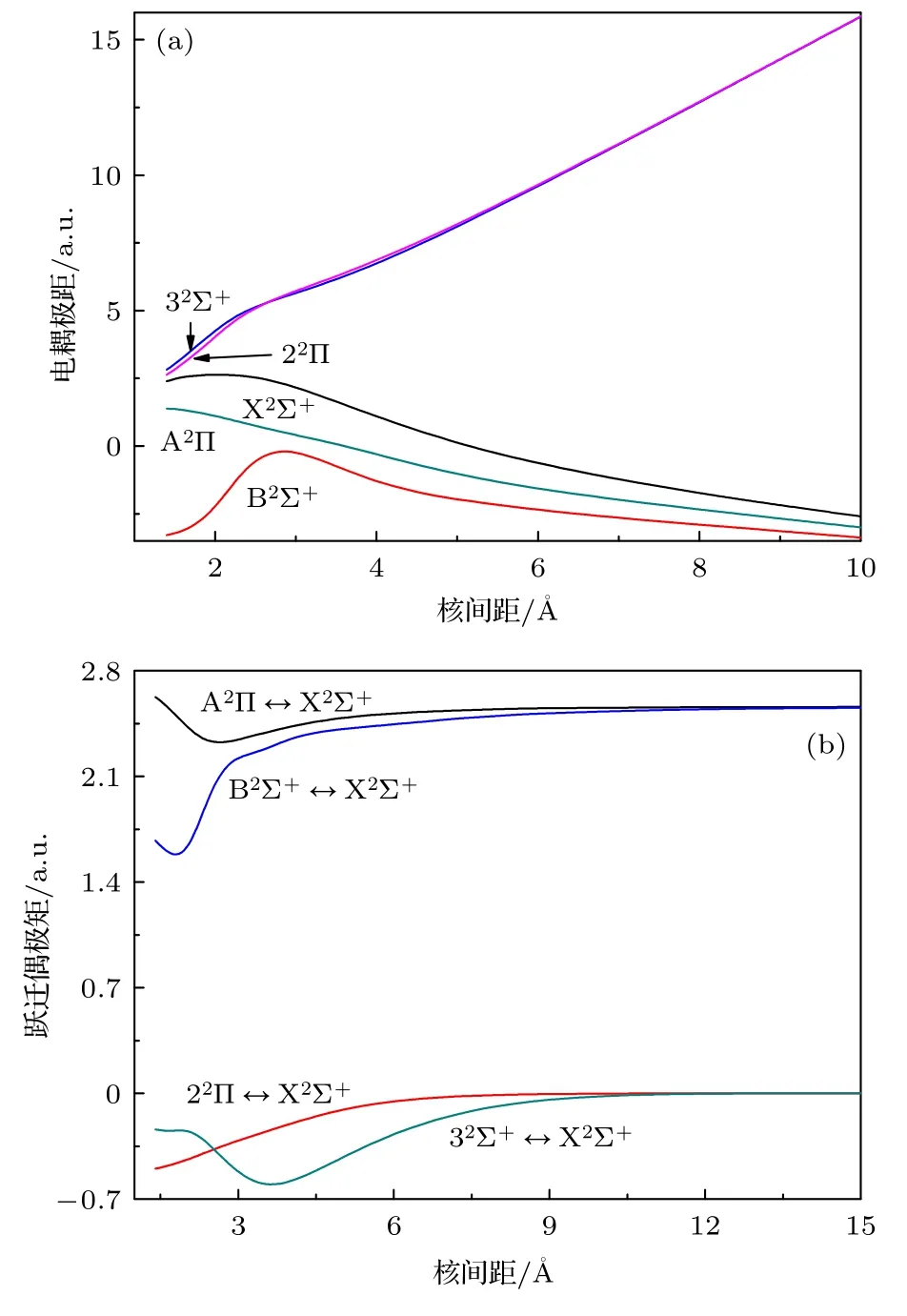
图4 (a) Λ-S 态的电偶极矩;(b) Λ-S 态的跃迁偶极矩Fig.4.(a) The permanent dipole moments of the Λ-states;(b) the transition dipole moments of the Λ-states.

由于A2∏和B2Σ+态具有同样的离解极限，A2∏↔X2Σ+和B2Σ+↔X2Σ+跃迁在核间距无穷远处源自于Li 原子2Sg到2Pu的跃迁.它们的跃迁偶极矩随着核间距的增大趋于同一值2.561 a.u.在平衡核间距处，A2∏↔X2Σ+和B2Σ+↔X2Σ+跃迁有很大的跃迁偶极矩，分别达到了2.393 a.u和1.712 a.u，22∏↔X2Σ+和32Σ+↔X2Σ+跃迁比A2∏↔X2Σ+和B2Σ+↔X2Σ+跃迁的跃迁强度弱很多.

本文计算了A2∏↔X2Σ+和B2Σ+↔X2Σ+跃迁的弗兰克-康登因子fν'ν''，爱因斯坦系数和自发辐射寿命，计算结果见表7.A2∏↔X2Σ+跃迁具有高对角分布的弗朗克-康登因子，而B2Σ+↔X2Σ+跃迁对角分布的弗朗克-康登因子比较小.两种跃迁都有较大的爱因斯坦系数，当ν'=0 时，两种跃迁总的爱因斯坦系数分别为2.821×107s—1和2.858×107s—1，A2∏和B2Σ+态的自发辐射寿命分别为35.45 ns 和34.99 ns.当ν'=1 时，两种跃迁总的爱因斯坦系数分别为2.823×107 s—1和3.03×107s—1，自发辐射寿命分别为35.43 ns 和33.0 ns.

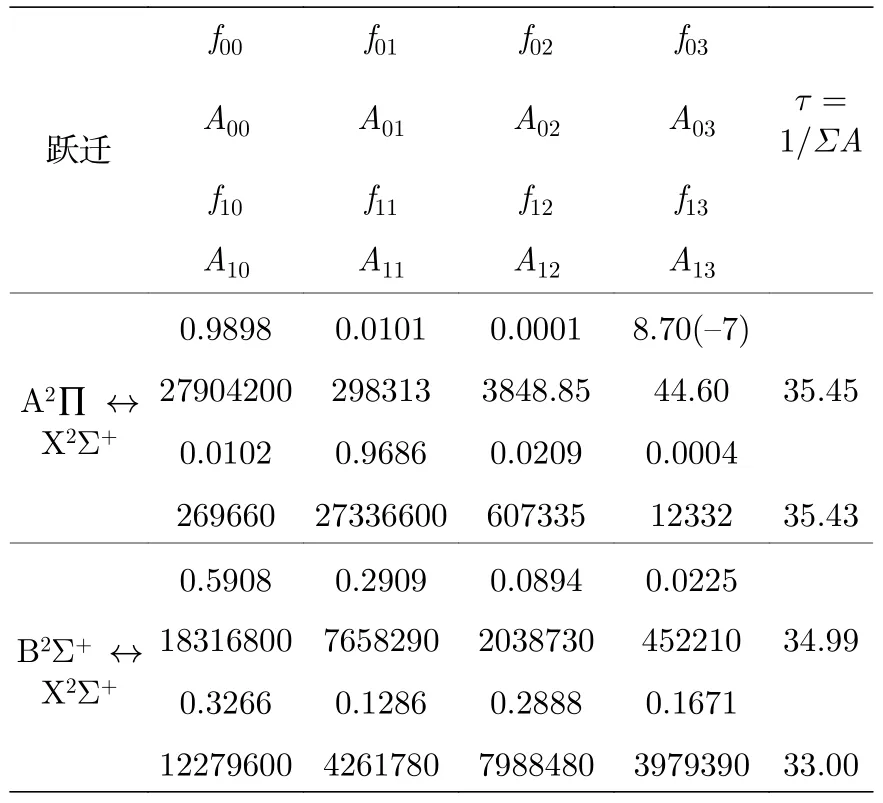
表7 A2∏ ↔ X2Σ+和B2Σ+ ↔ X2Σ+跃迁的弗兰克-康登因子fν'ν''，爱因斯坦系数Aν'ν''和自发辐射寿命 (单位:ns)Table 7.Franck-Condon Factors fν'ν''，Einstein coefficients Aν'ν''，and radiative lifetimes τ of the A2∏ ↔ X2Σ+ and B2Σ+ ↔ X2Σ+ transitions of LiCl— anion(in ns).

3.5 激光冷却LiCl-阴离子的可行性

X2Σ+，A2∏和B2Σ+的势能曲线没有交叉和避免交叉，SOC 效应对着3 个态的势能曲线和跃迁性质的影响也不明显，本文将在自旋无关水平下讨论激光冷却LiCl—阴离子的可能性.

A2∏↔X2Σ+跃迁的弗朗克-康登因子f00=0.9898，比SrF 分子和CaH 分子的f00略大 [f00(SrF)=0.98[4]，f00(CaH)=0.985[39]]，也 比同主簇KCl—阴离子的f00大很多 (f00=0.8816)[18]，说明激光冷却LiCl—阴离子具有足够大的f00.另一方面，A2∏态的自发辐射寿命只有35.45 ns，足以快速的激光冷却LiCl—阴离子.

振动分支比Rν'ν''比fν'ν''能更加准确的描述循环过程中的光子损失.振动分支比Rν'ν''可以表示为

A2∏↔X2Σ+跃迁的对角项分支比R00和R11分别为0.9893 和0.9685，非对角项分支比分别为:R01=0.0106，R02=1.36×10—4，R03=1.58×10—6，R10=0.0096，R12=0.0215，R13=4.37×10—4，可以得到R00，R01和R02的和非常接近1，说明A2∏(ν′)↔X2Σ+(v′′)跃迁是一个准循环跃迁能级系统.其冷却途径见图5.红线表示泵浦激光其中主激光波长λ00为744.10 nm，为了提高冷却效率，增加了两束抽运激光，其波长分别为λ10=774.30 nm 和λ21=772.42 nm.激光冷却LiCl—阴离子所需激光波长要小于冷却KCl—阴离子所需波长[18].蓝线表示从A2∏自发辐射到基态的振动分支比.R03+的表示ν″≥ 3 的所有分支比之和，计算得到R03+＜ 1.60×10—6，则理论上至少能散射6×105个光子.故可以构造A2∏(ν')↔X2Σ+(v′′)准闭合能级系统进行激光冷却LiCl—阴离子.

图5 驱动A2∏ ↔ X2Σ+跃迁进行激光冷却的途径Fig.5.Proposed laser cooling scheme via A2∏ ↔ X2Σ+ transition.

虽然B2Σ+态的自发辐射寿命足够小，但由于B2Σ+↔X2Σ+跃迁的弗兰克-康登因子太小，f00=0.5908，故没有考虑构建B2Σ+↔X2Σ+跃迁进行激光冷却LiCl—阴离子.

4 结论

本文采用MRCI+Q 方法计算了LiCl—阴离子X2Σ+，A2Π，B2Σ+，32Σ+和22Π 电子态的势能曲线，电偶极矩和跃迁偶极矩.计算过程中考虑了CV 关联和SOC 效应.计算结果表明5 个Λ-S 态和7 个Ω 态都是束缚态.通过求解径向薛定谔方程得到束缚态的光谱常数和分子常数.基态的光谱常数与分子常数与已有实验值和理论值符合较好.得到了A2∏↔X2Σ+和B2Σ+↔X2Σ+跃迁的弗兰克-康登因子，爱因斯坦系数和自发辐射寿命.本文报道了LiCl—阴离子激发态的光谱常数，分子常数和跃迁性质.通过分析SO 矩阵可以得到SOC 效应对X2Σ+，B2Σ+，A2∏的光谱常数和A2∏↔X2Σ+和B2Σ+↔X2Σ+跃迁的跃迁性质影响很小，可以忽略.A2∏(v′)↔X2Σ+(v′′)跃迁具有高对角分布的弗兰克-康登因子以及较小的自发辐射寿命，同时得到了激光冷却所LiCl—阴离子需的激光波长.在自旋无关水平下预测LiCl—阴离子是适合激光冷却的候选离子.