超临界二氧化碳类液-类气区边界线数值分析*

孙辉 刘婧楠† 章立新 杨其国 高明

1) (上海理工大学能源与动力工程学院，上海 200093)

2) (上海市动力工程多相流动与传热重点实验室，上海 200093)

超临界二氧化碳(S-CO2)因在萃取、沉淀、热力循环及化学反应等方面有着十分广阔的应用前景，逐渐成为学术界的重要研究课题.由于在近临界区，可以观察到随温度或压力变化出现大量的物性异变现象，使得各国学者对流体临界点附近区域的研究产生了浓厚兴趣.随着分子动力学模拟技术的快速发展，该技术可辅助传统实验方法用于研究近临界流体的相关物性.为确定S-CO2 在近临界区Widom 线范围及类液-类气区的分子结构特征，本文通过分子动力学模拟技术结合聚类分析，研究了温度和压力范围分别在300—350 K和5.5—18.5 MPa 下，CO2 密度时间序列变异系数及偏度同Widom 线和类液-类气区间的关系.结果表明:S-CO2在近临界区Widom 线的确定可通过连接密度时间序列曲线变异系数极大值点来确定，Widom 线沿着临界点开始延伸直到350 K 时停止;S-CO2 类液区和类气区的分子分布结构可以用数密度分布的偏度来区分，偏度在类气态时为正值，在类液态时为负值，而在Widom 线上达到最大值.

1 引言

自19 世纪Charles Cagniard de Tour 发现超临界流体以来，超临界流体已被广泛研究并应用于不同行业中.由于超临界二氧化碳(supercritical carbon dioxide，S-CO2)在萃取、沉淀、热力循环及化学反应等方面中有着十分广阔的应用前景，逐渐成为学术界重要研究课题[1，2].通常，流体超临界区被定义为温度和压力均高于其临界点的区域，流体物性随着等温线和等压线连续变化，但不会伴随着液气相变.然而，近年来学术界对流体临界点附近区域的研究产生了浓厚兴趣，因为在近临界区，可以观察到随温度或压力变化出现大量的物性异变现象(即所谓的临界行为)[3].

现有研究指出，临界点附近二氧化碳的物性变化将显著降低循环中的压缩功，同时对涡轮机设计的影响不可忽略[4].Clarke 等[5]在研究中就强调物性，如比热容和密度等的微小变化会显著影响热交换器的设计和性能.众所周知，许多热力学函数，包括比热容、等温压缩和热膨胀等系数，在临界点附近出现最大值.有学者指出不同参数的最大值在(P，T)平面上彼此相距不远，并引入了单条超临界区最大值线，称其为Widom 线[6]，该术语最初仅用于表示相关长度的异常.在压力-温度空间，不同的物性对应着不同的Widom 线，所以这些Widom 线最终形成一个楔形的Widom 区域，指向临界点，标志着一些物性(如压缩性、比热容、密度、热膨胀性、声速)表现出异常行为的区域.关于超临界流体Widom 区，已经开展了大量的研究.Nishikawa 等[7-9]就对超临界流体进行了系列小角度X 光散射实验，并指出相关长度和密度波动沿着气液共存曲线延伸到超临界区域形成了一个“脊”线，该“脊”线被定义为密度波动在等温线上达到最大波动尺度的轨迹;Simeoni 等[10]通过非弹性X 光散射和分子动力学模拟，揭示了氩气在超临界区可被分为类液和类气两个区域;Brazhkin等[11]对氩和氖的热膨胀系数、可压缩性和密度涨落进行了分子动力学模拟，指出单一的Widom 线终止于偏离临界温度10%的超临界区;Sedunov[12]利用分子动力学模拟技术提出一种能量平均密度团簇数的研究方法，分析了S-CO2中类气体和类液体之间的软结构转变机理;Bolmatov 等[13]通过衍射测量，结合分子模拟技术，解释了超临界流体中的结构交叉现象，并发现了温度-压力图上的新热力学边界，即Frenkel 线，该线与Widom 线的区别是，前者与超临界流体中基本微观结构和动力学特征的交叉相关，而后者由热力学响应函数的最大值的轨迹定义;Mareev 等[14，15]就近临界流体非线性折射率行为进行了研究，表示团簇的形成是导致非线性折射率产生的主要原因;在我们之前的研究中，也曾对S-CO2在Widom 线对应的温度压力范围内的折射率进行了预测，并对其光学异变进行了微观解释[16，17].综上所述，Widom 线将流体超临界区分成类液区和类气区，随着分子模拟技术的快速发展，可辅助传统实验方法用于研究近临界流体的物性异变现象.

分子动力学模拟常用于模拟气体、液体和固体分子的性质，以高精度还原真实的分子微观状态.本文以分子动力学为基础，用计算机模拟了粒子间相互作用的时间演化过程，所有的分子模拟均是在LAMMPS 开源软件下进行计算的.值得注意的是，在Widom 线所处的温度压力区域内，正常液体和气体的一些已建立的流量和热交换计算方法不能使用，因为它们不能处理与这些异变行为有关的突然变化[18].对涉及超临界状态的流动(包括泄漏)和换热的问题，为了避免在Widom 线所处的温度压力区域内使用常规计算方法，了解这一异变区域的位置是至关重要的，可以提醒工艺设计人员应注意到异变区域出现的压力-温度范围[19].因此本文利用分子动力学模拟方法，通过对密度时序曲线、分子聚类等特征进行分析，揭示了S-CO2Widom线对应的温度压力范围、类液-类气区结构特征及其判定方法，能够辅助工艺设计人员或科研人员寻找异变区域大致位置范围及对类液-类气结构进行判定.

2 物理模型及模拟细节

图1 为物理模型示意图.模拟体系是各边长为10 nm 的立方体盒子，内有1000 个CO2分子.系统沿着x，y，z三个方向均采用周期性边界条件.模拟过程中对整个系统施加NPT 系综，温度和压力的控制采用Nose-Hoover 恒温器[20]，并采用Kamberaj 等[21]描述的算法动态更新坐标和速度.设定时间步长为1 fs，将运动方程和velocity-Verlet算法相结合，在各时间步长下更新原子的位置和速度.在每个温度和压力下，共运行1000 万时间步，前500 万时间步使系统达到平衡状态，后500 万时间步的结果每100 fs 输出一次.对于每一个分子，分子动力学模拟只计算以该分子为中心，以4σ为半径的球内所有粒子与它的相互作用，从而使计算更加精确，本文潜在的截断值参考Aimoli 等在文献[22]中的数值，设为4σ(σ为尺寸参数).

图1 物理模型Fig.1.Physical model.

S-CO2的临界温度(Tc)为304.13 K，临界压力(Pc)为7.377 Mpa[23].如图2 所示，本文模拟工况温度范围在0.98Tc—1.15Tc，压力范围在0.75Pc—2.1Pc(对于温度340 K 和350 K 两种工况，压力范围分别为1.01Pc—2.5Pc，1.15Pc—2.64Pc).本文所作分子动力学模拟采用标准的12-6 Lennard-Jones 势能模型，表达式为：

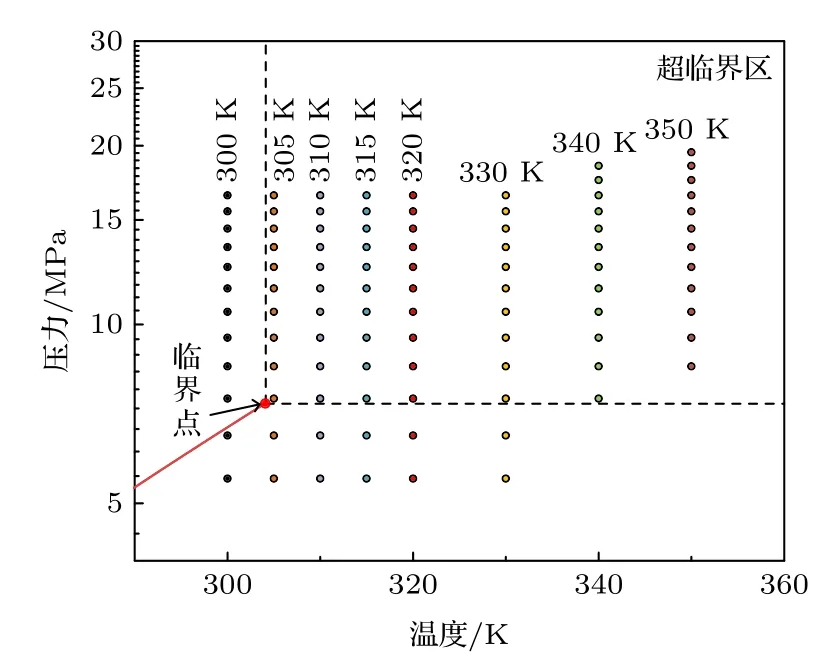
图2 模拟参数范围Fig.2.Range of simulation parameters.

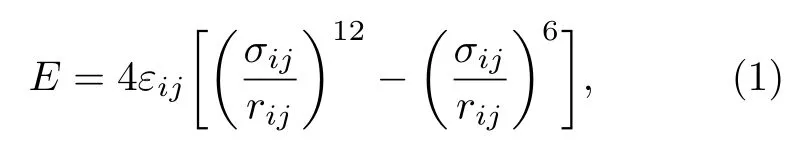
式中，E和rij分别表示原子i和原子j之间的势能和距离;εij为势能阱深度，表明粒子间相互作用的强弱;σij表示粒子间相互作用势为0 的有限距离，与原子直径有关.本文力场模型选用EPM2 刚性三位点模型，该模型已被学术界广泛用于S-CO2分子动力学模拟中，并有学者经过综合比较，认为该模型相较于其他模型有着更高的适用性和准确性[22，24，25].表1 中列出了该模型的参数，其中r0指的是CO2中的C—O 化学键的长度.对于异对原子的相互作用参数，可用洛伦兹-贝特洛组合(Lorentz-Berthelot combining rules)规则计算[26]，具体为：

表1 EPM2 力场[27]模型参数Table 1.Force field model parameter.

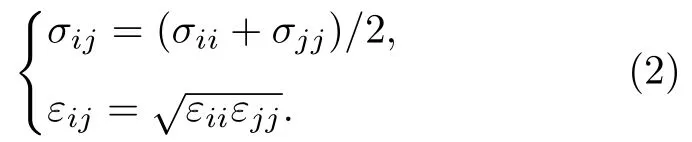
对于库仑成对相互作用，采用基于原子的部分电荷模型，并使用(3)式计算库仑相互作用:

其中C是能量转换常数，qi和qj分别表示两原子电荷，而ε是真空介电常数.

3 结果与讨论

尽管超临界流体的物性随温度和压力的变化而连续变化，但在临界点附近出现大多数热力学特性的异变行为.在临界点附近，可以观察到由吉布斯热力学势的二阶导数确定的物性参数的临界行为，如压缩系数、热膨胀系数和定压比热等会随着压力的变化出现极值.以定压比热(Cp)为例，通过NIST 数据库[28]计算了CO2在一段温度范围内的定压比热，结果如图3 所示.S-CO2在近临界温度开始，随着压力的增加，定压比热会出现极值点，且随着温度的增加，极值点所对应的压力也会变大.这种现象会随着温度远离临界温度而逐渐消失.实际上，对于其他的物性参数，也会出现类似的情况.在P-T图中连接这些极值点，就会出现不同的Widom 线，构成前文所述的Widom 楔形三角区.

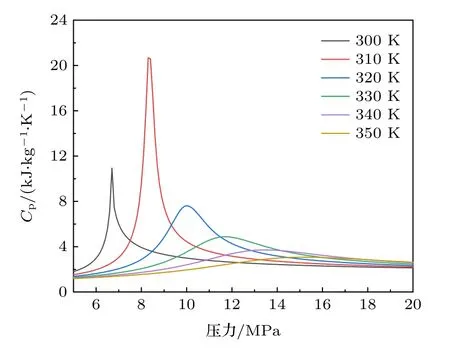
图3 不同温度下CO2 的定压比热Fig.3.Specific heat of CO2 under constant pressure at different temperatures.

通过分子动力学模拟可以发现，密度的时间序列曲线波动幅度和上述极值点出现的位置非常接近.以温度310 K 为例，分子模拟在不同压力下的密度时间序列曲线如图4 所示，可知Cp值和密度时间序列曲线波动幅度均在8.5 MPa 时表现出最大值.鉴于时间序列曲线波动幅度与物性异变极大值发生的压力范围一致，因此考虑，可通过密度时间序列曲线振幅，分析Widom 线对应的温度压力范围，并界定类液-类气区间.

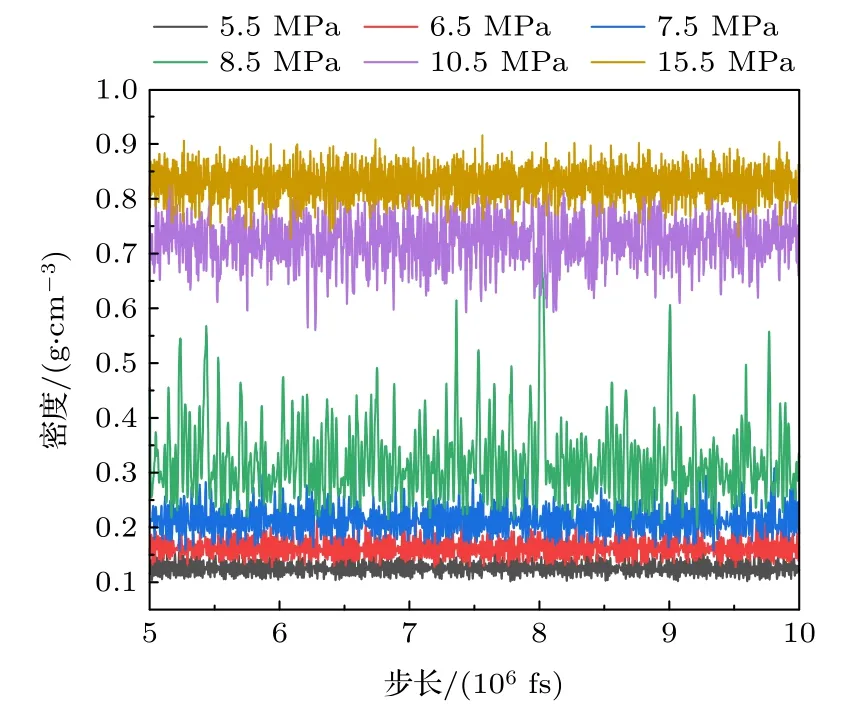
图4 密度时间序列曲线Fig.4.Density time series curve.

3.1 S-CO2 的Widom 线确定

在表示一组数据离散程度的各项指标中，实验标准差(Sx)是最重要且最常用的，表达式如下:

式中，Xi表示第i个时间下的密度值;n表示时间序列对应的密度样本总数;表示密度平均数.表2是本文模拟不同温度和压力工况下的密度时间序列曲线标准差，可以看出在不同温度下，标准差随着压力的变化会出现最大值，标准差越大，则表示曲线波动程度越大.

然而，当温度较低时，压力的线性变化将会带来密度的非线性跳跃增加，各组数据的测量尺度差异太大，直接比较标准差是不适合的.为消除量级的影响，引入变异系数Cv，表示标准差Sx同平均数之间的比值:

变异系数没有量纲，其值越大，表示变量的离散程度越大，变量的均衡性越差.图5 表示了温度和压力分别在300—350 K 和5.5—19.5 MPa 范围内S-CO2密度时间序列的变异系数.可以看出，随着温度的增加，变异系数极值点对应的压力逐渐变大，且与NIST 计算的物性参数极大值对应压力一致，在温度为350 K 时，这种现象逐渐消失.

图5 密度时间序列曲线变异系数Fig.5.Coefficient of variation of density time series curve.

连接变异系数的极值点，可以在P-T图中确定出一条Widom 线，如图6 所示.

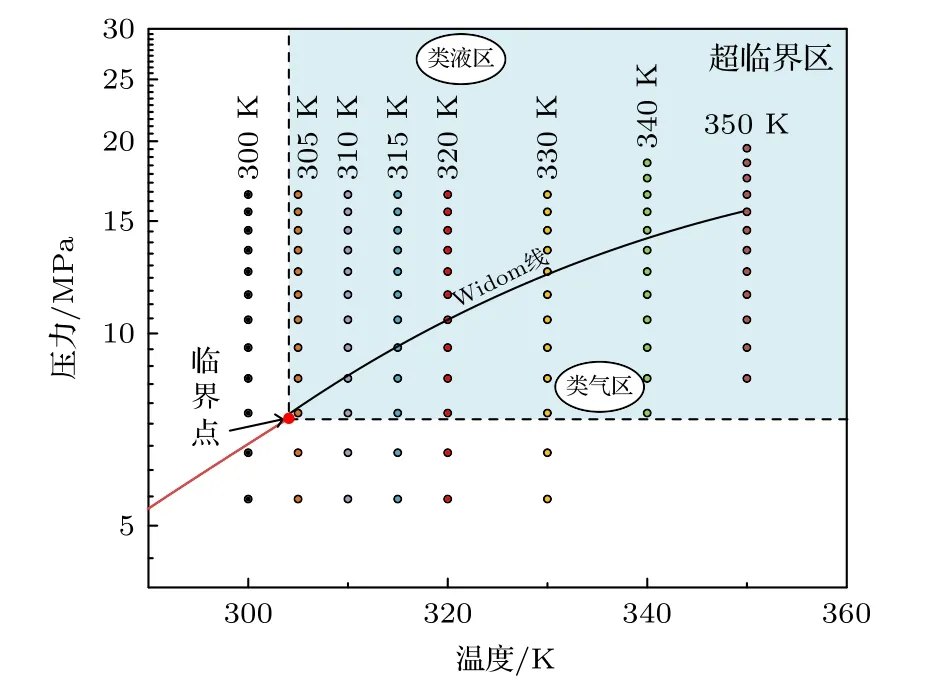
图6 Widom 线的确定Fig.6.Determination of Widom Line.

在Widom 线的上半部分称为类液区，在Widom线的下半部分称为类气区.本文同时利用NIST 对相同工况范围内的S-CO2定容比热、等温压缩系数、体积膨胀系数进行了计算，将极大值进行连线后发现，在310 K 之前，NIST 计算的3 种参数极大值对应的压力与本文变异系数预测值一致，310—350 K 范围内接近.从而进一步证明了本文方法的有效性.

Widom 线像是亚临界区气液边界线的延长线，终止于350 K.但是，仅通过变异系数无法判断类液区和类气区的特征，因此考虑引入了偏度系数.

3.2 S-CO2 类液-类气区特征

偏度系数k是统计数据分布偏斜方向和程度的度量[29]，表示曲线相对于均值不对称程度的特征数，表达式为：

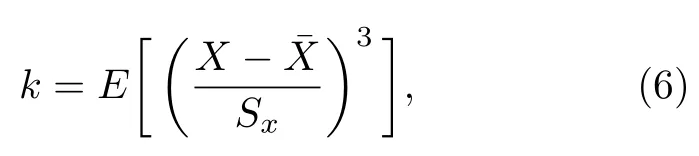
其中E表示期望值.如果数据对称，偏度等于0;若偏度大于0，则表示均值右边的数据更为分散，表明数据右偏;若偏度小于0，则表示数据左偏.表3 列出了本文模拟工况下的偏度值.

对照变异系数来看，偏度和类液-类气的区分有着很大的关联.如图5 中，当温度为305 K 时，变异系数极大值对应的压力为7.5 MPa，在图6中，当压力高于此数值时，均表现为类液区，而在表3 中此区域对应的偏度均为负值.因此从总体看，当压力小于变异系数极大值对应的压力时，偏度值为正数，即右偏，相对于正态分布密度曲线，其峰值靠左，此时小于均值的数据比大于均值的数据多，总体密度偏小，此时流体偏气态.当压力大于变异系数极大值对应的压力时，偏度值为负数，即左偏，相对于正态分布密度曲线，其峰值靠右，此时大于均值的数据比小于均值的数据多，总体密度偏大，流体偏液态.

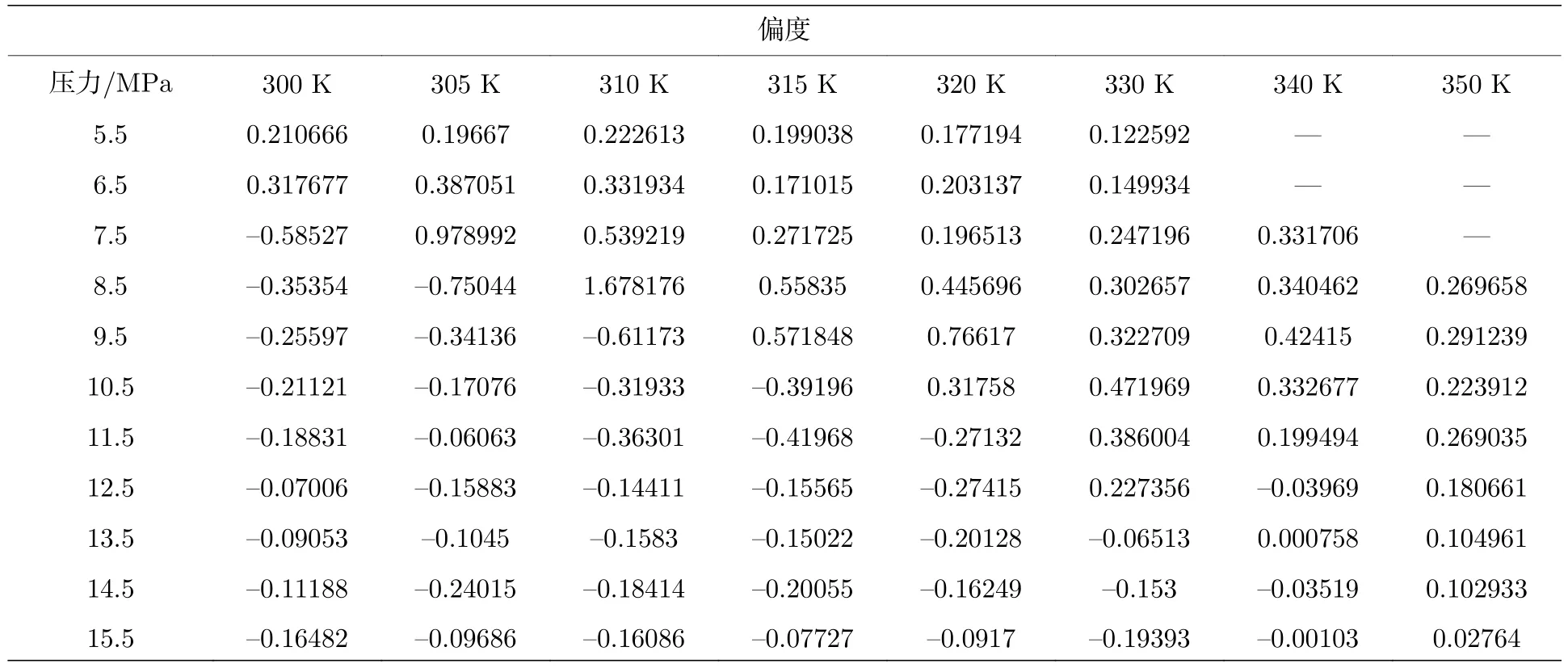
表3 密度时间序列曲线偏度Table 3.Skewness of density time series curve.

图7 给出了温度分别为305，330，350 K 下不同压力处的偏度，可以看出，当温度为350 K 时，偏度的正负区分消失.

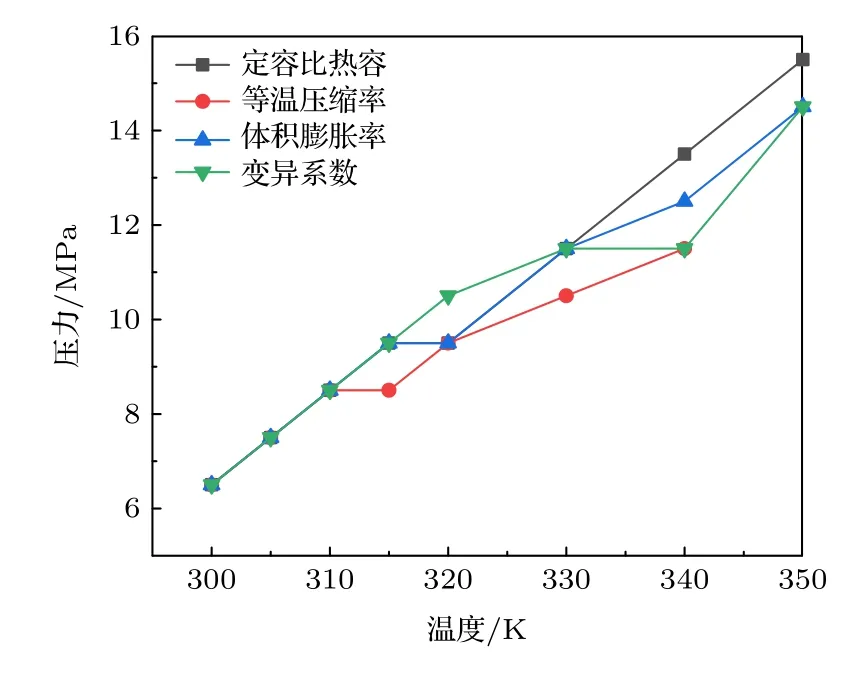
图7 NIST 计算结果同变异系数比较Fig.7.NIST results were compared with coefficient of variation.

利用Ovito 软件可以直观地展示分子在不同压力下的聚类情况，设定分子间截断距离为3.5 Å(一个CO2分子的大小约为3.2 Å)，在此范围内的所有分子称为一个簇，用相同颜色表示.图8 给出了温度为305 K，压力分别为6.5，7.5，15.5 MPa 下分子聚类示意图，并在稳定后对20 个时间步平均得到了团簇个数(其余温度下的聚类情况与之类似).图9 为分子聚类在 P-T 图中的表示.

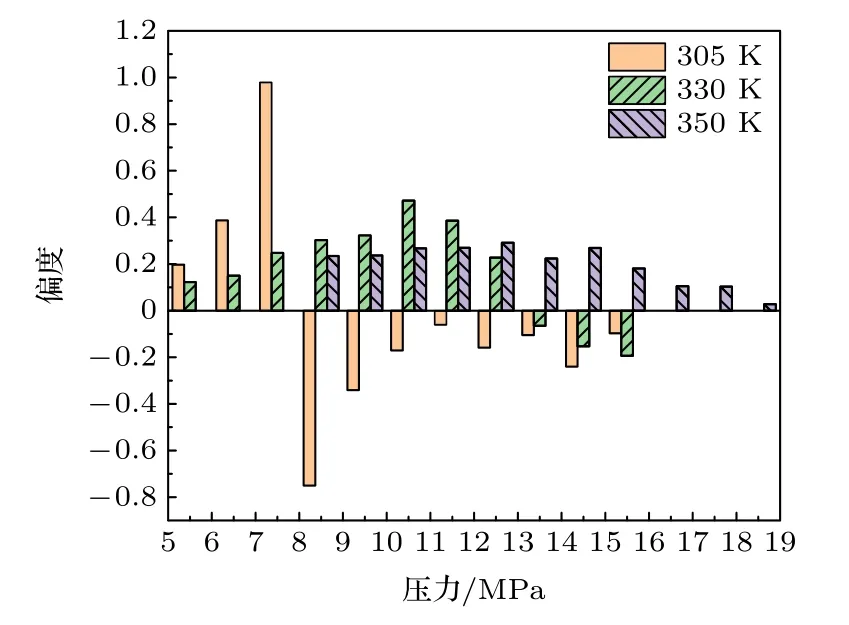
图8 不同压力下偏度Fig.8.Different pressure of skewness.

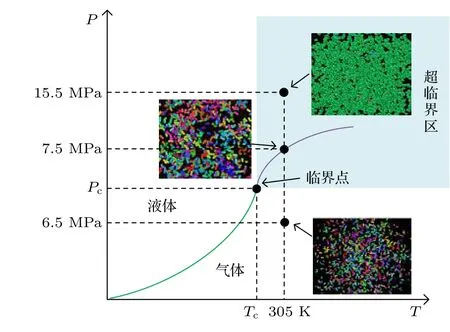
图9 分子聚类在P-T 图中的表示Fig.9.Representation of molecular clustering in a P-T plot.

结合偏度可知，当压力为6.5 MPa 时(虚线最低点)，此时偏度为正值，分子共产生641 个团簇，其中最大团簇包含68 个CO2分子，分子间空隙较大，表现为类气体特征;当压力为7.5 MPa 时(虚线中间点)，偏度达到最大值，分子团簇数明显减少，仅包含493 个团簇，最大团簇包含130 个CO2分子，密度分布的不对称性增加，但分子间的空隙依旧较大，近似于类气体状态，但实际上正处于类液到类气的过渡状态，即伪沸腾状态;当压力为15.5 MPa 时(虚线最高点)，此时偏度为负值，分子共产生8 个团簇，其中最大团簇包含2973 个CO2分子，分子间空隙减小，表现为类液体特征.

4 结论

本文通过NIST 数据库计算了CO2的相关物性，发现由吉布斯热力学势的二阶导数确定的物性参数，在不同温度下临界行为对应的压力值，同分子动力学模拟中密度时间序列曲线波动幅度相关，提出可以通过时间序列曲线的变异系数来确定S-CO2的Widom 线范围;通过分析偏度并结合聚类分析，提出可通过偏度值对S-CO2类液区和类气区进行界定，得到以下结论.

1) S-CO2在近临界区Widom 线的确定可通过连接时间序列曲线变异系数极大值点来确定，它沿着临界点开始延伸直到350 K 时停止;由变异系数确定的Widom 线可近似替代不同参数在此范围内异常值的连线，但仅通过变异系数无法判别类液区和类气区结构特征.

2) S-CO2类液区和类气区的分子分布结构可以用密度时间序列的偏度来区分.它在类气态时为正，在类液态时为负，在Widom 线上达到最大值.