基于阻尼LSQR-LMBC 的火焰三维温度场重建*

单良 赵腾飞 黄荟云 洪波 孔明

1) (中国计量大学信息工程学院，浙江省电磁波信息技术与计量检测重点实验室，杭州 310018)

2) (中国计量大学计量测试工程学院，杭州 310018)

光场相机可以解决辐射测温多相机系统光路复杂、同步触发难等问题，在辐射成像三维温度重建时有其独特优势.LSQR 是求解基于大型稀疏矩阵最小二乘问题的经典算法，该算法用于重建三维温度场时对温度初值依赖较大，在信噪比较低的情况下重建精度不理想.本文提出阻尼LSQR-LMBC 重建算法，通过在LSQR方法中添加阻尼正则化项，提高火焰三维温度场重建的抗噪性能，并结合LMBC 算法，实现吸收系数和三维温度场同时求解.在数值模拟部分，随着信噪比逐渐降低，阻尼LSQR 的重建效果比LSQR 更加稳定，在信噪比达到13.86 dB 时，重建精度大约提高30%.阻尼LSQR-LMBC 的平均重建误差为6.63%.用丁烷火焰进行了实验，重建的丁烷火焰三维温度场分布符合辐射火焰燃烧的特征，和热电偶的测温数据结果进行对比，相对误差在6.8%左右.

1 引言

温度是火焰燃烧评价的重要参数之一，温度的研究有助于探究燃烧的本质和规律，推进燃烧理论和技术的发展[1].对于三维温度场的测量，接触式测温技术会破坏火焰的原本形状和温度分布，要得到整个燃烧场的温度信息，就必须合理布置测量点，通过估算得到温度场的近似分布，这样会大大增加测量系统的复杂度[2].非接触式测温最显著的特点就是不对流场造成扰动，具有测温范围宽，动态响应灵敏等优点.目前的光电探测元件技术发展相当成熟，CCD 探测器可以非常好地采集火焰辐射强度信息，反演火焰的二维和三维温度场信息，具有非接触、准确度高、实时性好等优点，受到国内外科研人员的青睐.

王式民等[3]结合单CCD 相机与光学分层成像法对火焰的三维温度场进行重建，其通过调整相机采集不同聚焦平面的二维图像进行叠加，最终得到烛光火焰的三维温度场，但是在调焦过程中出现的延时误差无法实现瞬态火焰的温度重建.黄群星等[4]将截断奇异值分解(Truncate singular value decomposition，TSVD)的正则化方法应用于三维火焰温度场重建中，较好地解决了重建问题的不适定性.Gilabert 等[5]提出一种采用多CCD 结合光学层析技术对火焰进行三维温度重建的方法.多相机系统虽然可以获取火焰不同方向的火焰辐射信息，但是相机系统的复杂度会随着CCD 数量的增加而增加，同时也会带来相机的同步问题.Hossain等[6]将传统CCD 相机采用基于投影的CT 层析方法对火焰的三维温度场进行重建，但是层析法实现三维温度场测量时存在需求设备多、光路复杂、耗时长等常见弊端.陆永刚等[7]通过电动机改变传统相机的拍摄位置对火焰进行移焦拍摄，再通过光学分层技术实现了火焰的三维重建，但是火焰的形状是动态变化的，移焦拍摄会出现较大的延时误差，难以采集到同一时刻下的火焰辐射图像序列.

光场相机作为一种新型的图像采集设备，逐渐在三维重建上得到应用和发展[8-14].光场相机是利用微透镜阵列得到图像，可以获得比传统相机更丰富的四维数据信息(光线的强度信息和方向信息)，再结合成像理论和重建算法实现物体的三维重建.Fahringer 等[15]提出了一种基于单个全光相机的三维三分量粒子图像测速技术.Horstmeyer 等[16]利用光场架构，将滤光片与光场相机相结合构建出一种多模式成像方案，可以以数字的方式对特定光谱和偏振光等信息进行重建.Prevedel 等[17]将光场成像技术引入医学神经系统的研究中，并成功获得了被研究者脑中单个神经元活动图像.聂云峰等[18，19]对光场成像技术的进展进行了探索，根据光场成像原理研制了光场成像系统，开展实验对光场相机的数字对焦能力进行验证，并对离焦对象进行了光谱复原.也有一些研究团队将光场成像技术应用于火焰的三维温度场重建.例如，Yuan 等[20，21]对火焰辐射光场的成像过程开展了深入的研究，并分析和评价了火焰图像的成像特征，奠定了火焰光场成像三维温度场重建的理论基础.东南大学的许传龙团队[22-26]将火焰传输模型与光场成像技术相结合，对半透明介质的火焰光场成像特征展开了一系列的研究，并构建了基于光场相机的火焰成像系统，对火焰进行了三维温度场的重建.

本文在光场成像的基础上，将阻尼LSQR(Damped least squares QR decomposition，LSQR)和LMBC (Levenberg-Marquardt with boundary constraint，LMBC)算法相结合，在火焰温度场的反演重建算法上进行了新的探索与尝试.利用双平面参数法对光线进行追迹，通过光场重建策略进行辐射光场的正向模拟实验，使用阻尼LSQRLMBC 的混合算法对模拟光场图像进行反向温度场重建.对丁烷火焰的三维温度场进行重建实验，并使用热电偶对重建结果进行对比分析.

2 原理与方法

2.1 光场成像模型

本文采用的传统一代光场相机，成像示意如图1 所示，其主要由主透镜、微透镜阵列以及CCD图像传感器组成.光源点发射出不同方向的光线，经过主透镜后再穿过微透镜阵列投射到CCD 面成像，同一物点出发的不同方向的光线投射到同一微透镜下的不同像素点，因此光场图像传感器的像素点获取的信息包含方向信息[27].

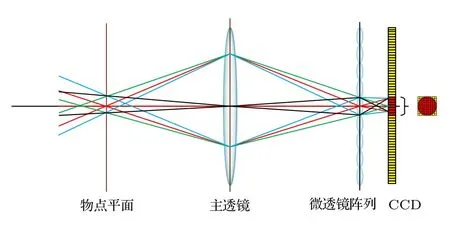
图1 光场相机结构示意图Fig.1.Structure diagram of light field camera.

本文将三维火焰中的某一个体积很小的区域定义为虚拟微元体.在对火焰进行三维温度场重建时，由于虚拟微元体的体积很小，因此可以将其视为点光源，再根据双平面参数法对光线进行追迹定位.根据光场相机的内部光学器件的结构顺序可知，微元体发射出的光线到达光场相机图像传感器面的追迹过程及对应的光线追迹模型如下.

1)从微元体出发的光线经过自由空间到达主透镜平面:

2)光线经过主透镜:

3)透过主透镜的光线经过自由空间到达微透镜平面:

4)光线经过微透镜:

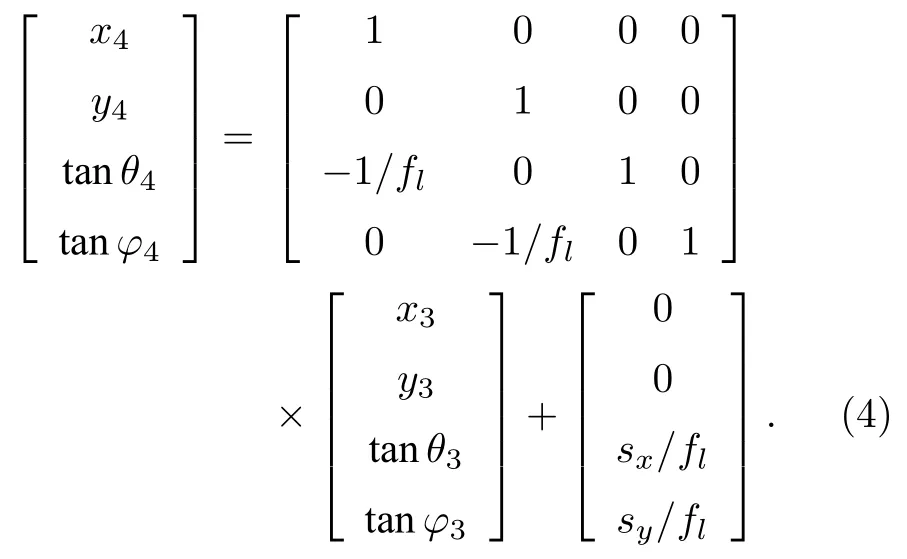
5)透过微透镜的光线经过自由空间，最终投射在图像传感器面:

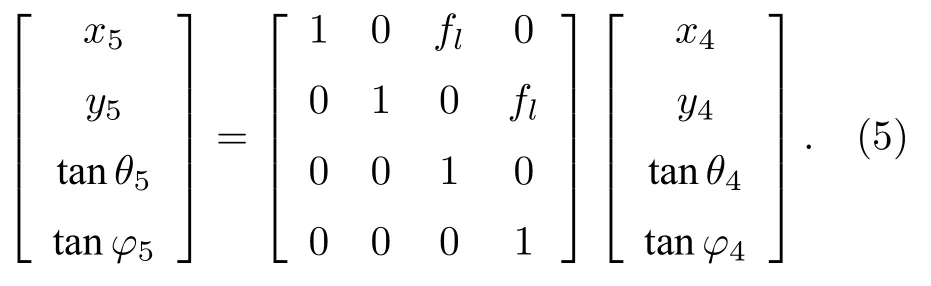
式中，x和y分别表示光线穿过某个平面时对应的光线交点位置坐标，下标对应不同的平面;s0和si分别对应物距和像距;fm和fi分别表示主透镜和微透镜的焦距;sx和sy表示微透镜中心与Z轴的偏移距离.对θ和φ的数值可以利用正余弦定理，通过光场相机内部元器件的参数和器件之间的距离计算得到.

2.2 火焰辐射光场成像模型

火焰的辐射强度值通过图像传感器接收到的光线辐照强度进行分析，采用稳态传输方程进行计算[28].在较短的曝光时间下可以忽略火焰动态变化，直接考虑传输过程中火焰辐射能量对于介质的散射、发射和吸收特性.根据Mie 理论，由于炭黑颗粒的吸收能力远大于散射能力，因此可以忽略火焰的散射特性，仅考虑火焰的吸收特性，火焰的稳态传输方程可以表示为

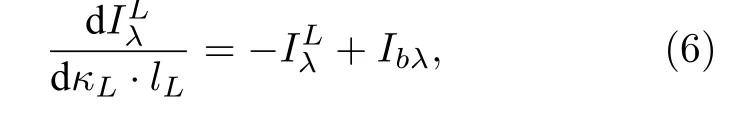
式中，T为微元体的温度，单位为K;c1和c2为辐射常数，分别为3.7418×10—16W·m2和1.4388×10—2m·K;λ为火焰辐射光线的波长.

在进行火焰的三维重建时，需要将被测对象划分为W个微元体，并依次编号为 (1，2，w，···，W)，光场相机的图像探测器一共有M个子像素，依次编号为 (1，2，m，···，M).像素m的火焰辐射光线穿过n个微元体，沿着光线的传输方向依次编号为(w1，w2，wi，wj，···，wn)，将 (6) 式离散化得到 (8)式和(9) 式:

所有辐射光线的光谱辐射强度计算用 (10) 式的矩阵形式表示:

2.3 阻尼LSQR-LMBC 算法

在已知吸收系数的条件下，光场火焰图像的三维温度场重建问题属于线性反问题.然而，在进行实际火焰的测量时，火焰的吸收系数等物性参数是未知的，温度重建为线性问题和非线性问题的混合问题.为对实际火焰进行温度场的计算，很多研究人员将非线性算法与线性算法相结合，如孙俊[29]提出非负最小二乘(Non-negative least squares，NNLS-LMBC)的混合算法，孙俊阳[30]提出Tikhonov-LMBC 的混合算法，这两种算法都可以在火焰三维温度场的重建过程中同时计算温度和吸收系数.本文使用阻尼LSQR-LMBC 混合算法对吸收系数未知的火焰进行三维温度场重建.

阻尼LSQR 是在LSQR 的基础上添加n个阻尼方程[31]，目的是为了解决LSQR 算法对初始值的依赖.(10) 式所示的温度重建线性问题的目标函数如式(11)所示:

其中，m为像素点的个数，n为火焰划分后的微元体的数目，I为单位矩阵，λ表示阻尼因子，是一个实常数.再转换为 (12) 式，结合Lanczos 迭代法利用最小二乘QR 分解算法进行求解[32]，当λ为0，阻尼LSQR 算法为常规标准的LSQR 算法，rIλ(m×n)-A(m×n)Ibλ为残差向量.

阻尼LSQR-LMBC 混合算法的目标函数为

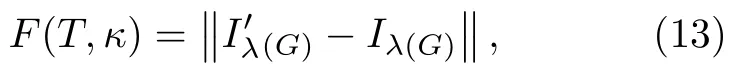
式中，函数均在单色(G)辐射强度的前提下进行计算，Iλ(G)为火焰辐射光线的单色辐射强度观测值，为火焰辐射光线的单色辐射强度估计值.该算法的具体步骤如下:

1)根据目标函数采用的单色辐射强度，选择性地将像素点的光线辐射强度Iλ(R)或者Iλ(G)输入.选取单位向量或者随机向量作为吸收系数的初值，这是因为LM 算法对初值没有依赖性.对中间参数设置迭代次数k0，最大迭代次数为kmax300，v2，η2，吸收系数的向量为κκ0.然后对以下各参数进行计算，参数ω，r，g，Stp，μ分别为对称矩阵、观测值和估计值的差值向量、目标函数的梯度向量，循环终止指数和衰减系数.式中参与计算的参数J和ωii分别表示函数关于变量κ的一阶偏微分雅各比矩阵和矩阵ω对角元素:

2)根据设置的单位向量或者随机向量的吸收系数初值κ对系数矩阵A进行计算.再通过阻尼LSQR 算法对火焰微元体的单色辐射强度Ibλ(G)进行计算:

3)利用已经计算出的火焰温度T和系数矩阵A，再通过 (15) 式对火焰光线的单色辐射强度值进行计算.

4)计算一阶偏微分雅各比矩阵J，根据步骤1)中(14)式对ω、r、g进行计算，通过计算出的参数求解得到优化步长 Δ (κ):

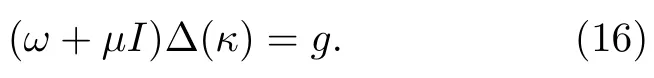
5)判断计算的结果是否满足 (17) 式所示的终止条件，如果满足，则将循环终止指数Stp置为1，同时将运算进程转到步骤8).反之，将 Δ (κ)叠加于κ得到新的吸收系数κnew，再将新的吸收系数投射到吸收系数的约束空间Q:

其中，l([l1，l2，···，lm]) 和u([u1，u2，···，um])分别为约束区间Q的下边界和上边界.

6)对迭代指数ρ进行计算，并判断ρ是否大于零，当大于零时，转入(20)式和步骤8)，反之，继续往下执行:

7)根据 (20) 式对原吸收系数进行更新，再重复对ω，r，g进行计算，对ν 取值2，继续对Stp和μ进行计算:

8)判断终止指数是否满足Stp0，同时判断迭代次数是否满足k＜kmax，如果满足这些判断条件，运算进程转回步骤2)，反之，结束循环，进一步采用阻尼LSQR 算法对火焰的单色辐射强度Ibλ(R)进行计算，最后计算出火焰的温度.

3 火焰温度场重建实验

3.1 数值仿真

根据火焰辐射光场成像模型，利用光线追迹对火焰辐射图像进行成像模拟.本文采用 (21)和(22) 式火焰分布模型，其中，T为火焰温度大小，单位为K，z为火焰的轴向坐标，r为火焰的径向坐标.该模拟火焰符合火焰温度分布特点，火焰底面半径R和高度Z均为40 mm，火焰的温度分布满足旋转对称分布.得到的火焰温度分布如图2 所示，温度最高能达到2100 K.光场相机的参数为:主透镜焦距为50 mm，微透镜焦距为0.6 mm，微透镜阵列大小为60*60，每个微透镜直径上覆盖6 个像素，像素尺寸为8 μm*8 μm，采用光场相机1.0模型，微透镜放置在主透镜一倍焦距处，图像探测器放置在微透镜一倍焦距处.火焰中心与主透镜中心的距离为505 mm.微透镜的数量决定了记录的空间物点数，即空间分辨率，每个微透镜覆盖的像素数决定了记录的光线方向数，即角度分辨率.图像探测器与微透镜的距离决定光场相机获得的有效采样辐射信息，一倍焦距处最低，这个参数主要和本文使用的实验设备的相机模型一致.

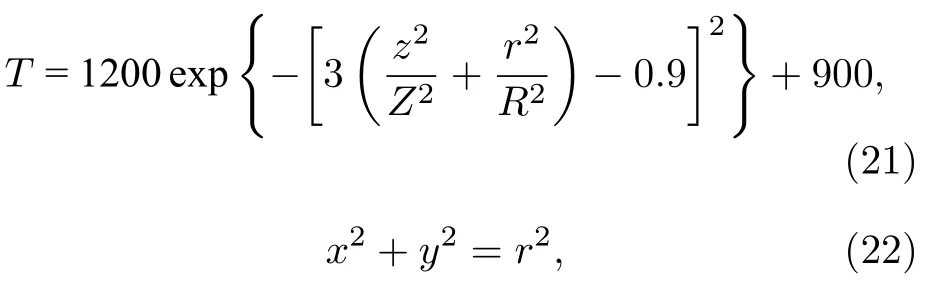
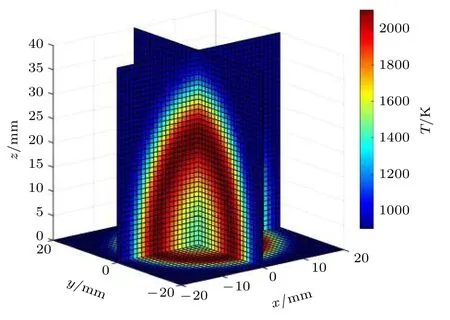
图2 模拟火焰中心切片温度分布Fig.2.Temperature distribution of simulated flame center slice.

以相机主透镜中心O作为原点，Y轴垂直于图像探测器平面，X和Z轴平行于图像探测器平面.沿Y方向对模拟火焰进行切层，每层间隔4 mm.根据光场成像模型，遍历图像探测器上像素的坐标，逆向定位火焰切片上的微元体坐标，将微元体坐标代入 (21) 式得到火焰不同切片的温度值.根据(15) 式计算得到火焰微元体的单色辐射Ibλ，由模拟火焰的光线穿过微元体的数量和设定的吸收系数计算得到 (8) 式中的矩阵A，进而得到图像传感器上的火焰单色辐射强度图，叠加RGB 三个通道的火焰图像即可得到模拟光场火焰图，如图3所示.

图3 模拟火焰光场辐射图像Fig.3.Simulated flame light field radiation image.

分别利用LSQR 算法和阻尼LSQR 算法对火焰温度场进行重建.重建结果如图4 所示，重建时使用原始温度叠加20%的白噪声作为温度初值，一至三行分别为原始火焰分层、使用LSQR 和阻尼LSQR 对火焰光场辐射图像进行温度重建得到的火焰温度分布图.从图4 可以看出，这两种算法均可以完成火焰的三维温度重建.

图4 QR 和阻尼LSQR 算法的火焰温度场重建结果Fig.4.Flame temperature field reconstruction results of LSQR and damped LSQR algorithms.

LSQR 算法是一个对初值有一定依赖的算法[33]，初值的误差对大型稀疏矩阵的求解的影响较为显著，使计算效率变低，甚至无法收敛.为了定量分析LSQR 与阻尼LSQR 的重建精度，在原始温度值上叠加了1%，5%，10%，15%和20%噪声作为初值，从重建结果中提取了120 个采样温度点，将其与相对应的原始温度进行对比分析，如图5 所示.

从图5 可以看出，随着初值叠加噪声的增大，求解值与原始数据之间的差值也逐渐变大.在1%的噪声水平下，LSQR 与阻尼LSQR 的重建误差差距较小，而随着噪声的增大，二者的重建误差差距开始变大，阻尼LSQR 的优点逐渐凸显.当在20%的噪声水平下，LSQR 算法的重建误差在130 K以内，而阻尼LSQR 算法的重建误差在90 K 以内.

图5 不同噪声水平下，LSQR 与阻尼LSQR 算法重建误差对比 (a)初值叠加1%噪声;(b) 初值叠加5%噪声;(c) 初值叠加10%噪声;(d) 初值叠加15%噪声;(e) 初值叠加20%噪声Fig.5.Comparison of reconstruction errors between LSQR and Damped LSQR algorithm under different noise levels:(a) Initial value superimposed 1% noise;(b) initial value superimposed 5% noise;(c) initial value superimposed 10% noise;(d) initial value superimposed 15% noise;(e) initial value superimposed 20% noise.

为进一步从整体上进行算法优劣的对比，将得到的所有重建结果通过 (23) 式进行了相对误差计算:

式中，T为使用重建算法重建出的微元体的温度，Tset为使用 (21) 式设置的火焰的微元体的温度，Δ T为相对误差.得到的误差对比结果如表1 所示.

表1 LSQR 与阻尼LSQR 温度重建结果相对误差对比表Table 1.Comparison of relative errors of temperature reconstruction results of LSQR and Damped LSQR.

通过重建结果可以看出，当初值叠加的噪声较小时，阻尼LSQR 的略优于LSQR.随着叠加的噪声逐渐增大，阻尼LSQR 比LSQR 算法更加稳定，而LSQR 受初值的影响更大，因此阻尼LSQR 更适合大型稀疏矩阵的求解.孙俊[29]采取的NNLS算法和孙俊阳[30]采取的Tikhonov 算法均与LSQR算法进行了对比，虽然与本文的光场相机模型不同，其相对的性能提升仍具有参考价值.对于NNLS算法，随着噪声水平的提高，LSQR 求解结果中的负值越来越多，但NNLS 未出现负值，两种算法重建结果的相对误差十分接近，信噪比为20 dB 时，相对误差在5%左右;信噪比为10 dB 时，相对误差在20%左右，信噪比为5 dB 时，相对误差在40%左右.NNLS 相对LSQR 提升在5%以内，但NNLS的计算时长比LSQR 高了两个数量级.对于Tikhonov算法，噪声较小时，Tikhonov 正则化算法与LSQR算法重建结果的最大相对误差基本一致.当信噪比达到10 dB 时，LSQR 算法重建结果的相对误差在1.8%以内，Tikhonov 正则化算法重建结果的相对误差在1.2%以内，相对提升了约50%.对于本文的阻尼LSQR 算法，当信噪比为13.86 dB 时，LSQR重建结果的相对误差为14.58%，阻尼LSQR重建结果的相对误差为10.99%，相对提升了32.7%.从计算时间上看，本文方法和LSQR 处于同一量级，计算的实时性对火焰来说也是一个比较重要的因素.

对于实际的火焰温度测量，火焰的吸收系数等物性参数是未知的，因此利用阻尼LSQR-LMBC混合算法对模拟火焰辐射光场图像的吸收系数和温度同时重建.火焰以4 mm 的间隔对火焰进行分层，重建温度分布如图6 所示.图中的火焰温度分布图可以正确的反映火焰的温度趋势特征，但是重建温度的精度有待提高.

图6 阻尼LSQR-LMBC 算法下重建的火焰温度分布图Fig.6.Flame temperature distribution reconstructed by Damped LSQR-LMBC algorithm.

为了进一步对重建结果进行分析，本文对重建后的前五层温度进行误差分析，将计算出的每一个微元体的温度与相对应的原始温度进行相对误差的计算，其结果如图7 所示.

从图7 可以看出，该算法的总体重建误差在1.92%—17.2%之间.所有微元体的平均误差为6.63%，因此该重建算法可以满足高达2100 K 的火焰温度重建.

图7 阻尼LSQR-LMBC 算法重建的火焰温度的相对误差 (a) —16 mm 位置;(b) 火焰—12 mm 位置;(c) —8 mm 位置;(d) —4 mm位置;(e) 0 mm 位置Fig.7.Relative errors of flame temperature reconstructed by Damped LSQR－LMBC algorithm:(a) —16 mm position;(b) —12 mm position;(c) —8 mm position;(d) —4 mm position;(e) 0 mm position.

3.2 辐射强度标定

光场相机图像传感器在对火焰进行辐射信息采集时，辐射光线会先经过光电转换、模数转换等过程再以灰度值的形式展示.因此，需要对光场相机的图像传感器进行辐射强度标定，建立灰度值与光线辐射强度之间的关系，进而保证重建温度的准确度.实验装置如图8 所示.使用的黑体炉是由英国爱松特公司生产的，型号为ISOTECH Cyclops Model 878，温度最高可以达到1573.15 K，精度为0.1 K，辐射率为0.999.相机为一代传统光场相机，型号为Lytro-Illum[34，35]，主透镜焦距为40.11 mm，微透镜焦距为48.38 μm，角度分辨率为15×15，空间分辨率为434×625.通过Lytro-Illum 光场相机拍摄得到的光场图像为LFR 格式，其中包含了原始光场图像和拍摄时的参数信息.解码时首先根据相机自带的白图像标定微透镜阵列的位置坐标，微透镜下覆盖的像素记录了来自同一物点不同方向的光线，这些像素集合又被称为宏像素.每个宏像素中相同坐标的像素点记录相同方向的光线，提取记录相同方向光线的像素，按照宏像素位置排列即可得到2D 单视角图像.依次提取不同方向的单视角图像，按照记录的方向排列即可得到多视角图像.

图8 光场相机辐射强度标定实验装置图Fig.8.Experimental deviceofradiation intensity calibration of light field camera.

为避免其他杂光对标定实验产生影响，在黑暗条件下，通过黑体炉温度从1098.15 K 开始，以25 K 的温度间隔采集了8 组黑体辐射光场图像，如图9 所示.

普朗克定律指出，在黑体的条件下，在指定温度下的辐射强度值可以通过 (24) 式计算:

式中，E(λ，T) 为波长λ处的光谱辐射强度值，ε(λ)为波长λ处的黑体发射率，取值为1，T为黑体的温度值，c1，c2分别为第一辐射常数和第二辐射常数，其值大小分别为 3.74177×10-16W·m2和1.4387752×10-2m·K.

对光场图像标定区域的灰度值进行提取，再分别将R，G，B通道的灰度值与辐射强度值进行曲线拟合，得到的拟合结果如 (25) 式—(27)式所示:

式中，IR，IG，IB分别为光场图像的R，G，B通道下像素对应的光谱辐射强度值，R，G，B分别为光场图像的R，G，B通道下像素对应的灰度值.光场辐射强度标定结果对应的拟合曲线图如图10 所示.

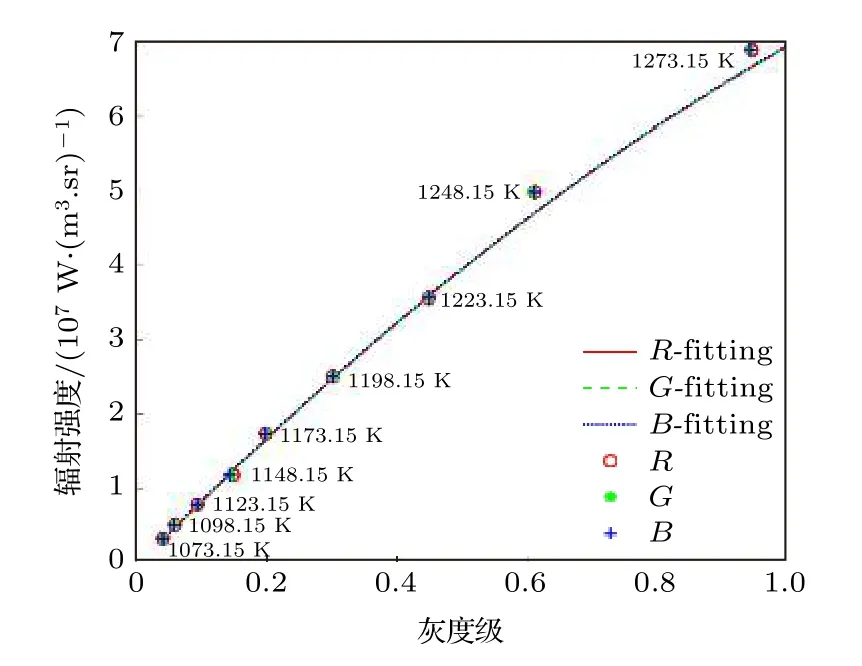
图10 光场图像灰度值与辐射强度的标定拟合曲线图Fig.10.Calibration fitting curve of gray value and radiation intensity of light field image.

3.3 实际火焰温度重建

实际火焰的三维测温装置主要有光学平台、光场相机以及火焰发生装置等.将实验器材固定在光学平台上，通过光场相机对火焰进行图像的采集.实验装置图如图11(a)所示，图中的丁烷气罐的燃烧火焰，火焰发生器的喷嘴直径为20 mm.

在对火焰进行图像采集时，要记录火焰与相机之间的距离，并且保证火焰处于空气流动很微弱的暗室实验环境中.同时，需要合理控制相机的曝光时间，确保采集到的火焰图像像素灰度值不会出现曝光过度，降低曝光不足带来的影响.通过光场相机采集的丁烷火焰辐射光场图像如图11(b)所示，火焰与光场相机之间的距离为15 cm.

图11 燃烧火焰实验图 (a) 实验装置;(b) 丁烷火焰辐射光场Fig.11.Experimental diagram of combustion flame:(a) Experimental device;(b) light field of butane flame radiation.

根据相机与火焰之间的距离以及相机内部的参数等已知数据，利用 (1) 式— (5) 式所示的双平面参数法将光场辐射图像的方向信息转换为三维空间的火焰位置信息.得到火焰的三维位置信息后使用微元体分割方法对火焰进行网格划分.通过辐射标定结果将图像灰度值幻化为辐射强度值，再利用阻尼LSQR-LMBC 混合算法对火焰的吸收系数和温度同时重建，结果如图12 所示.

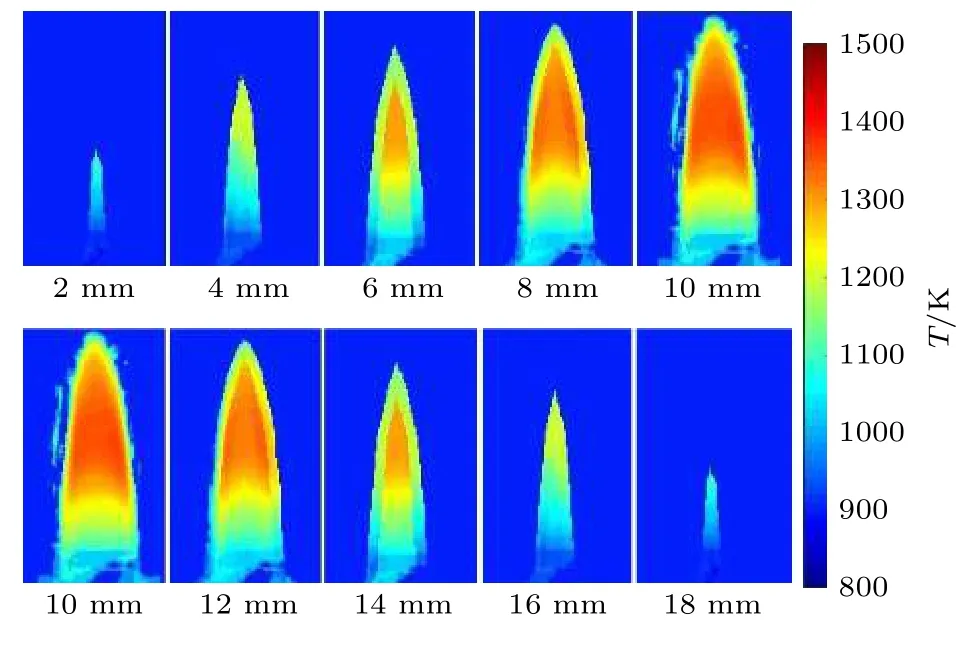
图12 丁烷火焰三维温度重建后的不同层温度分布图Fig.12.Temperature distributions of different layers after three-dimensional temperature reconstruction of butane flame.

由丁烷发生器的喷嘴大小可知火焰的最大直径为20 mm，图中将火焰在2 mm，4 mm，6 mm，8 mm，10 mm，12 mm，14 mm，16 mm，18 mm处进行竖直切片得到的各层温度，其中10 mm 处的温度分布图为火焰的中心层.由于该火焰近乎旋转对称，因此火焰在12 mm，14 mm，16 mm，18 mm处的温度分布图分别与8 mm，6 mm，4 mm，2 mm处的温度分布图近乎一致.图中重建火焰的最高温度在1400 K 左右，不超过1500 K.从10 mm 层的温度分布图中可以看出，火焰满足焰心、內焰和外焰的温度分布趋势.外围的温度会出现低温度区域的原因是由于火焰的温度出现流失，扩散到了低温的空气中，这也是2 mm 和18 mm 处的温度较低的原因.而8 mm 与12 mm 处的火焰切片的较大区域为內焰和外焰，火焰较为明亮，温度也较高.6 mm 与14 mm 处的火焰温度切片的面积已经明显变小，外焰和內焰的混合使得火焰的温度较高.4 mm 和16 mm 处的火焰温度已经逐步扩散到空气中，温度也有所降低.综上，重建的丁烷火焰的三维温度场分布符合基本辐射火焰燃烧的特征.

为进一步对重建结果进行准确度验证，使用热电偶对火焰进行定点测温，装置如图13(a)所示.选取不同位置的特征点进行测温，测温点的选取如图13(b)所示.热电偶在测量时，其测量点和周围环境之间存在辐射换热和对流换热，从而导致产生热损失，为了减小引起的测量误差，需要使用 (28)式对测量结果进行修正[36]:

图13 使用热电偶测量丁烷火焰温度 (a) 热电偶测温实验图;(b) 热电偶定点测温位置图Fig.13.Measurement of butane flame temperature using thermocouples:(a) Thermocouple temperature measurement experiment diagram;(b) location diagram of thermocouple fixed-point temperature measurement.

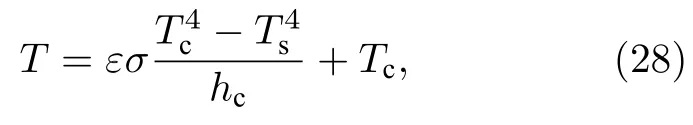
式中，T表示修正后的温度值;Tc和Ts分别为测量的原始温度和实验环境温度，实验时室温控制在293.15 K 左右;ε表示热电偶探头发射率，实验中使用的是K 型热电偶，数值为0.89;σ表示斯蒂芬-玻尔兹曼常数，数值为5.67×10—8W/(m2·K4);hc表示对流换热系数[29].

将重建温度和热电偶修正温度进行比对，如表2 所示.

从表2 可以看出，重建温度与热电偶的测温数据基本一致.其中测量偏差的平均值为76 K 左右，最大偏差约为89 K.测温误差控制在6.8%左右，因此本研究的重建方案的测温精度满足火焰的测温标准.

表2 阻尼LSQR-LMBC 重建温度与热电偶修正温度对比表Table 2.Comparison of DampedLSQR-LMBC reconstruction temperature and thermocouple correction temperature.

4 结论

1) 本文针对经典算法LSQR 在求解火焰三维温度场时对初值依赖大的问题，通过添加阻尼正则化项，提高了火焰三维温度场的抗噪性能，仿真结果表明:在较低的噪声水平下，这两种算法的重建误差基本一致，当噪声较大时，阻尼LSQR 算法的重建精度比LSQR 算法高30%左右.鉴于实际火焰的吸收系数未知，使用阻尼LSQR-LMBC 算法对吸收系数该火焰进行数值计算，实验结果表明:火焰重建的相对误差在1.92%—17.2%之间，平均误差低于7%.证明了阻尼LSQR-LMBC 算法可以同时重建火焰的吸收系数和温度.

2) 开展了实际火焰温度重建实验研究.搭建了光场成像的火焰三维温度场重建的实验平台，标定了光场相机图像传感器的辐射强度，对丁烷火焰的三维温度进行重建，并将热电偶的测量结果作为参考火焰温度，将其与重建后的结果进行对比分析和精度评价.结果表明:火焰重建的温度与热电偶测量的温度基本一致，平均偏差均低于100 K，重建误差在6.8%左右，