辐照损伤对钨晶格热导率影响的分子动力学研究

冉玉柱， 康 瑶， 王旭东， 姚 曼

(大连理工大学 材料科学与工程学院， 大连 116024)

1 引 言

钨(W)在室温下的热导率高达174 W/(m·K)，且具有高熔点(3410℃)、低溅射、不形成氢化物等优点，因此W被认为是最有前景的面向等离子体材料(PFM)[1, 2]. 在核聚变装置中，PFM直接暴露于高能中子和高通量的氢/氦等离子体热流中，这使得材料的导热性能尤为关键. 然而，在强烈的辐照环境下材料近表面的微观结构会发生显著变化，如高能中子可穿过钨表面并与内部原子发生碰撞[3]，被撞击的点阵原子称为初级碰撞原子(PKA)，进一步产生级联碰撞并最终在材料内部形成Frenkel缺陷[4]，此外，高通量的H/He等离子辐照会在钨中的晶界和空位等缺陷处聚集形成H或He泡. 这些由辐照产生的结构缺陷会对钨的近表面区域的导热性能产生显著影响[5-9]，Tokunaga等人通过对金属钨进行氦粒子束的高热负荷实验，发现辐照损伤深度达到150 nm且在钨表面区域形成气泡，造成局域热负荷致使表面区域熔化[10]. 在实际核聚变反应堆中，H+、He+和中子等辐照同时存在并产生协同作用，对材料造成更加严重的损伤. 这些缺陷引起的局域的瞬态热负荷将严重侵蚀反应堆结构材料，因此，研究辐照作用下钨的导热性能具有重要的意义.

材料的热导率主要由电子和声子导热贡献，已有相关研究表明室温下钨的晶格热导率约为其总热导率的10%[11-13]. 然而钨的辐照损伤主要是由原子位移引起的，与晶格动力学直接相关，因此系统地研究各类辐照作用造成的结构缺陷对声子热导率的影响有助于我们理解钨的辐照损伤机理. Hu等人采用分子动力学方法研究发现纳米级氦气泡使单晶钨的晶格热导率降低了80%[11]. Fu等人采用分子动力学方法分别探究了温度、晶向和晶界对钨导热性能的影响，结果表明钨的晶格热导率具有一定各向异性，且随温度升高而降低，晶界区域晶格热导率约为单晶钨的10%[12]. 实际辐照环境下，钨的近表面区域会产生各种辐照损伤相关的缺陷，但这些结构缺陷对钨导热性能的影响和相关机理尚不清晰.

本文模拟了辐照诱发的点缺陷随时间的演化过程，并分别构建了包含Frenkel缺陷对、空位、间隙原子、氦气泡和晶界等缺陷的晶体钨结构模型，通过非平衡分子动力学(NEMD)方法系统地分析对比了不同缺陷对钨晶格热导率的影响.

2 研究方法

本文采用Müller-Plathe NEMD方法[14]模拟计算钨的晶格热导率，所有NEMD模拟均在Lammps软件[15]下进行. 首先构建20 × 20 × 60个单胞组成的三维单晶钨的结构模型(包含48000个原子)，晶格常数取3.162 Å. 如图1所示，模型结构两端分别固定4层钨原子，以防止原子逸出丢失，并在模型两端分别设置4个晶格长度的热区和冷区，在z轴方向应用非周期性边界条件，在x和y两个方向上应用周期性边界条件，采用Finnis和Sinclair[16]开发的嵌入原子势(EAM)描述钨原子之间相互作用，时间步长为1 fs. 首先，采用berendsen恒温器将模拟体系以恒定的体积和300 K温度弛豫了400 ps，充分弛豫并达到稳定状态，然后关闭恒温器，并用速度重新标度(velocity rescaling)方法在体系一侧的热区以恒定速率注入能量产生热源，并在另一端用相同的速率移除热量，可在模型的z轴方向上产生热流，等体系达到稳定状态后，取4～7 ns内的平均温度得到模型沿z轴方向上的温度分布曲线，进而利用傅里叶定律[17]可计算得到晶格热导率k：

(1)

式(1)中，J为沿z方向施加的热流，dT/dz为z方向的温度梯度.

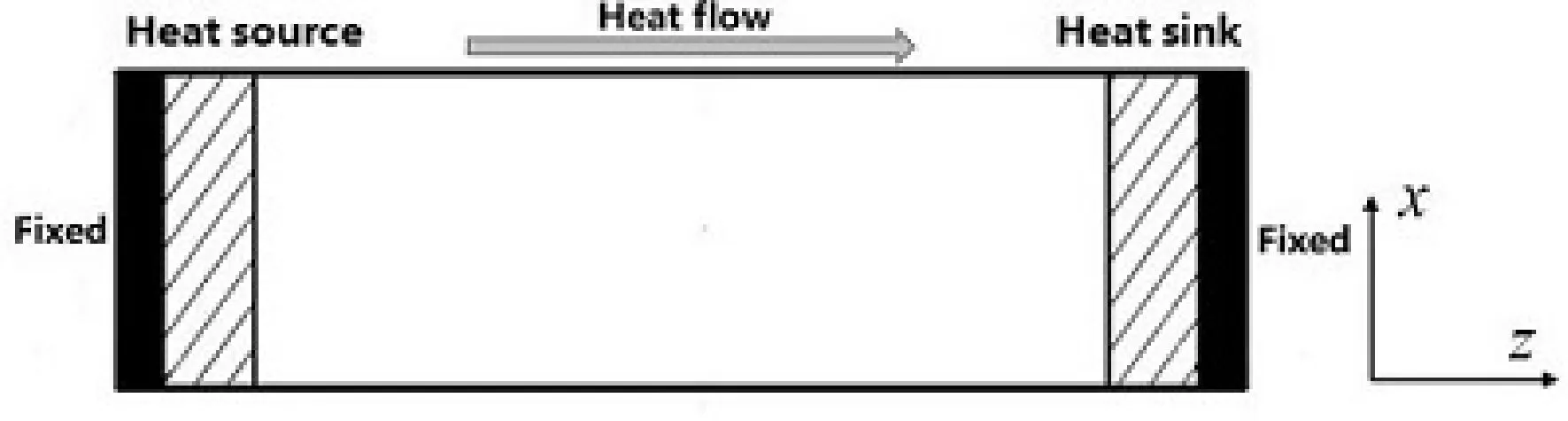
图1 用于计算钨热导率的NEMD模型示意图Fig.1 Schematic of NEMD simulation model for computing the lattice thermal conductivity of tungsten

3 结果与讨论

3.1 不含缺陷晶体钨的晶格热导率

图2所示为300 K下模拟得到的单晶钨的温度曲线，其中线性区域选择为40～145 Å以避免模型冷热区边界附近的非线性区域. 根据得到的温度梯度，代入公式(1)可以得到完美晶体钨的晶格热导率为14.5 W/(m·K)，与已有的相关计算结果(13～15.6 W/(m·K))基本一致[11, 12]，证明模拟结果的有效性.

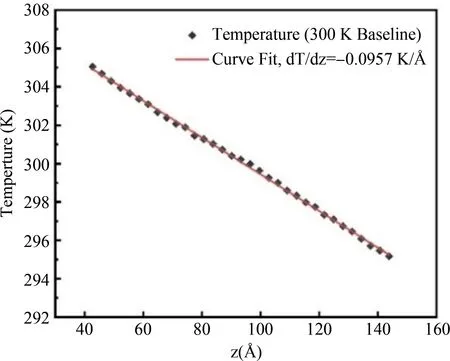
图2 300 K下单晶钨线性区域的温度分布曲线Fig.2 Temperature profile for single crystal tungsten at 300 K

3.2 中子辐照诱发的Frenkel缺陷对钨晶格热导率的影响

为了探究高能中子对钨晶格热导率的影响，模拟了PKA在材料内部的级联碰撞过程，如图3(a)上方的模型图所示，在模型靠近中间位置随机选取一个原子作为PKA，能量设为1.5和3.0 keV，速度方向沿z轴方向. 图3(a)下半部分显示为级联碰撞过程中材料内Frenkel缺陷对的数目随时间的演化曲线. 可以看出在不同PKA能量下，点缺陷数都随时间先增加后减少，最终会在材料内部留下空位和间隙原子成对存在的Frenkel缺陷对，这与预期的级联碰撞过程结果一致[18]. 辐射中子的能量越大，产生的PKA的能量也越大，最终在模型中留下的缺陷数目也越多，取三次模拟的平均值得到能量分别为1.5和3.0 keV的PKA在钨内部产生的Frenkel缺陷数目分别为～6.3和～13.7个. 然后，如图3(b)和(c)所示，计算了包含这些点缺陷的单晶钨的晶格热导率，可以看到模型中间缺陷位置处的温度梯度明显大于其它不含缺陷的部位，且与图2不含缺陷的单晶钨相比，模型两端温差增大，表明含缺陷单晶钨的导热性能降低.

图3 (a)不同PKA能量对应的钨内缺陷数随时间的演化，PKA能量分别为1.5 keV (b)和3.0 keV (c)时稳定阶段Frenkel缺陷(红球代表间隙原子；篮球代表空位)的分布及体系的温度分布曲线Fig. 3 (a) Number of defects in tungsten as a function of time under different PKA energies, and the Frenkel defects distribution (the red balls denote interstitial and the blue balls denote vacancy) and temperature profile for the structure model with PKA energies is 1.5 keV (b) and 3.0 keV (c)

与图2不同，从图3(b)和(c)可以看到，温度曲线因点缺陷的引入被分为三段，缺陷区域的晶格热导率明显下降，其中能量为3 keV的PKA产生的缺陷区域(图3(c)的S2)的晶格热导率为6.7 W/(m·K)，远低于完美晶体钨. 为了确定含缺陷模型的有效晶格热导率(keff)，需要得到每个区域的热阻，当热量在物体内部以热传导方式传递时，热阻R可表示为：

R=L/kA

(2)

式(2)中，L代表长度，k为热导率，A为垂直热流方向的截面积. 将模型每段的温度梯度代入式(1)可得到对应的晶格热导率，并由式(2)计算得到每段的热阻，然后将求和得到的整段模型的总热阻R、长度L和截面积A代入式(2)即可求得含Frenkel缺陷的单晶钨模型的有效晶格热导率[19, 20]. 计算结果列于表1，可以看到Frenkel缺陷使得体系的有效热导率降低，PKA能量为1.5和3.0 keV时，对应的晶格热导率分别下降了10.3 %和18.6 %.

表1 不同PKA能量(EPKA)对应的体系内缺陷数量(N)、有效晶格热导率(keff)及热导率下降的百分比

3.3 中子辐照对多晶钨晶格热导率的影响

为了探究中子辐照诱发的点缺陷与晶界(GB)的相互作用及对多晶钨的晶格热导率的影响，构建了如图4(a)左侧图所示的Σ13[001](150)对称倾斜晶界模型，其中是重合位置点阵参数，代表重合位置密度的倒数，[001]为旋转轴，(150)为对称面. 在距晶界中心1.5 nm处选择一个原子作为PKA，设置其能量为3 keV，速度方向垂直于晶界. 图4(a)右侧图分别显示了级联碰撞产生的点缺陷峰值区和稳定阶段的分布，其中蓝球和红球分别代表晶粒内部的空位和间隙原子，由于晶界内没有点缺陷的概念，绿球和黄球代表晶界内受级联碰撞影响发生明显位移的原子. 稳定阶段晶粒内部存留的空位和间隙原子数目分别为～8.5和～4.3个，而中子辐照产生的Frenkel缺陷对，间隙原子和空位总是成对出现. 这是由于在钨中，空位的迁移能垒(1.8 eV)远大于间隙原子迁移能垒(0.002 eV)，与空位相比，间隙原子更易于扩散并在晶界区域偏聚，进而对晶界结构造成影响.

如图4(b)所示，分别计算了辐照前后晶界体系的晶格热导率，晶界区域晶格热导率为1.1 W/(m·K)，远远小于晶粒内部，这是由晶界不规则的原子排布且晶界两侧晶粒取向的不同导致的. 且辐照前后晶界区域晶格热导率基本相等，说明3 keV能量的PKA对晶界区域晶格热导率影响较小. 辐照前后晶界体系的有效晶格热导率分别为4.4和4.0 W/(m·K)，辐照后的晶格热导率下降了约9%.

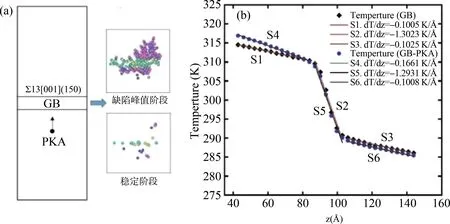
图4 (a) 晶界模型示意图及3.0 keV能量的PKA产生的点缺陷峰值时刻和稳定阶段的分布(蓝球和红球分别代表晶粒内部的空位和间隙原子，绿球和黄球代表晶界内发生明显位移的原子)，(b) 辐照前的晶界体系(GB)和辐照后稳定阶段的晶界体系(GB-PKA)的温度分布曲线Fig.4 (a) Schematic diagram of GB and the defects distribution at peak moment and stable moment with EPKA=3 keV, (b) the temperature profiles of undamaged and damaged GB models

3.4 氦气泡对钨晶格热导率的影响

在高通量氦等离子体的辐照作用下，He易于在材料内部的晶界和空位处聚集形成He气泡，显著影响钨的微观结构. 为了研究He气泡对钨晶格热导率的影响，建立了如图5上半部分所示的含He气泡的单晶钨模型，在模型中间部位构建半径为4个晶格长度的球形空洞，并随机放入He原子，密度为0.4 × 1028atoms/m3，在300 K下弛豫至稳定状态，然后施加热流计算模型的晶格热导率，温度分布如图5所示. He气泡区域的晶格热导率明显低于不含He气泡的区域，模型整体的有效热导率为3.6 W/(m·K)，即气孔率(He气泡体积与总体积的比值)为2.1%时，晶格热导率降至完美单晶的～25%. 热导率的下降主要是因He纳米气泡边界处不均匀的晶格扭曲导致了声子的散射.

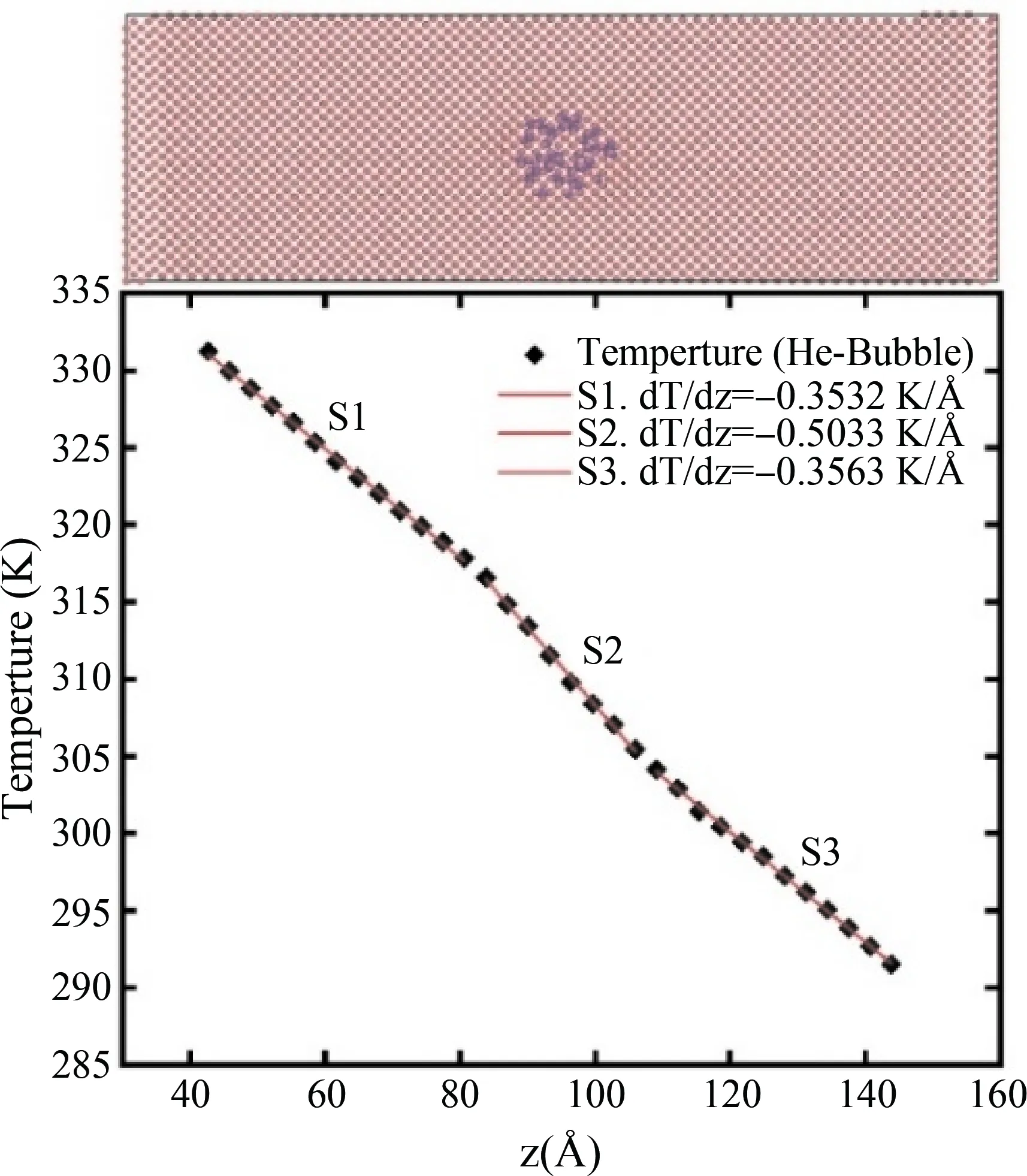
图5 含氦气泡的单晶钨模型(粉色和蓝色球分别代表W和He原子)及温度分布曲线Fig. 5 The temperature profile in tungsten with helium bubble (the red balls denote tungsten and the blue balls denote helium)

3.5 不同浓度的点缺陷对钨晶格热导率的影响

为了探究不同浓度的点缺陷(空位/间隙原子)对钨晶格热导率的影响，在模型中分别随机删除/添加一定原子比例的钨原子，分别构建了含0.3%和0.6%空位(间隙原子)的单晶钨模型，并进一步计算其在300 K下的晶格热导率，计算结果列于表2，可以看到缺陷浓度越高，晶格热导率下降程度越大，0.6%空位和间隙原子分别使晶格热导率下降了约52%和78%. 且相同浓度的间隙原子比空位造成的热导率下降程度更大，这可能是间隙钨原子比空位引起的晶格畸变程度更大而造成了更强的声子散射导致的.

表2 含不同浓度的空位(kv)和间隙钨原子(ki)单晶钨的晶格热导率

4 结 论

本文构建了包含Frenkel缺陷和氦气泡等辐照损伤相关缺陷的晶体钨的结构模型，采用了非平衡分子动力学的方法定量研究了这些缺陷对钨导热性能的影响. 随PKA能量的增加，晶体内部留下的Frenkel缺陷对的数目增多，3 keV能量的初级碰撞原子(PKA)使晶格热导率下降至完美晶体的～81%. 间隙原子更易于向晶界迁移偏聚，造成晶粒内部空位多于间隙原子. 晶体中的纳米级He气泡导致晶格热导率的显著降低，气孔率为2.1%时晶格热导率降至完美晶体的～25%. 与空位相比，钨中的间隙钨原子造成晶格热导率下降程度更大. 这些不同的微观结构缺陷造成钨晶格热导率不同程度的降低，这是由缺陷周围的晶格扭曲增大了声子散射几率导致的.