针对卷积神经网络流量分类器的 对抗样本攻击防御

王 滨, 郭艳凯, 钱亚冠, 王佳敏, 王 星, 顾钊铨

1浙江科技学院大数据学院 杭州 中国 310023

2杭州海康威视网络与信息安全实验室 杭州 中国 310052

3广州大学网络空间先进技术研究院 广州 中国 510006

1 引言

随着互联网的快速发展, 网络流量不断增长并呈现多样化的趋势, 这给互联网运营和管理带来巨大的压力和挑战。网络流量分类作为网络管理与网络安全的一项关键技术, 不但能够优化网络配置, 降低网络安全隐患, 还能根据用户的行为分析提供更好的服务质量, 对于网络管理中心了解网络运行状态、优化网络运营和管理具有重要意义。

传统的流量分类方法主要是基于端口和深度包检测[1-2]。但随着负载加密和新型应用的不断涌现, 导致上述方法的有效性下降。近年来, 研究人员采用机器学习的方法解决网络流量分类问题。机器学习方法利用“网络流”(flow)的统计特征(如网络流的时间长度、数据包的数量等)建立分类模型, 不受动态端口、负载加密甚至网络地址转换的影响。随着深度学习在计算机视觉[3]、语音识别[4]、自然语言处理[5]等多个领域取得的成功应用, 也为流量分类提供了新的技术契机。白雪等人[6]针对P2P流量分类准确率较低的问题, 提出一种基于深度学习结构、半监督的深度置信网络流量分类方法, 实验证明具有良好的效果。Ertam等人[7]通过使用 WK-ELM 算法中的 GA 技术训练神经网络, 针对Moore数据集进行流量分类达到96.57%的准确率。王勇等人[8]提出一种基于卷积神经网络(CNN)的流量分类算法, 构造能够实现流量自主特征学习的分类模型。Wang等人[9]利用CNN方法对恶意流量进行分类识别, 在实际的流量数据集USTC-TF2016上进行了实验, 获得了很高的准确率。由于CNN具有自动提取特征的能力, 通过多个卷积层的深层网络结构, 自主发现学习数据的特征表示[10], 应用于网络流量分类时具有明显的优势。但是, 新的研究又表明CNN容易受到对抗样本的攻击, 即在原始数据上增加一些微小的扰动, 就能导致CNN错误分类[11]。

基于CNN的流量分类器首先把流量数据转换为灰度图像, 因此可以通过图像对抗样本对流量分类器实施攻击, 通过在图像上添加微小噪声, 使CNN发生错误预测。目前典型的对抗样本生成方法有FGSM[12]、DeepFool[13]、JSMA[14]和C&W[15]等。为了能实现对真实场景的流量分类器实施攻击, 我们将表示流量的图像对抗样本再逆变换成攻击数据包流, 向目标CNN重放, 达到攻击目的。实验表明, 本文提出的攻击方法可以成功的攻击CNN流量分类器。

针对对抗样本的攻击, 目前提出了很多防御方法, 例如对抗训练[16-18]、梯度掩蔽[19]、检测防御[20]等, 对抗训练是目前被证实最为有效的防御方法[21]。但目前的对抗训练需要生成大量对抗样本, 大大增加了训练时间, 本文针对网络流量数据量巨大的特点, 提出了批次对抗训练, 利用反向传播误差的过程, 同时完成样本梯度和模型梯度的计算, 加快了训练速度。由于批次对抗训练是已知目标模型的结构、参数, 因此可以很好地防御白盒攻击, 但在防御其它CNN的黑盒攻击方面有不足。我们进一步提出增强对抗训练, 利用样本梯度的余弦相似性, 筛选出不同扰动方向的对抗样本加入到对抗训练, 在保证原分类准确性不受影响的前提下, 增强对跨模型黑盒攻击的防御能力。实验结果表明, 增强对抗训练比批次对抗训练能更好的防御这类黑盒攻击。

2 预备知识

2.1 卷积神经网络

定义1 卷积神经网络(CNN):CNN一般可以表示为映射函数 : ↦F X Y,X∈X是d维输入变量,Y∈Y是一个m维概率向量, 表示m个类的置信度。一个N层CNN输入X后产生的输出:

F(i)代表CNN的第i层的计算输出。这些层可以是卷积、池化或者其他任何形式的神经网络层。CNN的最后一层采用Softmax层, 定义为:

其中,Z= F(N-1)(·)是前一层(又称最后一个隐藏层)的输出向量。最后预测的标签由y= argmaxi=1…mF (X)i得到, 其中 F(X) =Softmax(Z)。

2.2 网络流量分类

本文的CNN流量分类器是针对网络流构建, 即输入X为网络流。原始的网络流量(raw traffic)是由数据包序列组成:P= {p1,…,pN}, 数据包pi= (xi,bi,ti),i= 1,2,… ,N,xi为5元组(源IP地址、源端口、目标IP、目标端口和传输层协议),bi∈ [0, +∞]表示数据包的大小(字节为单位),ti表示数据包传输的起始时间。

定义 2 网络流:一个网络流表示为f= (x,b,dtt), 它是原始网络流量P的子集。这个子集中的所有数据包按时间次序排列: {p1=(x1,b1,t1),… ,pn=(xn,bn,tn)},t1＜ … ＜tn, 且所有五元组相同, 即x=x1= ... =xn。b表示网络流中所有数据包的大小之和,dt=tn-t1表示网络流的持续时间,t表示网络流的起始时间。

基于CNN的流量分类就是找到网络流集合F= {f1,f2,… ,fN} 到 流 量 应 用 类 型 集 合Y= {y1,y2,… ,yk}的映射。由于CNN的输入是二维图像数据, 因此先把原始的流量数据转化为网络流, 再转化为二维矩阵。上述预处理过程如图1所示, 首先将原始网络流量P分割成多个离散的网络流f1,f2,… ,fN; 然后匿名化网络流中的IP地址和MAC地址[22]; 进行数据清洗, 去除重复网络流; 将所有的网络流数据通过填0的方式补齐到相同长度。

图1 网络流量预处理 Figure 1 Network traffic preprocessing

由于网络流的靠前部分通常是连接信息和一些内容数据, 根据经验前784个字节已经可以很好的反映网络流的内在特征[9]。因此本文采用28×28输入的CNN, 所有的网络流截取到784个字节。最后, 将每个数据流转化为28×28大小的灰度图像, 每个像素表示数据流中的一个字节。把这些灰度图像输入到CNN, 训练模型, 获得CNN流量分类器[8]。

3 网络流对抗样本攻击

尽管现有的研究表明, CNN用于网络流量分类具有良好的性能[8], 但正是它具有自动提取特征的特点, 反而成为对抗样本攻击的弱点[11]。我们提出网络流的对抗样本, 即在原始的数据包中加入少量扰动信息, 再重放到网络上。CNN流量分类器采集到这些数据包后, 会转化为灰度图像。由于原始数据中加入了扰动, 会使得CNN产生大量的错误分类, 从而实现攻击目的。

3.1 威胁模型

对抗样本攻击的威胁模型是攻击者根据不同的应用场景、假设和攻击程度要求, 改变攻击方法需要的属性, 部署特定的攻击, 主要包括攻击目标和攻击能力[23]。由于流量分类器通常部署在路由器等设备中, 攻击者无法直接获得CNN的结构和参数。本文假设攻击者仅知道目标模型为CNN, 采取近似于黑盒攻击的策略, 即在本地训练一个代理CNN。利用对抗样本的可转移性, 在代理模型上生成对抗样本, 然后构建伪造数据包, 重放给远程目标CNN, 从而使目标分类器错误分类。

定义3 攻击目标:假定CNN流量分类器为F, 网络流的灰度图像为X, 则 ()Xy=F ,y为预测标签。对抗样本advXXδ= + , 这里δ是一个微小的扰动量。为确保advX和X的变化很小, 增加约束||||pδ≤∈, 这里||||p· 为p范数。本文提出的攻击目标只要求将advX错误分类, 即:

定义4 攻击能力:攻击能力是指攻击者掌握目标CNN信息多少的程度, 分为白盒攻击和黑盒攻击[18]。白盒攻击是指攻击者几乎知道关于神经网络的所有信息, 包括训练数据、激活函数、拓扑结构等。黑盒攻击则假设攻击者无法获得已训练的神经网络内部信息, 仅能获得模型的输出, 包括标签和置信度。由于黑盒攻击不需要了解模型内部信息, 因此更符合现实中的某些场景攻击。本文假设攻击者仅需知道目标流量分类器是采用CNN模型, 因此属于黑盒攻击。

3.2 攻击方法

算法1: 网络流对抗样本攻击 输入: 网络流 1 2 F ff f 输出: 攻击用的伪造流量数据S 1: 初始化S←∅ 2: while i < N do 3: 网络流 if F∈ 转换为灰度图像 ()i X 和它 的掩模矩阵 iM 4: () (sign( (, ,)))⊙={ , ,..., }N X i v X y←+ ∇L ε θX M ad X i

//利用FGSM等方法生成 ()i X 的对抗样本 5: 根据掩模 iM, 提取 ()i advX 中的数据包头, 恢复为网络流 if′ 6: 根据 if′包头中的信息和篡改后的负载, 伪造数据包流S← 1 2′′ ′∪… { , , , }pp p k 7: end while

在上述威胁模型的假设下, 本文采用如下的攻击方法: 首先对采集到的流量数据, 预处理为灰度图像, 建立与目标模型同分布的本地训练集。然后利用D训练本地代理CNN, 获得分类器~F, 模拟目标流量分类器F。在本地代理CNN上生成对抗样本。最后将对抗样本转回网络流量if′, 这是因为正常的网络流图像已经变为, 且两者之间的变化非常微小, 使目标CNN产生错误分类的预测。根据网络流if′再伪造出数据包流 {p1′ ,… ,pk′}, 向目标CNN模型重放。

由于CNN的特征抽取主要针对数据包的内容负载, 因此我们仅对数据包内容进行扰动, 不对数据包头的控制信息改变, 这样有利于逆向构建攻击流量。为了确保数据包头不被改变, 我们引入掩模(mask)矩阵, 它是一个与输入图像同样大小的0～1矩阵。对应原图像数据包头区域为0, 数据区域内容为1:

这里 (,)Xij对应网络流中的某个字节。公式(4)根据数据包头部的控制信息, 构建出每个数据流图像的掩模矩阵。由于CNN反向传播采用的是动态规划策略, 无法只对X的某些分量求梯度, 因此我们利用FGSM[19]等方法得到X的对抗样本advX, 再利用掩模矩阵获得最后的对抗样本:

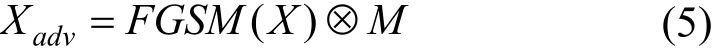
这里假设用FGSM[12]方法生成对抗样本, ⊗表示Ha-damard乘积。攻击方法如算法1所示, 第4步除了可采用FGSM外, I-FGSM[24]、LL-FGSM[24]、Deep-Fool[13]、JSMA[14]和C&W[15]等方法均可用于生成图像对抗样本。

4 对抗攻击的防御

为了防御对抗样本攻击, Goodfellow等人[12]首先提出利用对抗样本来提高模型的鲁棒性。Mardry等人[21]从优化的观点出发, 认为对抗训练是一个关于鞍点的优化问题, 他们把传统的ERM训练推广到鲁棒性训练。对抗训练是将干净图像样本和生成的对抗样本作为训练数据共同参与CNN模型F的训练, 采用代价函数的最小化原理, 使得模型最终收敛时, 代价函数达到最小, 该优化问题的形式化表示如下[21]:

其中, D为数据的分布, L为代价函数,θ为模型参数。可以发现对抗训练是个鞍点优化问题, 是内部最大化和外部最小问题的组合。内部最大化问题是找到代价最大的对抗样本, 因此对抗训练需要大量的对抗样本用于训练, 而生成对抗样本占据了对抗训练的大部分时间[17]。对于网络流量这种大规模数据, 对抗训练的时间复杂度非常高。

4.1 批次对抗训练

算法2: 批次对抗训练 输入: 训练集D; 学习率 =0.01γ 输出: 对抗训练后的模型 ()F badvθ i＜ do 2: 选取批次训练数据 iD D∈ 3: () () ()(, , )1: while epochs g i i i δ θδ←∇ +L δ X y //计算损失函数对样本的梯度 4: () () ()(, , )g i ←∇L , ()i i i θ θX y θ gθ ← adv() ()∇L //计算损失函数对模型参数的梯度 5: () ()( ), 1, ,θ θX y i i adv (, , )i i = … //取k个训练数据生成对抗样本 X Gg i k adv ←θadv(∑ ∑g() ()i i +λ g θ)~L //计算总代价梯度 7: 1 ()6: ∇ ← - +λ θadv iCLEAN jADV ∈∈θ() ( )θ m k k+← +∇ ~L //更新模型参数 8: end while θ θγθ i i θ

为了提高对抗训练的速度, 我们将以往单个样本的在线对抗训练改进为按批次进行训练, 同时利用反向传播过程中的误差传递, 同时完成更新模型参数和对抗样本生成这两个步骤。假设批次训练的数据为, 我们假设函数G(·)为对抗样本生成函数, 选取k个训练数据生成对抗样本θ为当前模型的参数。更新当前批的训练数据为, 批次对抗训练的代价函数为:

其中, (,,)XyθL 是正常样本的代价函数, L(θ,Xadv,y)是对抗样本的代价函数,m是批次对抗训练的总样本数, 参数λ是控制对抗样本的比例。

我们分析了以往在线对抗训练算法, 发现生成对抗样本和更新模型参数是分开进行的, 这会带来两次反向传播求去梯度的问题。通过推导, 可以发现损失函数L对模型参数θ的梯度和对扰动δ的梯度, 在反向传播过程中都可利用误差σ=∂L /∂S计算, 这里S表示神经元的输入。为此, 我们在一次反向传播过程中同时计算出它们梯度, 大大加快计算速度。

4.2 增强对抗训练

算法3: 增强对抗训练 输入: 基准模型 ()θF ;训练集D; 预训练模型 1{ ()}N i iθ =F ; =0.5t 输出: 对抗训练后的模型 Fs adv(θ) k＜ do 2: 选取批次训练数据 iD D∈ 1: while epochs 3: for j X in kD do ∑ L L 4: if tψ≤ then 5: （ ）1{ } { , }4: ψ←log( exp( ( , )))CS∇ ∇1＜＜＜X a X b abN j X GX B =adv ←j N i i //每个预训练模型均生成对抗样本 6: else tψ＞ then （ ）j j ∈ … //随机选一个预训练模型生成对抗样本 7: end if 8: { }j{ } {1, ,}X GXB i N adv ←, ，i′← ∪ //更新当前批次训练数据9: 根据式(7)计算总代价 ()θ~L 10: 1 ()D D X k k adv k+← +∇ ~L //更新模型参数 11: end for 12: end while θ θγ θ k θ

批次对抗训练可以较好的防御白盒攻击下的特定攻击, 但攻击者仍可采用黑盒攻击, 在这个样本点附近随机跳跃, 再进行单步攻击CNN[12]。为了防御这类黑盒攻击, 我们进一步提出新的训练方法——增强对抗训练。主要思想是增加对抗样本的多样性, 为此提出流量对抗样本的差异性筛选方法。实验证明, 增强对抗训练不仅可以防御针对流量分类器的白盒攻击, 而且可以防御黑盒攻击。

假设有两个预训练模型1()XF 和2()XF 。∇XL1(θ1,X,y)和 ∇XL2(θ1,X,y)分别表示两个模型的代价函数对样本X的梯度, 是该样本的最佳扰动方向, 沿此方向添加扰动可最大限度的增大CNN的代价函数。如果 ∇XL1(θ1,X,y)和 ∇XL2(θ1,X,y)的方向一致, 或近似一致, 那么意味着沿此梯度方向获得的对抗样本advX既能攻击模型1()XF 上, 也能攻击2()XF 。从防御角度看, 使用1()XF 生成的对抗样本进行对抗训练, 就能防御2()XF 生成的对抗样本。如果 ∇XL1(θ1,X,y)和 ∇XL2(θ1,X,y)的方向不一致, 那么样本X就需要在1()XF 和2()XF 上分别生成对抗样本进行对抗训练。因此, 样本X是否需要在每个模型上生成对抗样本, 取决于预训练模型之间的梯度对齐程度。我们使用余弦相似度(CS)来量化这种对齐程度:

这里, ＜∇XL1,∇XL2＞表示两个梯度向量的内积。当CS较小时, 表明样本X在两个模型上的差异性较低, 需要两个模型都生成对抗样本进行训练。反之, 只需用其中一个模型生成对抗样本进行训练。

为了度量样本在N个预模型之间的差异性, 我们把余弦相似度推广到N个模型的情形, 取其最大值:

由于ψ是非光滑函数, 不宜采用梯度下降等优化方法, 进一步用LogSumExp函数来近似ψ:

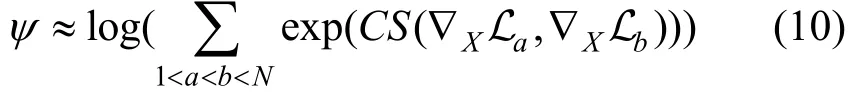
当tψ≤时, 对于每个预训练模型, 都需用X生成对抗样本参与对抗训练, 反之选择其中一个预训练模型生成对抗样本训练, 本文设置 0.5t= 。

5 实验分析

5.1 网络流量数据集

本文采用的实验环境: 操作系统Ubuntu16, GPU NVIDIA TITAN 2080, tensorflow-gpu 1.8.2, numpy 1.16.1。网络流量集为USTC-TFC2016[9], 该数据集以Pcap文件格式存储, 包含了两部分, 第一部分是从2011年到2015年收集的10种公开的恶意网络流量[25], 第二部分是使用网络模拟设备IXIA BA[26]采集包含10种正常网络流量。本文使用第二部分的正常网络流量。网络流数据是使用USTC-TK2016[9]将原始流量按图1的处理流程得到的175,178网络流记录。各个流量类的网络流可视化后的部分实例如图2所示。从可视化结果中不难发现, 不同网络应用类别的灰度图像具有明显的可区分度, 且在同一类别中具有一致性。我们将生成的灰度图像集合划分为训练集和测试集, 其中测试集和训练集的比例是1∶9。

图2 网络流转为灰度图像示例 Figure 2 Example of network traffic converted to grayscale image

5.2 CNN参数设置

本文实验用的CNN模型为LeNet-5, 激活函数为ReLU函数, 池化层均采用最大池化方法, 池化和卷积均使用全0填充以避免图像边缘信息丢失太快, 具体模型结构如表1所示。我们把目标模型标记为FA。同时为了进行增强对抗训练, 选择4个预训练模型(FB,FC,FD,FE)用于生成差异性对抗样本。除训练过程的超参数不同外, 4个模型的结构与目标模型 FA相同, 具体设置如表2所示。

表1 实验模型LeNet-5的结构 Table 1 The structure of the experimental model Le-Net-5

表2 预训练模型的超参数与准确率 Table 2 Hyperparameter and accuracy of pre-trained models

5.3 对抗样本攻击效果

为了区分模型自身分类错误的样本, 实验只使用目标模型分类正确的样本用于生成对抗样本。生成的流量对抗样本如图3所示。FGSM以及变种生成的对抗样本在模型 FA上的准确率如表3所示。可以发现, 当扰动量阈值∈增大到0.07时, 模型AF的准确率从96.15%降低到7.35%。但随着∈的继续增大,攻击成功率降低速率变得缓慢, 最后几乎趋近于0。而对于I-FGSM来说, 在迭代次数小于5时, 对抗样本在模型AF上的准确率快速下降。随着迭代次数的增加, 准确率同样下降变缓, 原因是固定长度的扰动步长会导致在局部最小值点附近震荡, 收敛变慢。与FGSM和I-FGSM相比, LL-FGSM对流量分类器表现出更好的攻击稳定性。

图3 FGSM、I-FGSM和LL-FGSM生成流量对抗样本的灰度图像 Figure 3 FGSM, I-FGSM and LL-FGSM generate grayscale images of traffic adversarial examples

表3 模型 AF在不同强度对抗样本攻击下的分类准确率 Table 3 Classification accuracy of model AF under different intensities of adversarial attacks

DeepFool、JSMA以及C&W生成的流量对抗样本的攻击效果如图4所示。其中C&W-2表示基于2l范数约束, C&W-inf基于l∞约束。K代表生成对抗样本的方法迭代次数。从结果中可以发现DeepFool与JSMA方法的攻击效果要好于C&W方法。

图4 模型 FA在不同类型流量对抗样本攻击下的分类准确率 Figure 4 Classification accuracy of model FAunder different types of traffic adversarial examples attack

5.4 批次对抗训练防御

为了进行实验比较, 选择模型 FA作为目标模型, 其在测试集上的准确率为96.15%, 模型 FA-oadv和FA-badv分别是模型 FA在线对抗训练后和批次对抗训练后的流量分类器, 测试集准确率分别为93.66%和92.14%。表4表示不同对抗训练方式对于FGSM生成对抗样本的防御能力。

表4 采用不同扰动阈值的FGSM对抗样本攻击对抗训练后的模型分类准确率 Table 4 Classification accuracy of FGSM adversarial examples attack adversarial training model with different perturbation thresholds (%)

对于每种攻击方法, 均采用模型 FA-oadv和FA-badv作为目标模型。从实验结果发现不管是在线对抗训练还是批次对抗训练, 都能够提高模型 FA的 鲁棒性。表5是在线对抗训练和批次对抗训练的时间复杂度对比, 可以发现, FGSM的在线对抗训练耗1.32 h, 而批次对抗训练仅需要15 min, 因此在流量分类这样的大数据环境下, 批次对抗训练具有明显的效率优势。

从图5中也可以发现, 对抗训练可以提高对于白盒攻击的鲁棒性。对于C&W攻击方法, 即使对抗样本的扰动幅度增强到约束极限, 经对抗训练后的模型 FA-oadv和FA-badv分类准确率仍保持在70%以上, 未经对抗训练的模型 FA分类准确率已下降到17%。从表5中的时间效率上看, DeepFool、JSMA和C&W生成的流量对抗样本进行批次对抗训练的平均耗时为14.3 min, 而在线对抗训练平均耗时长达1.67 h。因此, 本文提出的批次对抗训练在时间复杂度上更具较好的优势。

图5 对三种不同模型的对抗攻击效果比较, 包括未进行对抗训练的模型 FA、传统在线对抗训练后的模型FA-oadv、改进后的批次对抗训后的模型 FA -badv; (a)、(b)、(c)、(d) 分别对应四种对抗样本生成方法 Figure 5 Comparison of the performance of adversarial attacks on three different models, including model FA without adversarial training, model FA -oadv after traditional online adversarial training, and model FA -badv after improved batch adversarial training; (a), (b) , (c), (d) correspond to the four adversarial examples generation methods respectively

表5 在线对抗训练和批次对抗训练的时间对比 Table 5 Comparison of online adversarial training and batch adversarial training time

为了进一步分析对抗训练防御白盒攻击和黑盒攻击的效果, 对不同模型进行了比较实验, 结果如表6所示。其中第一行表示用于生成流量对抗样本的CNN模型, 第一列表示用于攻击的目标CNN模型。目标模型 FA和 FB经过批次对抗训练得到 FA-badv和 FB-badv。对角线为白盒攻击后的分类准确率, 其余为黑盒攻击后的分类准确率。 实验结果表明, 批次对抗训练对可以大幅提高模型对流量白盒攻击的鲁棒性。经批次对抗训练后的模型 FA-badv, 分类准确率从17.29%提高到75.37%, FB-badv从14.39%提高到81.09%。但批次对抗训练对黑盒攻击的防御效果并不显著, 未经对抗训练的模型 FA对于模型 FB生成的对抗样本准确率为26.37%, 经批次对抗训练后的模型 FA-badv反而只有19.78%。由此可见, 批对抗训练对黑盒攻击的防御能力不佳, 需要有针对黑盒攻击的防御方法。还可从表6发现, 用对抗训练后的模型 FA-badv和FB-badv来生成对抗样本, 对其他模型几乎无攻击效果, 这与Madry等人[21]的实验结果一致, 即对抗训练在增强模型的鲁棒性同时, 削弱其生成对抗样本的能力。

表6 批次对抗训练后的模型在黑盒攻击和白盒攻击下的FGSM对抗样本分类准确率比较 Table 6 Comparison of FGSM adversarial examples classification accuracy of the models after batch adversarial training under black box attack and white box attack (%)

5.5 增强对抗训练的防御效果

针对批对抗训练防御黑盒攻击的能力不足问题, 我们进一步提出增强对抗训练, 将生成对抗样本的CNN从单个变成多个, 同时通过样本的差异性筛选, 增加对抗样本的多样性, 最终实现增强防御黑盒攻击的效果。用于样本筛选的模型如表7所示, 第一行表示模型 FA, FB用于筛选出差异性对抗样本, 然后对模型 FA进行增强对抗训练得到模型 FA-sadv-1和

表7 增强对抗训练模型及对应的样本筛选模型 Table 7 Enhanced adversarial training model and corresponding example screening model

FA-sadv-2。

为了验证增强对抗训练对于黑盒攻击的防御性能, 我们进行了表8中的实验, 其中第一行中模型表示生成流量对抗样本, 第一列中的模型为受到流量对抗样本攻击的目标模型, 不同的是, 模型 FA未经过对抗训练, 模型 FA-badv经过批次对抗训练, 模型FA-sadv-1, FA-sadv-2经过增强对抗训练。我们把生成对抗样本的模型和防御模型为相同结构的情况, 成为白盒攻击/防御。生成对抗样本的模型和防御模型的结构不同, 则称之为黑盒攻击/防御。从表8的实验结果可以发现, 增强对抗训练对于白盒攻击的效果与批次对抗训练效果相当, 目标模型 FA-badv和FA-sadv-1对于模型 FA生成的对抗样本攻击的准确率 基本接近, 分别为75.37%和73.25%。但是增强对抗训练后的模型在黑盒攻击中具有更好的鲁棒性, 如目标模型 FA-sadv-1和FA-sadv-2对于模型 FB生成的流量对抗样本, 准确率分别为68.39%和62.17%, 远高于模型19.78%的准确率。由此可见相比较批次对抗训练, 增强对抗训练对于黑盒攻击的防御效果更好。

表8 增强对抗训练后的模型在黑盒攻击和白盒攻击下的FGSM对抗样本分类准确率比较 Table 8 Comparison of FGSM adversarial examples classification accuracy of the models after enhanced adversarial training under black-box and white-box attacks (%)

此外, 我们将本文提出的增强对抗训练防御方法与一些经典有效的防御方法, 进行了防御黑盒攻击的实验对比, 实验结果如表9所示。可以发现, 在黑盒攻击模型下, 相比较防御蒸馏[19]、对抗样本检测[20]方法, 本文提出的增强对抗具有更强的防御对抗样本的能力, 如防御蒸馏和对抗样本检测对于FGSM对抗样本的分类准确率为49.72%和54.32%, 而增强对抗训练的分类准确率可以达到75.37%远高于防御蒸馏和对抗样本检测。

表9 黑盒攻击下, 增强对抗训练与其它防御方法对抗样本分类准确率对比 Table 9 Comparison of accuracy of adversarial examples classification between enhanced adversarial training and other defense methods under black box attack (%)

6 结论

本文提出了针对CNN流量分类器的对抗样本攻击方法, 并在真实流量数据集上验证了这种攻击的有效性。为了防御这类对抗样本的攻击, 我们提出了批次对抗训练方法, 主要防御对抗样本的白盒攻击; 提出增强对抗训练方法, 主要防御对抗样本的黑盒攻击。实验结果表明, 针对白盒攻击, 批次对抗训练可使目标模型的分类准确率从17.29%提高到75.37%; 针对黑盒攻击, 增强对抗训练可使对抗样本的分类准确率从26.37%提高到68.39%。本文提出的对抗训练方法可有效的增强CNN流量分类器的防御能力。对抗训练是一种防御对抗样本的较好方法, 但是目前仍缺乏对CNN脆弱性机理有深刻认识, 因此无法进一步提升对抗训练的效果, 我们的下一步工作将从理论上深入研究其作用机理。