一类考虑未就诊患者带分布时滞的SIS模型分析
齐龙兴,程光一,包云婷
(安徽大学 数学科学学院,合肥 230061)
2020年全球暴发了新冠疫情,引起了人们对疾病传播情况的重视,已有大量学者对新冠肺炎进行了研究[1-2].除新冠肺炎外,对人类生命造成威胁的还有SARS,疟疾,AIDS,H7N9等传染性较强的流行病[3-4].一些流行病在发病初期的症状类似于普通流感,未引起人类重视,并不去医院就诊,直到症状出现严重不适时才去医院就诊,而此阶段已出现传染性[5].除此之外,当易感者被传染后,要经历一段时间才产生传染性,传染病的时滞一般在2~14天,如霍乱在2天左右,新冠病毒的时滞在14天内[7-8].这些都说明疾病的感染会出现滞后性,并且在疾病传染期间是连续的[6],因此分布时滞更能反映其滞后性.
当前,已有很多学者在研究流行病时采用分布时滞[1,7-13],严阅等[1]针对新冠肺炎疫情建立了具有分布时滞的IJGR模型,采用数值分析方法对所建分布时滞模型进行模拟,预测疫情传播趋势.ZHANG等[9]考虑了具有分布时滞的非自治疟疾传播模型,对其持久性、灭绝性以及全局渐近稳定性进行了理论分析,最后进行数值模拟分析理论结果.ZOU等[10]考虑了具有分布时滞和脉冲控制策略的生态流行病模型,对系统进行了理论分析,并通过数值模拟发现理论结果中的周期解是由脉冲效应和时间延迟引起的.YIN等[11]使用重合度理论的连续定理,得到具有反馈调节和分布时滞的单物种模型正周期解存在性的判据.ZHANG等[15]在Edoardo Beretta的具有分布时滞的SIR模型[12-14]上,考虑了具有分布时滞的SIRS模型,主要进行理论分析,得到基本再生数R0,并且当R0>1时,疾病持久.通过Lyapunov函数得到无病平衡点的稳定性以及地方病平衡点局部稳定的充分条件.但是他们都没有考虑未就诊患者以及未就诊患者在疾病传播中的时滞性.
在疾病传播中,还有学者考虑多种类型的感染人群,例如CAI等[16]考虑了包含有症状感染者与无症状感染者的模型,建立了艾滋病传染病模型,对其进行理论分析,其对应的离散时滞模型出现了霍普夫分支.文献[17]针对新冠肺炎也考虑了无症状感染者对疾病传播的影响,得到了解无症状传播的时间过程对于评估这种传播途径的重要性和疾病动力学非常重要.但是未就诊患者代表已经患病但未去医院就诊的人群,此类人群中有因为无明显症状不知患病的,也有症状轻微不愿去医院就诊的.因此,未就诊患者人群不仅包括无症状感染者,也包括有症状感染者.值得注意的是,很多疾病的未就诊患者与就诊患者均有传染性,然而未就诊人群在总人群中的具体数量[5]是无法准确得知的.因此,未就诊患者的传染性经常容易被忽略,其发病的滞后性更容易被忽略.所以,考虑未就诊患者的传染性及其发病的滞后性对疾病传播的影响至关重要.BAO等[18]考虑了未就诊人群在呼吸道系统传播疾病的影响,建立含未就诊人群的SIS模型,并结合合肥市呼吸道系统就诊数据进行数值模拟,得到增强免疫力,就可使就诊病人下降,最终总病人数下降.之前工作未考虑未就诊病人的滞后性,因此本文主要考虑未就诊患者对易感者的传染,并加入分布时滞,建立含分布时滞的SIS模型.
1模型建立与平衡点存在性
1.1 模 型
通过考虑传染性疾病的未就诊人群以及疾病的分布时滞,建立如下含分布时滞的SIS模型:
(1)
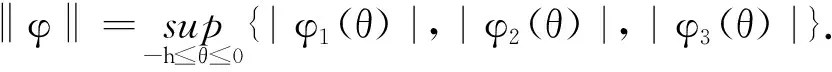
1.2 平衡点的存在性


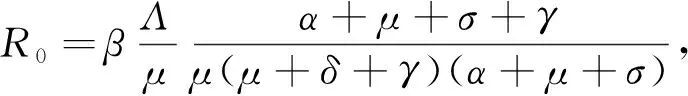
根据生物意义知R0为系统的基本再生数,
其中R0a表示每个未就诊人群感染期间新产生的病人数,R0s表示每个未就诊人群就诊后在其感染期间新产生的病人数.因此R0表示患者人群在其感染期间新产生的第2代总病人数.
2 持久性
在系统(1)中,Ia(t)和Is(t)均表示患者,在此令I(t)=Ia(t)+Is(t),则系统(1)化为
(2)
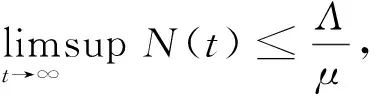
证明由于系统(2)在不变集上是连续的且在C上是局部Lipschitz的,其初始状态下的解在[0,b)(0≤b≤+∞)上存在且唯一.断言对∀t∈[0,b),S(t)>0.为证明断言正确,考虑其否定情况,即存在一个t1∈[0,b),使得S(t1)=0以及S′(t1)≤0,当t∈[0,t1),S(t)>0.下证在t∈[0,t1)时,必有I(t)>0,否则存在一个t2∈(0,t1),使得I(t2)=0,当t∈[0,t2),I(t)>0.
由系统(2)第2个式子得到

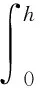
将其在[0,t2)上积分后,有
与I(t2)=0矛盾.因此在t∈[0,t1)上,I(t)>0.
下面证明∀t∈[0,b),S(t)>0的否定情况不成立.由系统(2)第1个式子得到
S′(t1)≥Λ+σIa(t1)+σIs(t1)≥Λ+kI(t1)>0,
其中k=min{δ,σ},与S′(t1)≤0矛盾.因此S(t)>0在[0,b)(0≤b≤+∞)上成立.
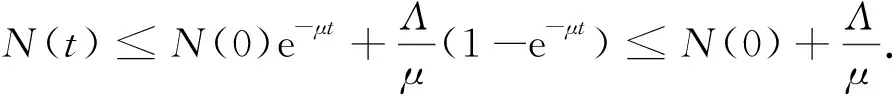

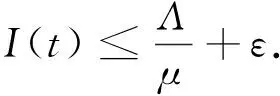

显然R0-R*恒大于0,因此R0>R*恒成立.

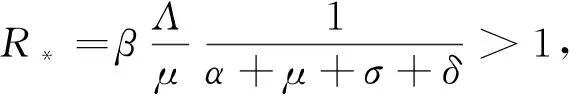
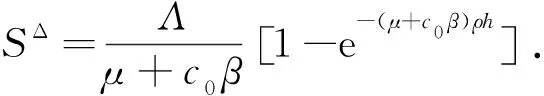
V(t)沿系统(2)的导数为

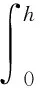
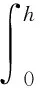
现断言在所有的t≥t1≥ρh上I(t)≤c0是不可能的.考虑相反情况,则当t≥t1+h时,

上式在[t1+h,t]上积分,得
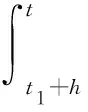
所以当t>t1+h+ρh时,
(3)
通过以上不等式可得,当t>2ρh+h时,

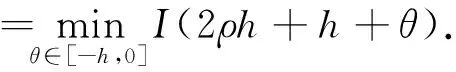
另一方面,由系统(2)第2个方程可以得到,当t=2ρh+h+T,

与I′(2ρh+h+T)≤0矛盾.因此,对所有的t>2ρh+h,有I(t)≥i.
进而,当t>2ρh+2h,有V′(t)>[βS(t)-(α+μ+σ+δ)]i,所以t→+∞时,V(t)→+∞,与V(t)有界矛盾.因此断言正确.
现在I(t)有两种可能:对于足够大的t,I(t)≥c0或者I(t)在c0处摆动.
现证当t足够大,I(t)≥c0e-(α+μ+σ+δ)(h+ρh).若I(t)≥c0,则I(t)≥c0e-(α+μ+σ+δ)(h+ρh)一定成立.因此,现考虑I(t)在c0处摆动的情况,任取足够大的t1,t2,满足I(t1)=0,I(t2)=c0,且当t∈(t1,t2)时,I(t)≤c0.若t2-t1≤h+ρh,由于I′(t)≥-(α+μ+σ+δ)I(t),则通过积分计算,可得t∈[t1,t2],I(t)≥c0e-(α+μ+σ+δ)(h+ρh).若t2-t1>h+ρh,则当t∈[t1,t1+h+ρh]时I(t)≥c0e-(α+μ+σ+δ)(h+ρh).现证明在[t1+h+ρh,t2]上也成立.若在t∈[t1+h+ρh,t2]时不成立,则存在T*>0,使得当t∈[t1,t1+h+ρh+T*]时,有I(t)≥c0e-(α+μ+σ+δ)(h+ρh),I(t1+h+ρh+T*)=c0e-(α+μ+σ+δ)(h+ρh)且I′(t1+h+ρh+T*)≤0.由系统(2)以及(3)式得:

[βSΔ-(α+μ+σ+δ)]c0e-(α+μ+σ+δ)(h+ρh)>0.
因此与I′(t1+h+ρh+T*)≤0产生矛盾.所以I(t)≥c0e-(α+μ+σ+δ)(h+ρh)在t∈[t1,t2]均成立.
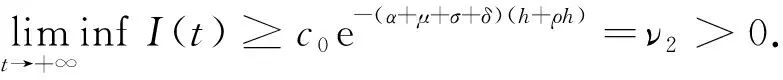
通过定理1~3得到系统(2)的解是持久的.
3 平衡点的稳定性
3.1 无病平衡点的稳定性
定理4当R0<1时,无病平衡点E0全局渐近稳定;当R0>1时,E0不稳定.
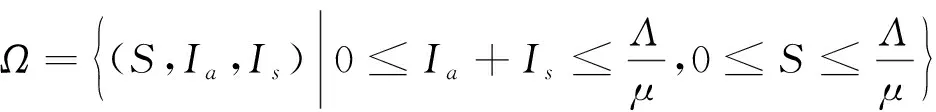


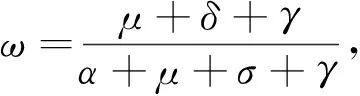
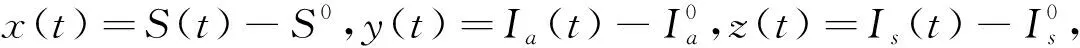
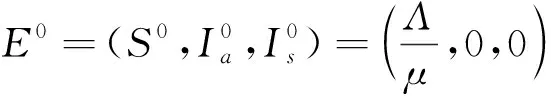
令
则f(λ)是关于λ的开口向上的二次函数.在τ>0的条件下,当R0>1时,有
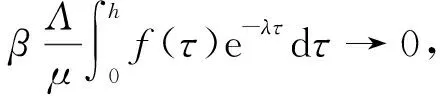
f(λ)→λ2+(μ+δ+γ+α+μ+σ)λ+(μ+δ+γ)(α+μ+σ)→+∞.
所以,必存在一个实部为正的λ+,使得f(λ+)=0,因此E0不稳定.
3.2 地方病平衡点的局部稳定性
引理1[19]若存在非负连续向量函数ω1(·),ω2(·),满足当且仅当x=0,ωi(x)=0,且当x→+∞,ω1(x)→+∞,V∶C([-τ,0],Rn)→R是连续微分向量函数,其在系统(1)的解满足:
V(φ)≥ω1(φ(0)),V′(φ)≤-ω2(|φ(0)|),
则系统的解是渐近稳定的.


取其线性部分:
考虑Lyapunov函数
其中ω1>0,ω3>0.则V(ut)沿上述线性系统求导,得到

情形1 若α=0,则
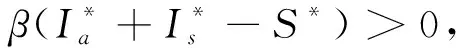
由引理1可知E*局部渐近稳定.
情形2 若α≠0,则
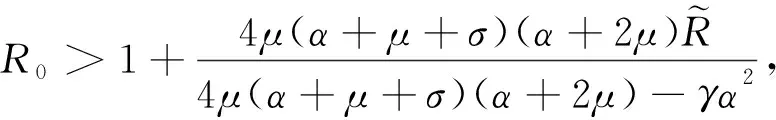
若上式为负定二次型,则必须满足
[ω1(α+2μ)]2-4μω1[ω1(α+μ)+ω3(α+μ+σ)]<0,
即[ω1(α+2μ)]2<4μω1[ω1(α+μ)+ω3(α+μ+σ)],则ω1α2<4μω3(α+μ+σ).
进而可得:

4 数值模拟
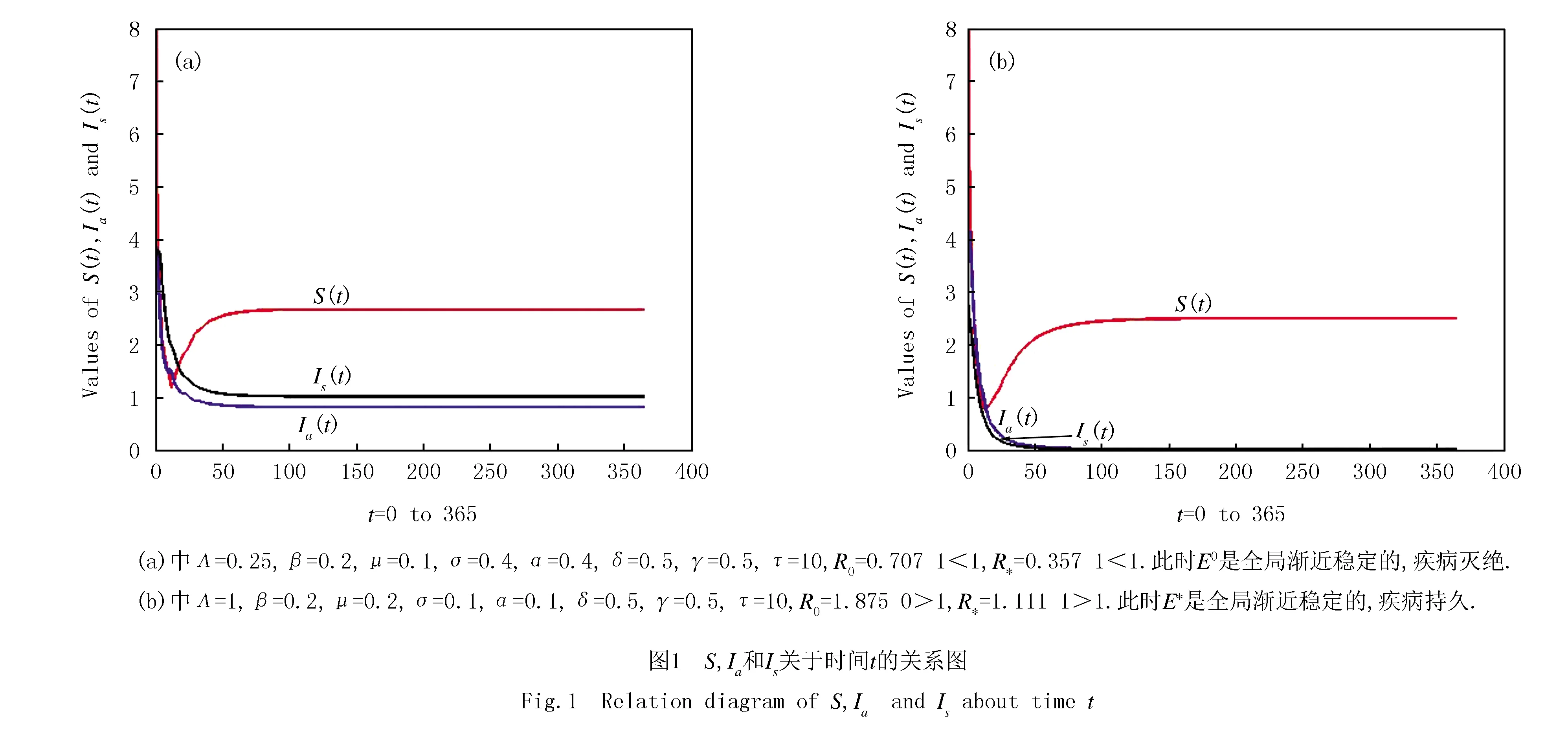
为验证系统的稳定性情况,针对系统(1)进行数值模拟,见图1.
下面考虑变化时滞后,观察时滞对系统动力学的影响.
从图2中可以看出在R0>1时,时滞τ越小,未就诊病人数达到的峰值越大;反之,未就诊病人数达到的峰值越小.因此从被感染到具有感染力的时间的长短会影响病人数到达的峰值高度.
5 讨 论

为观察时滞对系统的影响,以及各类人群的发展情况,对其进行了数值模拟.结果显示,当R0<1时,无病平衡点E0渐近稳定,疾病灭绝;当R0>1时,地方病平衡点E*渐近稳定,疾病持久.在理论证明中,定理2中的附加条件为E*局部稳定的充分条件,因此当且仅当R0>1时,地方病平衡点的渐近稳定性的理论还未完善.未来将在此理论基础上继续研究,进行完善.