巧设计 激思维 提能力

蔡婷洁

在传统的小学数学课堂中，对学生而言，时常是在被动学习的状态中，师生之间维持着一种“教师讲，学生听”的关系，这样的课堂教学使学生缺乏问题意识，也不具备提出问题和解决问题的能力；对教师而言，在我们教学时往往没有有效解决这个难点的教学策略，而使解决问题的教学陷入困境。例如五年级数学中的“追及问题”一直是老师和学生心中的一块硬骨头，老师讲得口干舌燥、声嘶力竭，学生依然不明白、不理解问题转化和解决的过程，学生面对题目中涉及的多个速度、路程以及时间会眼花缭乱、思路混乱。

《课程标准》中的“课程目标”提出：要初步学会从数学的角度提出问题、理解问题，并能综合运用所学的知识和技能解决问题，发展应用意识；形成解决问题的一些基本策略，体验解决问题策略的多样性，发展实践能力与创新精神。

因此，在新课改的背景下，要想培养学生解决问题的能力，就必须要针对这一问题整合单元教材资源，制定有效的、可操作的教学策略，只有这样才能够有效地培养学生的问题意识，使学生更好地掌握数学知识，发展数学思维，培养核心素养，实现深度学习。

（一）学生现场演绎，寻找关键信息

“追及问题”的特征是两个物体一前一后、一慢一快同向运动，快者逐渐追上或超过慢者。沪教版小学数学中把“追及问题”安排在五年级第二学期第三单元“简易方程”中列方程解决问题。

在第一次教学“追及问题”时，我直接搬用了教材中的情境“一辆客车和一辆汽车先后从上海出发去南京，客车先行50千米后轿车出发，客车平均每小时行80千米，轿车平均每小时行100千米，轿车几小时后追上客车？”作为教师，我只是简单地教教材，而不是用心地用教材教；作为学生，这样的情境距离他们实际生活较远，不容易被理解，也无法激发学生的学习兴趣和思维。整节课下来，我教得辛苦、学生学得无趣，课堂氛围死气沉沉、毫无生机。

于是，我仔细分析教材、转变角色、静心思考，我发现小学数学学科的教学主要依托方式是题目，学生在看到一条由文字组成的题目时，大多数的学生都是从表面解题，不会去思考问题中的重要概念、寻找关键信息。因此，我们老师需要在教学时把此类枯燥的、较难理解的题目注入新的活力和生命，以一种直观的、学生容易理解和喜爱的方式呈现。

在第二次教学时，我借助例题、创设贴合学生生活的情境：小丁丁早上出门上学，他平均每分钟走75米，他走出500米后妈妈发现他忘带作业袋，立即骑自行车以每分钟200米的速度追赶，几分钟后妈妈能追上小丁丁？

【教学回顾】

师：这样的场景是不是也发生在你的身边？

生：有的，我还忘记过书包。

（底下同学哄堂大笑。）

师：现在我邀请两位同学来扮演小丁丁和他的妈妈，并把这一过程表演出来。

（孩子们一边笑着一边举手，他们迫不及待、跃跃欲试。）

生1：我想演小丁丁。

生2：那我演小丁丁的妈妈。

师：那就请两位小演员就位，开始你们的表演。

【学生现场演绎后】

师：你从刚才的情境表演中发现了哪些重要的、关键的信息？

生：我看出來是小丁丁先走，妈妈后来才开始走的。

师：你观察得非常仔细，这一发现很重要，那为什么小丁丁要先走，妈妈后走？而不像“相遇问题”中同时出发呢？

生：因为小丁丁速度慢，妈妈速度快，慢的人先走一段路程，快的人才会追上他。

生：如果同时出发一起走的话，那快的人就会一直在前面，慢的人一直在后面，就不会追上。

师：给他们送上热烈的掌声，分析得十分到位、清晰。所以在追及问题中，速度慢的那一方会先行一段距离，然后速度快的再出发追赶。

师：谁还找到了其他重要信息？

生：我发现妈妈用的时间就是小丁丁后面的时间，是一样的。

师：我听明白你的意思了，发现了又一个“追及问题”中的关键点，大家听懂了吗？

生：妈妈追上小丁丁用的时间和小丁丁后面用的时间是相同的。

师：除了妈妈追上小丁丁用的时间和小丁丁第二段路程用的时间相同，还有其他相等的数量吗？

生：小丁丁走的所有路程和妈妈骑车的路程是相等的，都是从家到妈妈追上小丁丁的那段距离。

师：你们真的很棒！从刚才两位同学非常生动、直观的演绎中，我们发现了很多重要信息。这对我们的解题非常有帮助。

这样的情境学生比较熟悉，甚至亲身经历过，他们有较强的认同感。青浦实验的“情意原理”提到：把问题作为教学的出发点。教师应该积极创设情境，如与学生一起对某些问题进行考察，以激发学生的求知欲和思维的积极性。二期课改也提出“要重视学生的学习经历和经验，强调课程设计从学生的角度出发，要与学生的经历经验相联系，确立学生在学习中的主体地位。”

的确，学生在进入课堂学习时并非是一张白纸，他们的生活经验和已有的数学基础都会在学习过程中起作用。因此，我们在教学中首先要考虑教学内容与学生实际生活之间的联系，考虑到影响学生抽象出数学概念的因素，然后制定相应的教学策略，创设符合学生年龄特点和生活实际的问题情境，引导学生在生活经验的基础上发掘概念的数学本质属性，寻找解题的关键信息。

（二）借助数形结合，厘清数量关系

数学学习过程不仅是一个接受知识、积累知识的过程，还是一个探索知识、创造知识的过程。数形结合思想是数学中最重要、最基本的思想方法之一，是解决许多数学问题的有效思想。让学生学会构建模型来直观描述数学问题，以形助数、以数辅形，不仅可以发展学生的思维能力，还可以培养学生解决问题的能力。

在学生理解追及概念、找到关键信息后，以“相遇问题”线段图为基础，我让学生自己独立思考该如何画出“追及问题”的线段图然后全班交流。

【教学回顾】

师：哪位同学能来交流一下你的线段图是怎么画的？

生：我画了两条线段，一条表示小丁丁，一条表示妈妈。

师：为什么不像“相遇问题”那样画一条呢？

生：两个人都是从家出发，如果是一条，那就没办法清楚地看出哪里是小丁丁走的，哪里是妈妈走的。

师：你解释得很有道理，因为两个人都从同一个地点出发，为了看得清楚，画两条线段分别表示小丁丁和妈妈。还有呢？

生：这两条线段图要头和头对齐，尾和尾对齐。

师：头、尾分别对齐想要说明什么？

生：头就代表小丁丁家，他们都是从家里出发的，出发点一样，所以头对齐。

生：尾对齐是因为妈妈追上小丁丁了，所以尾也要对齐的。

师：老师真的对你们刮目相看，分析得十分透彻。还有什么补充的吗？

生：要两条线段图上分别标上他们各自的速度。

师：没错，这一点也很重要。还有吗？小丁丁的线段图我们可以画得再细致一些。

生：我们可以把小丁丁的线段图分成两段，一段是他先走的500米，一段是他后来走的。

师：在同学们的头脑风暴下，我们完整地画出了“追及问题”的线段图，而且大家都说得有理有据。从图上，你们找到这题的数量关系了吗？

生：图上可以看出数量关系是小丁丁先走的500米加上他走的第二段路等于妈妈骑车行的路程。

师：你的数量关系讲得非常到位。借助线段图，我们可以清晰地看出数量关系并列出方程。

“追及问题”是小学数学的重、难板块，而且它的问题文字通常很长，学生理解起来非常困难，无形中增加了学生的逃避心理，降低了学生的学习动力。借助数形结合，使学生能把复杂的问题简单化，把抽象的问题具体化，为学生分析数量关系与解决问题之间架起一座桥梁。

作为教师，我们要重视对学生学习方法的指导，同时也需要给孩子们之间架起桥梁，既让他们有独立思考的空间，又有相互交流、分享的平台；既给有困难的学生解题的台阶，又让优等生有发挥的机会。

（三）善用变式练习，提升思维能力

思维是创新的基础，数学教学中变式练习是发散学生思维、提升学生思维能力的重要方式和途径。在“追及问题”中，教师可以改变问题的条件或问题，循序渐进、有层次和梯度地将原有问题转变为新的问题，由浅至深，培养学生思维的灵活性、发散性和创造性。

我把单元教学中“追及问题”的例2“一辆客车和一辆轿车从上海出发开往宁波，轿车比客车迟开0.2小时，客车平均每小时行92千米，轿车平均每小时行108千米，轿车开出多少小时候追上客车？”作为变式题，一方面我非常想检测一下改进教学后的教学效果，另一方面也想看看孩子们会不会灵活应用。

【教学回顾】

师：哪位同学能来分析一下这道题目和例题的异同点？

生：不一样的地方是例题直接告诉我们了小丁丁先走500米，而这道题目中没有直接告诉我们，是要自己求的。

师：那这题中是哪辆车先行的呢？又先行了多少呢？

生：它说轿车比客车迟开，反过来也就是客车比轿车先开，所以是客车先开。

生：客车先开的路程可以用它的速度乘以时间来求，就是92×0.2=18.4（千米）。

师：通过这几位同学的分析，我们发现是客车先行，可以用客车的速度乘以先行的时间来计算第一段路程。这是大家找到的不同点，那有没有相同的地方呢？

生：这两道题目都是追及问题，所以数量关系是和例题差不多的，客车先行的路程加第二段路程等于轿车行的路程。

师：通过大家的努力，我们发现了两道题目的区别，也找到了它们在数量关系上的共通点。

师：我现在想告诉你们，这道题目实际上是后面一个“列方程解应用题”中的例题，有没有让你们觉得自己真的很棒？

（孩子们有的说着“真的吗？”有的面露做出题目的那种满足感、成就感，有的同桌相互默默击掌。）

教师要认真钻研教材，深入分析，从学生的实际出发进行设计，借助变式练习，深化学生的理解，让学生转换思考角度，扩展解题思路，提升学生思维能力、探索能力和应变能力，发展学生的创新素质。

我想教与学的魅力大概就是如此，当老师相信她的学生能行并放手让他们做，当学生相信自己能行并努力尝试，每一个孩子都是学习的潜力者，为教学增添别样的光彩。

（一）教师方面

本节课我遵循学生的知识基础和认知规律，通过创设学生喜闻乐见、身边常见的教学情境，引导学生寻找、理解题目中的显性条件、隐性条件、数量关系等，借助线段图的数形结合使复杂的问题变得直观、简洁，并充分相信学生，通过变式练习检测教学质效，让学生真正掌握所学的数学知识。

（二）学生方面

课堂上学生亲身演绎教学情境，结合题目和直观表演，认真寻找各类数学信息，并在交流中勇敢表达自己的想法。在“相遇问题”画线段图的基础上，学生独立尝试、不断调整，借助同伴的力量互相完善线段图。同时在变式练习中学会迁移、触类旁通。学生学习兴趣高涨、各种能力得到锻炼，课堂氛围融洽。

（三）练习达成度

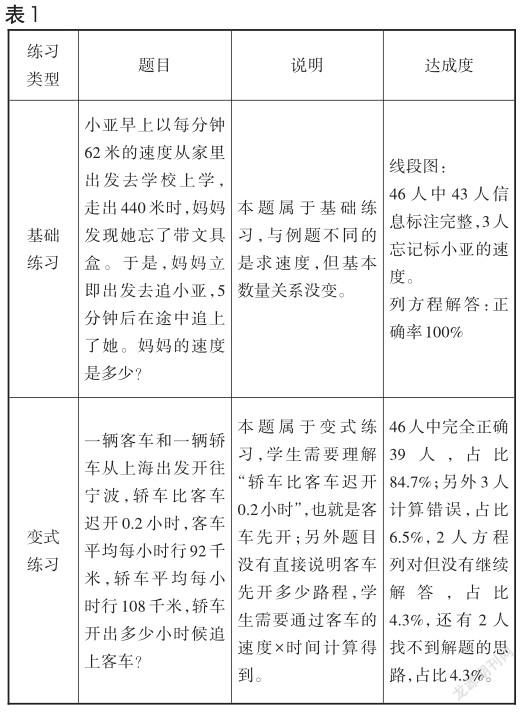
（一）基于情境，逐层深入

结合小学生的年龄和身心发展特点及学生的学习基础，在感知问题的情境中学会分析，感受已知量、未知量以及数量关系之间的逻辑联系，并逐层深入，搭建好交流平台，让学生在独立思考和全班交流中完善信息。

（二）数形结合，激发思维

运用画线段图的方式，通过直观形象的呈现，尝试解决问题，让学生认识问题的始末，再揭示问题的本质。数形结合之美在于通过直观分析获得对数学本质的认识与理解。因此，在数学教学过程中，教师应注重对学生学习方法的指导，只有这样才能真正做到“以不变应万变”。学习掌握和灵活运用这些数学思想方法，对学生解题能力的培养有重大作用和意义。

（三）学会迁移，提升能力

从简单的问题解决入手，逐步提高难度，让学生感受解决问题策略的形成过程，从而培养学生的应用能力，这是应用题教学的基本要求，也是幫助学生养成思考习惯以及解题思路，促进学生思维发展的必由之路。

作为教师，我们要增强学生学习过程的趣味性，消除学生的紧张感，同时给学生提供充足的自主学习空间，使学生不断深入探究，并提供平台进行有效的合作学习，促进学生之间的交流讨论，提高学生思辨能力，促进学生数学能力的发展，实现“让不同的学生在数学学习上得到不同的发展”目标。